Wiggle Subsequence Solution In C++/Java/Python/JS
Problem Description
A wiggle sequence is a sequence where the differences between successive numbers strictly alternate between positive and negative. The first difference (if one exists) may be either positive or negative. A sequence with one element and a sequence with two non-equal elements are trivially wiggle sequences.
For example, [1, 7, 4, 9, 2, 5] is a wiggle sequence because the differences (6, -3, 5, -7, 3) alternate between positive and negative.
In contrast, [1, 4, 7, 2, 5] and [1, 7, 4, 5, 5] are not wiggle sequences. The first is not because its first two differences are positive, and the second is not because its last difference is zero.
A subsequence is obtained by deleting some elements (possibly zero) from the original sequence, leaving the remaining elements in their original order.
Given an integer array nums, return the length of the longest wiggle subsequence of nums.
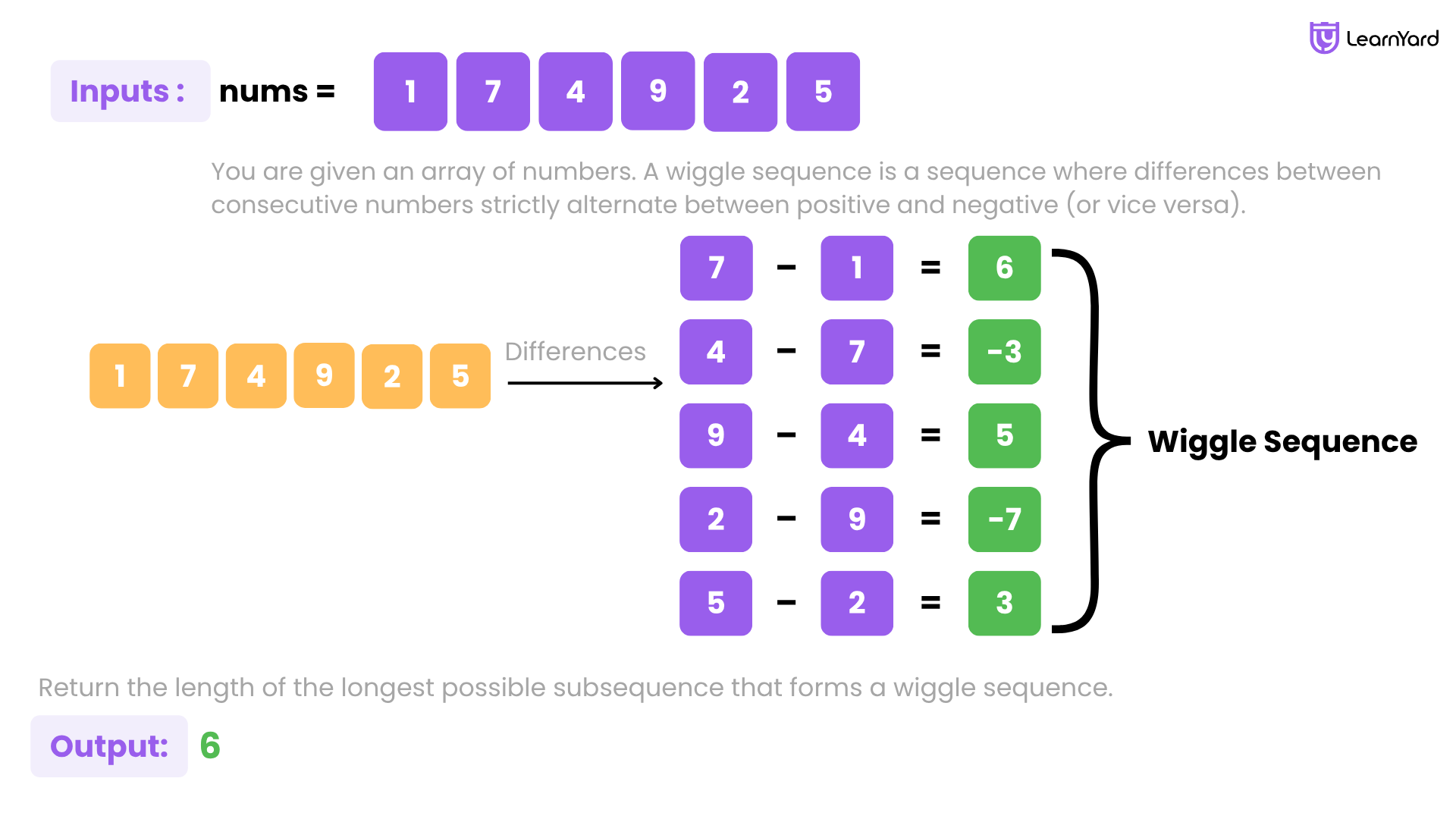
Example
Input: nums = [1,7,4,9,2,5]
Output: 6
Explanation: The entire sequence is a wiggle sequence with differences (6, -3, 5, -7, 3).
Input: nums = [1,17,5,10,13,15,10,5,16,8]
Output: 7
Explanation: There are several subsequences that achieve this length. One is [1, 17, 10, 13, 10, 16, 8] with differences (16, -7, 3, -3, 6, -8).
Input: nums = [1,2,3,4,5,6,7,8,9]
Output: 2
Explanation: The sequence is strictly increasing, so the longest wiggle subsequence consists of only the first and last elements.
Constraints
- 1 <= nums.length <= 1000
- 0 <= nums[i] <= 1000
Figuring out "Wiggle Subsequence" can be solved using different approaches. We will first figure out the most intuitive approach and move to the optimal approach if exists. Let's sit with a pen and paper and figure out the algorithm !!
Optimal Approach
Intuition
Let's say we have an array of numbers, and we want to find the longest wiggle subsequence. How would you approach this problem?
A wiggle sequence? What does that mean?
Sure! A wiggle sequence is a sequence where the differences between consecutive numbers alternate in sign. In other words, an "up" wiggle means the current number is greater than the previous one, and a "down" wiggle means the current number is smaller than the previous one. For example, given an array [1, 7, 4, 9, 2, 5], one possible longest wiggle subsequence would be [1, 7, 4, 9, 2, 5] because it alternates between increasing and decreasing.
So we need to maximize the length of such a subsequence. The first thought that come to our mind is to generate all possible subsequences and filter out the longest valid one.
That’s a valid brute-force approach, but it would be highly inefficient. If the array has n elements, how many subsequences can we form?
The number of possible subsequences is 2^n, which is exponential in time complexity. That would be too slow for large inputs.
Exactly! Instead of checking all possibilities, let's break it down step by step. Suppose we take a simple example like [1, 2, 3, 4, 5]. What do we observe?
Well, it's strictly increasing, so there aren’t any "down" wiggles. The best we can do is pick the first and last elements: [1, 5].
Great! Now, what about [5, 4, 3, 2, 1]?
That’s strictly decreasing, so again, the best we can do is take [5, 1].
Exactly. Now, let’s take something like [1, 7, 4, 9, 2, 5]. How would we approach it?
We would track when the sequence goes up and when it goes down. If we go from 1 to 7, that’s an "up" move. Then from 7 to 4, that’s a "down" move. From 4 to 9, that’s an "up" move again. So, we see the pattern now!
Right! We are only interested in the points where the trend changes. Now, how do we efficiently track these changes?
Maybe we can keep two counters? One for when the sequence goes up and another for when it goes down?
Yes! Let's define:
- up – the length of the longest wiggle subsequence that ends with an "up" move.
- down – the length of the longest wiggle subsequence that ends with a "down" move.
Initially, both are 1 because any single element is trivially a valid wiggle subsequence.
That makes sense. So, as we iterate through the array, whenever we see an "up" move, we update up = down + 1, and whenever we see a "down" move, we update down = up + 1.
Why does an "up" move depend on the previous "down" move, and vice versa?
When we see an "up" move, it means we are extending a wiggle sequence that previously ended in a "down" move. So, we take the length of the longest "down" sequence and add 1 (up = down + 1).
Similarly, when we see a "down" move, we are extending a wiggle sequence that previously ended in an "up" move. So, we take the length of the longest "up" sequence and add 1 (down = up + 1).
Correct! Now, what if two consecutive elements are equal?
That wouldn't contribute to a wiggle because the sequence doesn't change direction. So, we just skip it!
Well summarized! Now, if you think about it, what kind of approach are we using here?
We are making the best possible choice at each step without looking ahead too much. This sounds like a greedy algorithm!
Exactly! The greedy approach works perfectly here because, at each step, we are ensuring that we capture every valid wiggle transition without needing to explore all subsequences.
Let's now see how our algorithm looks!
Wiggle Subsequence Algorithm
We implement a Wiggle Subsequence solution using a greedy approach.
- First, we define an array to store the sequence of numbers.
- In the wiggleMaxLength method, we iterate through the sequence while maintaining two values:
- up → Length of the longest wiggle sequence ending with an increasing wiggle.
- down → Length of the longest wiggle sequence ending with a decreasing wiggle.
- Update Conditions:
- If an increasing number follows a decrease, update up = down + 1.
- If a decreasing number follows an increase, update down = up + 1.
- Finally, return max(up, down) as the length of the longest possible wiggle subsequence.
Approach
- Initialize Two Counters:
- up = 1: Tracks the length of the longest wiggle sequence ending in an upward wiggle.
- down = 1: Tracks the length of the longest wiggle sequence ending in a downward wiggle.
- Iterate Through the Array:
- If nums[i] > nums[i - 1], update up = down + 1 (since we found an increase after a decrease).
- If nums[i] < nums[i - 1], update down = up + 1 (since we found a decrease after an increase).
- If nums[i] == nums[i - 1], ignore it (no wiggle).
- Return the Maximum of up and down, representing the longest wiggle subsequence.
Let us understand this with a video,
Dry-Run
Input: Sequence: {1, 5, 6, 8, 4, 3, 2, 9, 7}
Output: 5
Step-by-Step Dry Run:
Initialize:
up = 1 (Wiggle sequence ending with an increase)
down = 1 (Wiggle sequence ending with a decrease)
Process each element:
1 → 5 (Increase)
up = down + 1 → up = 2
5 → 6 (Increase)
No change
6 → 8 (Increase)
No change
8 → 4 (Decrease)
down = up + 1 → down = 3
4 → 3 (Decrease)
No change
3 → 2 (Decrease)
No change
2 → 9 (Increase)
up = down + 1 → up = 4
9 → 7 (Decrease)
down = up + 1 → down = 5
Final Output: Maximum wiggle subsequence length = max(up, down) = max(4, 5) = 5
Wiggle Subsequence Solution
Now let's checkout the "Wiggle Subsequence code" in C++, Java, Python and JavaScript.
"Wiggle Subsequence" Code in all Languages.
1. Wiggle Subsequence solution in C++ Try on Compiler
class Solution {
public:
int wiggleMaxLength(vector<int>& nums) {
// If the array is empty, return 0 as there's no wiggle sequence
if (nums.empty()) return 0;
int n = nums.size();
// If there's only one element, it's trivially a wiggle sequence of length 1
if (n < 2) return n;
// 'up' stores the longest wiggle subsequence ending with an increasing difference
// 'down' stores the longest wiggle subsequence ending with a decreasing difference
int up = 1, down = 1;
for (int i = 1; i < n; ++i) {
// If current element is greater than previous, increase 'up' count
if (nums[i] > nums[i - 1]) {
up = down + 1;
}
// If current element is smaller than previous, increase 'down' count
else if (nums[i] < nums[i - 1]) {
down = up + 1;
}
}
// Return the maximum of the two counts
return max(up, down);
}
};2. Wiggle Subsequence Solution in Java Try on Compiler
class Solution {
public int wiggleMaxLength(int[] nums) {
// If the array is empty, return 0 as there's no wiggle sequence
if (nums.length == 0) return 0;
int n = nums.length;
// If there's only one element, it's trivially a wiggle sequence of length 1
if (n < 2) return n;
// 'up' stores the longest wiggle subsequence ending with an increasing difference
// 'down' stores the longest wiggle subsequence ending with a decreasing difference
int up = 1, down = 1;
for (int i = 1; i < n; ++i) {
// If current element is greater than previous, increase 'up' count
if (nums[i] > nums[i - 1]) {
up = down + 1;
}
// If current element is smaller than previous, increase 'down' count
else if (nums[i] < nums[i - 1]) {
down = up + 1;
}
}
// Return the maximum of the two counts
return Math.max(up, down);
}
}3. Wiggle Subsequence Solution in Python Try on Compiler
class Solution:
def wiggleMaxLength(self, nums: List[int]) -> int:
# If the array is empty, return 0 as there's no wiggle sequence
if not nums:
return 0
n = len(nums)
# If there's only one element, it's trivially a wiggle sequence of length 1
if n < 2:
return n
# 'up' stores the longest wiggle subsequence ending with an increasing difference
# 'down' stores the longest wiggle subsequence ending with a decreasing difference
up = 1
down = 1
for i in range(1, n):
# If current element is greater than previous, increase 'up' count
if nums[i] > nums[i - 1]:
up = down + 1
# If current element is smaller than previous, increase 'down' count
elif nums[i] < nums[i - 1]:
down = up + 1
# Return the maximum of the two counts
return max(up, down)
4. Wiggle Subsequence solution in JavaScript Try on Compiler
/**
* @param {number[]} nums
* @return {number}
*/
var wiggleMaxLength = function(nums) {
// If the array is empty, return 0 as there's no wiggle sequence
if (nums.length === 0) return 0;
let n = nums.length;
// If there's only one element, it's trivially a wiggle sequence of length 1
if (n < 2) return n;
// 'up' stores the longest wiggle subsequence ending with an increasing difference
// 'down' stores the longest wiggle subsequence ending with a decreasing difference
let up = 1, down = 1;
for (let i = 1; i < n; ++i) {
// If current element is greater than previous, increase 'up' count
if (nums[i] > nums[i - 1]) {
up = down + 1;
}
// If current element is smaller than previous, increase 'down' count
else if (nums[i] < nums[i - 1]) {
down = up + 1;
}
}
// Return the maximum of the two counts
return Math.max(up, down);
};Wiggle Subsequence Complexity Analysis
Time Complexity: O(n)
The Wiggle Subsequence algorithm involves two key operations:
- Iterating through the sequence while maintaining up and down values:
- We traverse the array once, updating up and down based on increasing or decreasing trends.
- This operation takes O(n) time.
- Returning the maximum of up and down:
- A constant-time operation O(1).
Thus, the overall time complexity is: O(n) + O(1) = O(n), where n is the length of the sequence.
Space Complexity: O(1)
Auxiliary Space Complexity
- The algorithm only uses a few extra variables (up, down, n).
- No additional data structures are used.
- Thus, auxiliary space complexity is: O(1).
Total Space Complexity
- Input storage (array of size n): O(n)
- In-place iteration → No extra space
- Variables (constant space) → O(1)
Thus, the total space complexity is O(1).
Similar Problems
You are given a 0-indexed integer array nums of even length consisting of an equal number of positive and negative integers.
You should return the array of nums such that the the array follows the given conditions:
- Every consecutive pair of integers have opposite signs.
- For all integers with the same sign, the order in which they were present in nums is preserved.
- The rearranged array begins with a positive integer.
Return the modified array after rearranging the elements to satisfy the aforementioned conditions.
Given an integer array nums, return the length of the longest strictly increasing subsequence.