Top K Frequent Elements Solution In C++/Python/Java/JS
Problem Description
Given an integer array nums and an integer k, return the k most frequent elements. You may return the answer in any order.
Examples:
Input: nums = [1,1,1,2,2,3], k = 2
Output: [1,2]
Explanation: Frequency of 1 is 3 and frequency of 2 is 2, these two have the maximum frequency.
Input: nums = [11,11,2,4,4,5,4], k = 3
Output: [4,11]
Explanation: Frequency of 4 is 3 and frequency of 11 is 2, these two have the maximum frequency.
Constraints:
. 1 <= nums.length <= 10⁵
. -10⁴ <= nums[i] <= 10⁴
. k is in the range [1, the number of unique elements in the array].
. It is guaranteed that the answer is unique.
Brute Force Approach:
Okay, so here's the thought process:
What comes to mind after reading the problem statement?
We need to count the frequency of elements in nums array and then return the k elements with maximum frequency.
We can consider a brute force approach using two nested loops. In this approach, we first extract all unique elements and then count their frequencies manually.
After obtaining frequency counts, we can sort the elements based on their frequency and select the top K frequent ones. for each unique element, we count its frequency by iterating through the entire array again.
Once we have recorded the frequencies, we sort the elements based on their frequency in descending order. Finally, we select the top k elements from this sorted list.
How to Do It?
Extract Unique Elements:
Traverse the given array and store unique elements in a separate list or vector.
Count Frequency Using Nested Loops:
For each unique element, iterate over the original array to count its occurrences.
Store the frequency of each unique element in a separate array or vector.
Sort Elements Based on Frequency:
Use a simple sorting algorithm (like selection sort or bubble sort) to sort the unique elements based on their frequency in descending order.
Select the Top K Frequent Elements:
After sorting, pick the first K elements from the sorted list.
Return the Result:
Store and return the selected elements as the final answer.
Let's walk through an example:
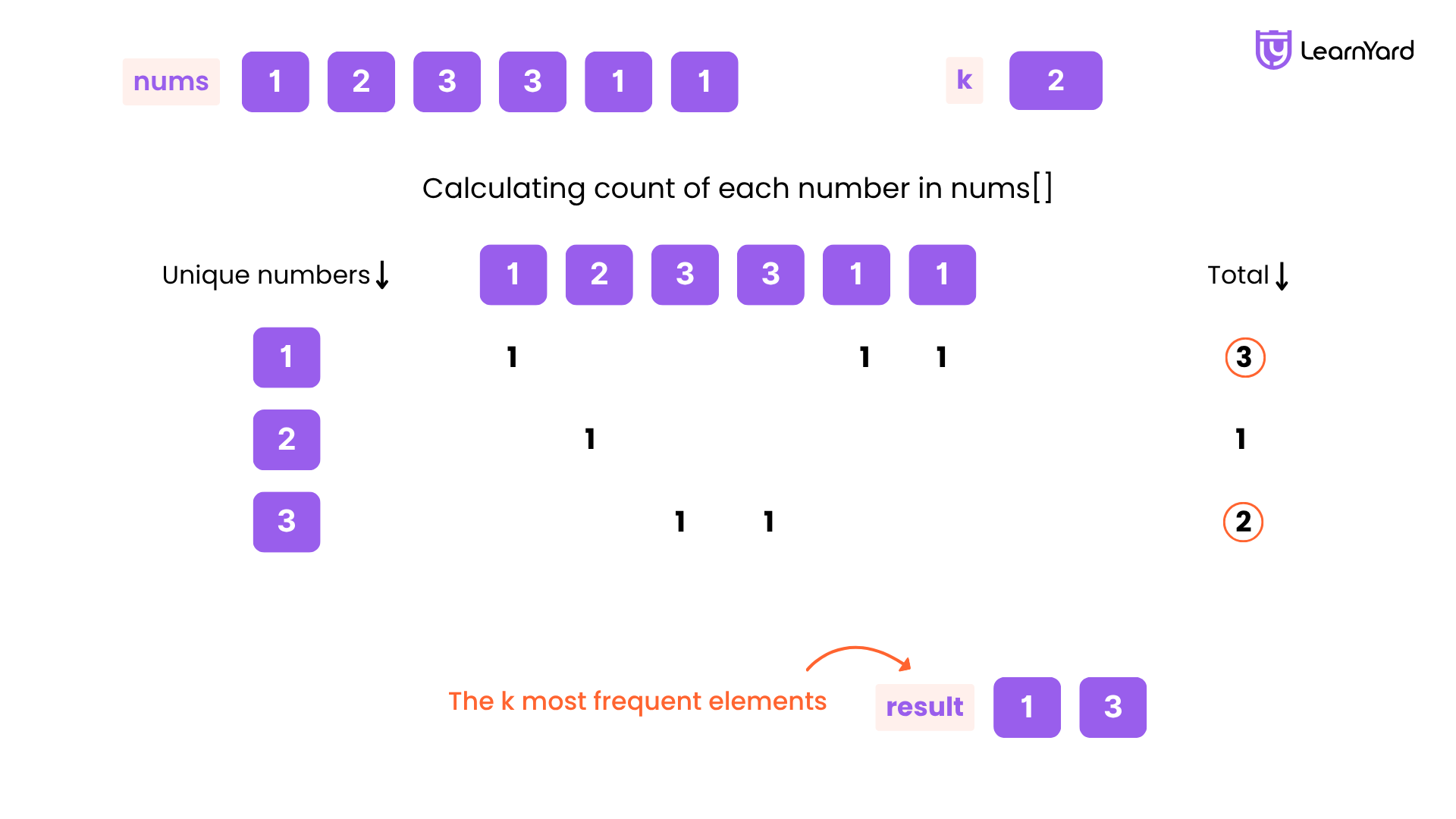
Let’s dry run the example: nums = [1, 1, 1, 2, 2, 3] and k = 2
1: Extract Unique Elements
We traverse nums and extract unique elements:
Unique Elements: {1, 2, 3}
2: Count Frequency Using Nested Loops
We iterate over nums for each unique element to count occurrences:
Unique Element Frequency Count
1 -> 3
2 ->2
3-> 1
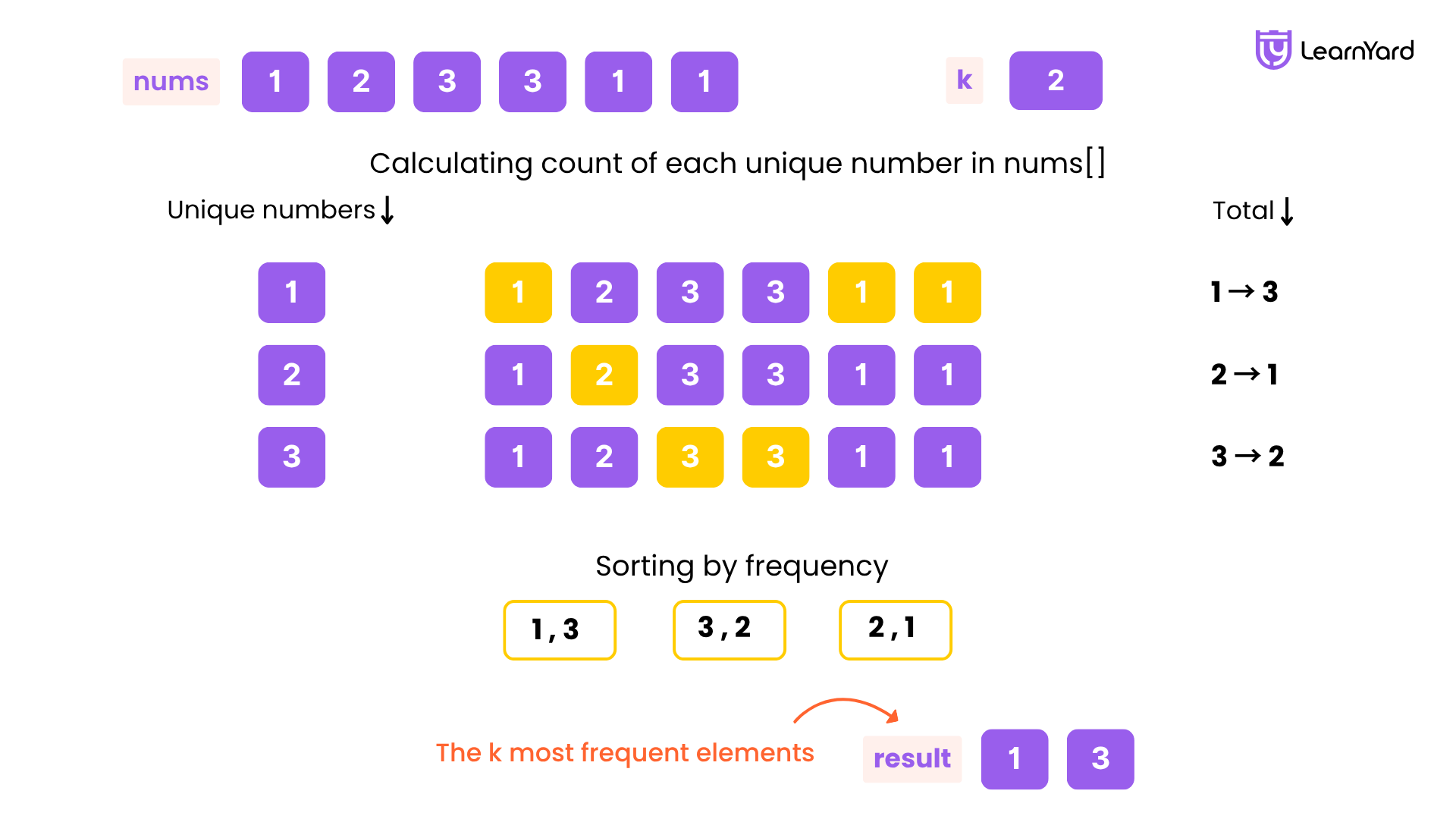
3: Sort by Frequency (Descending Order)
After sorting based on frequency, we get:
[{1, 3}, {2, 2}, {3, 1}]
4: Select the Top K Frequent Elements
Since k = 2, we take the first 2
result = {1, 2}
How to Code It Up
- Extract Unique Elements → Use a separate vector to store unique elements.
- Count Frequency → Use a nested loop to count occurrences of each unique element.
- Sort by Frequency → Sort the unique elements based on their frequency in descending order.
- Select Top K Elements → Pick the first K elements after sorting.
Code Implementation
1. C++ Try on Compiler
class Solution {
public:
vector<int> topKFrequent(vector<int>& nums, int k) {
vector<int> uniqueElements;
vector<int> frequency;
// Step 1: Extract unique elements
for (int i = 0; i < nums.size(); i++) {
bool found = false;
for (int j = 0; j < uniqueElements.size(); j++) {
if (nums[i] == uniqueElements[j]) {
found = true;
break;
}
}
if (!found) {
uniqueElements.push_back(nums[i]);
}
}
// Step 2: Count frequency using nested loops
for (int i = 0; i < uniqueElements.size(); i++) {
int count = 0;
for (int j = 0; j < nums.size(); j++) {
if (uniqueElements[i] == nums[j]) {
count++;
}
}
frequency.push_back(count);
}
// Step 3: Sort unique elements based on frequency
vector<pair<int, int>> freqPairs;
for (int i = 0; i < uniqueElements.size(); i++) {
freqPairs.push_back({frequency[i], uniqueElements[i]});
}
// Sort in descending order
sort(freqPairs.rbegin(), freqPairs.rend());
// Step 4: Select the top k elements
vector<int> result;
for (int i = 0; i < k; i++) {
result.push_back(freqPairs[i].second);
}
return result;
}
};2. Java Try on Compiler
class Solution {
public int[] topKFrequent(int[] nums, int k) {
List<Integer> uniqueElements = new ArrayList<>();
List<Integer> frequency = new ArrayList<>();
// Step 1: Extract unique elements
for (int num : nums) {
if (!uniqueElements.contains(num)) {
uniqueElements.add(num);
}
}
// Step 2: Count frequency using nested loops
for (int i = 0; i < uniqueElements.size(); i++) {
int count = 0;
for (int num : nums) {
if (uniqueElements.get(i) == num) {
count++;
}
}
frequency.add(count);
}
// Step 3: Sort unique elements based on frequency
List<Pair> freqPairs = new ArrayList<>();
for (int i = 0; i < uniqueElements.size(); i++) {
freqPairs.add(new Pair(frequency.get(i), uniqueElements.get(i)));
}
freqPairs.sort((a, b) -> Integer.compare(b.freq, a.freq)); // Sort in descending order
// Step 4: Select the top k elements
List<Integer> result = new ArrayList<>();
for (int i = 0; i < k; i++) {
result.add(freqPairs.get(i).element);
}
return result;
}3. Python Try on Compiler
def topKFrequent(nums, k):
unique_elements = []
frequency = []
# Step 1: Extract unique elements
for num in nums:
if num not in unique_elements:
unique_elements.append(num)
# Step 2: Count frequency using nested loops
for element in unique_elements:
count = 0
for num in nums:
if num == element:
count += 1
frequency.append(count)
# Step 3: Sort unique elements based on frequency
freq_pairs = list(zip(frequency, unique_elements))
freq_pairs.sort(reverse=True, key=lambda x: x[0])
# Step 4: Select the top k elements
result = [freq_pairs[i][1] for i in range(k)]
return result
4. Javascript Try on Compiler
/**
* @param {number[]} nums
* @param {number} k
* @return {number[]}
*/
function topKFrequent(nums, k) {
let uniqueElements = [];
let frequency = [];
// Step 1: Extract unique elements
for (let i = 0; i < nums.length; i++) {
if (!uniqueElements.includes(nums[i])) {
uniqueElements.push(nums[i]);
}
}
// Step 2: Count frequency using nested loops
for (let i = 0; i < uniqueElements.length; i++) {
let count = 0;
for (let j = 0; j < nums.length; j++) {
if (uniqueElements[i] === nums[j]) {
count++;
}
}
frequency.push(count);
}
// Step 3: Sort unique elements based on frequency
let freqPairs = [];
for (let i = 0; i < uniqueElements.length; i++) {
freqPairs.push([frequency[i], uniqueElements[i]]);
}
freqPairs.sort((a, b) => b[0] - a[0]); // Sort in descending order
// Step 4: Select the top k elements
let result = [];
for (let i = 0; i < k; i++) {
result.push(freqPairs[i][1]);
}
return result;
}
Complexity Analysis of Top K Frequent Element
Time complexity: O(n²)
Let's break down the time complexity of each step in the code:
Extract Unique Elements:
The loop iterates through the nums array, and for each element, it checks if it exists in uniqueElements using contains(), which takes O(n) in the worst case.
Since there are n elements in nums and each lookup in uniqueElements takes O(n) in the worst case, this results in O(n²) time complexity.
Count Frequency Using Nested Loops
We iterate over uniqueElements (at most n elements) and for each element, iterate through nums (size n) to count occurrences.
This results in O(n²) time complexity.
Sort Unique Elements Based on Frequency
Creating freqPairs takes O(n) since we iterate through uniqueElements. Sorting takes O(n log n).
Select the Top k Elements
Extracting k elements from the sorted list is O(k).
Overall Time Complexity: O(n²)
The dominant term in this approach is O(n²) from the nested loops used to count frequencies and extract unique elements. The sorting step is O(n log n), which is smaller than O(n²). Hence, the overall worst-case time complexity is: O(n²)
Space complexity: O(n)
Auxiliary Space Complexity: O(n)
Explanation: uniqueElements List
It Stores at most n unique elements → O(n) space.
frequency List
Stores frequency counts for each unique element → O(n) space.
freqPairs List
Stores pairs of (frequency, element) → O(n) space.
result List
Stores k elements → O(k) space.
Since we use multiple lists that store elements proportional to n, the overall space complexity is: O(n).
Total Space Complexity: O(n)
Explanation: The input array nums is given, which requires O(n) space.
Is the brute force approach efficient?
The current solution has a time complexity of O(n²) due to the use of nested loops for extracting unique elements and counting their frequencies. Given the constraint 1 ≤ nums.length ≤ 10⁵, this complexity is inefficient for large input sizes. In most competitive programming environments, problems can handle up to 10⁶ operations per test case, meaning that for n ≤ 10⁵, the solution with 10¹⁰ operations is not efficient enough.
When n approaches 10⁵, an O(n²) solution results in 10¹⁰ operations, When multiple test cases are involved, the total number of operations could easily exceed this limit and approach 10¹⁰ operations, especially when there are many test cases or the value of n increases.
Thus, while the solution meets the time limits for a single test case, the O(n²) time complexity poses a risk for Time Limit Exceeded (TLE) errors when handling larger input sizes or multiple test cases.
Optimization of Top K Frequent Element
In the brute force approach, determining the k most frequent elements requires scanning the array multiple times—once to count frequencies and again to sort the elements by their frequency. This results in an inefficient O(n²) time complexity due to repeated comparisons and nested iterations. As the input size grows the number of operations can reach 10¹⁰, making the approach impractical and leading to Time Limit Exceeded (TLE) errors.
A more efficient way to solve this problem is to store the frequency of elements in a data structure that allows constant-time lookups, such as a hashmap. Instead of iterating through the array multiple times, we can precompute the frequency of each element in O(n) time and store it in a hashmap.
What is a hash map?
A map (or hash map) is a data structure that stores data in pairs, where each pair consists of a {key, value}. You can think of it like a dictionary: for each unique key, there is an associated value. It helps us quickly look up, add, or update values based on keys.
We need to select the elements that have the highest frequency from the given nums array. To achieve this, we first need to count the frequency of each element. We can efficiently do this using a hashmap (unordered_map in C++), where the key is the element and the value is its frequency. Once we have the frequency count, we need to track top K elements.
Can you think of data structures where we can keep track of top K elements?
Yes, you’re right! We could use something like a Heap or priority queue to keep track of elements.
What is Heap?
A heap is a specialized tree-based data structure that allows for efficient retrieval of the smallest (min-heap) or largest (max-heap) element in O(1) time. However, insertion and deletion operations take O(log k) time. In our case, a max-heap ensures that the most frequent elements remain at the top, allowing us to efficiently extract the k most frequent elements.
The idea behind using a max-heap is that it allows us to efficiently maintain the k most frequent elements while discarding less frequent ones. We push elements into the heap based on their frequency, and if the heap size exceeds k, we remove the least frequent element. This ensures that at any point, the heap contains only the k most frequent elements. we can simply select the top k elements with the highest frequency.
How can we do that?
- Count Frequency:
Use a hashmap (unordered_map in C++) to store the frequency of each element in nums.
The key represents the element, and the value represents its frequency. - Use Max-Heap (Priority Queue) to Track the k Frequent Elements::
Convert the frequency map into a vector of pairs (element, frequency).
Sort this vector in descending order based on frequency. - Select Top k Elements:
After building the heap, we need to extract the top k elements with the highest frequency. - Return the Result:
Once we have the top k most frequent elements, return them as the final result.
Let's walk through an example:
Input: nums = [1,1,1,2,2,3], k = 2
So, we have 2 step's to perform in this problem:-
HashMap
Heap
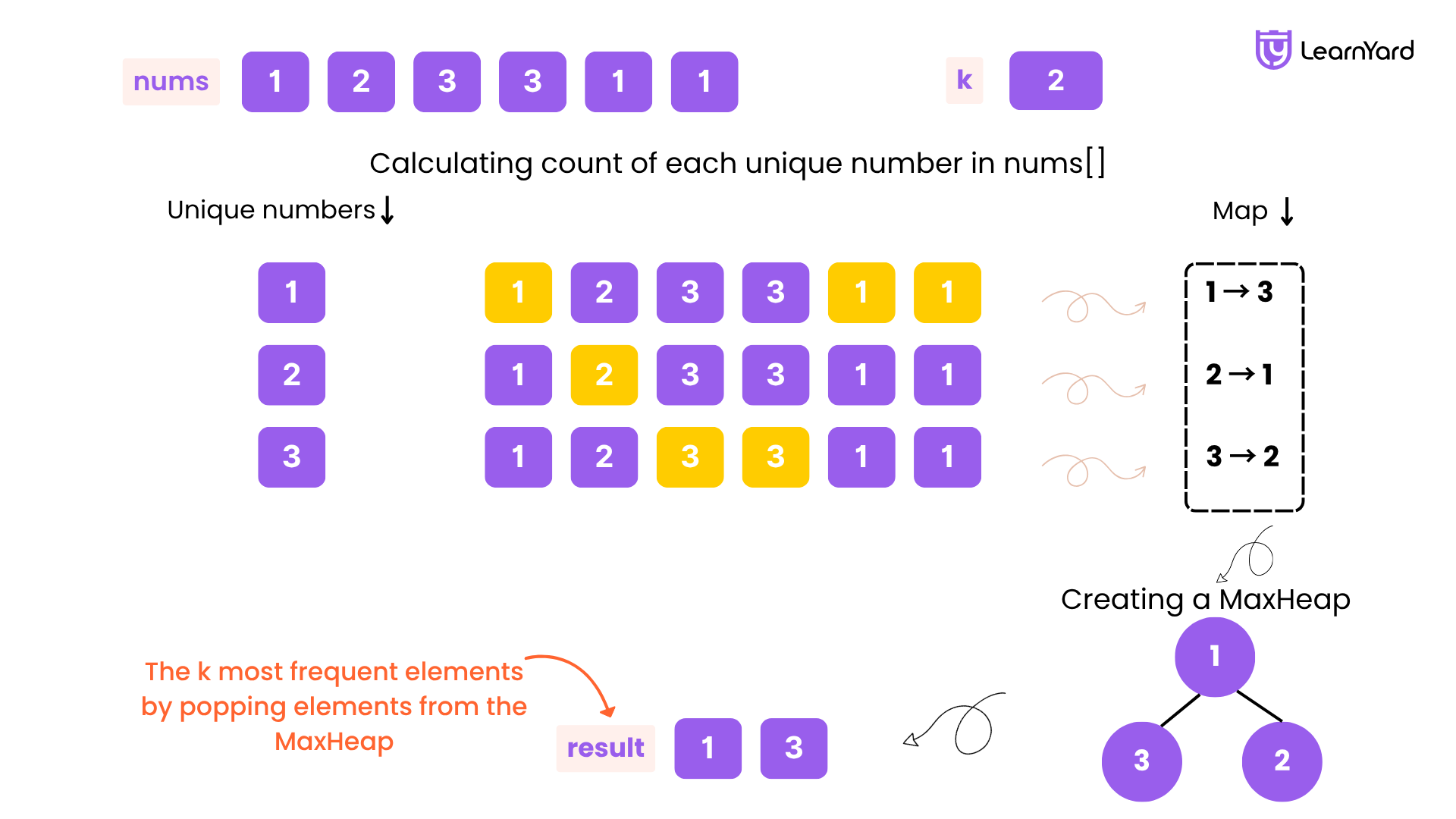
Step1: Make an Frequency map & fill it with the given elements.
[1,1,1,2,2,3]
------------------------------------------------
| 1 ---> 3 |
| 2 ---> 2 |
| 3 ---> 1 |
------------------------------------------------
Okay, so we just had completed our step no.1 now, it;s time to move to next step.
step2: Make an MaxHeap & fill it with keys & on the peek of our Heap we will be having most frequent elements.
HashMap :-
Key Value
1 ----> 3
2 ----> 2
3 ----> 1
Heap :-
| 1 |
| 2 |
| 3 |
------------
from the top of the heap we'll pop that no. of element requires in our array of k size.
Create result array res & store K frequent elements in it.
As, our K is 2 we gonna only store Most frequent K elements in our array, therefore in the result we get:- [1, 2]
How to convert it in code:
Count Frequency:
Use an unordered_map to store the frequency of each element.
The key represents the element, and the value represents its frequency.
Use a Max-Heap (Priority Queue):
use a max-heap (priority queue) Push elements into the heap in the form {frequency, element} so that the highest frequency stays at the top.
Extract the Top k Elements Efficiently:
Pop the top k elements from the heap and store them in the result.
Since a priority queue maintains the order dynamically, we avoid the need for sorting explicitly.
Code Implementation
1. C++ Try on Compiler
class Solution {
public:
vector<int> topKFrequent(vector<int>& nums, int k) {
unordered_map<int, int> freqMap;
// Step 1: Count frequencies
for (int num : nums) {
freqMap[num]++;
}
// Step 2: Max Heap using priority queue
priority_queue<pair<int, int>> maxHeap;
for (auto& pair : freqMap) {
maxHeap.push({pair.second, pair.first});
}
// Step 3: Extract k elements
vector<int> result;
for (int i = 0; i < k; i++) {
result.push_back(maxHeap.top().second);
maxHeap.pop();
}
return result;
}
};2. Java Try on Compiler
class Solution {
public int[] topKFrequent(int[] nums, int k) {
Map<Integer, Integer> freqMap = new HashMap<>();
// Step 1: Count frequencies
for (int num : nums) {
freqMap.put(num, freqMap.getOrDefault(num, 0) + 1);
}
// Step 2: Min Heap of size k
PriorityQueue<Integer> minHeap = new PriorityQueue<> (Comparator.comparingInt(freqMap::get));
for (int key : freqMap.keySet()) {
minHeap.add(key);
if (minHeap.size() > k) {
minHeap.poll();
}
}
// Step 3: Extract k elements from heap
int[] result = new int[k];
for (int i = k - 1; i >= 0; i--) {
result[i] = minHeap.poll();
}
return result;
}
}3. Python Try on Compiler
class Solution(object):
def topKFrequent(self, nums, k):
# Step 1: Count frequencies of numbers
freq_map = Counter(nums)
# Step 2: Use max heap to get top k elements
max_heap = [(-count, num) for num, count in freq_map.items()] # O(N)
heapq.heapify(max_heap)
# Step 3: Extract k elements from the heap
result = [heapq.heappop(max_heap)[1] for _ in range(k)]
return result
4. Javascript Try on Compiler
var topKFrequent = function(nums, k) {
let freqMap = new Map();
// Step 1: Count frequencies O(N)
for (let num of nums) {
freqMap.set(num, (freqMap.get(num) || 0) + 1);
}
// Step 2: Max Heap using a sorted array
let sortedNums = [...freqMap.keys()].sort((a, b) => freqMap.get(b) - freqMap.get(a)); // O(N log N)
// Step 3: Return first k elements
return sortedNums.slice(0, k);
};
// Example usage:
console.log(topKFrequent([1,1,1,2,2,3], 2)); // Output: [1, 2]
Top K Freq Elements Complexity Analysis
Time Complexity: O(nlogn)
Let's walk through the time complexity:
1.Counting Elements: We iterate through the nums array and store the frequency of each element in an unordered map.It takes O(n) time. where n is number of element in map.
2.Inserting Elements into a Max Heap
we insert each unique element (with its frequency) into the max heap.
Let U be the number of unique elements in nums.
It takes 𝑂(𝑈log𝑈) as Each insertion into the heap takes 𝑂(log𝑈) and we do this for U elements.
3: Extracting the Top K Elements
We extract the top k elements from the max heap. It takes 𝑂(𝐾log𝑈) as each extraction takes 𝑂(log𝑈) and we perform it K times.
Total time complexity: 𝑂(n) +𝑂(Ulog𝑈) +𝑂(𝐾log𝑈)
Worst case scenario:
If all elements in nums are unique, then U=n, and the complexity simplifies to:
O(n)+O(nlogn)+O(klogn) = O(nlogn).
Since K≤U, we can approximate 𝑂(𝐾log𝑈) ≤ 𝑂(nlogn)
meaning the overall complexity remains O(n log n).
Space Complexity:O(n)
Auxiliary Space Complexity: O(n)
Explanation:
1. HashMap
This stores the frequency of each unique element in nums.
In the worst case (when all elements in nums are unique), the map stores n key-value pairs. it requires O(n) space.
2. Max Heap
A priority queue (max-heap) is used to store the elements based on their frequency.
In the worst case, it stores n elements (one for each unique element).
The heap operations (push and pop) take O(log n) time but do not impact space usage. It takes O(n) space.
3. Result Vector
Stores the k most frequent elements.
Since k ≤ n, this takes O(k) space.
Since O(k) ≤ O(n) , the overall complexity simplifies to O(n).
Total Space Complexity: O(n)
Explanation: The input array nums is given, which requires O(n) space.
Can there be a better approach?
Yes, there’s definitely a smarter way to solve this problem.
The heap-based approach, while effective, has certain inefficiencies that can be improved. The primary bottleneck comes from the O(n log n) complexity due to heap insertions and deletions. Sorting elements using a heap is not always necessary, as we don’t need a fully sorted list—just the top k frequent elements. Additionally, heap operations introduce extra space overhead, making the approach less scalable for large inputs.
Instead of sorting elements explicitly, we can take advantage of the fact that the frequency of any element in nums is at most n. This means that instead of sorting based on frequency, we can group elements with the same frequency together. By storing elements in a structure where the index represents the frequency, we can efficiently retrieve the top k frequent elements without performing expensive heap operations.
This approach is known as bucket sort. We create an array of lists (buckets), where the index represents the frequency and each bucket stores elements with that frequency. By iterating from the highest frequency bucket downward, we can efficiently collect the k most frequent elements in O(n) time, making this an optimal alternative to the heap-based approach.
Why Bucket Sort?
- Avoid Explicit Sorting:
If we count the frequency of each number, we would typically sort the numbers by frequency, leading to O(n log n) complexity.
Instead, we can group elements by frequency in an array (bucket), reducing the time complexity to O(n). - Frequency Constraints:
The frequency of any element in nums is at most n , because there are n numbers in nums .
This means we can use an array of size n+1 (buckets) where the index represents frequency. - Efficiently Retrieve Top k Elements:
By iterating from the highest frequency bucket downward, we can efficiently collect the k most frequent elements without needing sorting or a heap.
// static image
Let's understand with an example:
Let's dry run on Input: nums = [1,1,1,2,2,3] and k = 2
Step 1: Count Frequency of Each Element
We use an unordered_map to count occurrences.
------------------------------------------------
| 1 ---> 3 |
| 2 ---> 2 |
| 3 ---> 1 |
------------------------------------------------
Step 2: Create Buckets
Since nums has n = 6 elements, we create buckets of size n + 1 = 7.
Each index i represents elements that appear exactly i times.
Initially: buckets = [[], [], [], [], [], [], []]
Step 3: Fill the Buckets
Now, we distribute elements into the respective frequency buckets.
1 appears 3 times → placed in buckets[3]
2 appears 2 times → placed in buckets[2]
3 appears 1 time → placed in buckets[1]
Buckets after inserting elements:
buckets = [[], [3], [2], [1], [], [], []]
Step 4: Collect the Top k Frequent Elements
Start from the highest frequency bucket (n down to 1).
Check buckets[6] → Empty
Check buckets[5] → Empty
Check buckets[4] → Empty
Check buckets[3] → Contains [1]
Pick 1 → result = [1]
k = 1 remaining
Check buckets[2] → Contains [2]
Pick 2 → result = [1, 2]
k = 0, so we stop.
Output: result = [1, 2]
How to code it up:
Build the Frequency Map:
Use an unordered_map<int, int> to store how many times each number appears in nums.
This helps in efficiently counting the frequency of each element.
Initialize Buckets:
Since the maximum frequency any element can have is n (where n is the size of nums), create a vector of vectors of size n + 1.
The index in this bucket represents the frequency, and each bucket stores elements that appear with that frequency.
Fill Buckets:
Iterate over the frequency map and place elements into their corresponding bucket based on their frequency.
Retrieve the Top k Elements Efficiently:
Traverse the buckets from the highest index (n) down to 1 to collect the most frequent elements.
Keep adding elements to the result until k elements are collected.
Return the Result:
Once we have collected k elements, return the final result array containing the k most frequent numbers.
Code Implementation
1. C++ Try on Compiler
class Solution {
public:
vector<int> topKFrequent(vector<int>& nums, int k) {
unordered_map<int, int> freqMap;
// Step 1: Count frequency of each element
for (int num : nums) {
freqMap[num]++;
}
int n = nums.size();
// Step 2: Create bucket array
vector<vector<int>> buckets(n + 1);
// Step 3: Fill the buckets based on frequency
for (auto& [num, freq] : freqMap) {
buckets[freq].push_back(num);
}
vector<int> result;
// Step 4: Iterate from highest frequency bucket to lowest
for (int i = n; i > 0 && k > 0; i--) {
for (int num : buckets[i]) {
result.push_back(num);
if (--k == 0)
break;
}
}
return result;
}
};2. Java Try on Compiler
class Solution {
public int[] topKFrequent(int[] nums, int k) {
Map<Integer, Integer> freqMap = new HashMap<>();
// Step 1: Count frequency of each element
for (int num : nums) {
freqMap.put(num, freqMap.getOrDefault(num, 0) + 1);
}
int n = nums.length;
// Step 2: Create bucket array
List<Integer>[] buckets = new ArrayList[n + 1];
// Step 3: Initialize each bucket as an empty list
for (int i = 0; i <= n; i++) {
buckets[i] = new ArrayList<>();
}
// Step 4: Fill the buckets based on frequency
for (Map.Entry<Integer, Integer> entry : freqMap.entrySet()) {
int freq = entry.getValue();
buckets[freq].add(entry.getKey());
}
List<Integer> result = new ArrayList<>();
// Step 5: Iterate from highest frequency bucket to lowest
for (int i = n; i > 0 && k > 0; i--) {
for (int num : buckets[i]) {
result.add(num);
if (--k == 0)
break;
}
}
return result;
}
}3. Python Try on Compiler
class Solution:
def topKFrequent(self, nums, k):
# Step 1: Count frequency of each element
freq_map = Counter(nums)
n = len(nums)
# Step 2: Create bucket array
buckets = [[] for _ in range(n + 1)]
# Step 3: Fill the buckets based on frequency
for num, freq in freq_map.items():
buckets[freq].append(num)
result = []
# Step 4: Iterate from highest frequency bucket to lowest
for i in range(n, 0, -1):
for num in buckets[i]:
result.append(num)
if len(result) == k:
return result4. Javascript Try on Compiler
/**
* @param {number[]} nums
* @param {number} k
* @return {number[]}
*/
var topKFrequent = function (nums, k) {
let freqMap = new Map();
// Step 1: Count frequency of each element
for (let num of nums) {
freqMap.set(num, (freqMap.get(num) || 0) + 1);
}
let n = nums.length;
// Step 2: Create bucket array
let buckets = Array.from({ length: n + 1 }, () => []);
// Step 3: Fill the buckets based on frequency
for (let [num, freq] of freqMap.entries()) {
buckets[freq].push(num);
}
let result = [];
// Step 4: Iterate from highest frequency bucket to lowest
for (let i = n; i > 0 && k > 0; i--) {
for (let num of buckets[i]) {
result.push(num);
if (--k === 0) break;
}
}
return result;
};Top K Freq Elements Complexity Analysis
Time Complexity: O(n)
Let's break down each step and analyze its complexity:
Counting the Frequency of Each Element (unordered_map)
We iterate through nums, and for each element, we update the frequency map. This takes O(n) time, where n is the number of elements in nums.
Filling the Buckets
We iterate over the elements in freqMap (which contains at most n unique elements in the worst case).Since each element is inserted into a bucket based on its frequency, this takes O(n) time.
Collecting the Top k Frequent Elements
We traverse the buckets array from the highest index downwards.
Each element is inserted into result at most once.
This also takes O(n) time in the worst case.
Overall Time Complexity: O(n)
Each step runs in O(n) time, so the total time complexity is O(n).
Space Complexity: O(n)
Auxiliary Space Complexity: O(n)
Explanation: Frequency Map
Stores the count of each unique number.
In the worst case (when all elements are unique), it takes O(n) space.
Buckets Array
We create a bucket array of size n + 1 with vectors.
The total number of elements stored across all buckets is n,
so this takes O(n) space.
Result Array
Stores the k most frequent elements.
This takes O(k) space.
Total Space Complexity: O(n)
Explanation: Consider nums has n elements it contribute O(n) to the total memory usage.
Similar Problems
Now we have successfully tackled this problem, let's try these similar problems.
Given an array of strings words and an integer k, return the k most frequent strings.
Return the answer sorted by the frequency from highest to lowest. Sort the words with the same frequency by their lexicographical order.
Given a string s, sort it in decreasing order based on the frequency of the characters. The frequency of a character is the number of times it appears in the string.
Return the sorted string. If there are multiple answers, return any of them.