Sum of Triplet Equal to Target in Array
To extend the approach we've used for finding two elements that sum up to a target value, we can apply the same logic to find three elements that sum up to a target value.
Given an array of integers, we need to check if there exist three distinct elements in the array such that their sum equals a given target value. If such a triplet exists, the function should print true; otherwise, it should print false.
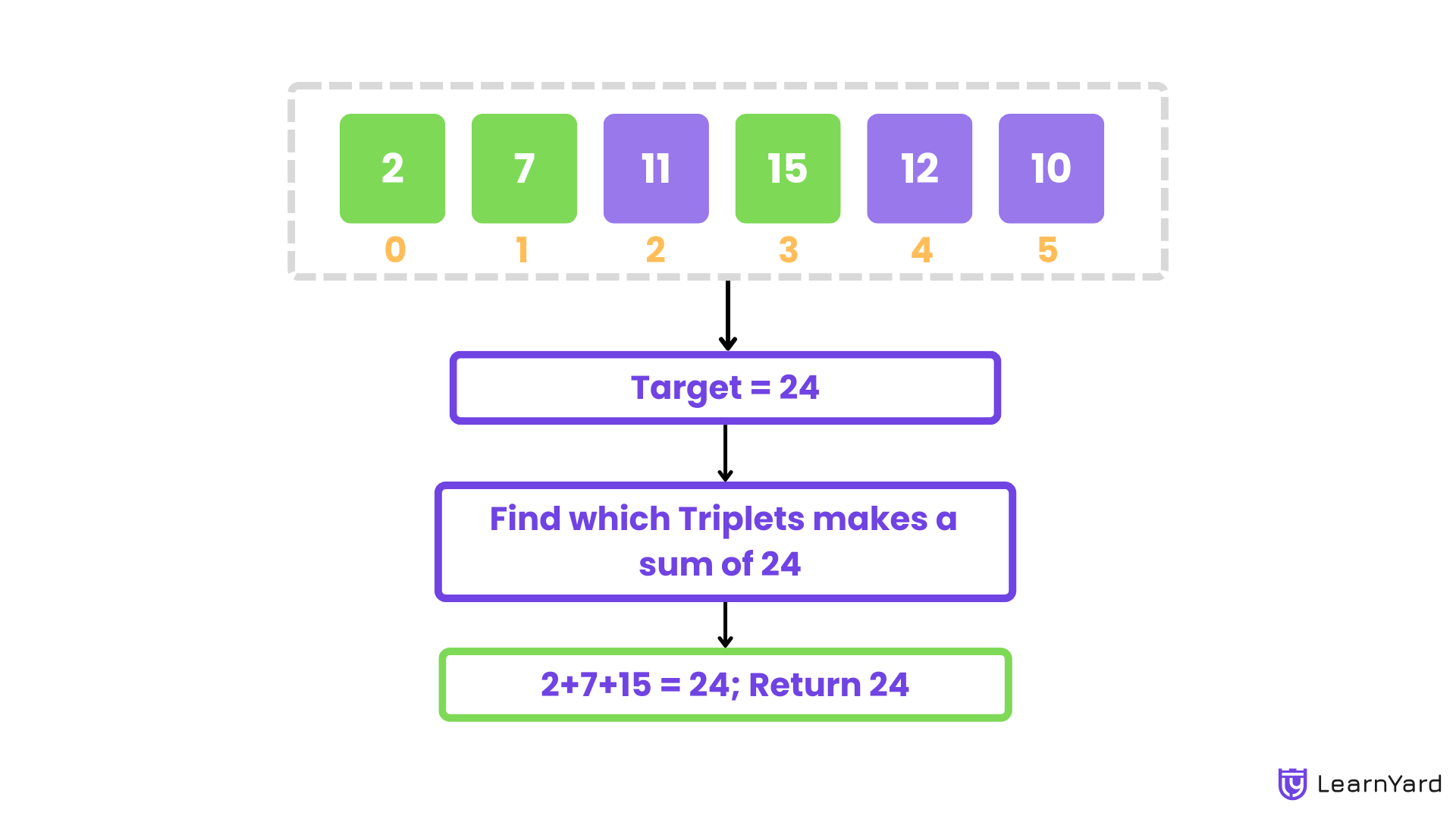
Example
Input: nums = [2, 7, 11, 15, 12, 10], target = 24
Output: true
Explanation: The elements 2, 7, and 15 sum up to 24.
Input: nums = [2, 7, 11, 15], target = 20
Output: false
Explanation: No three elements in the array sum up to 20.
Approach
To solve this problem, we want 3 numbers from the array to check whether their sum satisfies the target.
How can we get those three numbers?
To find the triplet of numbers that satisfies the target condition, we need to check all possible combinations of three different elements in the array. If we find any triplet that meets the condition, we can conclude that such a triplet exists and the answer will be true.
So, let's think about how we can systematically check each triplet of elements in the array. We can imagine iterating through each element in the array and checking it against every other 2 elements to see if their combined sum equals the target.
Detailed Explanation
We can say that we want a triplet that satisfies:
First Element + Second Element + Third Element = Target
Selecting the First Element:
We start by selecting the first element of the array. Let’s say our array is nums = [2, 7, 11, 15].
First Element = 2 (at index 0).
Selecting the Second Element:
Next, we look at each of the other elements in the array to find the second element. Since we need three distinct elements, we skip the index of the first element. Here, we skip index 0 where the value 2 is located.
- Skipping Index 0: The first element is at index 0, so we cannot select index 0 as the second element.
- Second Element Options: We can select any element from indices 1, 2, 3, 4, or 5 as the second element.
Selecting the Third Element:
Now, for every possible second element, we will select a third element from the remaining array. We have to consider different elements, so the index of the first element can't be the same as the second or third element, and the index of the second element can't be the same as the third element.
For example:
- At index 0 (first element 2), we skip considering index 0 for the second and third elements.
- At index 1, we select 7 as the second element, so the third element must be from the remaining indices.
We check:
- Add 2 + 7 + 11 → 2 + 7 + 11 = 20 (Not the target).
- Add 2 + 7 + 15 → 2 + 7 + 15 = 24 (This matches our target! We can immediately print true here and stop.)
Since we found a triplet that sums to the target value, we don't need to continue checking other combinations.
If we don’t find a matching triplet with 2 as the first element and 7 as the second element after considering all valid indices for the third element, we continue by changing the second element. Specifically, we move from 7 to the next element in the array and then check again for a valid triplet by considering all valid indices for the third element.
This process is repeated for every possible second element while keeping the first element fixed. Once we’ve exhausted all possibilities for the second element, we then change the first element from 2 to the value at the next index.
We repeat the same process: for each new first element, we iterate through all potential second elements, and for each pair of first and second elements, we consider all possible third elements.
By systematically changing the first and second elements and checking every combination of three elements, we ensure that we consider all possible triplets in the array. If no triplet is found that sums to the target value after all possibilities have been checked, we can confidently conclude that no such triplet exists.
How to considering All Triplets via Code?
The answer to this is by using a nested loop structure (a loop inside a loop inside another loop). The first loop is the outer loop, the second loop is the middle loop, and the third loop is the inner loop.
Outer Loop: This loop selects the first element of the triplet. For every position of this first element, we need to find the other two elements.
Middle Loop: This loop finds the second element to pair with the current first element. It skips that index which is the current index of the outer loop to avoid pairing an element with itself.
Inner Loop: This loop finds the third element to complete the triplet with the current first and second elements. It skips the indexes that are the same as the outer and middle loops to avoid using the same element twice.
Within the inner loop, we check if the sum of the elements selected by the outer, middle, and inner loops equals the target value.
Dry Run
Input Details
- Array: nums[] = {2, 7, 11, 15, 12, 10}
- Size of the array (n): 6
- Target sum: 24
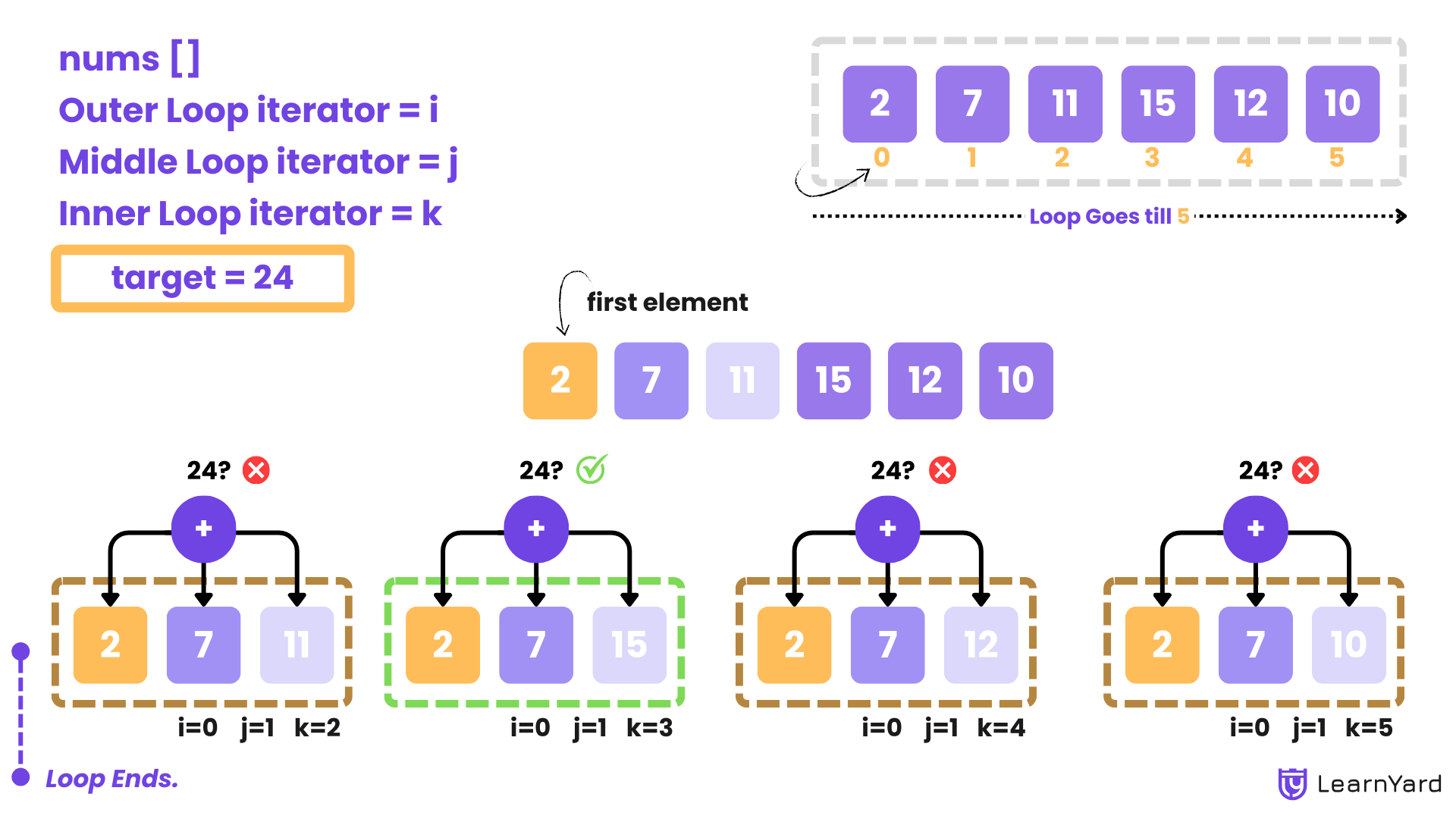
Outer Loop Iteration (Variable i)
The outer loop starts with i = 0. This loop selects the first number (nums[i]) for forming the triplet.
Outer Loop i = 0
- First number: nums[i] = nums[0] = 2
Middle Loop Iteration (Variable j)
The middle loop starts with j = 0. This loop selects the second number (nums[j]) for forming the triplet.
- Middle Loop j = 0
- nums[j] = nums[0] = 2
- Since i == j, this iteration is skipped.
- Middle Loop j = 1
- nums[j] = nums[1] = 7
Inner Loop Iteration (Variable k)
The inner loop starts with k = 0. This loop selects the third number (nums[k]) for forming the triplet.
- Inner Loop k = 0
- nums[k] = nums[0] = 2
- Since k == i or k == j, this iteration is skipped.
- Inner Loop k = 1
- nums[k] = nums[1] = 7
- Since k == i or k == j, this iteration is skipped.
- Inner Loop k = 2
- nums[k] = nums[2] = 11
- Check: nums[i] + nums[j] + nums[k] = 2 + 7 + 11 = 20
- The sum does not equal the target.
- Inner Loop k = 3
- nums[k] = nums[3] = 15
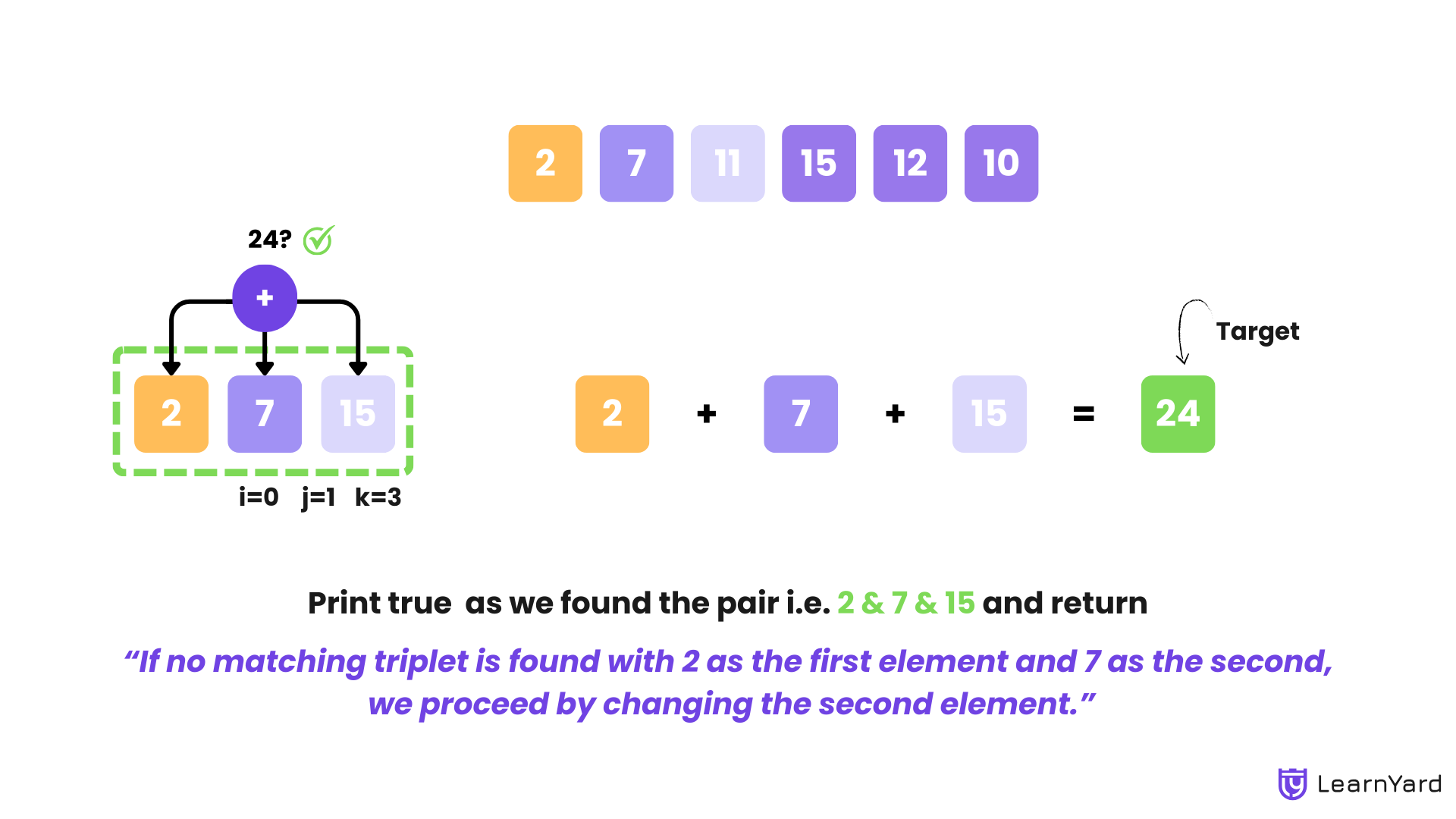
- Check: nums[i] + nums[j] + nums[k] = 2 + 7 + 15 = 24
- The sum equals the target.
- Output true and return from the function.
Function Ends
Since a triplet (2, 7, 15) that sums up to the target (24) is found, the program exits early without checking further combinations.
Output
The output is: true
Code for All Languages
C++
#include <iostream>
using namespace std;
// Function to check if any three numbers sum up to the target
void hasTripletWithSum(int nums[], int n, int target) {
// Outer loop: iterates through each element as the first element of the triplet
for (int i = 0; i < n; ++i) {
// Middle loop: iterates through each element as the second element of the triplet
for (int j = 0; j < n; ++j) {
// Skip if the indexes are the same as the first element
if (i == j) continue;
// Inner loop: iterates through each element as the third element of the triplet
for (int k = 0; k < n; ++k) {
// Skip if the indexes are the same as the first or second element
if (k == i || k == j) continue;
// Check if the sum of nums[i], nums[j], and nums[k] equals the target
if (nums[i] + nums[j] + nums[k] == target) {
// Print true if such a triplet is found and return
cout << "true";
return;
}
}
}
}
// Print false if no such triplet is found after checking all possibilities
cout << "false";
}
Java
import java.util.Scanner;
public class LearnYard {
// Function to check if any three numbers sum up to the target
public static void hasTripletWithSum(int[] nums, int n, int target) {
// Outer loop: iterates through each element as the first element of the triplet
for (int i = 0; i < n; i++) {
// Middle loop: iterates through each element as the second element of the triplet
for (int j = 0; j < n; j++) {
// Skip if the indexes are the same as the first element
if (i == j) continue;
// Inner loop: iterates through each element as the third element of the triplet
for (int k = 0; k < n; k++) {
// Skip if the indexes are the same as the first or second element
if (k == i || k == j) continue;
// Check if the sum of nums[i], nums[j], and nums[k] equals the target
if (nums[i] + nums[j] + nums[k] == target) {
// Print true if such a triplet is found and return
System.out.println("true");
return;
}
}
}
}
// Print false if no such triplet is found after checking all possibilities
System.out.println("false");
}
}
Python
# Function to check if any three numbers sum up to the target
def has_triplet_with_sum(nums, n, target):
# Outer loop: iterates through each element as the first element of the triplet
for i in range(n):
# Middle loop: iterates through each element as the second element of the triplet
for j in range(n):
# Skip if the indexes are the same as the first element
if i == j:
continue
# Inner loop: iterates through each element as the third element of the triplet
for k in range(n):
# Skip if the indexes are the same as the first or second element
if k == i or k == j:
continue
# Check if the sum of nums[i], nums[j], and nums[k] equals the target
if nums[i] + nums[j] + nums[k] == target:
# Print true if such a triplet is found and return
print("true")
return
# Print false if no such triplet is found after checking all possibilities
print("false")
Javascript
// Function to check if any three numbers sum up to the target
function hasTripletWithSum(nums, n, target) {
// Outer loop: iterates through each element as the first element of the triplet
for (let i = 0; i < n; i++) {
// Middle loop: iterates through each element as the second element of the triplet
for (let j = 0; j < n; j++) {
// Skip if the indexes are the same as the first element
if (i === j) continue;
// Inner loop: iterates through each element as the third element of the triplet
for (let k = 0; k < n; k++) {
// Skip if the indexes are the same as the first or second element
if (k === i || k === j) continue;
// Check if the sum of nums[i], nums[j], and nums[k] equals the target
if (nums[i] + nums[j] + nums[k] === target) {
// Print true if such a triplet is found and return
console.log("true");
return;
}
}
}
}
// Print false if no such triplet is found after checking all possibilities
console.log("false");
}
Time Complexity
The time complexity of this solution involves three nested loops.
Each loop runs n times, where n is the size of the input array. Therefore, the total number of iterations (or operations) performed by the three nested loops is n × n × n = n^3.
This leads to an overall time complexity of O(n³).
Space Complexity
Total Space Complexity: The total space complexity is O(n) because the input array takes O(n) space.
Auxiliary Space: The auxiliary space complexity is O(1) since only loop counters and comparison results are stored, which do not depend on the size of the input array.