Sum of Digit Differences of All Pairs Solution In C++/Java/Python/JS
Problem Description
Given an array nums consisting of positive integers where all integers have the same number of digits.
The digit difference between two integers is the count of different digits that are in the same position in the two integers.
Return the sum of the digit differences between all pairs of integers in nums.
Examples:
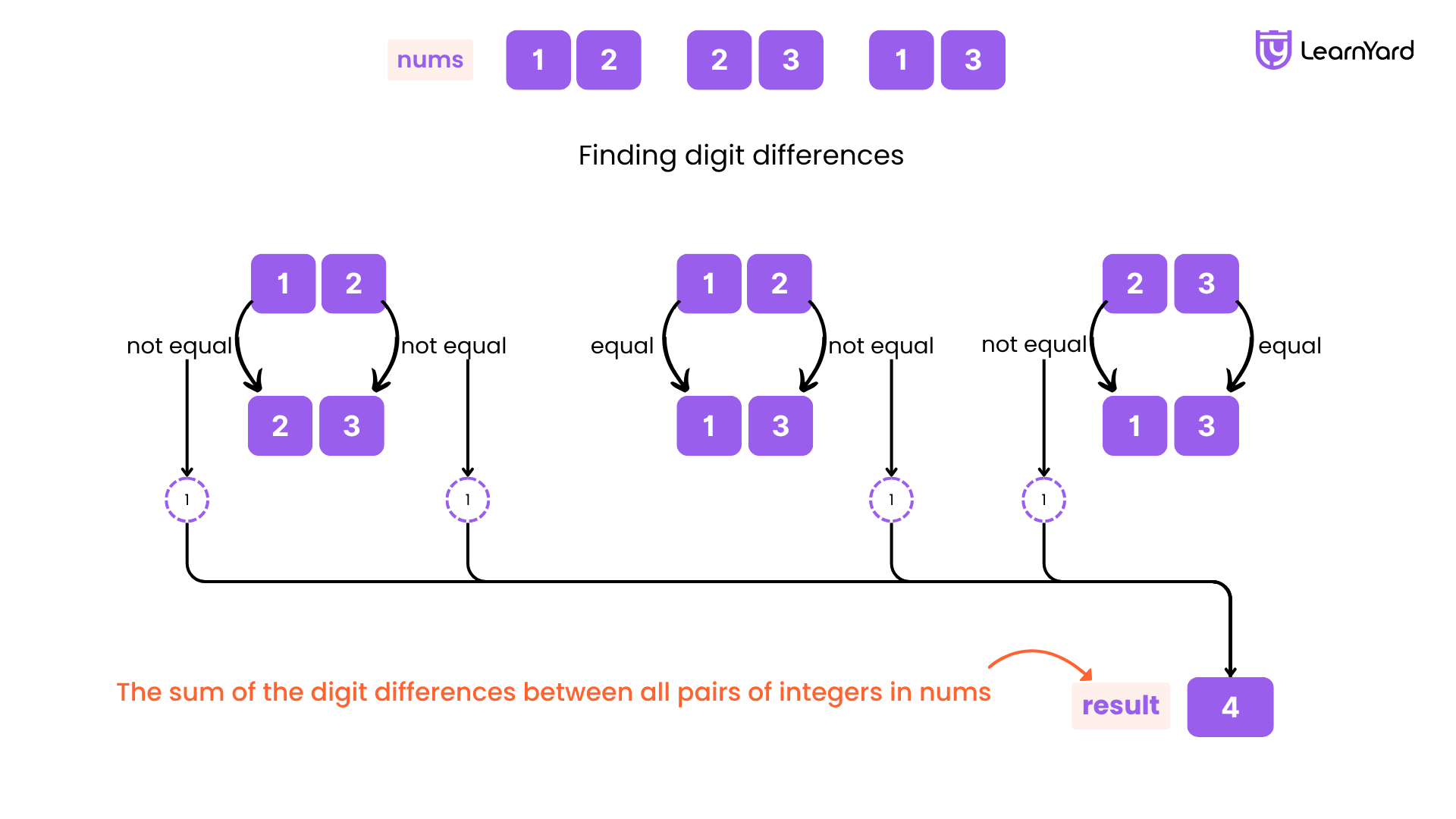
Input: nums = [13,23,12]
Output: 4
Explanation: We have the following:
- The digit difference between 13 and 23 is 1.
- The digit difference between 13 and 12 is 1.
- The digit difference between 23 and 12 is 2.
So the total sum of digit differences between all pairs of integers is 1+1+2 =4.
Input: nums = [10,10,10,10]
Output: 0
Explanation: All the integers in the array are the same. So the total sum of digit differences between all pairs of integers will be 0.
Constraints:
All integers in nums have the same number of digits.
1 <= nums[i] < 10^9
2 <= nums.length <= 10^5
The very first question that comes to our mind after reading the problem is: How can we calculate the digit differences between every pair of numbers in the array? Most of us already know that one straightforward way is to examine every possible pair in the array and compare their digits one by one. To build a solid understanding, let's start by exploring this brute-force approach in detail. This will help us grasp the core concept clearly before moving on to more optimized solutions.
Brute Force Approach
Intuition
Since we want to find the total digit differences between all pairs of numbers in the array, the first idea that comes to our mind is to compare every possible pair and count how many digits differ at the same positions. For example, if the array has numbers like 13 and 23, both having 2 digits, we can compare them digit by digit and count the mismatches.
Why Exactly Compare Digits at the Same Positions?
This is because the problem specifically asks us to count digit differences only at corresponding positions — that is, the first digit of one number with the first digit of the other, the second with the second, and so on.
Comparing Digits Using Nested Loops
To solve this problem using a brute-force approach, we need to compare every unique pair of numbers in the array. The most natural way to do this is by using nested loops.
- The outer loop will fix the first number in the pair.
- The inner loop will iterate over every number that comes after the first number in the array.
This ensures that we cover all possible pairs (i, j) where i < j, and that each pair is considered exactly once.
Once we have a valid pair of numbers, the next step is to compare their digits at each position. To do this efficiently, we convert both integers into strings. Since all numbers in the array have the same number of digits (as given in the problem), the string representations of these numbers will always be of equal length. This makes position-wise digit comparison straightforward.
Now that both numbers are in string form, we use a simple loop to traverse the digits from left to right, comparing them one by one:
- If the digits at the same position are equal, we move to the next position.
- If the digits differ, we increment a counter for this pair.
After processing all digit positions for a given pair, the count of digit differences is added to a running total that tracks the sum across all pairs in the array.
This method gives us a clear and direct way to simulate digit-wise comparison across pairs. It also lays the groundwork for understanding the nature of the problem deeply — especially how positional digit patterns can be exploited. Later, this foundational idea will help us reason about and implement optimized solutions using techniques like digit-position frequency counting.
Approach
Step 1: Initialize a Variable to Store the Result
Before starting any comparisons, we create a variable called totalDifference and initialize it to 0. This will be used to store the sum of digit differences between all pairs of numbers.
Since the array can be large and the answer may grow quickly, we use long long type to avoid overflow.
Step 2: Loop Through the Array to Fix the First Number in the Pair
We use an outer loop to fix the first number in the pair. This loop runs from the beginning of the array to the second-last element, since each element will be compared with every number that comes after it.
The loop runs from: i = 0 to i < nums.size()
This ensures that each number in the array gets a chance to act as the first number in the pair.
Step 3: Use an Inner Loop to Pick the Second Number in the Pair
Once we’ve fixed the first number using the outer loop, we use an inner loop to pick every number that comes after it in the array as the second number of the pair.
The inner loop runs from: j = i + 1 to j < nums.size()
This way, we generate all unique pairs (i, j) such that i < j.
Each pair will be compared only once, avoiding duplicate or reverse comparisons.
Step 4: Convert Both Numbers to Strings for Easy Digit Comparison
After selecting a pair of numbers, we convert both integers to their string representation.
This allows us to easily access and compare digits at the same position using character indexing, without having to extract digits mathematically.
Example:
If the pair is (13, 23), we convert them to strings "13" and "23"
Step 5: Compare the Digits at Each Position One by One
Now that both numbers are in string form, we go through each digit position (from left to right).
At every position, we check if the digits are different. If they are, we increment a local counter digitDiff which keeps track of how many digits are different for the current pair.
This loop runs from k = 0 to k < num1.length()
where num1 and num2 are the string versions of the two numbers.
Step 6: Add the Digit Difference of This Pair to the Total
After comparing all digits of the current pair, we add the value of digitDiff to our main variable totalDifference.
This captures how much this pair contributes to the overall answer.
Step 7: After All Loops, Return the Total Difference
Once all unique pairs have been processed and their digit differences have been added, we return the final value stored in totalDifference.
This value represents the total sum of digit differences between all unique pairs in the array.
Dry Run
Let’s do a detailed dry run of the brute-force approach using nested loops and digit-wise comparison for the input:
nums = [13, 23, 12]
We want to find the total sum of digit differences between all pairs of integers in the array. Two numbers are compared digit by digit in the same position, and we count how many of those digits are different.
Step 1: Initialize Variable for Storing the Result
We start by initializing a variable totalDifference = 0. This will hold the sum of digit differences across all valid pairs.
Step 2: Loop Through the Array to Fix the First Number
We begin our outer loop from index i = 0. This will fix the first number of the pair.
The outer loop will run until i = nums.length - 2.
Step 3: Use Inner Loop to Compare Each Pair (i, j)
For each fixed index i, we run an inner loop from j = i + 1 to the end of the array. This helps us form all unique pairs without repetition.
For every pair (i, j) , we convert both numbers into strings so we can access each digit easily by index.
Step 4: Compare Digits One by One
Now that we have both numbers in string format, we compare the digits at every index position.
If the digit at a particular position is different, we increase the digit difference count for that pair by 1.
After checking all digit positions, we add this count to our main result variable.
Iteration-wise Dry Run
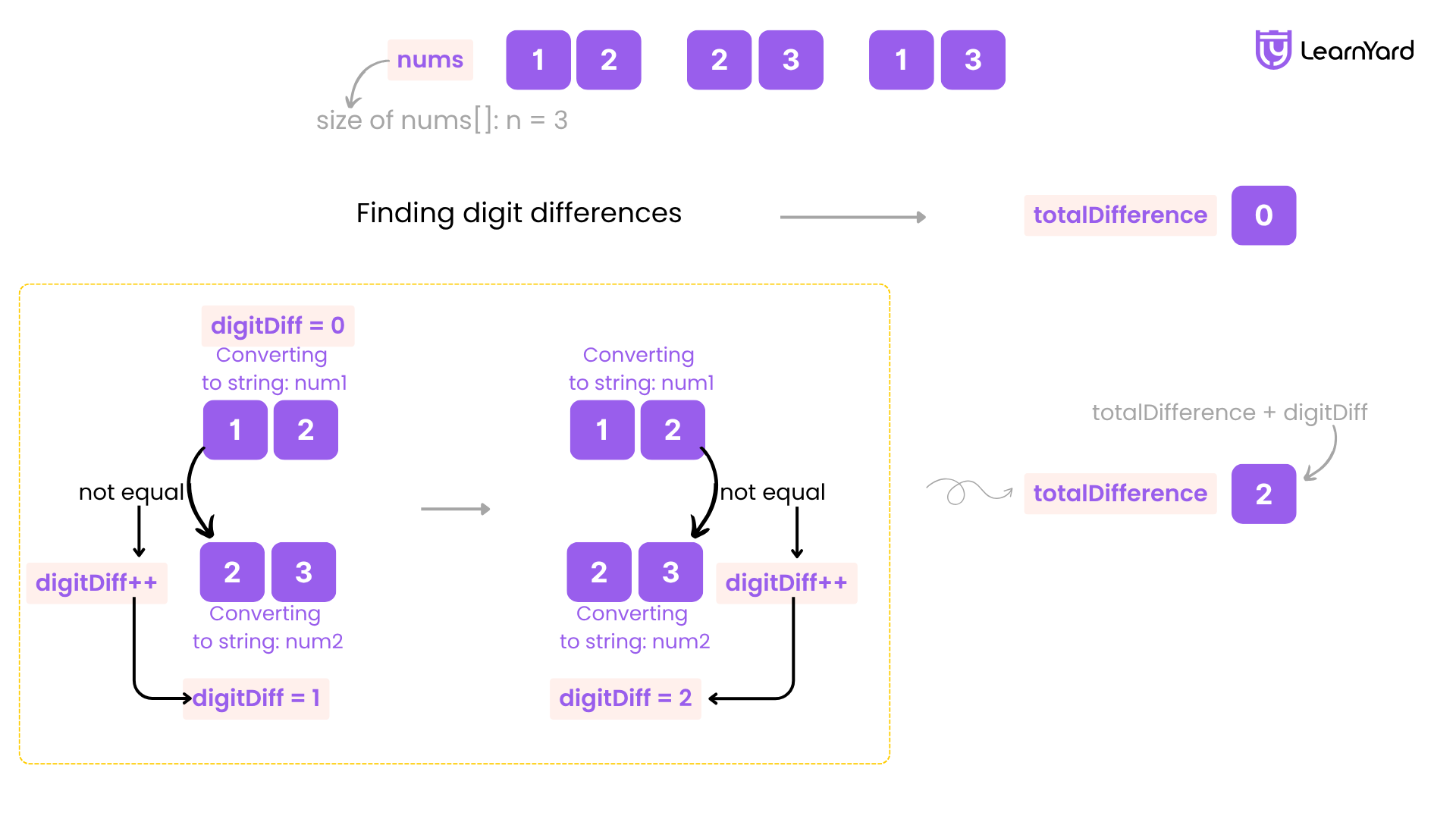
i = 0 → First number = 13
Start inner loop for all j > i
j = 1 → Second number = 23
Convert both to strings: "13" and "23"
Compare digits:
• Position 0: '1' vs '2' → different → count = 1
• Position 1: '3' vs '3' → same → count remains 1
Add to totalDifference → totalDifference = 1
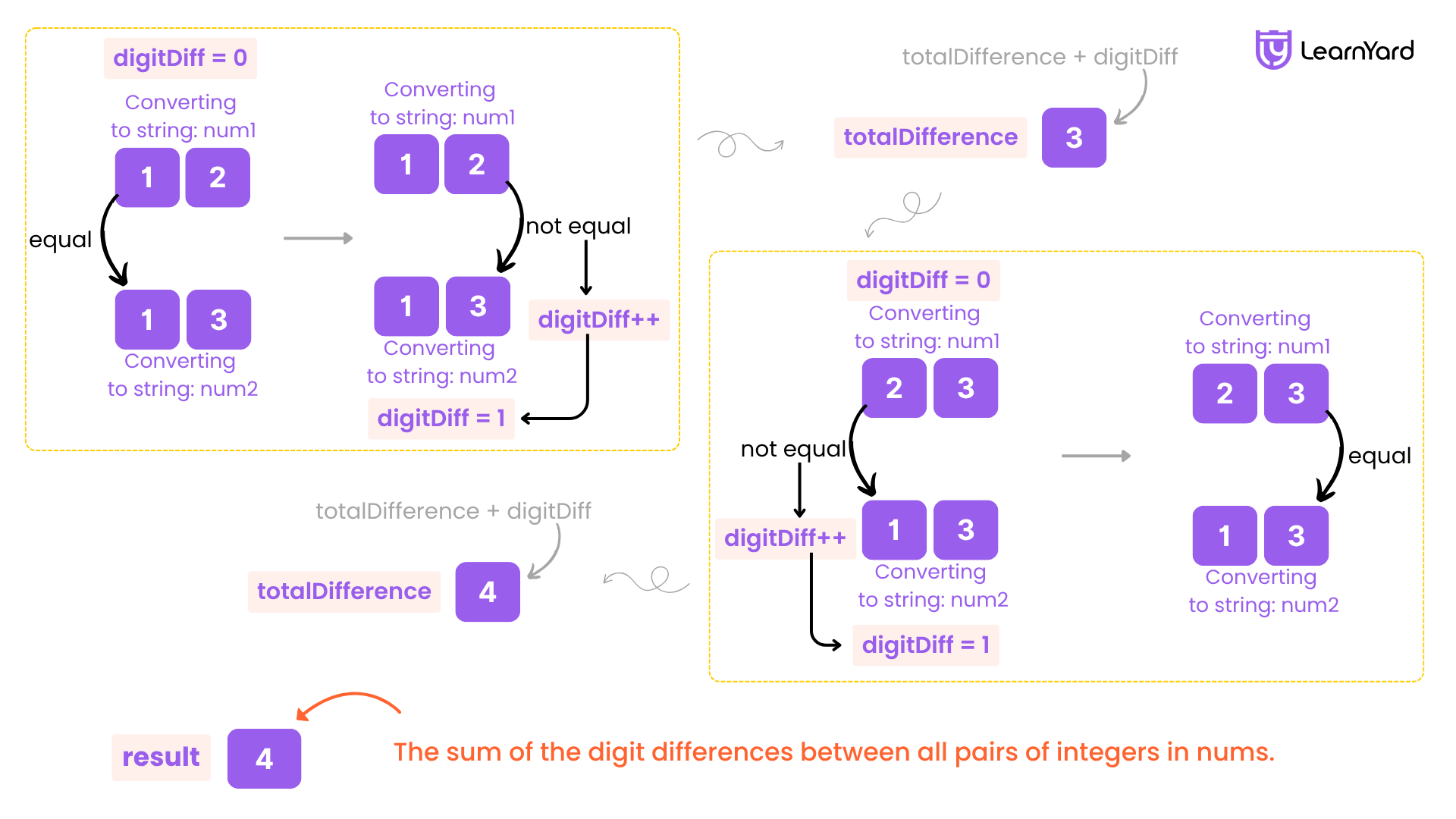
j = 2 → Second number = 12
Strings: "13" and "12"
Compare digits:
• Position 0: '1' vs '1' → same → count = 0
• Position 1: '3' vs '2' → different → count = 1
Add to totalDifference → totalDifference = 2
i = 1 → First number = 23
j = 2 → Second number = 12
Strings: "23" and "12"
Compare digits:
• Position 0: '2' vs '1' → different → count = 1
• Position 1: '3' vs '2' → different → count = 2
Add to totalDifference → totalDifference = 4
i = 2 → First number = 12
No further values of j → loop ends
Final Result
The total digit difference across all pairs is 4.
These come from the following comparisons:
• (13, 23) → 1 difference
• (13, 12) → 1 difference
• (23, 12) → 2 differences
Total = 1 + 1 + 2 = 4
Code for All Languages
C++
#include <iostream> // For input and output
#include <vector> // For using the vector data structure
#include <string> // For converting integers to strings
using namespace std;
class Solution {
public:
long long sumDigitDifferences(vector<int>& nums) {
// Step 1: Initialize a variable to store the result
long long totalDifference = 0;
int n = nums.size();
// Step 2: Loop through the array to fix the first number in the pair
for (int i = 0; i < n; i++) {
// Step 3: Use an inner loop to pick the second number in the pair
for (int j = i + 1; j < n; j++) {
// Step 4: Convert both numbers to strings for easy digit comparison
string num1 = to_string(nums[i]);
string num2 = to_string(nums[j]);
int digitDiff = 0;
// Step 5: Compare the digits at each position one by one
for (int k = 0; k < num1.length(); k++) {
if (num1[k] != num2[k]) {
digitDiff++;
}
}
// Step 6: Add the digit difference of this pair to the total
totalDifference += digitDiff;
}
}
// Step 7: After all loops, return the total difference
return totalDifference;
}
};
int main() {
int n;
cin >> n;
vector<int> nums(n);
//input the vector nums
for (int i = 0; i < n; i++) {
cin >> nums[i];
}
Solution sol;
long long result = sol.sumDigitDifferences(nums); //call the function
//Output the result
cout << result << endl;
return 0;
}
Java
import java.util.*; //for scanner and utility classes
class Solution {
public long sumDigitDifferences(int[] nums) {
// Step 1: Initialize variable for storing the result
long totalDifference = 0;
int n = nums.length;
// Step 2: Loop through the array to fix the first number
for (int i = 0; i < n - 1; i++) {
// Convert the fixed number to string
String num1 = String.valueOf(nums[i]);
// Step 3: Use inner loop to compare with all numbers after it
for (int j = i + 1; j < n; j++) {
// Convert the second number to string
String num2 = String.valueOf(nums[j]);
int digitDiff = 0;
// Step 4: Compare digits one by one
for (int k = 0; k < num1.length(); k++) {
if (num1.charAt(k) != num2.charAt(k)) {
digitDiff++; // Increase count if digits differ at this position
}
}
// Add this pair's digit difference to the total sum
totalDifference += digitDiff;
}
}
// Step 5: Return the final result after checking all pairs
return totalDifference;
}
}
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
// Input size of the array
int n = sc.nextInt();
int[] nums = new int[n];
// Input array elements
for (int i = 0; i < n; i++) {
nums[i] = sc.nextInt();
}
// Call the solution and print the result
Solution sol = new Solution();
long result = sol.sumDigitDifferences(nums);
System.out.println(result);
}
}
Python
from typing import List # For specifying the input and return types
class Solution:
def sumDigitDifferences(self, nums: List[int]) -> int:
total_difference = 0 # Step 1: Initialize variable for storing the result
n = len(nums)
# Step 2: Loop through the array to fix the first number
for i in range(n - 1):
num1 = str(nums[i]) # Convert the fixed number to string
# Step 3: Inner loop to compare with all numbers that come after it
for j in range(i + 1, n):
num2 = str(nums[j]) # Convert the second number to string
digit_diff = 0
# Step 4: Compare digits one by one
for k in range(len(num1)):
if num1[k] != num2[k]:
digit_diff += 1 # Increase count if digits differ at the same position
total_difference += digit_diff # Add this pair's difference to total
# Step 5: Return the final result after checking all pairs
return total_difference
# Driver Code
if __name__ == "__main__":
n = int(input()) # Input size of the array
nums = list(map(int, input().split())) # Input array elements
sol = Solution()
result = sol.sumDigitDifferences(nums)
print(result) # Output the final result
Javascript
/**
* @param {number[]} nums - Array of integers where all numbers have the same number of digits
* @return {number} - The total number of digit differences across all unique pairs
*/
var sumDigitDifferences = function(nums) {
let totalDifference = 0; // Step 1: Initialize variable for storing the result
let n = nums.length;
// Step 2: Outer loop to fix the first number
for (let i = 0; i < n - 1; i++) {
let num1 = nums[i].toString(); // Convert number to string to access individual digits
// Step 3: Inner loop to compare with every number after it
for (let j = i + 1; j < n; j++) {
let num2 = nums[j].toString(); // Convert second number to string
let digitDiff = 0;
// Step 4: Compare digits at each position
for (let k = 0; k < num1.length; k++) {
if (num1[k] !== num2[k]) {
digitDiff++; // Increase count if digits differ
}
}
totalDifference += digitDiff; // Add to the running total
}
}
// Step 5: Return the total digit differences
return totalDifference;
};
// Driver Code
const readline = require("readline");
const rl = readline.createInterface({
input: process.stdin,
output: process.stdout
});
let inputLines = [];
rl.on("line", function(line) {
inputLines.push(line.trim());
if (inputLines.length === 2) {
const n = parseInt(inputLines[0]);
const nums = inputLines[1].split(" ").map(Number);
const result = sumDigitDifferences(nums);
console.log(result);
rl.close();
}
});
Time Complexity : O(n²)
Outer Loop: O(n)
The outer loop runs from i = 0 to i = nums.length - 1.
Let’s denote:
- n= number of integers in the array
- d = number of digits in each number (since all numbers have the same number of digits)
So, the outer loop executes n times.
Inner Loop: O(n)
For each iteration of the outer loop, we run another loop from j = i + 1 to n - 1.
This gives approximately n iterations per outer loop pass in the worst case.
Therefore, the nested loop structure performs O(n²) pairwise comparisons in total.
Digit-by-Digit Comparison: O(1)
For every pair (i, j), we convert both numbers to strings and compare them digit by digit.
This takes O(d) time, since each number has d digits and we compare them one-by-one.
d can be maximum 9 , O(d) is just O(1)
Total Work per Pair: O(1)
For each of the O(n²) pairs, we do O(1) work to count digit differences.
Final Time Complexity: O(n² )
We perform O(1) operation for each of the O(n²) pairs of numbers.
So, the total time complexity is: O(n² )
Space Complexity: O(1)
Auxiliary Space Complexity: O(1)
This refers to any extra space used by the algorithm that is independent of the input and output space.
In our brute-force approach, we create:
- Temporary string versions of two numbers (converted from integers) for each pair.
- While comparing the digits of the two strings, we may use some space internally for string manipulation or indexing, which is proportional to d, the number of digits in each number.
Since this space is reused for every pair and does not grow with n, the auxiliary space used is O(1).
Hence, the auxiliary space complexity is O(1).
Total Space Complexity: O(n )
This includes the space required for:
- Input space: The input array nums contains n integers, so input space is O(n).
- Output space: We return a single number (the total sum of digit differences), which is O(1).
- Extra space used by the algorithm: As discussed above, O(1).
Combining all the space requirements:
Total Space Complexity = O(n) + O(1) = O(n)
Where:
- n is the number of elements in the array nums.
Will Brute-Force Work Against the Given Constraints?
For the current solution, the time complexity is O(n²), which is not suitable for n ≤ 10⁵. This means that for each test case, where the length of the array is at most 10⁵, the solution might not execute within the given time limits.
Since O(n²) results in a maximum of 10¹⁰ operations (for n = 10⁵), the solution is not expected to work well for larger test cases. In most competitive programming environments, problems can handle up to 10⁶ operations per test case, meaning that for n ≤ 10⁵, the solution with 10¹⁰ operations is not efficient enough.
When multiple test cases are involved, the total number of operations could easily exceed this limit and approach 10¹⁰ operations, especially when there are many test cases or the value of n increases.
Thus, while the solution meets the time limits for a single test case, the O(n²) time complexity poses a risk for Time Limit Exceeded (TLE) errors when handling larger input sizes or multiple test cases. This can be a challenge for competitive programming problems with larger inputs or numerous test cases.
We’ve seen the brute-force solution that compares every pair to count digit differences, but its nested loops make it too slow for large inputs. Instead of checking each pair directly, can we analyze digit frequencies at each position to avoid explicit comparisons? By leveraging these frequencies, we can speed up the process and eliminate the inefficiency. Let’s see how.
Optimal Approach
Intuition:
Let’s step back and think about what the digit difference between two numbers really means.
Suppose we are given two numbers with the same number of digits (for example: 123 and 143). We compare their digits position by position. At position 0 (units place), we have 3 vs 3 → same. At position 1, we have 2 vs 4 → different. At position 2, we have 1 vs 1 → same. So there is 1 digit difference between the two numbers.
Now, our goal is to find the total number of digit differences across all unique pairs in the array. If we try to do this by brute force, we would compare every pair and then every digit within the pair — that's expensive.
So instead of comparing all pairs directly, we flip our thinking:
Can we count how many different digits occur at each position across the array?
And then use that to figure out how many pairs have different digits at that position?
This gives birth to the idea of frequency counting by digit position using a frequency array.
What kind of Frequency array do we require?
Instead of comparing digits directly, we build a 2D frequency array freq[pos][digit] where:
- pos is the position of the digit (starting from 0 at units place),
- digit is the actual digit (from 0 to 9),
- freq[pos][digit] tells how many numbers have digit digit at position pos.
This allows us to group together all numbers that share the same digit at a particular position — without comparing each number with every other number.
So What’s the Plan?
- We first extract digits of each number one by one, and update our frequency table accordingly.
- Since every number has the same number of digits, we also keep track of how many positions are meaningful.
- Now for each position (say, position i), we do the following:
- For each digit d from 0 to 9, we know how many numbers have digit d at position i.
- Let’s call this count c.
- Then, there are n-c numbers that have a different digit at that position.
- So, digit d contributes c * (n - c) to the total digit differences (because there are c numbers with this digit and n - c without it).
- We do this for all digits at all positions.
- Since every pair gets counted twice (once as (a, b) and once as (b, a)), we divide the final result by 2.
Why is every pair counted twice?
When we compare digits using frequency, we're not directly forming number pairs — instead, we're counting how often digits differ at each position.
But for every pair of numbers like (A, B), the difference is also counted again when considering (B, A).
So each pair gets counted twice — once from A’s perspective and once from B’s.
That’s why we divide the final result by 2 — to make sure each pair is only counted once.
Why is This Efficient?
Instead of comparing every pair (which would be O(n²)), we just:
- Go through each number once to build the frequency table: O(n)
- Use a fixed number of digit positions (at most 9) and fixed digits (0–9), so contribution calculation is O(1) per position/digit.
That gives us an overall linear time solution, which is perfect for large inputs.
We turned a comparison problem into a counting problem, and that’s what makes this approach both elegant and optimal.
Approach
Step 1: Initialize Variables
We start by creating the variables that will help us in our computation:
n stores the size of the input array nums.
ans is initialized to 0 and will store the final result.
dig_cnt will eventually store how many digits are there in each number. All numbers are assumed to have equal digit length.
Step 2: Create the Frequency Table
Next, we prepare a 2D frequency array freq of size 9 x 10 initialized with zeros.
Here, freq[i][j] represents the number of times digit j appears at position i (from the right, 0-indexed) in all numbers.
Since nums[i] < 10⁹, the maximum number of digits a number can have is 9, and each digit can range from 0 to 9.
At this point, the table is ready but not filled.
Step 3: Iterate Through Each Number in the Array
We now process each number in the input array using a for loop.
For each number num, we copy it into a variable curr_no so that we can modify it.
We also initialize a variable curr_pos to track the current digit's position (starting from 0, which is the unit's place).
This step prepares for digit-by-digit extraction.
Step 4: Extract Each Digit of the Current Number and Update Frequency
We now enter a while loop that continues until curr_no becomes 0.
We extract the current digit using curr_no % 10.
We increment the frequency of that digit at the current position: freq[curr_pos][digit]++.
We then update curr_no using integer division by 10.
We also increment curr_pos to move to the next digit position (from right to left).
This fills the frequency table positionally for each number.
Step 5: Set dig_cnt to Total Number of Digits
After the while loop finishes for the current number, we set dig_cnt = curr_pos.
Since all numbers in the input are guaranteed to have the same number of digits, we only need to do this once.
This tells us how many meaningful positions we have to process later.
Step 6: Iterate Over Each Position from 0 to dig_cnt - 1
We now start analyzing the frequency data.
We loop through every digit position from 0 up to dig_cnt - 1.
These are the positions where actual digits appeared in the input numbers.
No need to go up to 8 if the numbers are shorter.
This step prepares us to process contribution from each position.
Step 7: For Each Position, Loop Over Digits 0 to 9
For each position, we now check all 10 possible digits (from 0 to 9).
We use another loop to go through digit j = 0 to 9.
If digit j occurred at this position in some numbers, then it can form pairs with all other numbers that do not have digit j at this position.
This step prepares the contribution calculation.
Step 8: Calculate Contribution of the Digit at the Current Position
We now calculate the contribution of digit j at position i to the overall digit difference.
If freq[i][j] numbers have digit j at position i, then:
There are n - freq[i][j] numbers that have a different digit at this position.
The number of differing pairs contributed by digit j at position i is:
freq[i][j] * (n - freq[i][j])
We add this to our ans.
This step is the core logic of the algorithm.
Step 9: Return Half of the Final Answer
Each pair is counted twice (once for (a, b) and once for (b, a)), so to get the correct answer:
We return ans / 2.
Let us understand this with a video,
Dry Run
Let’s do a step-by-step dry run of the optimized frequency-counting approach for the input:
nums = [13, 23, 12]
We aim to find the sum of digit differences across all pairs of numbers.
Step 1: Initialize all required variables
n = 3 (size of nums)
ans = 0 (final result to store the total sum of digit differences)
dig_cnt = 0 (to track number of digits, all numbers assumed to have equal length)
Step 2: Create the freq 2D vector
Create freq[9][10], initialized with zeros
Here, freq[pos][dig] stores how many times digit dig appears at position pos across all numbers
Step 3: Iterate through each number in nums
We process each number: 13, 23, and 12
Step 4: Extract each digit of the current number position-wise and update freq
Number = 13
→ Position 0 (units): digit = 3 → freq[0][3]++ → now 1
→ Position 1 (tens): digit = 1 → freq[1][1]++ → now 1
→ dig_cnt = 2 (this number has 2 digits)
Number = 23
→ Position 0: digit = 3 → freq[0][3]++ → now 2
→ Position 1: digit = 2 → freq[1][2]++ → now 1
→ dig_cnt = 2
Number = 12
→ Position 0: digit = 2 → freq[0][2]++ → now 1
→ Position 1: digit = 1 → freq[1][1]++ → now 2
→ dig_cnt = 2
Step 5: Iterate for each position pos where pos < dig_cnt
We loop over position pos = 0 and pos = 1
Step 6: Inner loop for each digit dig from 0 to 9
At each position, we calculate how many times each digit appeared, and how much it contributes to the total digit differences
Step 7: Calculate contribution of each digit and add to ans
Position 0 (units place):
freq[0][2] = 1 → contributes 1 × (3 - 1) = 2
freq[0][3] = 2 → contributes 2 × (3 - 2) = 2
→ Total from pos 0 = 4
Position 1 (tens place):
freq[1][1] = 2 → contributes 2 × (3 - 2) = 2
freq[1][2] = 1 → contributes 1 × (3 - 1) = 2
→ Total from pos 1 = 4
→ So, ans = 4 + 4 = 8
Step 8: Return ans / 2
Each pair has been counted twice (once for each direction), so we divide by 2
→ Final Answer = 8 / 2 = 4
Result:
The total sum of digit differences across all pairs of numbers is 4.
Code for All Languages
C++
#include <iostream> // For input and output functions like cin and cout
#include <vector> // For using the vector data structure
using namespace std;
class Solution {
public:
long long sumDigitDifferences(vector<int>& nums) {
// Step 1: Initialize all variables
int n = nums.size(); // Size of the input array
long long ans = 0; // Final result
int dig_cnt = 0; // Number of digits in each number (all numbers have same length)
// Step 2: Create a frequency array
// freq[pos][digit] stores how many times digit appears at position pos (0-based from unit place)
vector<vector<int>> freq(9, vector<int>(10, 0));
// Step 3: Iterate through each number in nums
for (int num : nums) {
int curr = num;
int pos = 0; // Start from unit digit
// Step 4: Extract each digit position-wise and update freq
while (curr > 0) {
int digit = curr % 10;
freq[pos][digit]++; // Increment frequency of this digit at this position
curr /= 10;
pos++;
}
// Step 5: Update dig_cnt to current digit count (same for all)
dig_cnt = pos;
}
// Step 6: Iterate for each digit position pos (from 0 to dig_cnt - 1)
for (int pos = 0; pos < dig_cnt; pos++) {
// Step 7: Iterate through each digit dig (0 to 9)
for (int dig = 0; dig < 10; dig++) {
// Step 8: Calculate contribution of this digit at this position
long long count = freq[pos][dig];
long long contribution = count * (n - count);
ans += contribution;
}
}
// Step 9: Return ans / 2 since each digit pair is counted twice
return ans / 2;
}
};
int main() {
int n;
cin >> n; // Input size of array
vector<int> nums(n);
for (int i = 0; i < n; i++) {
cin >> nums[i]; // Input each element
}
Solution sol;
cout << sol.sumDigitDifferences(nums) << endl; // Output the result
return 0;
}
Java
import java.util.*; //Scanner and utility classes
class Solution {
public long sumDigitDifferences(int[] nums) {
// Step 1: Initialize all variables
int n = nums.length; // Size of the input array
long ans = 0; // Final result
int dig_cnt = 0; // Number of digits in each number (all numbers have same length)
// Step 2: Create a frequency array
// freq[pos][digit] stores how many times digit appears at position pos (0-based from unit place)
int[][] freq = new int[9][10];
// Step 3: Iterate through each number in nums
for (int num : nums) {
int curr = num;
int pos = 0; // Start from unit digit
// Step 4: Extract each digit position-wise and update freq
while (curr > 0) {
int digit = curr % 10;
freq[pos][digit]++; // Increment frequency of this digit at this position
curr /= 10;
pos++;
}
// Step 5: Update dig_cnt to current digit count (same for all)
dig_cnt = pos;
}
// Step 6: Iterate for each digit position pos (from 0 to dig_cnt - 1)
for (int pos = 0; pos < dig_cnt; pos++) {
// Step 7: Iterate through each digit dig (0 to 9)
for (int dig = 0; dig < 10; dig++) {
// Step 8: Calculate contribution of this digit at this position
long count = freq[pos][dig];
long contribution = count * (n - count);
ans += contribution;
}
}
// Step 9: Return ans / 2 since each digit pair is counted twice
return ans / 2;
}
}
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt(); // Input size of array
int[] nums = new int[n];
for (int i = 0; i < n; i++) {
nums[i] = sc.nextInt(); // Input each element
}
Solution sol = new Solution();
System.out.println(sol.sumDigitDifferences(nums)); // Output the result
}
}
Python
from typing import List # For specifying the input and return types
class Solution:
def sumDigitDifferences(self, nums: List[int]) -> int:
# Step 1: Initialize all variables
n = len(nums) # Size of the input array
ans = 0 # Final result
dig_cnt = 0 # Number of digits in each number
# Step 2: Create a frequency array
# freq[pos][digit] stores how many times digit appears at position pos (0-based from unit place)
freq = [[0 for _ in range(10)] for _ in range(9)]
# Step 3: Iterate through each number in nums
for num in nums:
curr = num
pos = 0 # Start from unit digit
# Step 4: Extract each digit position-wise and update freq
while curr > 0:
digit = curr % 10
freq[pos][digit] += 1 # Increment frequency of this digit at this position
curr //= 10
pos += 1
# Step 5: Update dig_cnt to current digit count (same for all)
dig_cnt = pos
# Step 6: Iterate for each digit position pos (from 0 to dig_cnt - 1)
for pos in range(dig_cnt):
# Step 7: Iterate through each digit dig (0 to 9)
for dig in range(10):
# Step 8: Calculate contribution of this digit at this position
count = freq[pos][dig]
contribution = count * (n - count)
ans += contribution
# Step 9: Return ans // 2 since each digit pair is counted twice
return ans // 2
# Driver Code
if __name__ == "__main__":
n = int(input()) # Input size of the array
nums = list(map(int, input().split())) # Input array elements
sol = Solution()
result = sol.sumDigitDifferences(nums)
print(result) # Output the final result
Javascript
/**
* @param {number[]} nums - Array of integers where all numbers have the same number of digits
* @return {number} - The total number of digit differences across all unique pairs
*/
var sumDigitDifferences = function(nums) {
// Step 1: Initialize all variables
const n = nums.length; // Size of the array
let ans = 0; // Final result
let digCount = 0; // Number of digits in each number
// Step 2: Create a frequency array
// freq[pos][digit] stores how many times digit appears at position pos (0-based from unit place)
const freq = Array.from({ length: 9 }, () => Array(10).fill(0));
// Step 3: Iterate through each number in nums
for (let num of nums) {
let curr = num;
let pos = 0; // Start from unit digit
// Step 4: Extract each digit position-wise and update freq
while (curr > 0) {
const digit = curr % 10;
freq[pos][digit]++;
curr = Math.floor(curr / 10);
pos++;
}
// Step 5: Update digCount to current digit count (same for all)
digCount = pos;
}
// Step 6: Iterate for each digit position pos (from 0 to digCount - 1)
for (let pos = 0; pos < digCount; pos++) {
// Step 7: Iterate through each digit dig (0 to 9)
for (let dig = 0; dig < 10; dig++) {
// Step 8: Calculate contribution of this digit at this position
const count = freq[pos][dig];
const contribution = count * (n - count);
ans += contribution;
}
}
// Step 9: Return ans / 2 since each digit pair is counted twice
return Math.floor(ans / 2);
};
// Driver Code
const readline = require("readline");
const rl = readline.createInterface({
input: process.stdin,
output: process.stdout
});
let inputLines = [];
rl.on("line", function(line) {
inputLines.push(line.trim());
if (inputLines.length === 2) {
const n = parseInt(inputLines[0]);
const nums = inputLines[1].split(" ").map(Number);
const result = sumDigitDifferences(nums);
console.log(result);
rl.close();
}
});
Time Complexity: O(n)
Counting Digit Frequencies: O(n × D)
We iterate through each number in nums.
Let’s denote:
n = number of elements in nums
D = maximum number of digits in each number (bounded by 9)
For each number, we extract its digits one by one (at most D digits), which takes O(D) time.
Since we process n numbers, the total complexity becomes O(n × D).
Contribution Calculation per Digit Position: O(D × K) = O(1)
After collecting digit frequencies, we loop over each digit position (from 0 to dig_cnt - 1).
D is the number of digit positions (≤ 9).
For each position, we loop through each digit from 0 to 9 (total K = 10 digits).
Since both D and K are small fixed constants, this part takes constant time overall, i.e., O(1).
Final Arithmetic: O(1)
We perform a single division by 2 to adjust for double counting.
This is a constant time operation.
Total Time per Number: O(D)
Each number is processed by extracting its digits, which takes O(D) time.
Final Time Complexity: O(n)
Since we process n numbers, each taking O(D) time, and D is bounded (≤ 9), the overall time complexity simplifies to O(n).
Space Complexity: O(1)
Auxiliary Space Complexity: O(1)
This refers to any extra space used by the algorithm that is independent of the input and output sizes.
In this optimized approach, we create:
- A 2D frequency matrix freq of size 9 × 10, which keeps track of the count of each digit (0–9) at every possible digit position (up to 9 positions, since numbers are < 10⁹).
- A few variables: n, ans, dig_cnt, and loop variables.
All of these are fixed-size allocations and do not grow with the size of the input list.
Hence, the auxiliary space used is constant.
Thus, the auxiliary space complexity is O(1).
Total Space Complexity: O(n)
This includes space for:
1. Input Space:
- The input array nums of length n.
→ Space = O(n)
2. Output Space:
- We only return a single integer ans representing the total digit differences, which takes O(1) space.
→ Space = O(1)
3. Auxiliary Space:
- As analyzed above, this is O(1).
Final Total Space Complexity = O(n) + O(1) + O(1) = O(n)
Learning Tip
Now we have successfully tackled this problem, let's try this similar problem.
You are given an array nums consisting of positive integers where all integers have the same number of digits. The digit difference between two integers is the count of different digits that are in the same position in the two integers.
Return the sum of the digit differences between all pairs of integers in nums.