Subarrays with K Different Integers Solution In C++/Java/Python/JS
Problem Description
Given an integer array nums and an integer k, return the number of good subarrays of nums.
A good array is an array where the number of different integers in that array is exactly k.
For example, [1,2,3,1,2] has 3 different integers: 1, 2, and 3.
A subarray is a contiguous part of an array.
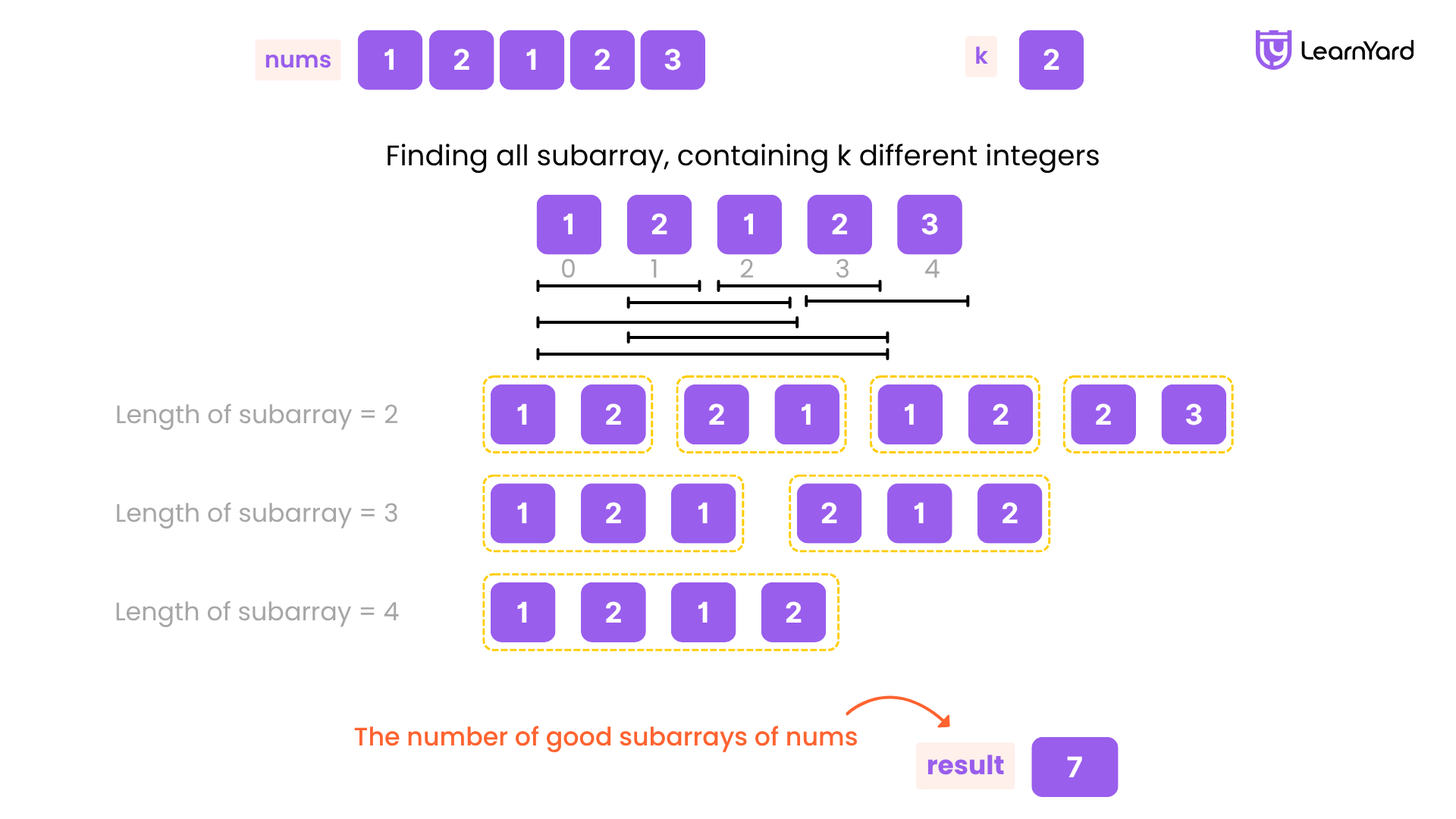
Examples:
Input: nums = [1,2,1,2,3], k = 2
Output: 7
Explanation: Subarrays formed with exactly 2 different integers: [1,2], [2,1], [1,2], [2,3], [1,2,1], [2,1,2], [1,2,1,2]
Input: nums = [1,2,1,3,4], k = 3
Output: 3
Explanation: Subarrays formed with exactly 3 different integers: [1,2,1,3], [2,1,3], [1,3,4].
Constraints:
- 1 <= nums.length <= 2 * 104
- 1 <= nums[i], k <= nums.length
In this problem, we need to count all the subarrays that contain exactly `k distinct elements.
The first idea that naturally comes to mind is that we could go through every possible subarray of the given array and, for each one, check how many unique elements it has.
This is what we will explore in the brute force approach let's check it out...
Brute Force Approach
Intuition
The most straightforward approach we can think of is to go through every possible subarray of the given array.
How to Visit Every Subarray of an Array Using Nested Loops?
To implement this, we first fix the starting index i of the subarray in the array using an outer loop. This loop runs from i = 0 up to i = array.size - 1, ensuring that all possible starting points are covered.
For each fixed starting index i, we use an inner loop with index j to define the ending index of the subarray. This inner loop runs from j = i to j < array.size. We start with an empty subarray and append elements from array[j] one by one. This manual construction of subarrays helps beginners understand how subarrays can be formed using indices, without relying on built-in slice or subarray functions.
Note: We can also replace the inner loop and use built-in slicing methods instead, depending on the language and level of abstraction preferred.
Let’s consider an example to clarify this process. Suppose the array is: [1, 2, 3]. Using the nested loops:
- At i = 0, we generate:
- j = 0 → subarray: [1]
- j = 1 → subarray: [1, 2]
- j = 2 → subarray: [1, 2, 3]
- At i = 1, we generate:
- j = 1 → subarray: [2]
- j = 2 → subarray: [2, 3]
- At i = 2, we generate:
- j = 2 → subarray: [3]
Each subarray starts at index i and ends at index j. After generating these subarrays, we can proceed to apply any additional logic needed, such as checking for a particular sum, length, or pattern.
For each subarray, we simply count the number of unique elements it contains.
If the number of unique elements is exactly k, we increase our count.
Once we’ve checked all the subarrays, we just return the total count of those that had exactly k distinct elements.
It’s a basic and easy-to-understand method, though not the most efficient for large arrays.
How to Find Unique Elements in the Subarray?
To determine the number of unique elements in a subarray, we can use a key-value data structure that allows storing elements along with how many times they occur. This structure lets us efficiently keep track of which elements have appeared and how often.
Here’s how it works:
- As we go through the subarray, we insert each element into the data structure.
- The element itself serves as the key, and the value represents the count of how many times that element has appeared so far.
- If the element has already been added before, we simply update its count.
- Once we've finished processing the subarray, the number of unique elements is equal to the number of keys in the data structure.
This method is a clear and effective way to count distinct elements in a subarray by keeping track of their frequencies. It doesn’t rely on any specific programming language and can be implemented using any environment that supports basic key-value storage.
Subarrays with K Different Integers Algorithm
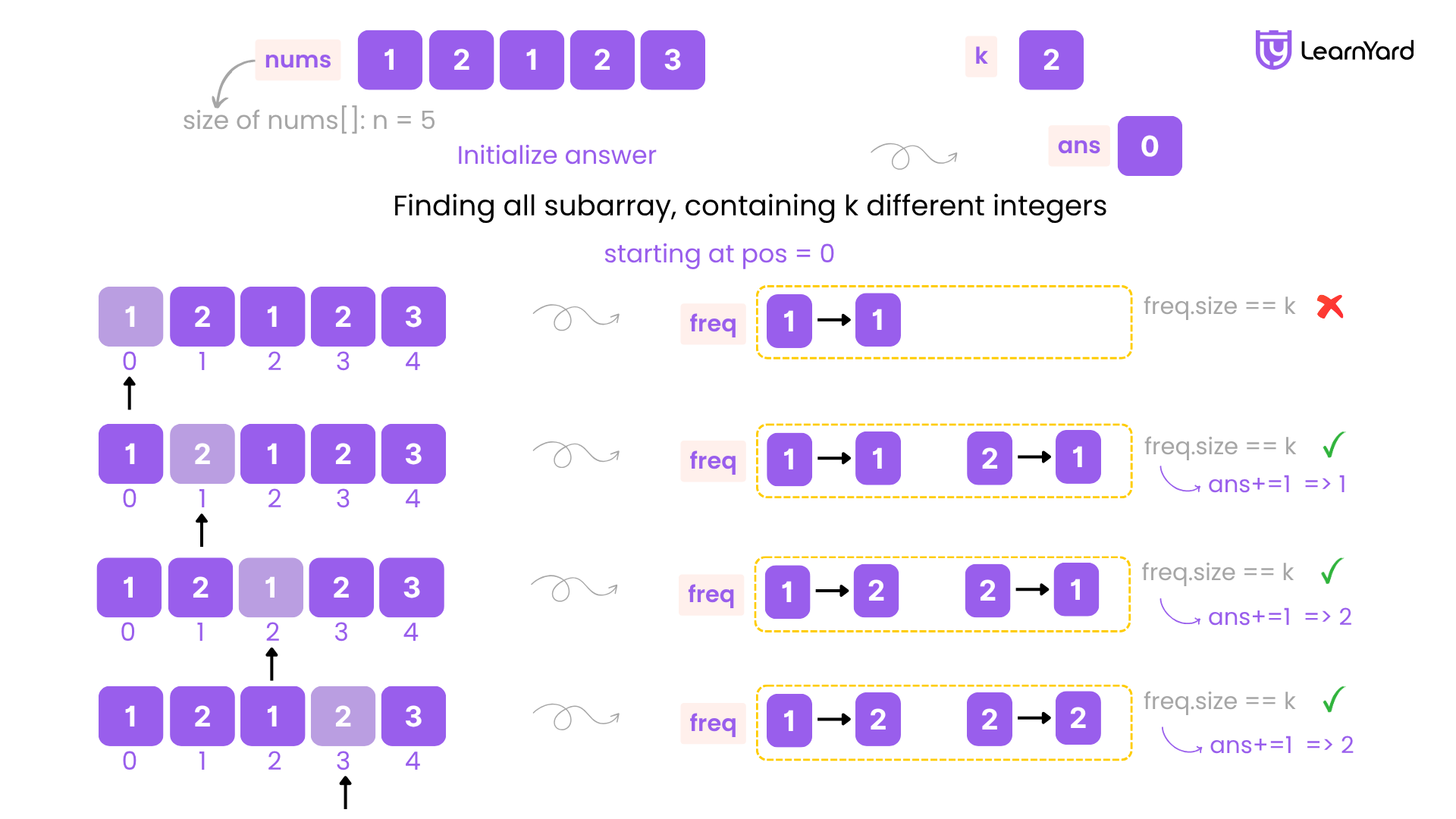
Step 1. Initialize basic variables
First, determine the size of the input array. Then, initialize a variable to store the final count of valid subarrays. You’ll also need a data structure (like a map or dictionary) to keep track of how many times each element appears in the current window or subarray. This will help in managing the count of distinct elements efficiently.
Step 2. Start the outer loop to pick the index of the subarray
Use a loop variable i that runs from 0 to n-1. For each new starting index, clear the freq map since we are checking a new subarray.
Step 3. Start the inner loop to pick the ending index of the subarray
Use another loop variable, j, that runs from i to n-1. For each j, add nums[j] to the map and increase its frequency.
Step 4. Check if the current subarray has exactly k distinct elements
You can check this by using freq.size(), which gives the number of unique keys (i.e., distinct elements) in the subarray.
Step 5. Return the final count
After all subarrays have been checked, return the answer.
Subarrays with K Different Integers Example
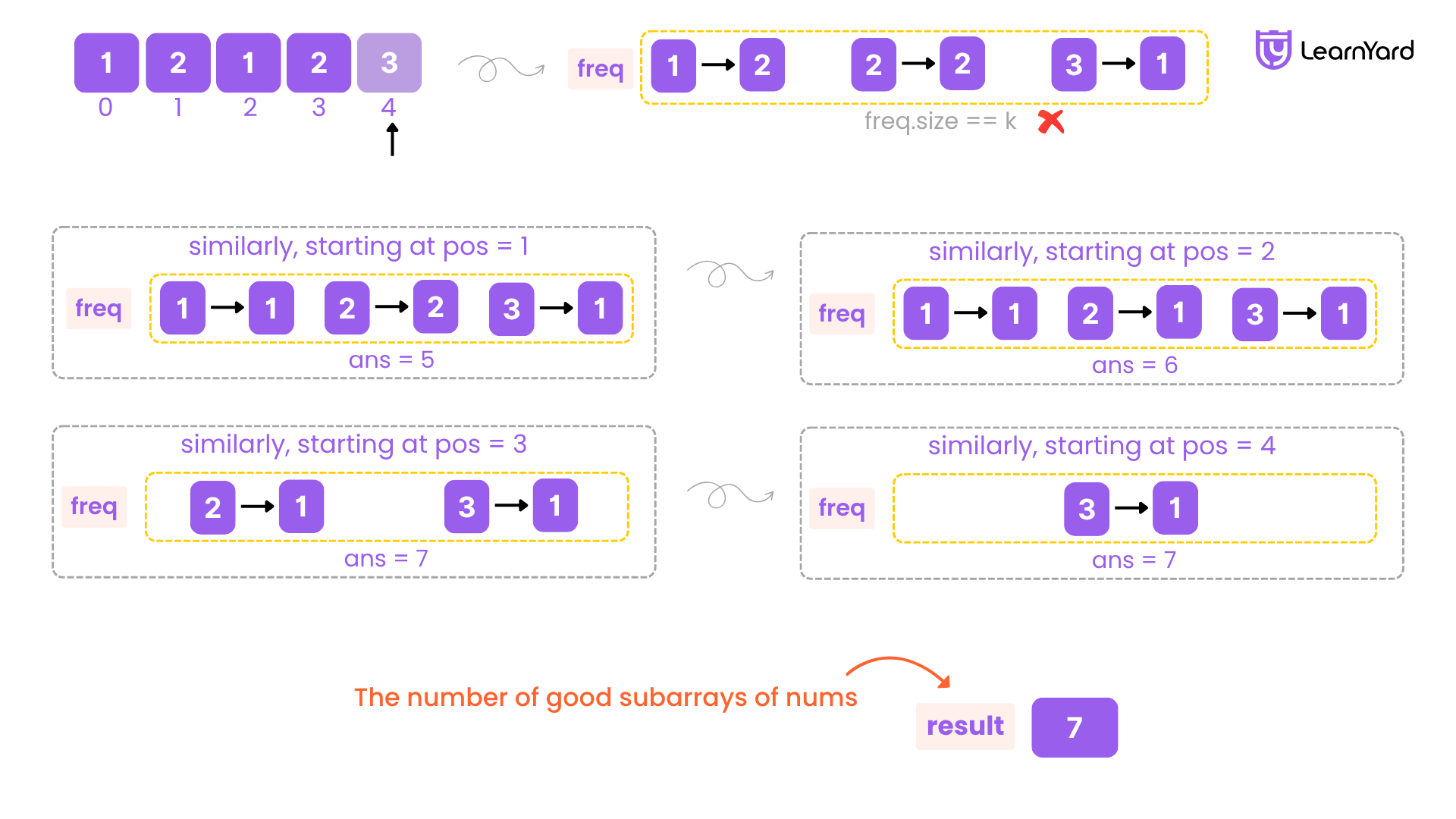
Input: nums = [1,2,2,1], k = 2
Output: 5
Explanation: Subarrays formed with exactly 2 different integers: [1,2], [1, 2, 2], [1,2, 2, 1], [2,2,1], [2,1]
- n = 4 (array length)
- k = 2 (want subarrays with exactly 2 distinct elements)
- nums = [1, 2, 2, 1]
Function Behavior Recap
The function loops over all subarrays nums[i..j], uses a map freq to track the frequency of elements, and increments ans whenever the number of distinct keys in the map is exactly k.
Step-by-Step Dry Run
Let’s go through each pair of (i, j):
i = 0
- freq = {}
- j = 0: freq = {1:1} → distinct = 1 → No
- j = 1: freq = {1:1, 2:1 → distinct = 2 → Yes count = 1
- j = 2: freq = {1:1, 2:2} → distinct = 2 → Yes count = 2
- j = 3: freq = {1:2, 2:2} → distinct = 2 → Yes count = 3
✔ Total count = 3
i = 1
- freq = {}
- j = 1: freq = {2:1} → distinct = 1 → No
- j = 2: freq = {2:2} → distinct = 1 → No
- j = 3: freq = {2:2, 1:1} → distinct = 2 → Yes count = 4
✔ Total count = 4
i = 2
- freq = {}
- j = 2: freq = {2:1} → distinct = 1 → No
- j = 3: freq = {2:1, 1:1} → distinct = 2 → Yes count = 5
✔ Total count = 5
i = 3
- freq = {}
- j = 3: freq = {1:1} → distinct = 1 → No
✔ Total count remains = 5
Final Output: 5
Subarrays with K Different Integers Solution
Subarrays with K Different Integers Solution in C++
int subarraysWithKDistinct(vector<int>& nums, int k) {
// Get the size of the array
int n = nums.size();
// Initialize answer to 0
int ans = 0;
// Map to store frequency of elements in current subarray
map<int, int> freq;
// Try every possible starting index for subarray
for(int i = 0; i < n; ++i) {
// Clear the frequency map for new starting index
freq.clear();
// Try every possible ending index for subarray starting at i
for(int j = i; j < n; ++j) {
// Increment the count of nums[j] in the frequency map
freq[nums[j]]++;
// If the number of distinct integers in current subarray is exactly k
if(freq.size() == k) {
// Increment the answer
ans++;
}
}
}
// Return the total count
return ans;
}Subarrays with K Different Integers Solution in Java
class Solution {
// Function to count subarrays with exactly K distinct integers
public static int subarraysWithKDistinct(int[] nums, int k) {
// Get the size of the array
int n = nums.length;
// Initialize answer to 0
int ans = 0;
// Map to store frequency of elements
Map<Integer, Integer> freq = new HashMap<>();
// Try every possible starting index for subarray
for (int i = 0; i < n; ++i) {
// Clear the frequency map for new starting index
freq.clear();
// Try every possible ending index for subarray starting at i
for (int j = i; j < n; ++j) {
// Increment count for nums[j]
freq.put(nums[j], freq.getOrDefault(nums[j], 0) + 1);
// If the number of distinct integers is exactly k
if (freq.size() == k) {
// Increment the answer
ans++;
}
}
}
// Return the total count
return ans;
}
}Subarrays with K Different Integers Solution in Python
class Solution:
def subarraysWithKDistinct(self, nums: List[int], k: int) -> int:
# Get the size of the array
n = len(nums)
# Initialize answer to 0
ans = 0
# Try every possible starting index for subarray
for i in range(n):
# Dictionary to store frequency of elements
freq = {}
# Try every possible ending index for subarray starting at i
for j in range(i, n):
# Increment count for nums[j]
freq[nums[j]] = freq.get(nums[j], 0) + 1
# If the number of distinct integers is exactly k
if len(freq) == k:
# Increment the answer
ans += 1
# Return the total count
return ansSubarrays with K Different Integers Solution in Javascript
/**
* @param {number[]} nums
* @param {number} k
* @return {number}
*/
var subarraysWithKDistinct = function(nums, k) {
// Get the size of the array
const n = nums.length;
// Initialize answer to 0
let ans = 0;
// Try every possible starting index for subarray
for (let i = 0; i < n; ++i) {
// Map to store frequency of elements
const freq = new Map();
// Try every possible ending index for subarray starting at i
for (let j = i; j < n; ++j) {
// Increment count for nums[j]
freq.set(nums[j], (freq.get(nums[j]) || 0) + 1);
// If the number of distinct integers is exactly k
if (freq.size === k) {
// Increment the answer
ans++;
}
}
}
// Return the total count
return ans;
};
Subarrays with K Different Integers Complexity Analysis
Time Complexity: O(n2 log n)
Outer Loop: for i = 0 to n - 1
- Runs n times
Inner Loop: for j = i to n - 1
- In worst case, runs n - i times
- Over all i, this gives O(n²) total iterations
Inside Inner Loop:
- freq is a std::map<int, int> → typically implemented as a balanced BST (like Red-Black Tree)
- Inserting or updating a key (freq[nums[j]]++) is O(log D) time, where D is the number of distinct elements in the subarray so far (at most n)
- freq.size() is constant time, since the map maintains size
So each inner iteration does O(log n) work in the worst case (when all elements are distinct).
Final Time Complexity
We do:
- O(n²) iterations total
- Each iteration does O(log n) operations on the map
Overall Time Complexity: O(n² * log n)
Space Complexity: O(n)
Auxiliary Space Complexity:
Auxiliary space refers to the extra memory used by the algorithm, excluding input and output.
In this brute-force solution:
- A map<int, int> freq is used to store the frequency of elements in the current subarray.
In the worst case, if all elements in a subarray are distinct, the map can grow to contain up to n entries (where n is the size of the input array). So, this takes O(n) space. - Aside from that, only a few scalar variables like i, j, n, and ans are used, which consume constant space O(1).
Auxiliary space complexity is O(n).
Total Space Complexity:
- Input space: The input vector nums contains n elements. Although passed by reference, the input still occupies O(n) space.
- Output space: The output is a single integer (ans), which uses O(1) space.
- Auxiliary space: As explained above, the map freq can take up to O(n) space in the worst case.
So, total space = input + output + auxiliary =
O(n) + O(1) + O(n) = O(n) (since O(n) dominates)
Total space complexity is O(n).
Is the Brute Force Approach Efficient?
The brute-force approach, while easy to understand and implement, is not efficient for larger inputs.
According to the problem constraints:
- The size of the array can be as large as 2 × 10⁴
- Each number in the array and the value of k can go up to n (the length of the array)
In the brute-force method, we go through every possible subarray, and for each one, we use a map to count unique elements. This results in a time complexity of O(n² × log n) in the worst case, which becomes extremely slow when n is around 20,000.
So while this approach might work for small arrays, it will time out or perform poorly for large inputs. That’s why we need to optimize the solution to handle bigger test cases within the time limits.
To optimize our solution, we can’t afford to visit every possible subarray that alone takes O(n²) time, which is too slow for large input sizes.
We need to do better than brute force by finding a smarter way to count subarrays with exactly k distinct elements without checking all of them one by one.
Let’s now explore how we can approach this more efficiently in the optimal solution.
Optimal Approach
Intuition
Let’s take a moment to understand what we’re trying to find here.
We need to count all the subarrays that have exactly k distinct elements.
Now, doing this directly can be a bit tricky. So instead, let’s make the problem a little easier by changing it slightly:
What if we count all the subarrays that have less than or equal to k distinct elements?
This version of the problem is simpler to solve. And here's the key idea:
If we count all the subarrays with at most k distinct elements, that includes:
- Subarrays with exactly k distinct elements
- Subarrays with exactly k - 1 distinct elements
- Subarrays with exactly k - 2, k - 3, and so on, all the way down to 1 distinct element.
Now suppose, if we also find the count of subarrays with unique elements less than or equal to k-1. Then it will contain the following subarrays.
- Subarrays with exactly k - 1
- Subarrays with exactly k - 2, and so on, down to 1
Do you see what we can do here?
If we subtract the second count (at most k - 1) from the first count (at most k). We’ll be left with only the subarrays that have exactly k distinct elements, the ones we actually care about.
Now all we need to do is we need to subtract the count of subarrays with distinct elements less than or equal to k-1 from the count of subarrays with distinct elements less than or equal to k.
So, the final formula becomes:
Subarrays with exactly k distinct elements = Subarrays with at most k distinct elements - Subarrays with at most (k - 1) distinct elements
How to Count the Subarrays with Distinct Elements Less Than or Equal to K?
To solve this subproblem, we can’t afford to go through every possible subarray. That would take too long and wouldn’t be efficient, especially for large arrays.
So let’s think about it a bit differently.
Imagine we fix an index i somewhere in the array. Our goal is to count all valid subarrays that end at index i.
By "valid", we mean subarrays that contain at most k distinct elements.
To do this efficiently, we can use a sliding window approach with two pointers, one for the start of the window (l) and one for the end (r).
We’ll also use a map (in C++) or a dictionary (in Python) to keep track of how many times each element appears in the current window.
- The key will be the element itself
- The value will be the frequency of the elements (i.e., how many times it appears).
Here’s how it works step by step:
- Start with both pointers, l and r at the beginning of the array.
- Move the r pointer one step at a time to include a new element into the window.
- For each new element added at r, update the map/dictionary to increase its frequency.
- If the number of distinct elements in the current window (i.e., the size of the map) becomes more than k, it means the window is invalid.
So we shrink the window from the left by moving l forward and decreasing the count of those elements in the map until the number of distinct elements becomes k or less again. - Once the window becomes valid again (i.e., it contains at most k distinct elements), we can count how many subarrays end at index r and are valid. These subarrays are:
- Starting at l and ending at r
- Starting at l + 1 and ending at r
- Starting at r and ending at r
- So, the number of such subarrays are: r - l + 1
- We add this number to our final answer because all these subarrays ending at r are valid.
- Then we move r forward and repeat the process until we reach the end of the array.
What is Sliding Window Technique?
Imagine you’re looking at a long line of items — like numbers in an array or letters in a string — and you want to examine small parts (subarrays or substrings) of it one at a time.
The Sliding Window Technique helps us do this efficiently, without starting over every time.
Instead of recalculating everything from scratch for each part, we slide a “window” over the data, reusing most of the previous work.
What is a “Window”?
A window is just a small segment or a range within the array or string.
For example:
Let’s say we have this array: arr = [1, 2, 3, 4, 5, 6]
If we want to look at subarrays of size 3:
- First window: [1, 2, 3]
- Next window: [2, 3, 4]
- Then: [3, 4, 5], and so on...
Each time, we just move the window one step forward, dropping the first element and including the next.
Why Do We Use It?
Because it's efficient!
Let’s say we wanted the sum of each window of size 3:
Naive Way (Brute Force):
- For every window, loop through the 3 elements and sum them → O(n * k), where n = length of array, k = window size.
Sliding Window Way:
Sum the first window once. For the next window:
- Subtract the element going out of the window.
- Add the element coming in.
This makes each new window sum in O(1) time → total O(n).
Types of Sliding Windows
There are mainly two types:
1. Fixed-size Sliding Window - Window size stays the same.
2. Variable-size Sliding Window - The window grows or shrinks based on conditions.
In this problem, we are using fixed size Sliding Window as the window size if fixed, i.e. length of p.
Subarrays with K Different Integers Algorithm
Step 1: Create the Helper Function (countAtMostK)
Write a separate function to count the number of subarrays that contain at most k distinct elements. This will use the sliding window approach.
Step 2: Prepare for the Sliding Window
Inside the helper function:
- Get the size of the array.
- Set up a map (or dictionary) to track the frequency of elements in the current window.
- Initialise two pointers, l (left) and r (right), to represent the sliding window.
- Also, initialise a variable to keep track of the total valid subarrays found.
Step 3: Slide the Right Pointer
Loop through the array using the right pointer r. At each step, add the current element to the frequency map and update its count.
Step 4: Shrink the Window if Needed
If the number of distinct elements in the window (i.e., the size of the map) becomes greater than k, shrink the window from the left by moving the l pointer forward. Decrease the frequency of the leftmost element, and if its count becomes zero, remove it from the map.
Step 5: Count Valid Subarrays
After making sure the window has at most k distinct elements, add the number of valid subarrays ending at index r (which is r - l + 1) to your answer.
Step 6: Repeat Until the End of the Array
Continue moving the r pointer and repeat steps 3 to 5 until the end of the array is reached.
Step 7: Return the Result
Once the loop ends, return the final count of subarrays with less than or equal to k distinct elements from the helper function.
Step 9: Compute Final Answer
Back in the main function, subtract the result of countAtMostK(k - 1) from countAtMostK(k) to get the number of subarrays with exactly k distinct elements, and return it.
Animation of Subarrays with K Different Integers - Optimal Approach
Subarrays with K Different Integers Example
Input: nums = [1,2,2,1], k = 2
Output: 5
Explanation: Subarrays formed with exactly 2 different integers: [1,2], [1, 2, 2], [1,2, 2, 1], [2,2,1], [2,1]
- nums = [1, 2, 2, 1]
- k = 2
The main idea of this code:
result = countAtMostK(nums, k) - countAtMostK(nums, k - 1)
So we will compute:
- countAtMostK(nums, 2) → count of subarrays with at most 2 distinct elements
- countAtMostK(nums, 1) → count of subarrays with at most 1 distinct element
- Subtract the two to get exactly 2 distinct elements
Step 1: countAtMostK(nums, 2)
Let’s do a dry run of this using a sliding window
We’ll use:
- mp to store counts of elements
- Two pointers: l (left), r (right)
Initial values:
- l = 0, r = 0, ans = 0, mp = {}
r = 0
- Add 1: mp = {1:1}
- size = 1 (≤ 2) → Yes
- Add r - l + 1 = 1 → ans = 1
r = 1
- Add 2: mp = {1:1, 2:1}
- size = 2 (≤ 2) → Yes
- Add r - l + 1 = 2 → ans = 3
r = 2
- Add 2: mp = {1:1, 2:2}
- size = 2 → Yes
- Add r - l + 1 = 3 → ans = 6
r = 3
- Add 1: mp = {1:2, 2:2}
- size = 2 → Yes
- Add r - l + 1 = 4 → ans = 10
Done — countAtMostK(nums, 2) = 10
Step 2: countAtMostK(nums, 1)
Reset:
- l = 0, r = 0, ans = 0, mp = {}
r = 0
- Add 1: mp = {1:1}
- size = 1 → Yes
- Add 1 → ans = 1
r = 1
- Add 2: mp = {1:1, 2:1}
- size = 2 (> 1) → No shrink from left
- Remove 1: mp = {2:1}
- l = 1
- Add r - l + 1 = 1 → ans = 2
r = 2
- Add 2: mp = {2:2}
- size = 1 → Yes
- Add r - l + 1 = 2 → ans = 4
r = 3
- Add 1: mp = {2:2, 1:1}
- size = 2 → No shrink
- Remove 2: mp = {2:1, 1:1} → still 2
- l = 2
- Remove 2: mp = {1:1}
- l = 3
- size = 1 → Yes
- Add r - l + 1 = 1 → ans = 5
Done — countAtMostK(nums, 1) = 5
Final Calculation: subarraysWithKDistinct(nums, 2) = 10 - 5 = 5
Subarrays with K Different Integers leetcode Solution
Subarrays with K Different Integers solution in C++
class Solution {
public:
int subarraysWithKDistinct(vector<int>& nums, int k) {
// Use the helper function: atMostK for k and k-1, and return their difference
return countAtMostK(nums, k) - countAtMostK(nums, k - 1);
}
// Function to count subarrays with at most K distinct integers
int countAtMostK(vector<int>& nums, int k) {
// Get the size of the array
int n = nums.size();
// Map to store frequency of elements in the current window
map<int, int> mp;
// Initialize left and right pointers for window
int l = 0, r = 0;
// Initialize answer to 0
int ans = 0;
// Move the right pointer through the array
while (r < n) {
// Add nums[r] to the frequency map
mp[nums[r]]++;
// If we have more than k distinct elements, shrink the window from the left
while (mp.size() > k) {
mp[nums[l]]--;
// If the count of nums[l] is zero, remove it from the map
if (mp[nums[l]] == 0) mp.erase(nums[l]);
// Move the left pointer to the right
l++;
}
// Add the number of subarrays ending at r and starting from l to r
ans += r - l + 1;
// Move the right pointer to the right
r++;
}
// Return the total count
return ans;
}
};Subarrays with K Different Integers solution in Java
class Solution {
public int subarraysWithKDistinct(int[] nums, int k) {
// Use the helper function: atMostK for k and k-1, and return their difference
return countAtMostK(nums, k) - countAtMostK(nums, k - 1);
}
// Function to count subarrays with at most K distinct integers
public int countAtMostK(int[] nums, int k) {
// Get the size of the array
int n = nums.length;
// Map to store frequency of elements in the current window
Map<Integer, Integer> mp = new HashMap<>();
// Initialize left and right pointers for window
int l = 0, r = 0;
// Initialize answer to 0
int ans = 0;
// Move the right pointer through the array
while (r < n) {
// Add nums[r] to the frequency map
mp.put(nums[r], mp.getOrDefault(nums[r], 0) + 1);
// If we have more than k distinct elements, shrink the window from the left
while (mp.size() > k) {
mp.put(nums[l], mp.get(nums[l]) - 1);
// If the count of nums[l] is zero, remove it from the map
if (mp.get(nums[l]) == 0) mp.remove(nums[l]);
// Move the left pointer to the right
l++;
}
// Add the number of subarrays ending at r and starting from l to r
ans += r - l + 1;
// Move the right pointer to the right
r++;
}
// Return the total count
return ans;
}
}Subarrays with K Different Integers solution in Python
class Solution:
def subarraysWithKDistinct(self, nums: List[int], k: int) -> int:
# Use the helper function: atMostK for k and k-1, and return their difference
return self.countAtMostK(nums, k) - self.countAtMostK(nums, k - 1)
# Function to count subarrays with at most K distinct integers
def countAtMostK(self, nums: List[int], k: int) -> int:
# Get the size of the array
n = len(nums)
# Dictionary to store frequency of elements in the current window
freq = {}
# Initialize left pointer for window
l = 0
# Initialize answer to 0
ans = 0
# Move the right pointer through the array
for r in range(n):
# Add nums[r] to the frequency dictionary
freq[nums[r]] = freq.get(nums[r], 0) + 1
# If we have more than k distinct elements, shrink the window from the left
while len(freq) > k:
freq[nums[l]] -= 1
# If the count of nums[l] is zero, remove it from the dictionary
if freq[nums[l]] == 0:
del freq[nums[l]]
# Move the left pointer to the right
l += 1
# Add the number of subarrays ending at r and starting from l to r
ans += r - l + 1
# Return the total count
return ansSubarrays with K Different Integers solution in Javascript
/**
* @param {number[]} nums
* @param {number} k
* @return {number}
*/
var subarraysWithKDistinct = function(nums, k) {
// Return the difference between atMostK for k and k-1
return countAtMostK(nums, k) - countAtMostK(nums, k - 1);
// Function to count subarrays with at most K distinct integers
function countAtMostK(nums, k) {
// Get the size of the array
const n = nums.length;
// Map to store frequency of elements in the current window
const freq = new Map();
// Initialize left pointer for window
let l = 0;
// Initialize answer to 0
let ans = 0;
// Move the right pointer through the array
for (let r = 0; r < n; ++r) {
// Add nums[r] to the frequency map
freq.set(nums[r], (freq.get(nums[r]) || 0) + 1);
// If we have more than k distinct elements, shrink the window from the left
while (freq.size > k) {
freq.set(nums[l], freq.get(nums[l]) - 1);
// If the count of nums[l] is zero, remove it from the map
if (freq.get(nums[l]) === 0) freq.delete(nums[l]);
// Move the left pointer to the right
l++;
}
// Add the number of subarrays ending at r and starting from l to r
ans += r - l + 1;
}
// Return the total count
return ans;
}
};Subarrays with K Different Integers Complexity Analysis
Time Complexity: O(n logn)
1. Function countAtMostK(nums, k)
This function uses the sliding window technique, where:
- r goes from 0 to n - 1
- l only moves forward when the distinct count exceeds k
- The key insight: both l and r move at most n times
So, the entire while loop runs in O(n) time.
Each operation inside the loop involves:
- Inserting or deleting from map<int, in> → takes O(log n) time (because std::map is implemented as a balanced BST)
Thus, each step takes O(log n) time, and there are O(n) steps → overall time:
O(n × log n)
2. Main Function subarraysWithKDistinct
It calls countAtMostK(nums, k) and countAtMostK(nums, k - 1), each of which runs in O(n × log n) time.
So:
Total Time Complexity = O(n × log n) + O(n × log n) = O(n × log n)
Space Complexity: O(n)
Auxiliary Space Complexity:
This refers to all extra memory used by the algorithm (excluding input and output).
In the optimal solution:
- A map<int, int> (or unordered_map if used instead) is maintained to store the frequency of elements in the current sliding window.
- In the worst case, if all elements in the array are distinct, the map will store up to n elements.
- So, the frequency map takes O(n) space.
- Other variables (l, r, ans, loop counters) are scalar values and use O(1) space.
So, auxiliary space complexity = O(n).
Total Space Complexity:
Total space includes:
- Input space: the array nums, which contains n elements → O(n)
- Output space: a single integer result → O(1)
- Auxiliary space: from above → O(n)
Combining these:
Total Space = Input + Output + Auxiliary = O(n) + O(1) + O(n) = O(n)
Similar Problems
Now we have successfully tackled this problem, let's try these similar problems:-
Given a string s, find the length of the longest substring without duplicate characters.
A substring is a contiguous (non-empty) sequence of characters within a string.
A vowel substring is a substring that only consists of vowels ('a', 'e', 'i', 'o', and 'u') and has all five vowels present in it.
Given a string word, return the number of vowel substrings in word.
Given an integer array nums and two integers k and p, return the number of distinct subarrays, which have at most k elements that are divisible by p.
Two arrays nums1 and nums2 are said to be distinct if:
- They are of different lengths, or
- There exists at least one index i where nums1[i] != nums2[i].
A subarray is defined as a non-empty contiguous sequence of elements in an array.
You are given an array nums consisting of positive integers.
We call a subarray of an array complete if the following condition is satisfied:
- The number of distinct elements in the subarray is equal to the number of distinct elements in the whole array.
Return the number of complete subarrays.
A subarray is a contiguous non-empty part of an array.