Split Array Largest Sum Solution In C++/Java/Python/JS
Split array largest sum Problem Description:
Given an integer array nums and an integer k, split nums into k non-empty subarrays such that the largest sum of any subarray is minimized.
Return the minimized largest sum of the split.
A subarray is a contiguous part of the array.
Examples:
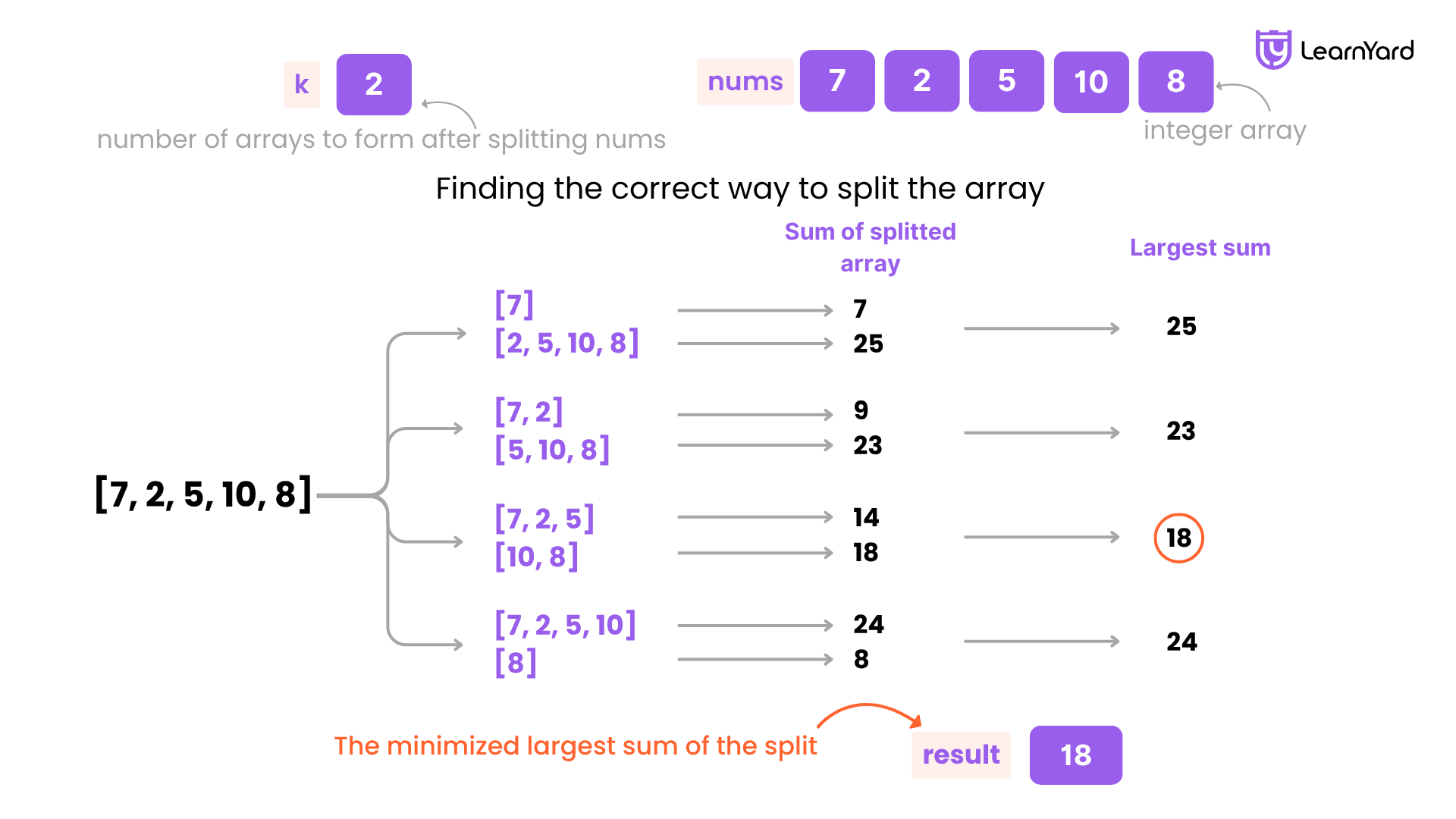
Input: nums = [7,2,5,10,8], k = 2
Output: 18
Explanation: There are four ways to split nums into two subarrays.
The best way is to split it into [7,2,5] and [10,8], where the largest sum among the two subarrays is only 18.
Input: nums = [1,2,3,4,5], k = 2
Output: 9
Explanation: There are four ways to split nums into two subarrays.
The best way is to split it into [1,2,3] and [4,5], where the largest sum among the two subarrays is only 9.
Constraints:
1 <= nums.length <= 1000
0 <= nums[i] <= 10⁶
1 <= k <= min(50, nums.length)
Brute Force Approach
To approach the problem, we are given an integer array nums and an integer k, and we need to determine the minimum largest sum required to split the array into k non-empty subarrays. Our goal is to find the smallest possible largest sum such that the array can be split into k valid subarrays.
What can be the minimum largest sum needed?
The minimum largest sum required should be the maximum element in the array, i.e., if we create subarrays such that each one contains only one element, the largest sum will be the maximum element in the array.
What would be the maximum largest sum?
The maximum largest sum should be the sum of all elements in the array. This is because, in the worst case, the entire array forms a single subarray, making the total sum the maximum possible largest sum.
Thus, our search space for the answer ranges from max(nums) to sum(nums). Now, the problem reduces to finding the minimum largest sum that allows us to split the array into k subarrays.
A basic approach is to iterate through all possible largest sums from max(nums) to sum(nums) and check whether the array can be split into k valid subarrays with that largest sum. If it is possible, then it is a valid solution; otherwise, we increase the largest sum and check again. We continue this process until we find the smallest valid largest sum.
Since the range from max(nums) to sum(nums) covers all possible largest sums, starting from the smallest and stopping at the first valid largest sum will give us the desired result.
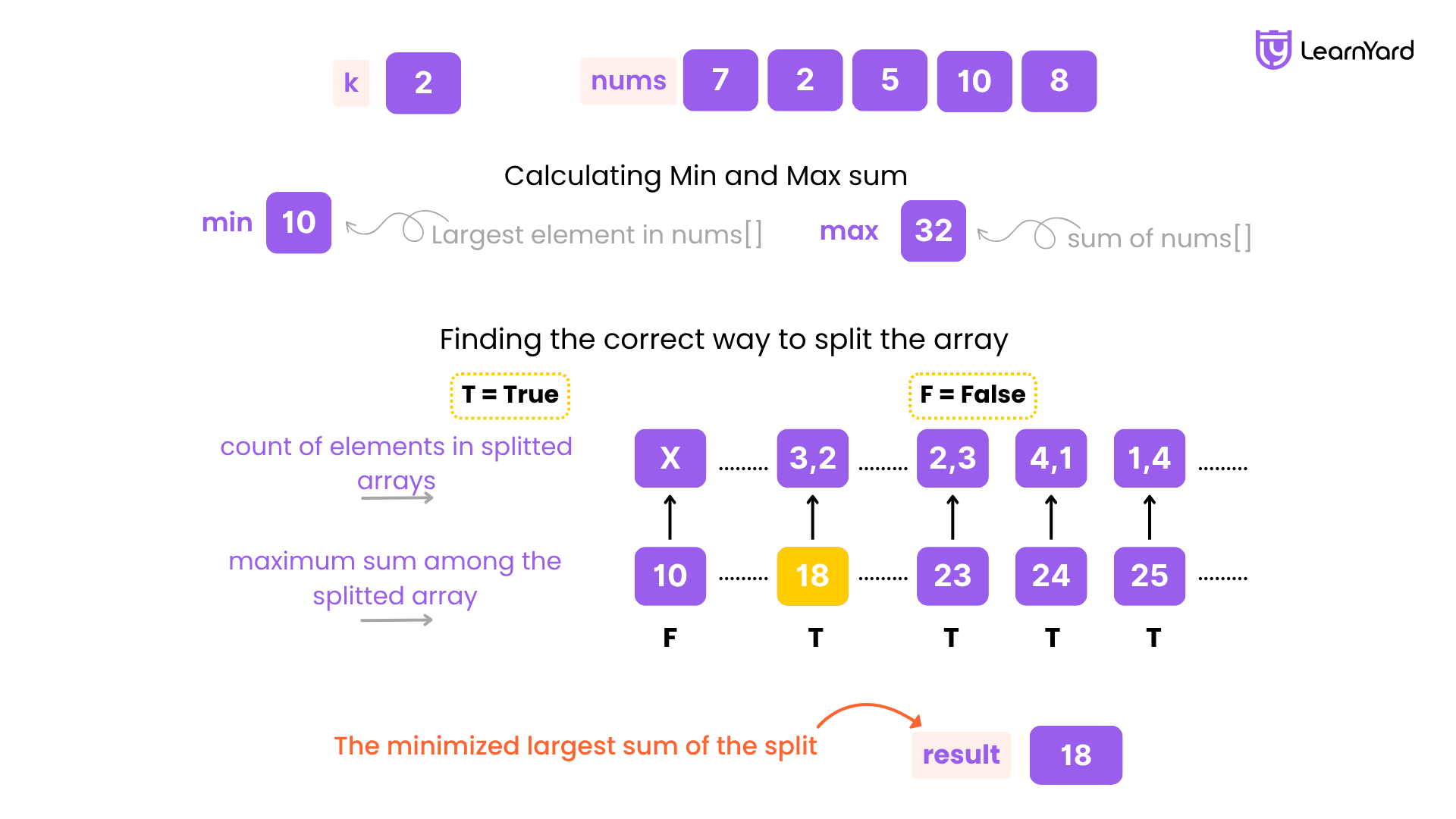
Consider the example with nums = [7,2,5,10,8] and k = 2. We start by taking the smallest possible largest sum, which is 10 (the maximum element), and the largest possible largest sum, which is 32 (the total sum). We then check whether the array can be split into valid subarrays at each of these values:
- For largest sum = 10, we cannot create k valid subarrays. This doesn't work.
- For largest sum = 18, the array can be split into [7,2,5] and [10,8], making 18 the minimized largest sum that meets the condition.
Since 18 is the smallest valid largest sum, it is the minimum required largest sum to split the array.
So, the answer is 18.
Let's call the smallest largest sum needed to split the array as minLargestSum. Any value between max(nums) and minLargestSum - 1 won't work because it will always leave some subarrays exceeding the limit. However, any value from minLargestSum to sum(nums) will allow us to split the array correctly.
Therefore, minLargestSum is the smallest required largest sum to split the array into k subarrays, and we return minLargestSum as the answer.
How Can We Determine if a Given Largest Sum is Valid (Real World Example)?
Imagine you have an array of integers, and your goal is to determine if you can split the array into k subarrays where no subarray's sum exceeds the given largest sum. To achieve this, we simulate the process of checking whether all subarrays can be created with a specific largest sum.
Imagine you're moving through the array, tracking the current subarray sum. If the current subarray sum exceeds the given largest sum, you start a new subarray. You keep counting the number of subarrays formed in this way.
Steps to Check Validity:
- Start with count = 1 (one subarray already exists).
- Traverse the array and keep adding elements to the current subarray sum.
- If adding the next element causes the current subarray sum to exceed the given largest sum, start a new subarray and increment the count.
- If at any point the number of subarrays exceeds k, the given largest sum is too small, and we return false.
- If we successfully split the array into k subarrays, the given largest sum is valid, and we return true.
If all subarrays are created successfully, we return true → The largest sum is valid. If more than k subarrays are required, we return false → The largest sum is too small, and we need to increase it.
Why Does cnt ≤ k Always Lead to the Correct Answer?
If the number of subarrays formed (cnt) is less than or equal to k, it means we managed to split the array using fewer or exactly the required number of subarrays while satisfying the maximum subarray sum condition. This is optimal because:
- If cnt == k, we achieved the required split directly — perfect condition.
- If cnt < k, we technically have spare subarrays available, which means the chosen maximum subarray sum was sufficient to accommodate elements efficiently without excessive splits.
Since reducing the largest sum further would risk violating the conditions, stopping when cnt ≤ k ensures the minimum valid maximum sum is identified correctly.
Another possible approach to solve this problem could have been using the prefix sum technique.
This method follows a greedy strategy, where we make local decisions at each step to minimize the largest subarray sum. By sequentially adding elements until we exceed the allowed limit, we attempt to form subarrays as efficiently as possible. This greedy approach ensures that no element is left behind and each subarray maintains the required properties, eventually leading to the optimal solution.
The prefix sum array allows us to efficiently compute the sum of any subarray in constant time by leveraging the cumulative sums.
Using this, we could potentially determine valid subarray splits by tracking the difference between prefix sums at various points. However, this method becomes challenging in this context because prefix sums alone don't efficiently help in determining optimal subarray partitions within the given constraints.
The challenge lies in dynamically tracking the number of partitions required and ensuring the maximum subarray sum remains minimal. As a result, the binary search approach with the "valid check" method proves to be more efficient and direct in achieving the desired outcome.
Let's understand with an example:
Split Array Largest Sum Example:
Dry Run for Input: nums = [1, 2, 3, 4, 5], k = 2
Step 1: Identify the Search Space
- Minimum Possible Largest Sum: max(nums) = 5
- Maximum Possible Largest Sum: sum(nums) = 15
So, our search range is [5, 15].
Step 2: Brute Force Search
We'll test each possible maximum subarray sum in this range.
Checking for Maximum Subarray Sum = 5:
- Split: [1,2], [3], [4], [5] → 4 splits → Doesn't satisfy k = 2
Checking for Maximum Subarray Sum = 6:
- Split: [1, 2,3], [4], [5] → 3 splits → Doesn't satisfy k = 2
Checking for Maximum Subarray Sum = 7:
- Split: [1, 2, 3], [4], [5] → 3 splits → Doesn't satisfy k = 2
Checking for Maximum Subarray Sum = 8:
- Split: [1, 2, 3], [4], [5] → 3 splits → Doesn't satisfy k = 2
Checking for Maximum Subarray Sum = 9:
- Split: [1, 2, 3], [4, 5] → 2 splits → Satisfies k = 2
Step 3: Final Answer
The smallest valid maximum sum that meets the condition is 9.
Steps to Implement the Solution:
- Understand the Problem Statement
- Goal: Split the array into k subarrays such that the maximum subarray sum is minimized.
- Determine the Search Space
- Low = Maximum element in the array (minimum possible largest sum).
- High = Sum of all elements in the array (maximum possible largest sum).
- Implement the isValid() Function
- Initialize cnt = 1 (to track the number of subarrays).
- Maintain a running total for the current subarray.
- Iterate through the array:
- Add the current element to total.
- If total > mid, start a new subarray and reset total to the current element.
- Increment cnt and check if it exceeds k.
- If so, return false.
- Return true if the required conditions are met.
- Brute Force Search in splitArray()
- Loop from low to high:
- If isValid(nums, k, i) is true, store i as the answer and break the loop.
- Return the Final Answer
- The stored answer will be the minimized maximum subarray sum.
Split Array Largest Sum Leetcode Solution
Split array largest sum Leetcode Solution / Code Implementation
1. Split array largest sum solution in C++ Try on Compiler
class Solution {
// Function to check if a given maximum subarray sum (mid) is valid
bool isValid(vector<int> &nums, int k, int mid)
{
// Initialize the count of subarrays
int cnt = 1;
// Initialize the total sum of the current subarray
int total = 0;
// Iterate through each element in the array
for(auto &num : nums)
{
// Add the current element to the total
total += num;
// If the total exceeds the maximum allowed sum (mid)
if(total > mid)
{
// Start a new subarray with the current element
total = num;
// Increment the subarray count
cnt++;
// If the count exceeds the required number of subarrays
if(cnt > k)
return false;
}
}
// If valid, return true
return true;
}
public:
// Function to find the minimized largest sum of split subarrays
int splitArray(vector<int>& nums, int k) {
// Minimum possible maximum sum (max element in the array)
int low = *max_element(nums.begin(), nums.end());
// Maximum possible maximum sum (sum of all elements in the array)
int high = accumulate(nums.begin(), nums.end(), 0);
// Variable to store the answer
int ans = 0;
// Brute force search through all possible values from low to high
for(int i = low; i <= high; i++)
{
// If the current maximum sum is valid
if(isValid(nums, k, i))
{
// Store the answer and stop searching (minimum found)
ans = i;
break;
}
}
// Return the minimized largest sum
return ans;
}
};
2. Split array largest sum solution in Java Try on Compiler
class Solution {
// Function to check if a given maximum subarray sum (mid) is valid
private boolean isValid(int[] nums, int k, int mid) {
// Initialize the count of subarrays
int cnt = 1;
// Initialize the total sum of the current subarray
int total = 0;
// Iterate through each element in the array
for(int num : nums) {
// Add the current element to the total
total += num;
// If the total exceeds the maximum allowed sum (mid)
if(total > mid) {
// Start a new subarray with the current element
total = num;
// Increment the subarray count
cnt++;
// If the count exceeds the required number of subarrays
if(cnt > k)
return false;
}
}
// If valid, return true
return true;
}
// Function to find the minimized largest sum of split subarrays
public int splitArray(int[] nums, int k) {
// Minimum possible maximum sum (max element in the array)
int low = Arrays.stream(nums).max().getAsInt();
// Maximum possible maximum sum (sum of all elements in the array)
int high = Arrays.stream(nums).sum();
// Variable to store the answer
int ans = 0;
// Brute force search through all possible values from low to high
for(int i = low; i <= high; i++) {
// If the current maximum sum is valid
if(isValid(nums, k, i)) {
// Store the answer and stop searching (minimum found)
ans = i;
break;
}
}
// Return the minimized largest sum
return ans;
}
}
3. Split array largest sum solution in Python Try on Compiler
class Solution:
# Function to check if a given maximum subarray sum (mid) is valid
def isValid(self, nums, k, mid):
# Initialize the count of subarrays
cnt = 1
# Initialize the total sum of the current subarray
total = 0
# Iterate through each element in the array
for num in nums:
# Add the current element to the total
total += num
# If the total exceeds the maximum allowed sum (mid)
if total > mid:
# Start a new subarray with the current element
total = num
# Increment the subarray count
cnt += 1
# If the count exceeds the required number of subarrays
if cnt > k:
return False
# If valid, return True
return True
# Function to find the minimized largest sum of split subarrays
def splitArray(self, nums, k):
# Minimum possible maximum sum (max element in the array)
low = max(nums)
# Maximum possible maximum sum (sum of all elements in the array)
high = sum(nums)
# Variable to store the answer
ans = 0
# Brute force search through all possible values from low to high
for i in range(low, high + 1):
# If the current maximum sum is valid
if self.isValid(nums, k, i):
# Store the answer and stop searching (minimum found)
ans = i
break
# Return the minimized largest sum
return ans
4. Split array largest sum solution in Javascript Try on Compiler
/**
* Function to check if a given maximum subarray sum (mid) is valid
* @param {number[]} nums - The input array
* @param {number} k - The number of required subarrays
* @param {number} mid - The maximum possible subarray sum being checked
* @return {boolean} - True if valid, otherwise false
*/
function isValid(nums, k, mid) {
// Initialize the count of subarrays
let cnt = 1;
// Initialize the total sum of the current subarray
let total = 0;
// Iterate through each element in the array
for(let num of nums) {
// Add the current element to the total
total += num;
// If the total exceeds the maximum allowed sum (mid)
if(total > mid) {
// Start a new subarray with the current element
total = num;
// Increment the subarray count
cnt++;
// If the count exceeds the required number of subarrays
if(cnt > k)
return false;
}
}
// If valid, return true
return true;
}
/**
* Function to find the minimized largest sum of split subarrays
* @param {number[]} nums - The input array
* @param {number} k - The number of required subarrays
* @return {number} - The minimized largest sum of split subarrays
*/
var splitArray = function(nums, k) {
// Minimum possible maximum sum (max element in the array)
let low = Math.max(...nums);
// Maximum possible maximum sum (sum of all elements in the array)
let high = nums.reduce((a, b) => a + b, 0);
// Variable to store the answer
let ans = 0;
// Brute force search through all possible values from low to high
for(let i = low; i <= high; i++) {
// If the current maximum sum is valid
if(isValid(nums, k, i)) {
// Store the answer and stop searching (minimum found)
ans = i;
break;
}
}
// Return the minimized largest sum
return ans;
};
Split array largest sum Complexity Analysis (Brute Force)
Time Complexity: O(sum(nums) × n)
The given code uses a brute force approach to find the minimized largest sum for the split subarrays. Let's analyze its complexity step by step.
1: Identifying the Range of Possible Answers
- The search space ranges from low = max(nums) to high = sum(nums).
- In the worst case, the difference between these two values can be:
Range Size = sum(nums) - max(nums)
2: Checking Each Value in the Range
- For each value in the range, the code checks if that value is a valid maximum sum using the isValid function.
- The isValid function iterates through the entire array once, which is O(n).
Final Complexity
- The outer loop iterates from low to high, which in the worst case is O(sum(nums)).
- Each iteration calls the isValid function, which takes O(n).
Overall Time Complexity: O(sum(nums) × n)
Space Complexity: O(n)
- Auxiliary Space Complexity: O(1)
The algorithm uses only a few integer variables such as low, high, mid, ans, cnt, and total.
These are simple primitive variables that consume constant space.
No additional data structures (like arrays or hash maps) are created for computation.
Thus, the auxiliary space complexity is O(1). - Total Space Complexity: O(n)
The input array nums itself occupies O(n) space.
Apart from this, no additional data structures are created for calculations.
Since the space required is dominated by the input array, the total space complexity is O(n).
Will Brute Force Work Against the Given Constraints?
For the current solution, the time complexity is O(sum(nums) × n), where n is the number of elements in the array nums (1 ≤ nums.length ≤ 1000). In the worst-case scenario, the sum of the entire array can be as large as 10⁶ (since 0 ≤ nums[i] ≤ 10⁶), which leads to a time complexity of O(sum(nums) × n).
This can become inefficient because sum(nums) can be very large (1e6), making the solution impractical for many inputs, particularly when sum(nums) is close to its upper bound.
Given the constraints, with n up to 1000 and sum(nums) reaching up to 10⁶, the solution may not execute efficiently for a wide range of inputs, especially when sum(nums) is large. While it may work well for inputs with a smaller sum(nums), this time complexity does not guarantee that it will perform optimally for all cases.
In competitive programming environments, problems generally allow up to 10⁶ operations per test case. For most typical inputs, the solution might work fine, but in the worst-case scenario, the time complexity could exceed the limits. Optimizations are necessary to handle inputs where sum(nums) is large, making the solution more efficient and suitable for all possible cases.
How to optimize it?
In the previous approach, we looked at the minimum and maximum possible subarray sums and checked every possible sum in that range to find the smallest maximum subarray sum that satisfies the given condition. This gave us O(sum(nums) × n) time complexity, which was too slow and caused TLE (Time Limit Exceeded).
Now, let’s think about improving this.
The main issue was that we checked every possible sum from max(nums) to sum(nums), which took a lot of time.
Can we make this part faster?
Yes! Here’s the hint:
We are searching for the minimum possible largest sum that works, and we know it lies between max(nums) and sum(nums).
Now that we know the two endpoints, max(nums) and sum(nums), let's make a few observations:
- The data structure is sorted:
Although the array itself may not be sorted, we can still apply binary search logic because we are searching within a range of values — the range between the maximum element and the total sum. - The middle element helps minimize or maximize the search space:
If we take the middle value of the current range and check if it works (i.e., can we split the array into k subarrays such that no subarray has a sum greater than this middle value?), we can narrow the search space:
If it works, we move to the left half to find a smaller valid maximum subarray sum.
If it doesn’t work, we move to the right half to find a larger valid maximum subarray sum. - The search space is monotonic:
If a certain maximum subarray sum allows us to split the array into k subarrays, then any larger maximum subarray sum will also work.
If a certain maximum subarray sum does not allow us to split the array into k subarrays, then any smaller maximum subarray sum will also fail.
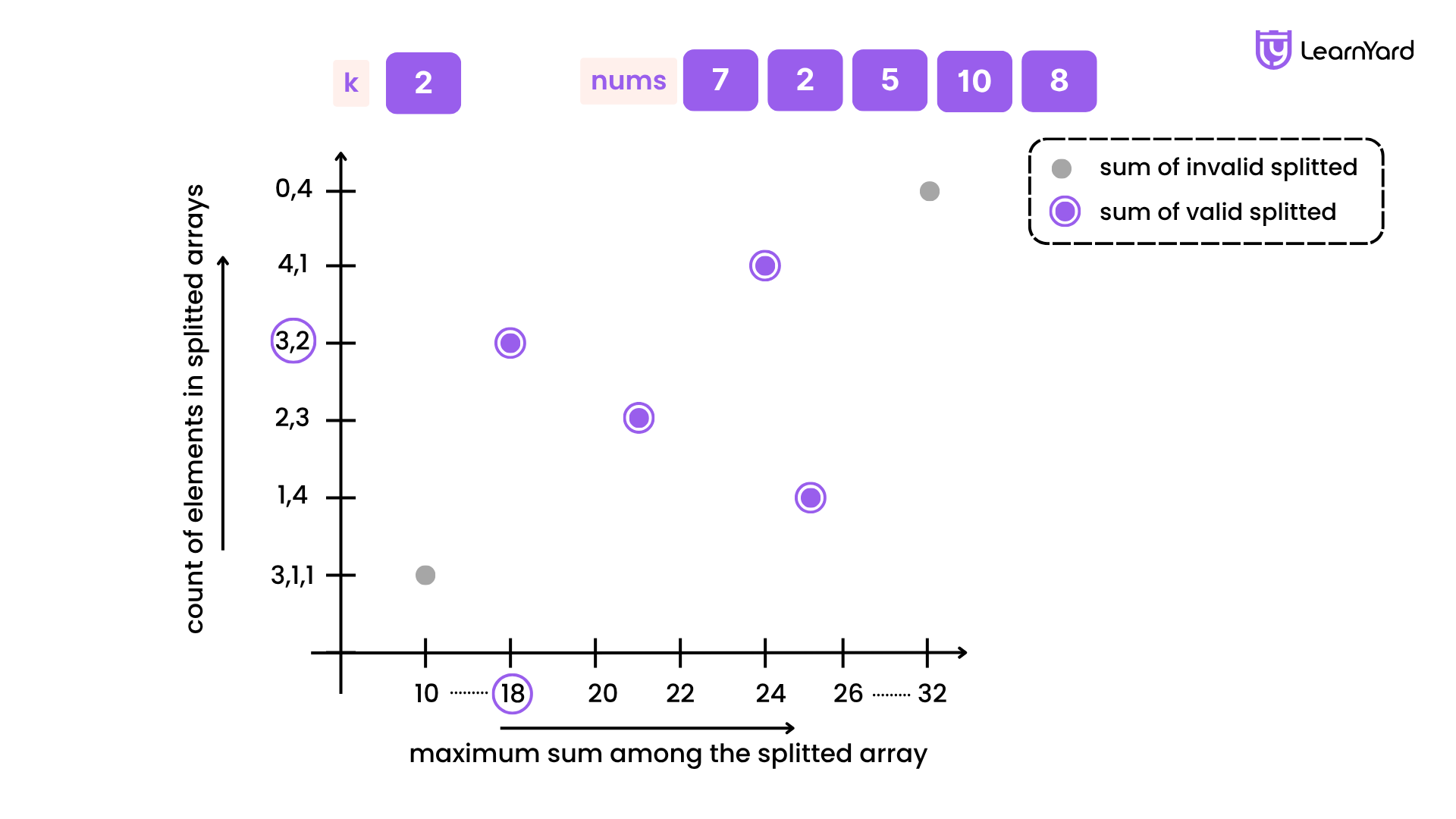
For example, with nums = [7, 2, 5, 10, 8] and k = 2, the algorithm will fail for a maximum subarray sum of 10, but starting from 18, the condition is satisfied.
This illustrates the monotonic property: once a certain maximum subarray sum works, any value larger than that will also work.
If we plot a graph with possible maximum subarray sums on the x-axis and whether we can split the array properly on the y-axis, we can observe the following:
- Before the minimum valid maximum subarray sum, we cannot split the array correctly.
- From the minimum valid maximum subarray sum onward, all larger values will also work.
Thus, the minimum valid maximum subarray sum represents the smallest possible value at which the array can be split correctly, and from that point forward, increasing the maximum sum remains feasible but unnecessary.
Instead of linearly checking all values from max(nums) to sum(nums), we can use binary search to efficiently determine the minimum valid maximum subarray sum.
Does this approach remind you of something you've seen before?
Yes, we are applying binary search here. By leveraging the sorted and monotonic properties of the possible subarray sums, we efficiently narrow down the search space to find the minimum maximum subarray sum that meets the condition, instead of checking each possible sum linearly.
Split array largest sum Binary Search Algorithm
Binary search can help us quickly find the minimum maximum subarray sum that meets the required conditions.
We can simply use binary search to determine the smallest possible largest sum when splitting the array into k subarrays.
Start by taking the middle value between low (the largest element in the array) and high (the sum of all elements in the array). If this mid value satisfies the condition that the array can be split into k or fewer subarrays with each subarray sum ≤ mid, we store it as a potential answer and narrow the search space to the left half, looking for a smaller valid maximum sum.
Otherwise, we move the search to the right half to find a larger valid maximum sum.
We continue this process as long as low ≤ high.
Once the condition breaks, the stored answer is returned as the minimum possible largest sum required. By using binary search, we can cut the search space in half at each step, which makes the solution much faster and avoids the TLE issue.
Let us understand this with a video.
Let's understand with an example:
Split Array Largest Sum Example:
Input: nums = [1, 2, 3, 4, 5], k = 2
Step 1: Identify the Search Space
- Minimum Possible Largest Sum: max(nums) = 5
- Maximum Possible Largest Sum: sum(nums) = 15
- Search range = [5, 15]
Step 2: Binary Search Process
Mid = (5 + 15) / 2 = 10
- Split: [1, 2, 3, 4], [5] → 2 subarrays → Valid
- Store 10 as a possible answer and try for a smaller value.
Mid = (5 + 9) / 2 = 7
- Split: [1, 2, 3], [4], [5] → 3 subarrays → Invalid
- Increase the search space to higher values.
Mid = (8 + 9) / 2 = 8
- Split: [1, 2, 3], [4, 5] → 2 subarrays → Valid
- Store 8 as a possible answer and try for a smaller value.
Mid = (8 + 7) / 2 = 9
- Split: [1, 2, 3], [4, 5] → 2 subarrays → Valid
- Store 9 as a possible answer and try for a smaller value.
Mid = 8 (Already checked)
Step 3: Final Answer
9 is the smallest possible largest sum that satisfies the condition.
How to code it up:
- Understand the Problem Statement
- You need to split the array into k subarrays such that the maximum sum among these subarrays is minimized.
- Identify the Search Space
- Low = Maximum element in the array (smallest possible valid maximum sum).
- High = Sum of all elements in the array (largest possible valid maximum sum).
- Implement the isValid() Function
- Initialize cnt = 1 (to count subarrays).
- Traverse the array and maintain a total that accumulates the element values.
- If total > mid, create a new subarray by resetting total to the current element and increment cnt.
- If cnt > k, return false (invalid condition).
- If the loop completes successfully, return true (valid condition).
- Implement Binary Search in splitArray()
- While low <= high:
- Calculate mid = (low + high) / 2.
- If isValid(nums, k, mid) is true, store mid as a potential answer and move high to mid - 1 to search for a smaller valid sum.
- Otherwise, move low to mid + 1 to increase the valid range.
- Return the Final Answer
- The stored answer will be the minimized maximum subarray sum.
Split Array Largest Sum Leetcode Solution
Split array largest sum Leetcode Solution / Code Implementation
1. Split array largest sum solution in C++ Try on Compiler
class Solution {
// Function to check if the given `mid` value is a valid maximum subarray sum
bool isValid(vector<int> &nums, int k, int mid)
{
// Initialize the count of subarrays and total sum
int cnt = 1;
int total = 0;
// Traverse each element in the array
for(auto &num : nums)
{
// Add current element to the total
total += num;
// If total exceeds `mid`, split the array
if(total > mid)
{
// Start a new subarray with the current element
total = num;
// Increment the subarray count
cnt++;
// If the number of subarrays exceeds `k`, return false
if(cnt > k)
return false;
}
}
// Return true if the condition is satisfied
return true;
}
public:
// Main function to find the minimized largest sum
int splitArray(vector<int>& nums, int k) {
// The minimum possible largest sum is the maximum element in the array
int low = *max_element(nums.begin(), nums.end());
// The maximum possible largest sum is the total sum of the array
int high = accumulate(nums.begin(), nums.end(), 0);
// Variable to store the final answer
int ans = 0;
// Binary search to find the optimal maximum subarray sum
while(low <= high)
{
// Calculate the middle value
int mid = (low + high) / 2;
// Check if this `mid` value is valid
if(isValid(nums, k, mid))
{
// Store the valid value as a potential answer
ans = mid;
// Try to find a smaller maximum sum
high = mid - 1;
}
else
{
// If `mid` is invalid, increase the lower bound
low = mid + 1;
}
}
// Return the minimized largest sum
return ans;
}
};
2. Split array largest sum solution in Java Try on Compiler
class Solution {
// Function to check if the given `mid` value is a valid maximum subarray sum
public boolean isValid(int[] nums, int k, int mid) {
// Initialize the count of subarrays and total sum
int cnt = 1;
int total = 0;
// Traverse each element in the array
for(int num : nums) {
// Add current element to the total
total += num;
// If total exceeds `mid`, split the array
if(total > mid) {
// Start a new subarray with the current element
total = num;
// Increment the subarray count
cnt++;
// If the number of subarrays exceeds `k`, return false
if(cnt > k)
return false;
}
}
// Return true if the condition is satisfied
return true;
}
// Main function to find the minimized largest sum
public int splitArray(int[] nums, int k) {
// The minimum possible largest sum is the maximum element in the array
int low = Arrays.stream(nums).max().getAsInt();
// The maximum possible largest sum is the total sum of the array
int high = Arrays.stream(nums).sum();
// Variable to store the final answer
int ans = 0;
// Binary search to find the optimal maximum subarray sum
while(low <= high) {
// Calculate the middle value
int mid = (low + high) / 2;
// Check if this `mid` value is valid
if(isValid(nums, k, mid)) {
// Store the valid value as a potential answer
ans = mid;
// Try to find a smaller maximum sum
high = mid - 1;
}
else {
// If `mid` is invalid, increase the lower bound
low = mid + 1;
}
}
// Return the minimized largest sum
return ans;
}
}
3. Split array largest sum solution in Python Try on Compiler
class Solution:
# Function to check if the given `mid` value is a valid maximum subarray sum
def isValid(self, nums, k, mid):
# Initialize the count of subarrays and total sum
cnt = 1
total = 0
# Traverse each element in the array
for num in nums:
# Add current element to the total
total += num
# If total exceeds `mid`, split the array
if total > mid:
# Start a new subarray with the current element
total = num
# Increment the subarray count
cnt += 1
# If the number of subarrays exceeds `k`, return False
if cnt > k:
return False
# Return True if the condition is satisfied
return True
# Main function to find the minimized largest sum
def splitArray(self, nums, k):
# The minimum possible largest sum is the maximum element in the array
low = max(nums)
# The maximum possible largest sum is the total sum of the array
high = sum(nums)
# Variable to store the final answer
ans = 0
# Binary search to find the optimal maximum subarray sum
while low <= high:
# Calculate the middle value
mid = (low + high) // 2
# Check if this `mid` value is valid
if self.isValid(nums, k, mid):
# Store the valid value as a potential answer
ans = mid
# Try to find a smaller maximum sum
high = mid - 1
else:
# If `mid` is invalid, increase the lower bound
low = mid + 1
# Return the minimized largest sum
return ans
4. Split array largest sum solution in Javascript Try on Compiler
/**
* @param {number[]} nums
* @param {number} k
* @return {number}
*/
// Function to check if the given `mid` value is a valid maximum subarray sum
function isValid(nums, k, mid) {
// Initialize the count of subarrays and total sum
let cnt = 1;
let total = 0;
// Traverse each element in the array
for(let num of nums) {
// Add current element to the total
total += num;
// If total exceeds `mid`, split the array
if(total > mid) {
// Start a new subarray with the current element
total = num;
// Increment the subarray count
cnt++;
// If the number of subarrays exceeds `k`, return false
if(cnt > k)
return false;
}
}
// Return true if the condition is satisfied
return true;
}
// Main function to find the minimized largest sum
var splitArray = function(nums, k) {
// The minimum possible largest sum is the maximum element in the array
let low = Math.max(...nums);
// The maximum possible largest sum is the total sum of the array
let high = nums.reduce((a, b) => a + b, 0);
// Variable to store the final answer
let ans = 0;
// Binary search to find the optimal maximum subarray sum
while(low <= high) {
// Calculate the middle value
let mid = Math.floor((low + high) / 2);
// Check if this `mid` value is valid
if(isValid(nums, k, mid)) {
// Store the valid value as a potential answer
ans = mid;
// Try to find a smaller maximum sum
high = mid - 1;
}
else {
// If `mid` is invalid, increase the lower bound
low = mid + 1;
}
}
// Return the minimized largest sum
return ans;
};
Split array largest sum Complexity Analysis (Binary Search)
Time Complexity: O(n × log(sum(nums) - max(nums)))
Time Complexity Analysis
Function isValid(nums, k, mid) Complexity:
- The isValid function iterates through the entire nums array to check if a given mid can split the array into k valid subarrays.
- Time Complexity of isValid: O(n)
Main Function splitArray(nums, k) Complexity:
- The binary search runs until the search space is reduced to zero.
- In each iteration, the binary search range reduces by half.
- The total number of binary search iterations is O(log(sum(nums) - max(nums))).
Total Time Complexity:
- For each binary search iteration, we run the isValid function, which takes O(n).
- The total number of iterations is O(log(sum(nums) - max(nums))).
Final Time Complexity: O(n × log(sum(nums) - max(nums)))
Space Complexity: O(n)
- Auxiliary Space Complexity: O(1)
The algorithm only uses a few integer variables like low, high, mid, ans, cnt, total, etc. These are just primitive variables that occupy O(1) space.
Therefore, the auxiliary space complexity is O(1). - Total Space Complexity: O(n)
The algorithm does not create any additional data structures apart from the given nums array.
The input array itself takes O(n) space, where n = size of nums.
Therefore, the total space complexity is O(n).
Can there be any other approach?
In this problem, we are given an array nums and a value k, where our goal is to split the array into k non-empty contiguous subarrays such that the maximum subarray sum is minimized.
At first glance, this seems simple — just split the array carefully.
However, the real challenge lies in efficiently determining where to split the array to achieve the minimum possible maximum subarray sum.
Consider the array nums = [7, 2, 5, 10, 8] with k = 2. If we split the array in different ways, we get various maximum subarray sums.
For example, splitting it as [7, 2, 5] | [10, 8] results in a maximum sum of 15, while splitting as [7] | [2, 5, 10, 8] gives a maximum sum of 25. Clearly, the way we partition the array drastically affects the outcome, and our task is to find the split that results in the smallest maximum sum.
To achieve this, we can break the problem down using recursion.
Suppose we are at index idx and have k partitions left. We can choose to end the first subarray at any position j starting from idx. This first subarray would include elements from nums[idx] to nums[j].
After forming this subarray, the remaining portion of the array must be divided into k - 1 partitions. Therefore, the answer for the current state would be the minimum of all possible combinations where we maximize the current subarray’s sum and the solution for the remaining array.
The idea is to recursively try every possible split point and track the best outcome. Imagine standing at the starting index of the array. From this point onward, you have two choices:
- Include the next element in the current subarray.
- Start a new subarray at the next index.
To implement this:
- Start at index 0.
- Try every possible split point (say at index j) and calculate the sum of the subarray from the current index to j.
- Recursively compute the result for the remaining elements with k - 1 splits remaining.
- Track the minimum of the maximum subarray sums among all possible partitions.
The recursive relation for this is:
solve(idx, k) = min(max(sum, solve(j + 1, k - 1)))
Here, sum represents the sum of the elements from index idx to j, and solve(j + 1, k - 1) is the recursive call for the remaining portion of the array. The logic here is intuitive — by iterating through all possible split points for the first partition, we can explore every possible way to divide the array.
The base condition is crucial in this recursion. If k == 0, meaning no partitions are left, we must return the sum of the remaining elements since there’s no further partitioning possible.
Additionally, if idx exceeds the array’s length, it signifies an invalid path, so we return infinity. With this approach, we effectively explore all possible ways to split the array, but this results in exponential complexity — O(2ⁿ) — since we are branching out at each step.
To optimize this, we introduce memorization.
Split Array Largest Sum Algorithm (Dynamic Programming)
Notice that in recursion, several states are revisited multiple times. For example, solve(3, 1) may be calculated repeatedly from different paths.
By storing the results of these states in a DP array, we can directly reuse the computed values instead of recalculating them.
The DP array is defined as dp[idx][k], where each entry represents the minimum maximum sum achievable starting from index idx with k partitions remaining.
We'll create a 2D DP array, where:
- dp[i][k] stores the minimum possible maximum subarray sum starting from index i with k splits remaining.
- If dp[i][k] has already been calculated, we return its stored value to avoid redundant calculations.
This combined approach ensures that we efficiently explore all possible splits without recomputing the same results, significantly improving the solution’s performance.
This optimization ensures that each unique state is computed only once, reducing the complexity to O(n² × k), which is significantly more efficient.
The key insight here is that recursion effectively models the problem by exploring possible splits, and memoization optimizes it by eliminating redundant calculations. By combining these two techniques, we achieve an optimal solution that efficiently determines the minimum possible maximum subarray sum.
Let's understand with an example:
Split Array Largest Sum Example:
Let's walk through a concise dry run of the recursion with memoization approach for the given input:
Input: nums = [1, 2, 3, 4, 5], k = 2
Step 1: Initial Call
Starting at index 0 with k = 1 (since we need k partitions, we'll make k - 1 splits).
solve(nums, 0, 1)
Step 2: Recursive Breakdown
We'll explore possible split points and calculate the subarray sums.
Split at index 0:
- Subarray: [1]
- Remaining call: solve(nums, 1, 0) → Remaining sum = 2 + 3 + 4 + 5 = 14
- Max sum so far: max(1, 14) = 14
Split at index 1:
- Subarray: [1, 2]
- Remaining call: solve(nums, 2, 0) → Remaining sum = 3 + 4 + 5 = 12
- Max sum so far: min(14, max(3, 12)) = 12
Split at index 2:
- Subarray: [1, 2, 3]
- Remaining call: solve(nums, 3, 0) → Remaining sum = 4 + 5 = 9
- Max sum so far: min(12, max(6, 9)) = 9
Split at index 3:
- Subarray: [1, 2, 3, 4]
- Remaining call: solve(nums, 4, 0) → Remaining sum = 5
- Max sum so far: min(9, max(10, 5)) = 9
Step 3: Memoization Table
- Store results in dp array to avoid redundant calls.
- Example: dp[0][1] = 9
Step 4: Final Answer
The minimum possible maximum subarray sum is 9, achieved by splitting the array as [1, 2, 3] and [4, 5].
How to code it up:
- Understand the Problem Statement:
- Given an array nums and an integer k, partition the array into k subarrays such that the maximum sum among these subarrays is minimized.
- Identify the Recursive Approach:
- Define a recursive function solve(nums, dp, idx, k) where:
- idx = Current index in the array.
- k = Remaining partitions to be made.
- Return the minimum possible maximum subarray sum starting from index idx with k partitions remaining.
- Write the Base Condition:
- If k == 0, compute the sum of all remaining elements and return it (since no more partitions are allowed).
- Memoization Step:
- If dp[idx][k] is already calculated (not -1), return its stored value to avoid redundant calculations.
- Recursive Logic for Exploring Partitions:
- Iterate from idx to the end of the array.
- Maintain a running sum of elements.
- For each partition point j, recursively compute the maximum subarray sum for the remaining elements.
- Track the minimum of these maximum values.
- Memoize the Result:
- Store the result in dp[idx][k] to ensure optimal subproblem reuse.
- Main Function (splitArray) Implementation:
- Initialize the DP table of size (n + 1) x (k + 1) with -1 (indicating uncomputed states).
- Start the recursion with idx = 0 and k - 1 (since one partition is already implied by starting the recursion).
- Return the Final Answer:
- The final answer is stored in dp[0][k - 1].
Split Array Largest Sum Leetcode Solution
Split array largest sum Leetcode Solution / Code Implementation
1. Split array largest sum solution in C++ Try on Compiler
class Solution {
public:
// Recursive function to find the minimum possible maximum subarray sum
long long solve(vector<int>& nums, vector<vector<int>> &dp, int idx, int k) {
// Base condition: If no more partitions are left
long long ans = INT_MAX;
long long sum = 0;
// When k == 0, calculate the sum of remaining elements in the array
if(k == 0) {
for(int j = idx; j < nums.size(); j++) {
sum += nums[j];
}
return sum;
}
// Return memoized value if already calculated
if(dp[idx][k] != -1) {
return dp[idx][k];
}
// Explore all possible partitions
for(int j = idx; j < nums.size(); j++) {
sum += nums[j]; // Add current element to sum
// Calculate the minimum of maximum sums by exploring further partitions
ans = min(ans, max(sum, solve(nums, dp, j + 1, k - 1)));
}
// Memoize the result for future reference
return dp[idx][k] = ans;
}
// Main function to split the array into k parts with minimized largest sum
int splitArray(vector<int>& nums, int k) {
// Initialize DP table with -1 (indicating uncalculated states)
vector<vector<int>> dp(nums.size() + 1, vector<int>(k + 1, -1));
// Call the recursive function starting from index 0 with k - 1 splits remaining
return solve(nums, dp, 0, k - 1);
}
};
2. Split array largest sum solution in Java Try on Compiler
class Solution {
// Recursive function to find the minimum possible maximum subarray sum
public long solve(int[] nums, long[][] dp, int idx, int k) {
// Base condition: If no more partitions are left
long ans = Long.MAX_VALUE;
long sum = 0;
// When k == 0, calculate the sum of remaining elements in the array
if (k == 0) {
for (int j = idx; j < nums.length; j++) {
sum += nums[j];
}
return sum;
}
// Return memoized value if already calculated
if (dp[idx][k] != -1) {
return dp[idx][k];
}
// Explore all possible partitions
for (int j = idx; j < nums.length; j++) {
sum += nums[j]; // Add current element to sum
// Calculate the minimum of maximum sums by exploring further partitions
ans = Math.min(ans, Math.max(sum, solve(nums, dp, j + 1, k - 1)));
}
// Memoize the result for future reference
return dp[idx][k] = ans;
}
// Main function to split the array into k parts with minimized largest sum
public int splitArray(int[] nums, int k) {
// Initialize DP table with -1 (indicating uncalculated states)
long[][] dp = new long[nums.length + 1][k + 1];
for (int i = 0; i <= nums.length; i++) {
for (int j = 0; j <= k; j++) {
dp[i][j] = -1;
}
}
// Call the recursive function starting from index 0 with k - 1 splits remaining
return (int) solve(nums, dp, 0, k - 1);
}
}
3. Split array largest sum solution in Python Try on Compiler
class Solution:
# Recursive function to find the minimum possible maximum subarray sum
def solve(self, nums, dp, idx, k):
# Base condition: If no more partitions are left
ans = float('inf')
total_sum = 0
# When k == 0, calculate the sum of remaining elements in the array
if k == 0:
for j in range(idx, len(nums)):
total_sum += nums[j]
return total_sum
# Return memoized value if already calculated
if dp[idx][k] != -1:
return dp[idx][k]
# Explore all possible partitions
for j in range(idx, len(nums)):
total_sum += nums[j] # Add current element to total_sum
# Calculate the minimum of maximum sums by exploring further partitions
ans = min(ans, max(total_sum, self.solve(nums, dp, j + 1, k - 1)))
# Memoize the result for future reference
dp[idx][k] = ans
return ans
# Main function to split the array into k parts with minimized largest sum
def splitArray(self, nums, k):
# Initialize DP table with -1 (indicating uncalculated states)
dp = [[-1] * (k + 1) for _ in range(len(nums) + 1)]
# Call the recursive function starting from index 0 with k - 1 splits remaining
return self.solve(nums, dp, 0, k - 1)
4. Split array largest sum solution in Javascript Try on Compiler
/**
* @param {number[]} nums
* @param {number} k
* @return {number}
*/
var splitArray = function(nums, k) {
// Recursive function to find the minimum possible maximum subarray sum
var solve = function(nums, dp, idx, k) {
// Initialize answer with infinity
var ans = Infinity;
var sum = 0;
// Base condition: If no more partitions are left
if (k === 0) {
// Calculate the sum of remaining elements in the array
for (var j = idx; j < nums.length; j++) {
sum += nums[j];
}
return sum;
}
// Return memoized value if already calculated
if (dp[idx][k] !== -1) {
return dp[idx][k];
}
// Explore all possible partitions
for (var j = idx; j < nums.length; j++) {
sum += nums[j]; // Add current element to sum
// Calculate the minimum of maximum sums by exploring further partitions
ans = Math.min(ans, Math.max(sum, solve(nums, dp, j + 1, k - 1)));
}
// Memoize the result for future reference
dp[idx][k] = ans;
return ans;
};
// Initialize DP table with -1 (indicating uncalculated states)
var dp = Array.from({ length: nums.length + 1 }, () => Array(k + 1).fill(-1));
// Call the recursive function starting from index 0 with k - 1 splits remaining
return solve(nums, dp, 0, k - 1);
};
Split array largest sum Complexity Analysis (Dynamic Programming)
Time Complexity: O(n² × k)
The given solution uses recursion with memoization (top-down dynamic programming) to solve the problem. Let's analyze its time complexity step by step.
Step 1: Understanding the Recursive Tree Structure
- The recursive function solve(nums, dp, idx, k) is called at most n × k times where:
- n = Length of the nums array
- k = Number of partitions (subarrays)
- For each recursive call at index idx, the loop iterates from idx to nums.length.
- In the worst case, this loop can iterate O(n) times.
Step 2: Maximum Number of Recursive Calls
- Each state (idx, k) is stored in the DP table.
- The DP table is of size (n + 1) × (k + 1), meaning there are O(n × k) unique states.
- Each state is visited once because of memoization, ensuring we never compute the same state twice.
Step 3: Total Complexity
- Since each state can take O(n) iterations in its internal loop, the overall complexity becomes: O(n × k × n) = O(n² × k)
Space Complexity: O(n × k)
- Auxiliary Space Complexity: O(n × k)
The algorithm utilizes a DP table of size (n + 1) × (k + 1). This table stores results for previously calculated states to avoid redundant calculations. Since this is the only additional data structure apart from a few integer variables like ans, sum, etc., the auxiliary space complexity is O(n × k). - Total Space Complexity: O(n × k)
In addition to the input array, the DP table occupies O(n × k) space. Since the input array itself takes O(n) space, the total space complexity is dominated by the DP table, making it O(n × k).
Similar Problems
The Split Array Largest Sum problem is a classic array partitioning challenge that can be solved using different approaches like Binary Search, Dynamic Programming, Greedy, and Prefix Sum. A Greedy approach can help in checking whether a given partitioning is possible, while Binary Search on Answer efficiently finds the minimum possible largest sum by narrowing down the search space. Dynamic Programming provides an alternative way by breaking the problem into subproblems and computing optimal partitions step by step. Meanwhile, Prefix Sum is useful for quickly computing subarray sums, reducing redundant calculations. By combining these techniques, we can efficiently solve the problem while balancing time complexity and implementation ease.
Now that we have successfully tackled this problem, let's try similar problems.
A conveyor belt has packages that must be shipped from one port to another within D days.The ith package on the conveyor belt has a weight of weights[i]. Each day, we load the ship with packages on the conveyor belt (in the order given by weights). We may not load more weight than the maximum weight capacity of the ship.Return the least weight capacity of the ship that will result in all the packages on the conveyor belt being shipped within D days.
2. Sqrt(x)
Given a non-negative integer x, return the square root of x rounded down to the nearest integer. The returned integer should be non-negative as well.You must not use any built-in exponent function or operator.For example, do not use pow(x, 0.5) in C++ or x ** 0.5 in Python.
You have one chocolate bar that consists of some chunks. Each chunk has its own sweetness given by the array sweetness.
You want to share the chocolate with your K friends so you start cutting the chocolate bar into K+1 pieces using K cuts, each piece consists of some consecutive chunks.
Being generous, you will eat the piece with the minimum total sweetness and give the other pieces to your friends.
Find the maximum total sweetness of the piece you can get by cutting the chocolate bar optimally.
You are given an integer array cookies, where cookies[i] denotes the number of cookies in the ith bag. You are also given an integer k that denotes the number of children to distribute all the bags of cookies to. All the cookies in the same bag must go to the same child and cannot be split up.
The unfairness of a distribution is defined as the maximum total cookies obtained by a single child in the distribution.
Return the minimum unfairness of all distributions.
You are given an integer array nums and an integer k. Find the largest even sum of any subsequence of nums that has a length of k.
Return this sum, or -1 if such a sum does not exist.
A subsequence is an array that can be derived from another array by deleting some or no elements without changing the order of the remaining elements.
Alice is a caretaker of n gardens and she wants to plant flowers to maximize the total beauty of all her gardens.
You are given a 0-indexed integer array flowers of size n, where flowers[i] is the number of flowers already planted in the ith garden. Flowers that are already planted cannot be removed. You are then given another integer newFlowers, which is the maximum number of flowers that Alice can additionally plant. You are also given the integers target, full, and partial.
A garden is considered complete if it has at least target flowers. The total beauty of the gardens is then determined as the sum of the following:
The number of complete gardens multiplied by full.
The minimum number of flowers in any of the incomplete gardens multiplied by partial. If there are no incomplete gardens, then this value will be 0.
Return the maximum total beauty that Alice can obtain after planting at most newFlowers flowers.
You are given a 0-indexed integer array nums of length n.
nums contains a valid split at index i if the following are true:
The sum of the first i + 1 elements is greater than or equal to the sum of the last n - i - 1 elements.
There is at least one element to the right of i. That is, 0 <= i < n - 1.
Return the number of valid splits in nums.
You are given an integer array nums and an integer k.
Split the array into some number of non-empty subarrays. The cost of a split is the sum of the importance value of each subarray in the split.
Let trimmed(subarray) be the version of the subarray where all numbers which appear only once are removed.
For example, trimmed([3,1,2,4,3,4]) = [3,4,3,4].
The importance value of a subarray is k + trimmed(subarray).length.
For example, if a subarray is [1,2,3,3,3,4,4], then trimmed([1,2,3,3,3,4,4]) = [3,3,3,4,4].The importance value of this subarray will be k + 5.
Return the minimum possible cost of a split of nums.
A subarray is a contiguous non-empty sequence of elements within an array.
You are given a 1-indexed array of distinct integers nums of length n.
You need to distribute all the elements of nums between two arrays arr1 and arr2 using n operations. In the first operation, append nums[1] to arr1. In the second operation, append nums[2] to arr2. Afterwards, in the ith operation:
- If the last element of
arr1is greater than the last element ofarr2, appendnums[i]toarr1. Otherwise, appendnums[i]toarr2.
The array result is formed by concatenating the arrays arr1 and arr2. For example, if arr1 == [1,2,3] and arr2 == [4,5,6], then result = [1,2,3,4,5,6].
Return the array result.
You are given a 1-indexed array of integers nums of length n.
We define a function greaterCount such that greaterCount(arr, val) returns the number of elements in arr that are strictly greater than val.
You need to distribute all the elements of nums between two arrays arr1 and arr2 using n operations. In the first operation, append nums[1] to arr1. In the second operation, append nums[2] to arr2. Afterwards, in the ith operation:
- If
greaterCount(arr1, nums[i]) > greaterCount(arr2, nums[i]), appendnums[i]toarr1. - If
greaterCount(arr1, nums[i]) < greaterCount(arr2, nums[i]), appendnums[i]toarr2. - If
greaterCount(arr1, nums[i]) == greaterCount(arr2, nums[i]), appendnums[i]to the array with a lesser number of elements. - If there is still a tie, append
nums[i]toarr1.
The array result is formed by concatenating the arrays arr1 and arr2. For example, if arr1 == [1,2,3] and arr2 == [4,5,6], then result = [1,2,3,4,5,6].
Return the integer array result.