Search a 2D Matrix II Solution In C++/Java/Python/JS
Problem Description
Write an efficient algorithm that searches for a value target in an m x n integer matrix matrix. This matrix has the following properties:
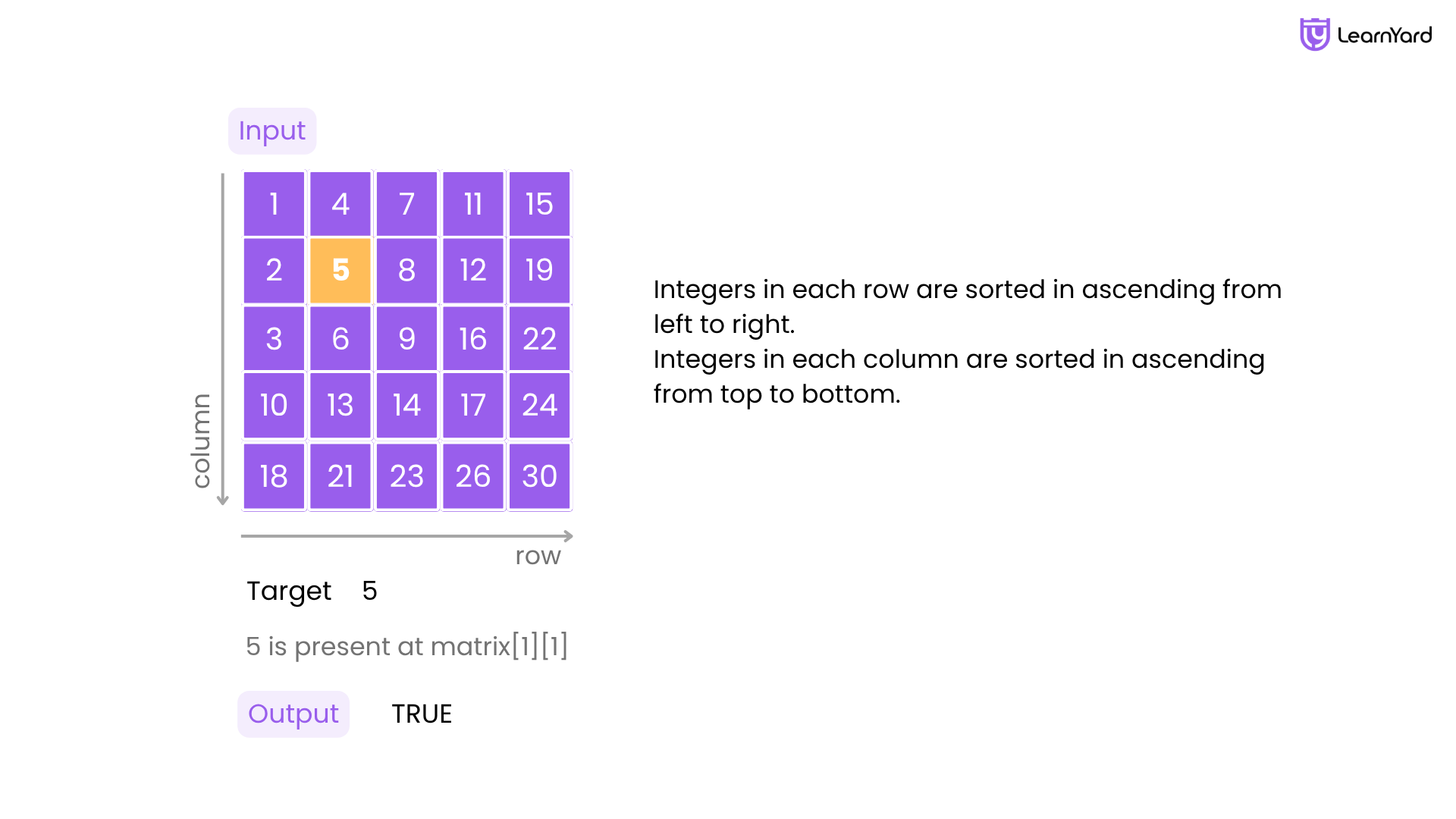
Integers in each row are sorted in ascending from left to right.
Integers in each column are sorted in ascending from top to bottom.
How's this problem different from Search a 2D Matrix
In the first problem, Search a 2D Matrix, the entire matrix behaves almost like one long sorted list: each row is sorted left to right, and also, importantly, the first number of each row is bigger than the last number of the previous row.
Whereas in the second problem, Search a 2D Matrix II, each row is still sorted left to right, and each column is sorted top to bottom—but there’s no rule connecting the last number of one row to the first number of the next row. This means you can’t flatten it into one list
Examples
Input: matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 5
Output: true
Input: matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 20
Output: false
Constraints
m == matrix.length
n == matrix[i].length
1 <= n, m <= 300
-109 <= matrix[i][j] <= 109
All the integers in each row are sorted in ascending order.
All the integers in each column are sorted in ascending order.
-109 <= target <= 109
In this problem, we need to search for a target number in a 2D matrix where each row and each column is sorted in ascending order.
Before thinking of an optimized solution, let’s start with a simple brute force approach: check every element one by one to see if it matches the target.
Brute Force Approach
Intuition:
The problem asks us to find whether a given target exists in a matrix where:
– Each row is sorted in ascending order from left to right, and
– Each column is sorted in ascending order from top to bottom.
The simplest idea that comes to mind is to check every element one by one to see if it matches the target.
How do we do this?
We can use two nested loops:
– The outer loop iterates over each row of the matrix (from index 0 to m – 1).
– The inner loop iterates over each element in the current row (from index 0 to n – 1).
At each cell matrix[i][j], we check:
– If matrix[i][j] == target, we can directly return true.
– If no cell matches the target after checking all elements, we return false.
Although the matrix is sorted both row-wise and column-wise, this brute-force method doesn’t use that information; it simply scans every cell directly to find the target.
Approach
Step 1: Initialize the answer variable
Create a Boolean variable found to indicate whether the target is present in the matrix.
Set found = false initially.
Step 2: Loop over each row of the matrix
Use an outer loop where i ranges from 0 to m - 1 (where m is the number of rows).
This loop picks every row of the matrix one by one.
Step 3: Loop over each element of the current row
For each row i, use another loop where j ranges from 0 to n - 1 (where n is the number of columns).
This loop checks every element in that row.
Step 4: Check if the current element equals the target
For each cell matrix[i][j], check:
If matrix[i][j] == target, it means we found the target.
Step 5: Set found to true if target is found
If the condition is true, we can set found to true since we found the target and break.
Step 6: After all loops, return the Boolean found
Finally return found that indicates whether target exists in the matrix or not
Dry Run
Here’s the detailed dry run of the brute-force approach using nested loops for Input: matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 5
Step 1: Understand the matrix
Original matrix:
Row 0 → 1,4,7,11,151, 4, 7, 11, 151,4,7,11,15
Row 1 → 2,5,8,12,192, 5, 8, 12, 192,5,8,12,19
Row 2 → 3,6,9,16,223, 6, 9, 16, 223,6,9,16,22
Row 3 → 10,13,14,17,2410, 13, 14, 17, 2410,13,14,17,24
Row 4 → 18,21,23,26,3018, 21, 23, 26, 3018,21,23,26,30
Number of rows (m) = 5
Number of columns (n) = 5
Initialize found = false → this will store whether we found the target.
Step 2: Use nested loops to check every element
We will:
– Loop over each row index i from 0 to 4
– Inside each row, loop over each column index j from 0 to 4
– For each cell matrix[i][j], check if it equals target.
Iteration-Wise Dry Run
i = 0 (first row: 1,4,7,11,151, 4, 7, 11, 151,4,7,11,15)
• j=0: matrix000000=1 → not equal to 5 → found remains false
• j=1: matrix000111=4 → not equal to 5 → found remains false
• j=2: matrix000222=7 → not equal to 5 → found remains false
• j=3: matrix000333=11 → not equal to 5 → found remains false
• j=4: matrix000444=15 → not equal to 5 → found remains false
i = 1 (second row: 2,5,8,12,192, 5, 8, 12, 192,5,8,12,19)
• j=0: matrix111000=2 → not equal to 5 → found remains false
• j=1: matrix111111=5 → equal to 5 → set found = true → break inner loop
Since we found the target, we can immediately stop checking further rows.
Final Result
Target = 5 is found → return true.
Code for All Languages
C++
#include <iostream> // For input and output
#include <vector> // For using vector
using namespace std;
class Solution {
public:
bool searchMatrix(vector<vector<int>>& matrix, int target) {
int m = matrix.size(); // Number of rows
int n = matrix[0].size(); // Number of columns
bool found = false; // Step 1: Initialize the answer variable
// Step 2: Loop over each row of the matrix
for (int i = 0; i < m; i++) {
// Step 3: Loop over each element of the current row
for (int j = 0; j < n; j++) {
// Step 4: Check if the current element equals the target
if (matrix[i][j] == target) {
// Step 5: Set found to true if target is found
found = true;
break; // Since we found the target, no need to continue in this row
}
}
// If found, no need to check remaining rows
if (found) {
break;
}
}
// Step 6: After all loops, return the Boolean found
return found;
}
};
int main() {
int m, n, target;
cin >> m >> n >> target; // Input number of rows, columns, and target
vector<vector<int>> matrix(m, vector<int>(n));
// Input the matrix elements
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
cin >> matrix[i][j];
}
}
Solution sol;
bool result = sol.searchMatrix(matrix, target);
// Output the result
if (result) {
cout << "true" << endl;
} else {
cout << "false" << endl;
}
return 0;
}
Java
import java.util.*; // For Scanner
class Solution {
public boolean searchMatrix(int[][] matrix, int target) {
int m = matrix.length; // Number of rows
int n = matrix[0].length; // Number of columns
boolean found = false; // Step 1: Initialize the answer variable
// Step 2: Loop over each row of the matrix
for (int i = 0; i < m; i++) {
// Step 3: Loop over each element of the current row
for (int j = 0; j < n; j++) {
// Step 4: Check if the current element equals the target
if (matrix[i][j] == target) {
// Step 5: Set found to true if target is found
found = true;
break; // Since we found the target, break out of inner loop
}
}
// If found, break out of outer loop too
if (found) {
break;
}
}
// Step 6: After all loops, return the Boolean found
return found;
}
}
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
// Input number of rows, columns, and target
int m = sc.nextInt();
int n = sc.nextInt();
int target = sc.nextInt();
int[][] matrix = new int[m][n];
// Input the matrix elements
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
matrix[i][j] = sc.nextInt();
}
}
Solution sol = new Solution();
boolean result = sol.searchMatrix(matrix, target);
// Output the result
System.out.println(result ? "true" : "false");
}
}
Python
from typing import List # For specifying the return type
class Solution:
def searchMatrix(self, matrix: List[List[int]], target: int) -> bool:
# Step 1: Initialize the answer variable
found = False # Create a variable found to indicate whether the target is present in the matrix
# Step 2: Loop over each row of the matrix
for i in range(len(matrix)):
row = matrix[i]
# Step 3: Loop over each element of the current row
for j in range(len(row)):
cell = row[j]
# Step 4: Check if the current element equals the target
if cell == target:
# Step 5: Set found to true if target is found
found = True
break # Break since we found the target
if found:
break # Break outer loop too if target is already found
# Step 6: Return found as the required value
return found # Final answer representing whether the target exists in the matrix
# Driver Code
if __name__ == "__main__":
m = int(input()) # Input the number of rows
n = int(input()) # Input the number of columns
target = int(input()) # Input the target value
matrix = []
for _ in range(m):
row = list(map(int, input().split())) # Input each row as space-separated integers
matrix.append(row)
sol = Solution()
ans = sol.searchMatrix(matrix, target)
print("true" if ans else "false") # Output whether the target exists in the matrix
Javascript
/**
* @param {number[][]} matrix - 2D array representing the matrix of numbers
* @param {number} target - The target number to search for
* @return {boolean} - Whether the target exists in the matrix
*/
var searchMatrix = function(matrix, target) {
// Step 1: Initialize the answer variable
let found = false; // Create a variable found to indicate whether the target is present in the matrix
// Step 2: Loop over each row of the matrix
for (let i = 0; i < matrix.length; i++) {
let row = matrix[i];
// Step 3: Loop over each element of the current row
for (let j = 0; j < row.length; j++) {
let cell = row[j];
// Step 4: Check if the current element equals the target
if (cell === target) {
// Step 5: Set found to true if target is found
found = true;
break; // Break since we found the target
}
}
if (found) {
break; // Break outer loop too if target is already found
}
}
// Step 6: Return found as the required value
return found; // Final answer representing whether the target exists in the matrix
};
// Driver code
const readline = require("readline");
const rl = readline.createInterface({
input: process.stdin,
output: process.stdout
});
let inputs = [];
let m = 0, n = 0, target = 0, rowCount = 0;
rl.on("line", function(line) {
if (inputs.length === 0) {
m = parseInt(line.trim()); // Input the number of rows
inputs.push(m);
} else if (inputs.length === 1) {
n = parseInt(line.trim()); // Input the number of columns
inputs.push(n);
} else if (inputs.length === 2) {
target = parseInt(line.trim()); // Input the target number
inputs.push(target);
} else {
let row = line.trim().split(' ').map(Number); // Input each row as space-separated integers
inputs.push(row);
rowCount++;
if (rowCount === m) {
let matrix = inputs.slice(3); // Extract the matrix part
let ans = searchMatrix(matrix, target);
console.log(ans ? "true" : "false"); // Output whether the target exists in the matrix
rl.close();
}
}
});
Time Complexity: O(m × n)
Let us denote:
m = number of rows in the matrix
n = number of columns in the matrix
Initialization:
– The variable found is initialized to false before starting the loops.
– Time complexity: O(1) (constant time).
Outer Loop Over Rows:
– The outer loop iterates over all m rows in the matrix.
– Time complexity for this loop: O(m).
Inner Loop Over Columns:
– For each row, the inner loop iterates over all n columns (elements in that row).
– Time complexity for each row: O(n).
Checking Each Element:
– Inside the inner loop, we check whether matrix[i][j] == target.
– Time complexity for each check: O(1).
Total:
– For each of the m rows, we do n operations.
– Therefore, the total time complexity becomes:
O(m) × O(n) = O(m × n).
Space Complexity: O(m × n)
Let us denote:
m = number of rows in the matrix
n = number of columns in the matrix
Auxiliary Space Complexity:
– Definition: The extra space or temporary space used by the algorithm during its execution, excluding the input data.
– Code Analysis: The algorithm uses only a few variables:
– found to indicate whether the target is present in the matrix.
– Loop variables i, j, and possibly a temporary variable for each cell checked.
– All these variables require constant space regardless of the size of the input.
– Therefore, Auxiliary Space Complexity = O(1).
Total Space Complexity:
– The overall space used by the algorithm includes the input data and the auxiliary space.
– Input Data: The input matrix itself is a 2D array with m rows and n columns, which requires O(m × n) space.
– Auxiliary Space: As analyzed above, this is O(1).
– Combining:
– Total space complexity = O(m × n) + O(1) = O(m × n).
Is the brute force approach efficient?
Given the problem constraints where the matrix dimensions satisfy 1 ≤ m, n ≤ 300, the brute force approach is actually quite practical.
Even though the method checks each cell individually with time complexity O(m × n), the total number of operations becomes at most 300 × 300 = 90,000, which modern computers handle almost instantly.
Since m and n are relatively small, we don’t need to optimize further, and directly looping through every element is clear, easy to implement, and guaranteed to run within time limits.
Therefore, despite sounding inefficient in theory, the brute force solution is perfectly acceptable for this problem’s constraints and works reliably in practice.
We have seen the brute-force solution, which checks each element one by one to find the target. Although correct, it takes O(m × n) time. But since the matrix rows are sorted and each first element is greater than the last of the previous row, can we use these properties to search faster? Let’s see this in the better approach.
Better Approach
Intuition
We are given a grid where each row is sorted in non-decreasing order, and the first integer of each row is greater than the last integer of the previous row.
Let’s first understand what this means. A sorted row means the elements increase as we move left to right.
For example: [10, 11, 16, 20]
In this row:
– All elements are sorted in increasing order.
Because the first element of each row is greater than the last element of the previous row, the entire matrix behaves like one big sorted list from top-left to bottom-right.
Divide the matrix into logical parts
Observation: Since the first element of a row is greater than the last element of the previous row, the target must fall between matrix[i][0] and matrix[i][n - 1] if it exists in row i.
Key Observations
Finding the correct row:
Observation: We don’t need to search every row. We can first check if
target ≥ matrix[i][0] and target ≤ matrix[i][n - 1].
Explanation: If the target falls outside this range, it can’t be in that row because all elements before or after are strictly smaller or larger.
Binary Search inside the row:
Pick any index mid in the row. It will either:
– Match the target
– Be smaller than the target
– Be greater than the target
Case 1: mid element equals target
Example: matrix[i][mid] == target
Conclusion: We immediately return true, since we found the target.
Case 2: mid element is smaller than target
Example: matrix[i][mid] < target
Conclusion: Since the row is sorted in increasing order, the target must be to the right of mid.
We move binary search to the right half: mid + 1 to end.
Case 3: mid element is greater than target
Example: matrix[i][mid] > target
Conclusion: Since the row is sorted, the target must be to the left of mid.
We move binary search to the left half: start to mid - 1.
The key idea:
– Use the matrix structure to narrow down the possible rows.
– Apply binary search within each valid row to check if the target exists.
This avoids checking every cell and also avoids actually flattening the entire matrix.
So, this approach is efficient, clean, and uses the matrix’s properties smartly to search quickly. Isn’t it intuitive?
Approach
Step 1: Initialize the answer variable
Create a Boolean variable found to indicate whether the target is present in the matrix.
Initially set found = false.
Step 2: Loop over each row of the matrix
Use an outer loop i that ranges from 0 to m - 1 (where m is the number of rows).
Step 3: Check if the target could be in the current row
For row i, check if
target ≥ matrix[i][0] and target ≤ matrix[i][n - 1] (where n is the number of columns).
If not, skip to the next row.
Step 4: Apply binary search in the current row
If the target could be in this row, initialize two pointers: start = 0 and end = n - 1.
While start ≤ end, do the following:
Step 5: Compute the middle index
Compute mid = floor((start + end) / 2).
Step 6: Case 1 – If matrix[i][mid] == target
Observation: We found the target in this row.
Conclusion: Set found = true and break out of the loop.
Step 7: Case 2 – If matrix[i][mid] < target
Observation: mid element is smaller than target.
Conclusion: The target must be to the right of mid.
So, move start = mid + 1.
Step 8: Case 3 – If matrix[i][mid] > target
Observation: mid element is greater than target.
Conclusion: The target must be to the left of mid.
So, move end = mid - 1.
Step 9: After binary search, check if found is true
If found, return true immediately because the target exists in the matrix.
Step 10: After checking all rows, return the final answer
If we finish all rows and found is still false, return false to indicate the target does not exist in the matrix.
Let us understand this with a video,
Dry Run
Here’s the detailed dry run of the binary search approach for the input:
matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 5
Number of rows (m) = 5
Number of columns (n) = 5
We need to check each row to see if it could contain the target, then apply binary search.
Initialize found = false → this will indicate whether the target is present.
Row-wise Dry Run
Row 0: [1, 4, 7, 11, 15]
Check if target could be in this row:
target = 5, matrix[0][0] = 1, matrix[0][4] = 15
5 ≥ 1 and 5 ≤ 15 → target could be here.
start = 0, end = 4
Iteration 1:
mid = floor((0+4)/2) = 2
matrix[0][2] = 7 > target
→ mid element is greater than target.
Move end = mid - 1 → end = 1
Iteration 2:
start = 0, end = 1
mid = floor((0+1)/2) = 0
matrix[0][0] = 1 < target
→ mid element is smaller than target.
Move start = mid + 1 → start = 1
Iteration 3:
start = 1, end = 1
mid = 1
matrix[0][1] = 4 < target
→ mid element is smaller than target.
Move start = mid + 1 → start = 2
Now start = 2, end = 1 → loop ends.
Did we find the target? No, found remains false.
Row 1: [2, 5, 8, 12, 19]
Check if target could be in this row:
target = 5, matrix[1][0] = 2, matrix[1][4] = 19
5 ≥ 2 and 5 ≤ 19 → target could be here.
start = 0, end = 4
Iteration 1:
mid = floor((0+4)/2) = 2
matrix[1][2] = 8 > target
→ mid element is greater than target.
Move end = mid - 1 → end = 1
Iteration 2:
start = 0, end = 1
mid = floor((0+1)/2) = 0
matrix[1][0] = 2 < target
→ mid element is smaller than target.
Move start = mid + 1 → start = 1
Iteration 3:
start = 1, end = 1
mid = 1
matrix[1][1] = 5 == target
→ Found the target
Set found = true and break.
Since we found the target, we stop checking further rows.
Final Result
After checking, found = true → return true.
Code for All Languages
C++
#include <iostream> // For input and output
#include <vector> // For using vector
using namespace std;
class Solution {
public:
bool searchMatrix(vector<vector<int>>& matrix, int target) {
int m = matrix.size(); // Number of rows
int n = matrix[0].size(); // Number of columns
bool found = false; // Step 1: Initialize the answer variable
// Create a Boolean variable found to indicate whether the target is present in the matrix.
// Initially set found = false.
// Step 2: Loop over each row of the matrix
// Use an outer loop i that ranges from 0 to m - 1 (where m is the number of rows).
for (int i = 0; i < m; i++) {
// Step 3: Check if the target could be in the current row
// For row i, check if target ≥ matrix[i][0] and target ≤ matrix[i][n - 1].
if (target >= matrix[i][0] && target <= matrix[i][n - 1]) {
// Step 4: Apply binary search in the current row
// If the target could be in this row, initialize two pointers: start = 0 and end = n - 1.
int start = 0, end = n - 1;
// While start ≤ end, do the following:
while (start <= end) {
// Step 5: Compute the middle index
// Compute mid = floor((start + end) / 2).
int mid = (start + end) / 2;
// Step 6: Case 1 – If matrix[i][mid] == target
// Observation: We found the target in this row.
// Conclusion: Set found = true and break out of the loop.
if (matrix[i][mid] == target) {
found = true;
break;
}
// Step 7: Case 2 – If matrix[i][mid] < target
// Observation: mid element is smaller than target.
// Conclusion: The target must be to the right of mid.
// So, move start = mid + 1.
else if (matrix[i][mid] < target) {
start = mid + 1;
}
// Step 8: Case 3 – If matrix[i][mid] > target
// Observation: mid element is greater than target.
// Conclusion: The target must be to the left of mid.
// So, move end = mid - 1.
else {
end = mid - 1;
}
}
}
// Step 9: After binary search, check if found is true
// If found, return true immediately because the target exists in the matrix.
if (found) {
return true;
}
}
// Step 10: After checking all rows, return the final answer
// If we finish all rows and found is still false, return false to indicate the target does not exist in the matrix.
return false;
}
};
int main() {
int m, n, target;
cin >> m >> n >> target; // Input number of rows, columns, and target
vector<vector<int>> matrix(m, vector<int>(n));
// Input the matrix elements
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
cin >> matrix[i][j];
}
}
Solution sol;
bool result = sol.searchMatrix(matrix, target);
// Output the result
if (result) {
cout << "true" << endl;
} else {
cout << "false" << endl;
}
return 0;
}
Java
import java.util.*; // For Scanner
class Solution {
public boolean searchMatrix(int[][] matrix, int target) {
int m = matrix.length; // Number of rows
int n = matrix[0].length; // Number of columns
boolean found = false; // Step 1: Initialize the answer variable
// Create a Boolean variable found to indicate whether the target is present in the matrix.
// Initially set found = false.
// Step 2: Loop over each row of the matrix
// Use an outer loop i that ranges from 0 to m - 1 (where m is the number of rows).
for (int i = 0; i < m; i++) {
// Step 3: Check if the target could be in the current row
// For row i, check if target ≥ matrix[i][0] and target ≤ matrix[i][n - 1].
if (target >= matrix[i][0] && target <= matrix[i][n - 1]) {
// Step 4: Apply binary search in the current row
// Initialize two pointers: start = 0 and end = n - 1.
int start = 0, end = n - 1;
// While start ≤ end, do the following:
while (start <= end) {
// Step 5: Compute the middle index
int mid = (start + end) / 2;
// Step 6: Case 1 – If matrix[i][mid] == target
if (matrix[i][mid] == target) {
found = true;
break; // We found the target, exit binary search
}
// Step 7: Case 2 – If matrix[i][mid] < target
else if (matrix[i][mid] < target) {
start = mid + 1;
}
// Step 8: Case 3 – If matrix[i][mid] > target
else {
end = mid - 1;
}
}
}
// Step 9: After binary search, check if found is true
if (found) {
return true; // Return true immediately if target is found
}
}
// Step 10: After checking all rows, return the final answer
return false; // Target does not exist in the matrix
}
}
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
// Input number of rows, columns, and target
int m = sc.nextInt();
int n = sc.nextInt();
int target = sc.nextInt();
int[][] matrix = new int[m][n];
// Input the matrix elements
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
matrix[i][j] = sc.nextInt();
}
}
Solution sol = new Solution();
boolean result = sol.searchMatrix(matrix, target);
// Output the result
System.out.println(result ? "true" : "false");
}
}
Python
from typing import List # For specifying the return type
class Solution:
def searchMatrix(self, matrix: List[List[int]], target: int) -> bool:
# Step 1: Initialize the answer variable
found = False # Create a variable found to indicate whether the target is present in the matrix
# Initially set found = False
# Step 2: Loop over each row of the matrix
for i in range(len(matrix)):
# Step 3: Check if the target could be in the current row
if target >= matrix[i][0] and target <= matrix[i][-1]:
# Step 4: Apply binary search in the current row
start = 0
end = len(matrix[i]) - 1
while start <= end:
# Step 5: Compute the middle index
mid = (start + end) // 2
# Step 6: Case 1 – If matrix[i][mid] == target
if matrix[i][mid] == target:
found = True
break # We found the target, exit binary search
# Step 7: Case 2 – If matrix[i][mid] < target
elif matrix[i][mid] < target:
start = mid + 1
# Step 8: Case 3 – If matrix[i][mid] > target
else:
end = mid - 1
# Step 9: After binary search, check if found is true
if found:
return True # Return immediately if target is found
# Step 10: After checking all rows, return the final answer
return False # Target does not exist in the matrix
# Driver Code
if __name__ == "__main__":
m = int(input()) # Input the number of rows
n = int(input()) # Input the number of columns
target = int(input()) # Input the target value
matrix = []
for _ in range(m):
row = list(map(int, input().split())) # Input each row as space-separated integers
matrix.append(row)
sol = Solution()
ans = sol.searchMatrix(matrix, target)
print("true" if ans else "false") # Output whether the target exists in the matrix
Javascript
/**
* @param {number[][]} matrix - 2D array representing the matrix of numbers
* @param {number} target - The target number to search for
* @return {boolean} - Whether the target exists in the matrix
*/
var searchMatrix = function(matrix, target) {
// Step 1: Initialize the answer variable
let found = false; // Create a variable found to indicate whether the target is present in the matrix
// Initially set found = false
// Step 2: Loop over each row of the matrix
for (let i = 0; i < matrix.length; i++) {
// Step 3: Check if the target could be in the current row
if (target >= matrix[i][0] && target <= matrix[i][matrix[i].length - 1]) {
// Step 4: Apply binary search in the current row
let start = 0;
let end = matrix[i].length - 1;
while (start <= end) {
// Step 5: Compute the middle index
let mid = Math.floor((start + end) / 2);
// Step 6: Case 1 – If matrix[i][mid] == target
if (matrix[i][mid] === target) {
found = true;
break; // Break since we found the target
}
// Step 7: Case 2 – If matrix[i][mid] < target
else if (matrix[i][mid] < target) {
start = mid + 1;
}
// Step 8: Case 3 – If matrix[i][mid] > target
else {
end = mid - 1;
}
}
}
// Step 9: After binary search, check if found is true
if (found) {
return true; // Return immediately if target is found
}
}
// Step 10: After checking all rows, return the final answer
return false; // Target does not exist in the matrix
};
// Driver code
const readline = require("readline");
const rl = readline.createInterface({
input: process.stdin,
output: process.stdout
});
let inputs = [];
let m = 0, n = 0, target = 0, rowCount = 0;
rl.on("line", function(line) {
if (inputs.length === 0) {
m = parseInt(line.trim()); // Input the number of rows
inputs.push(m);
} else if (inputs.length === 1) {
n = parseInt(line.trim()); // Input the number of columns
inputs.push(n);
} else if (inputs.length === 2) {
target = parseInt(line.trim()); // Input the target number
inputs.push(target);
} else {
let row = line.trim().split(' ').map(Number); // Input each row as space-separated integers
inputs.push(row);
rowCount++;
if (rowCount === m) {
let matrix = inputs.slice(3); // Extract the matrix part
let ans = searchMatrix(matrix, target);
console.log(ans ? "true" : "false"); // Output whether the target exists in the matrix
rl.close();
}
}
});
Time Complexity: O(m × log n)
Let us denote:
m = number of rows in the matrix
n = number of columns in the matrix
Initialization:
– We first get the number of rows m and the number of columns n using matrix.length and matrix[0].length.
– Time complexity: O(1) (constant time).
Loop Over Each Row:
– We use a for loop to iterate over each of the m rows.
– Number of iterations: m.
– Time complexity per iteration: depends on the binary search we perform next.
Binary Search in Each Row:
– Inside each row, we apply binary search to search for the target.
– Time complexity of binary search: O(log n).
– So, for each of the m rows: total time = O(log n).
Checking After Binary Search:
– After binary search, we check if found is true or false.
– This step is O(1).
Combining All Steps:
– Total time complexity: O(m) × O(log n) = O(m × log n).
Space Complexity: O(m × n)
Let us denote:
m = number of rows in the matrix
n = number of columns in the matrix
Auxiliary Space Complexity:
Definition: The extra space or temporary space used by the algorithm during its execution, excluding the input data.
Code Analysis:
The given code uses only a few variables:
– m and n for storing the number of rows and columns.
– found as a Boolean variable to indicate if the target is found.
– Loop variables like i, start, end, and mid during binary search.
All these variables take constant space (O(1)), independent of the input size.
Auxiliary Space Complexity: O(1)
Total Space Complexity:
The overall space used by the algorithm includes both the input data and the auxiliary space.
Input Data:
The input matrix itself is a 2D array with m rows and n columns, so it requires space proportional to its size: O(m × n).
Auxiliary Space: As analyzed above, O(1).
Combining Both:
Total space complexity: O(m × n) + O(1) = O(m × n).
Is the better approach efficient?
Given the problem constraints where the matrix dimensions satisfy 1 ≤ m, n ≤ 300, the binary search approach is also very practical.
Even though the method applies binary search on each row with time complexity O(m × log n), the total number of operations becomes at most 300 × log₂300 ≈ 300 × 8 = 2400, which is extremely fast for modern computers.
Since m and n are relatively small, this approach remains efficient and easy to implement while taking advantage of the sorted property of each row.
Therefore, despite the overhead of binary search logic, the solution runs comfortably within time limits and works reliably in practice.
The binary search approach works well, but can we do even better?
Since each row and column in the matrix is sorted in ascending order, we can cleverly use these properties to skip large parts of the search space.
Starting from the top-right or bottom-left corner, we can move only left or down (or up and right) based on comparisons with the target, reducing unnecessary checks. Lets see how!
Optimal Approach
Intuition
We’ve seen that binary search in each row works well by using the sorted property of rows, but it still searches each row separately.
Can we do better by using the fact that both rows and columns are sorted?
If we look carefully, the matrix is sorted in two directions: left to right and top to bottom.
This gives us more information to decide which parts of the matrix we can skip entirely.
Key observations:
Since each row is sorted left to right and each column is sorted top to bottom, if we look at a cell and it’s greater than the target, then everything below in that column must also be greater.
Similarly, if the cell is smaller than the target, everything to the left in that row must also be smaller.
How to use these observations:
We start at the top-right corner of the matrix with row = 0 and col = n - 1.
Then, as we move through the matrix:
– If the current cell equals the target, we immediately return true.
– If the current cell is greater than the target, then the target can’t be anywhere below in this column (since those numbers are even larger), so we move left (col--).
– If the current cell is smaller than the target, the target can’t be anywhere to the left in this row (since those numbers are even smaller), so we move down (row++).
Why this works efficiently:
In total, we can move down up to m times (once for each row) and move left up to n times (once for each column).
So the total number of steps is at most m + n.
We never revisit the same cell, and we always use the sorted property to decide where to go next.
Intuitive example:
Imagine starting at the top-right corner and trying to “walk” toward the target.
If the current number is too big, we move left; if it’s too small, we move down.
This way, we efficiently narrow the search space without scanning every cell.
Approach
Step 1: Start from the top‑right corner of the matrix
Initialize two pointers:
– row = 0 (first row)
– col = n – 1 (last column, where n is the number of columns)
We start here because this position allows us to:
- Move left if the number is too large
- Move down if it’s too small
Step 2: Loop while row is within the grid and col is non‑negative
Continue as long as:
- row < m (where m is the number of rows)
- col ≥ 0
Step 3: Check the current element at (row, col)
If matrix[row][col] == target:
- We have found the target number
Step 4: Return true immediately
Since the target exists in the matrix, return true
Step 5: If the current element is greater than target
Else if matrix[row][col] > target:
- The current element is too large
- Move left by decrementing: col = col – 1
Step 6: If the current element is smaller than target
Else (meaning matrix[row][col] < target):
- The current element is too small
- Move down by incrementing: row = row + 1
Step 7: After loop, return false if target not found
If we finish the loop without finding the target, return false to indicate the target does not exist in the matrix.
Let us understand with this video,
Dry Run
Let’s do a detailed dry run of the above approach
for the input: matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 20
Step 1: Understand the matrix
Original matrix:
Row 0 → [1, 4, 7, 11, 15]
Row 1 → [2, 5, 8, 12, 19]
Row 2 → [3, 6, 9, 16, 22]
Row 3 → [10, 13, 14, 17, 24]
Row 4 → [18, 21, 23, 26, 30]
Number of rows (m) = 5
Number of columns (n) = 5
We don’t need a count variable here because we just want to check if target=20 is present.
We start from the top-right corner: row=0, col=4
Iteration-wise dry run
row=0, col=4 → matrix[0][4]=15
target=20 > 15 → target is larger
Move down: row=1
row=1, col=4 → matrix[1][4]=19
target=20 > 19 → still larger
Move down: row=2
row=2, col=4 → matrix[2][4]=22
target=20 < 22 → too large
Move left: col=3
row=2, col=3 → matrix[2][3]=16
target=20 > 16 → too small
Move down: row=3
row=3, col=3 → matrix[3][3]=17
target=20 > 17 → still smaller
Move down: row=4
row=4, col=3 → matrix[4][3]=26
target=20 < 26 → too large
Move left: col=2
row=4, col=2 → matrix[4][2]=23
target=20 < 23 → still too large
Move left: col=1
row=4, col=1 → matrix[4][1]=21
target=20 < 21 → still too large
Move left: col=0
row=4, col=0 → matrix[4][0]=18
target=20 > 18 → too small
Move down: row=5 (out of bounds)
Final result
We have moved out of the grid without finding the target.
Conclusion: target=20 is not found in the matrix → return false.
Code for All Languages
C++
#include <iostream> // For input and output
#include <vector> // For using vector
using namespace std;
class Solution {
public:
bool searchMatrix(vector<vector<int>>& matrix, int target) {
int m = matrix.size(); // Number of rows
int n = matrix[0].size(); // Number of columns
// Step 1: Start from the top‑right corner of the matrix
// Initialize two pointers:
// – row = 0 (first row)
// – col = n – 1 (last column)
// We start here because this position allows us to:
// Move left if the number is too large
// Move down if it’s too small
int row = 0;
int col = n - 1;
// Step 2: Loop while row is within the grid and col is non‑negative
// Continue as long as:
// row < m (where m is the number of rows)
// col ≥ 0
while (row < m && col >= 0) {
// Step 3: Check the current element at (row, col)
if (matrix[row][col] == target) {
// We have found the target number
// Step 4: Return true immediately
// Since the target exists in the matrix, return true
return true;
}
// Step 5: If the current element is greater than target
else if (matrix[row][col] > target) {
// The current element is too large
// Move left by decrementing: col = col – 1
col--;
}
// Step 6: If the current element is smaller than target
else {
// The current element is too small
// Move down by incrementing: row = row + 1
row++;
}
}
// Step 7: After loop, return false if target not found
// If we finish the loop without finding the target, return false to indicate the target does not exist in the matrix
return false;
}
};
int main() {
int m, n, target;
cin >> m >> n >> target; // Input number of rows, columns, and target
vector<vector<int>> matrix(m, vector<int>(n));
// Input the matrix elements
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
cin >> matrix[i][j];
}
}
Solution sol;
bool result = sol.searchMatrix(matrix, target);
// Output the result
if (result) {
cout << "true" << endl;
} else {
cout << "false" << endl;
}
return 0;
}
Java
import java.util.*; // For Scanner
class Solution {
public boolean searchMatrix(int[][] matrix, int target) {
int m = matrix.length; // Number of rows
int n = matrix[0].length; // Number of columns
// Step 1: Start from the top‑right corner of the matrix
// Initialize two pointers:
// – row = 0 (first row)
// – col = n – 1 (last column)
// We start here because this position allows us to:
// Move left if the number is too large
// Move down if it’s too small
int row = 0;
int col = n - 1;
// Step 2: Loop while row is within the grid and col is non‑negative
// Continue as long as:
// row < m (where m is the number of rows)
// col ≥ 0
while (row < m && col >= 0) {
// Step 3: Check the current element at (row, col)
if (matrix[row][col] == target) {
// We have found the target number
// Step 4: Return true immediately
// Since the target exists in the matrix, return true
return true;
}
// Step 5: If the current element is greater than target
else if (matrix[row][col] > target) {
// The current element is too large
// Move left by decrementing: col = col – 1
col--;
}
// Step 6: If the current element is smaller than target
else {
// The current element is too small
// Move down by incrementing: row = row + 1
row++;
}
}
// Step 7: After loop, return false if target not found
// If we finish the loop without finding the target, return false to indicate the target does not exist in the matrix
return false;
}
}
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
// Input number of rows, columns, and target
int m = sc.nextInt();
int n = sc.nextInt();
int target = sc.nextInt();
int[][] matrix = new int[m][n];
// Input the matrix elements
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
matrix[i][j] = sc.nextInt();
}
}
Solution sol = new Solution();
boolean result = sol.searchMatrix(matrix, target);
// Output the result
System.out.println(result ? "true" : "false");
}
}
Python
from typing import List # For specifying the return type
class Solution:
def searchMatrix(self, matrix: List[List[int]], target: int) -> bool:
m = len(matrix) # Number of rows
n = len(matrix[0]) # Number of columns
# Step 1: Start from the top‑right corner of the matrix
# Initialize two pointers:
# – row = 0 (first row)
# – col = n – 1 (last column)
# We start here because this position allows us to:
# Move left if the number is too large
# Move down if it’s too small
row = 0
col = n - 1
# Step 2: Loop while row is within the grid and col is non‑negative
# Continue as long as:
# row < m (where m is the number of rows)
# col ≥ 0
while row < m and col >= 0:
# Step 3: Check the current element at (row, col)
if matrix[row][col] == target:
# We have found the target number
# Step 4: Return true immediately
# Since the target exists in the matrix, return true
return True
# Step 5: If the current element is greater than target
elif matrix[row][col] > target:
# The current element is too large
# Move left by decrementing: col = col – 1
col -= 1
# Step 6: If the current element is smaller than target
else:
# The current element is too small
# Move down by incrementing: row = row + 1
row += 1
# Step 7: After loop, return false if target not found
# If we finish the loop without finding the target, return false to indicate the target does not exist in the matrix
return False
# Driver Code
if __name__ == "__main__":
m = int(input()) # Input the number of rows
n = int(input()) # Input the number of columns
target = int(input()) # Input the target value
matrix = []
for _ in range(m):
row = list(map(int, input().split())) # Input each row as space-separated integers
matrix.append(row)
sol = Solution()
ans = sol.searchMatrix(matrix, target)
print("true" if ans else "false") # Output whether the target exists in the matrix
Javascript
/**
* @param {number[][]} matrix - 2D array representing the matrix of numbers
* @param {number} target - The target number to search for
* @return {boolean} - Whether the target exists in the matrix
*/
var searchMatrix = function(matrix, target) {
const m = matrix.length; // Number of rows
const n = matrix[0].length; // Number of columns
// Step 1: Start from the top‑right corner of the matrix
// Initialize two pointers:
// – row = 0 (first row)
// – col = n – 1 (last column)
// We start here because this position allows us to:
// Move left if the number is too large
// Move down if it’s too small
let row = 0;
let col = n - 1;
// Step 2: Loop while row is within the grid and col is non‑negative
// Continue as long as:
// row < m (number of rows)
// col ≥ 0
while (row < m && col >= 0) {
// Step 3: Check the current element at (row, col)
if (matrix[row][col] === target) {
// We have found the target number
// Step 4: Return true immediately
// Since the target exists in the matrix, return true
return true;
}
// Step 5: If the current element is greater than target
else if (matrix[row][col] > target) {
// The current element is too large
// Move left by decrementing: col = col – 1
col--;
}
// Step 6: If the current element is smaller than target
else {
// The current element is too small
// Move down by incrementing: row = row + 1
row++;
}
}
// Step 7: After loop, return false if target not found
// If we finish the loop without finding the target, return false
return false;
};
// Driver code
const readline = require("readline");
const rl = readline.createInterface({
input: process.stdin,
output: process.stdout
});
let inputs = [];
let m = 0, n = 0, target = 0, rowCount = 0;
rl.on("line", function(line) {
if (inputs.length === 0) {
m = parseInt(line.trim()); // Input number of rows
inputs.push(m);
} else if (inputs.length === 1) {
n = parseInt(line.trim()); // Input number of columns
inputs.push(n);
} else if (inputs.length === 2) {
target = parseInt(line.trim()); // Input target number
inputs.push(target);
} else {
let row = line.trim().split(' ').map(Number); // Input each row as space-separated integers
inputs.push(row);
rowCount++;
if (rowCount === m) {
let matrix = inputs.slice(3); // Extract matrix
let ans = searchMatrix(matrix, target);
console.log(ans ? "true" : "false"); // Output whether the target exists in the matrix
rl.close();
}
}
});
Time Complexity: O(m + n)
Let us denote:
– m = number of rows in the matrix
– n = number of columns in the matrix
Initialization:
– We first get the number of rows m and the number of columns n using matrix.length and matrix[0].length.
– Time complexity: O(1) (constant time).
Loop Traversal from Top‑Right Corner:
– We start from the top‑right corner and use a single while loop: while (row < m && col >= 0).
– At each step, we either move left (decrease col by 1) or move down (increase row by 1).
– The number of times we can move left is at most n (from last column to first).
– The number of times we can move down is at most m (from first row to last).
Total Number of Steps:
– We make at most m + n moves in total because each move strictly decreases col or increases row.
Combining All Steps:
– Total time complexity: O(m + n).
Space Complexity: O(m × n)
Let us denote:
– m = number of rows in the matrix
– n = number of columns in the matrix
Auxiliary Space Complexity:
Definition: The extra space or temporary space used by the algorithm during its execution, excluding the input data.
Code Analysis:
The given code uses only a few variables:
– m and n for storing the number of rows and columns.
– row and col as pointers to traverse the matrix.
All these variables take constant space, i.e., O(1), independent of the input size.
Auxiliary Space Complexity: O(1)
Total Space Complexity:
The overall space used by the algorithm includes both the input data and the auxiliary space.
Input Data:
The input matrix itself is a 2D array with m rows and n columns, so it requires space proportional to its size: O(m × n).
Auxiliary Space: As analyzed above, O(1).
Combining Both:
Total space complexity: O(m × n) + O(1) = O(m × n).
Learning Tip
Now we have successfully tackled this problem, let's try these similar problems.
You are given an m x n integer matrix matrix with the following two properties:
Each row is sorted in non-decreasing order.
The first integer of each row is greater than the last integer of the previous row.
Given an integer target, return true if target is in matrix or false otherwise.