Redistribute Characters to Make All Strings Equal Solution In C++/Java/Python/JS
Problem Description
You are given an array of strings words (0-indexed).
In one operation, pick two distinct indices i and j, where words[i] is a non-empty string, and move any character from words[i] to any position in words[j].
Return true if you can make every string in words equal using any number of operations, and false otherwise.
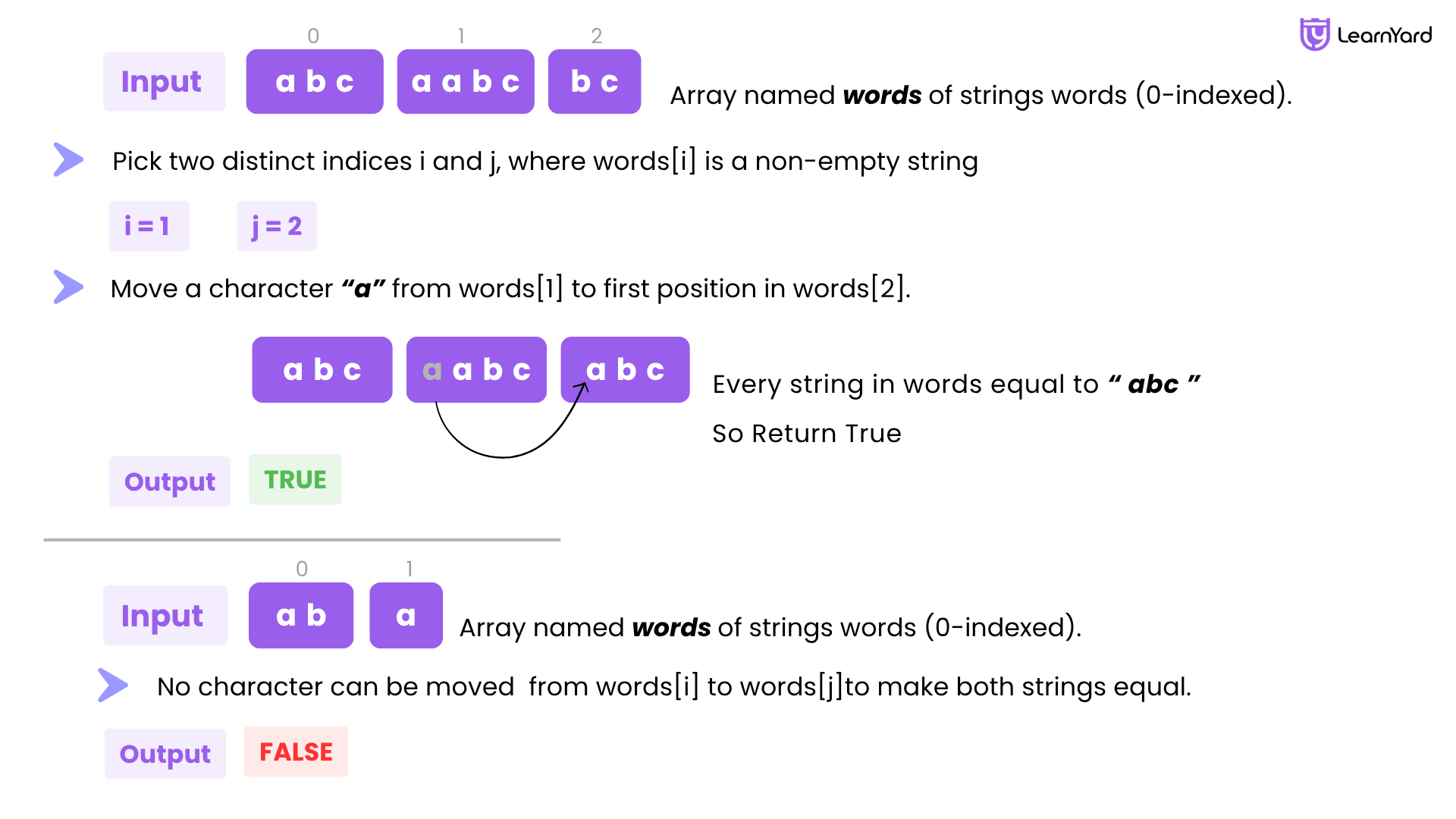
Example
Input: words = ["abc","aabc","bc"]
Output: true
Explanation: Move the first 'a' in words[1] to the front of words[2], to make words[1] = "abc" and words[2] = "abc".
All the strings are now equal to "abc", so return true.
Input: words = ["ab","a"]
Output: false
Explanation: It is impossible to make all the strings equal using the operation.
Constraints
- 1 <= words.length <= 100
- 1 <= words[i].length <= 100
- words[i] consists of lowercase English letters.
Figuring out "Redistribute Characters to Make All Strings Equal" can be solved using different approaches. We will first figure out the most intuitive approach and move to the optimal approach if exists. Let's sit with a pen and paper and figure out the algorithm !!
Optimal Approach
Intuition
We are given a list of strings. The task is to rearrange the characters among the strings—moving letters from one string to another—until all the strings become identical. Characters cannot be added or removed; they can only be moved between the strings. The goal is to determine whether it is possible to redistribute the letters so that every string ends up exactly the same.
Let’s Walk Through an Example
Suppose we're given: ["abc", "aabc", "bc"]
At first glance, they’re all different. But what if we took an a from the second string, and moved it to the third one?
Now they all look like "abc". And we’re done.
So that worked. But why?
Let’s try to make sense of it.
First Step: What’s Obvious?
One thing we can all agree on: Since we’re only moving characters around — never adding or deleting — the total number of each character stays the same.
So whatever letters we have at the beginning, that’s all we get. We’re just allowed to rearrange.
That leads to a natural question: If every string has to become identical, then... shouldn’t they all end up with the same characters in the same quantities?
Of course. And that means: Each letter must be evenly distributed across all strings.
If there are 3 strings and 6 total a’s, then each string must end up with exactly 2 a's.
But how do we figure that out?
How do we check if the letters can be split evenly?
Okay, But What About the Rest?
To answer that, we need to count how many times each character appears across the entire list of strings.
And that brings up a new question: How do we track character frequencies?
We could jot them down manually. But let’s be honest — we need something better. Something that lets us:
- Scan each word
- Go letter by letter
- Keep a running tally of how many times we’ve seen each character
Sounds like we need a system that lets us say:
“Hey, character 'a' — you’ve now been seen 4 times.”
That’s our clue.
How Do We Do That Efficiently?
We’re essentially describing a tool that stores:
- A key (the character)
- A value (how many times we’ve seen it)
That’s the job of a map.
Also known as a dictionary or hash map, depending on the language.
In other words:
- 'a' → 4
- 'b' → 3
- 'c' → 2
Every time we see a character, we bump its count by 1.
Then once we’ve counted everything, we check: Is the count of every character divisible by the number of strings?
If yes — we can evenly split them up. If not — it's impossible.
Can We Optimize This?
Here’s a follow-up question worth asking: Do we really need a full-fledged map?
Let’s pause and think.
What kind of keys are we storing?
Just lowercase letters — 'a' to 'z'. That’s only 26 possibilities. So instead of building a map that can store anything, why not just use a list (or array) with 26 slots?
Each slot represents a character:
- Index 0 → 'a'
- Index 1 → 'b'
- ...
- Index 25 → 'z'
Whenever we see a letter, we just update the value at the corresponding index.It’s fast. It’s clean. It’s all we need.
Is This Overkill?
In larger problems with a huge range of values — sure, we’d use maps. But here? With just 26 fixed characters?
A simple array gives us everything we want. Just direct indexing. This is an example of choosing the right tool for a specific job, not the most general one.
Let’s summarize the approach we’ve discovered:
- Count the total frequency of each character across all strings.
- Check whether each character’s total count is divisible by the number of strings.
- If every character passes the test, we can redistribute the letters evenly.
- If even one character doesn’t — there’s no way to make all strings equal.
Well summarized. Now, what kind of technique are we using here?
This is hashing — we’re organizing our data in a way that lets us count quickly and check conditions efficiently.
Even though we never actually simulate the character moves, hashing lets us understand whether such a move is even possible. Sometimes, counting is all it takes.
Let's now see how our algorithm looks!
Redistribute Characters to Make All Strings Equal Algorithm
- We count all characters: We go through each string and count how many times each character appears across all strings.
- We note the total number of strings: Let’s store the number of strings as n.
- We check divisibility: For each character, we check if its total count is divisible by n.
- We validate the possibility: If any character’s count is not divisible by n, we return false — it’s impossible to make all strings equal.
- We confirm the solution: If all characters can be evenly divided, we return true — we can redistribute letters to make all strings identical.
- What we're really checking: We’re ensuring that each character can be evenly shared among the strings, with no leftovers.
Approach
- Preprocess Character Frequencies:
- Initialize a frequency map or array to count how many times each character appears across all strings.
- Let n be the total number of strings.
- Count Characters Across All Strings:
- For each string in the input list, iterate through its characters and update the character count in the frequency structure.
- Validate Even Distribution:
- For each character and its total frequency, check if the frequency is divisible by n.
- If any character's frequency is not divisible evenly, return false.
- Return the Result:
- If all characters pass the divisibility check, return true indicating the characters can be rearranged to make all strings equal.
Dry-Run
Input: words = ["cacid", "cid", "aida"]
Goal: Determine whether we can redistribute characters to make all strings identical using only character movements between strings (no adding or removing characters).
Explanation:
Step 1: Count Frequencies of All Characters
We take an array of size 26 (for letters a–z), initialized with zeros:
freq = [0] * 26
Then, we go through each word and each character, incrementing the corresponding index:
Traverse "cacid":
- 'c' → freq['c' - 'a'] → freq[2] += 1 → freq[2] = 1
- 'a' → freq[0] += 1 → freq[0] = 1
- 'c' → freq[2] += 1 → freq[2] = 2
- 'i' → freq[8] += 1 → freq[8] = 1
- 'd' → freq[3] += 1 → freq[3] = 1
Traverse "cid":
- 'c' → freq[2] += 1 → freq[2] = 3
- 'i' → freq[8] += 1 → freq[8] = 2
- 'd' → freq[3] += 1 → freq[3] = 2
Traverse "aida":
- 'a' → freq[0] += 1 → freq[0] = 2
- 'i' → freq[8] += 1 → freq[8] = 3
- 'd' → freq[3] += 1 → freq[3] = 3
- 'a' → freq[0] += 1 → freq[0] = 3
Final frequency array (only non-zero entries shown):
a (freq[0]) = 3
c (freq[2]) = 3
d (freq[3]) = 3
i (freq[8]) = 3
Step 2: Number of Strings, n = 3
We must check that every character’s total count is divisible by 3 so each string can get an equal share.
Step 3: Check Divisibility
Now we check:
- a = 3 % 3 = 0 → OK
- c = 3 % 3 = 0 → OK
- d = 3 % 3 = 0 → OK
- i = 3 % 3 = 0 → OK
All character counts are divisible by n = 3.
What This Means:
Each character can be evenly split among the 3 strings.
We have:
- 3 a's → 1 per string
- 3 c's → 1 per string
- 3 d's → 1 per string
- 3 i's → 1 per string
Each string can be rearranged (or characters moved across) to become "acid", "daci", or any other permutation of the same letters.
Final Answer: true
Redistribute Characters to Make All Strings Equal Solution
Now let's checkout the "Redistribute Characters to Make All Strings Equal code" in C++, Java, Python and JavaScript.
"Redistribute Characters to Make All Strings Equal" Code in all Languages.
1. Redistribute Characters to Make All Strings Equal solution in C++ Try on Compiler
class Solution {
public:
bool makeEqual(vector<string>& words) {
// Frequency array to count characters
vector<int> counts(26, 0);
// Count frequency of each character across all words
for (const string& word : words) {
for (char c : word) {
counts[c - 'a']++;
}
}
// Get total number of words
int n = words.size();
// Check if each character count is divisible by number of words
for (int val : counts) {
if (val % n != 0) {
return false;
}
}
// All characters are evenly distributable
return true;
}
};2. Redistribute Characters to Make All Strings Equal Solution in Java Try on Compiler
public class Solution {
public boolean makeEqual(String[] words) {
// Frequency array to count characters
int[] counts = new int[26];
// Count frequency of each character across all words
for (String word : words) {
for (char c : word.toCharArray()) {
counts[c - 'a']++;
}
}
// Get total number of words
int n = words.length;
// Check if each character count is divisible by number of words
for (int val : counts) {
if (val % n != 0) {
return false;
}
}
// All characters are evenly distributable
return true;
}
}3. Redistribute Characters to Make All Strings Equal Solution in Python Try on Compiler
class Solution:
def makeEqual(self, words: List[str]) -> bool:
# Frequency array to count characters
counts = [0] * 26
# Count frequency of each character across all words
for word in words:
for c in word:
counts[ord(c) - ord('a')] += 1
# Get total number of words
n = len(words)
# Check if each character count is divisible by number of words
for val in counts:
if val % n != 0:
return False
# All characters are evenly distributable
return True4. Redistribute Characters to Make All Strings Equal solution in JavaScript Try on Compiler
/**
* @param {string[]} words
* @return {boolean}
*/
var makeEqual = function(words) {
// Frequency array to count characters
let counts = new Array(26).fill(0);
// Count frequency of each character across all words
for (let word of words) {
for (let c of word) {
counts[c.charCodeAt(0) - 97]++;
}
}
// Get total number of words
let n = words.length;
// Check if each character count is divisible by number of words
for (let val of counts) {
if (val % n !== 0) {
return false;
}
}
// All characters are evenly distributable
return true;
};Redistribute Characters to Make All Strings Equal Complexity Analysis
Time Complexity: O(m)
The Find Occurrences of an Element in an Array algorithm involves two key operations:
- Counting Character Frequencies: We iterate over each word and then over each character in each word to update the frequency array.
→ Let m be the total number of characters across all words.
→ This step takes O(m) time. - Divisibility Check: We loop through the fixed-size array counts (of size 26) to check if each character count is divisible by the number of words n.
→ This step takes O(26) = O(1) time.
Overall Time Complexity: O(m + 1) = O(m)
Space Complexity: O(m)
Auxiliary Space Complexity: Auxiliary space refers to the extra space required by the algorithm excluding the input.
- Frequency array:
A fixed-size integer array counts[26] is used to track the occurrences of each character (from 'a' to 'z').
→ This takes O(26) = O(1) space. - Scalar variables:
Variables like n and loop counters are simple integers.
→ These take constant space → O(1).
→ Thus, the auxiliary space complexity is O(1).
Total Space Complexity:
- Input array (words) is given → O(m), where m is the total number of characters across all words.
- Additional space (frequency array + variables) → O(1)
Hence, the total space complexity is O(m).
Similar Problems
Given two strings s and t, return true if t is an anagram of s, and false otherwise.
Given two strings ransomNote and magazine, return true if ransomNote can be constructed by using the letters from magazine and false otherwise.
Each letter in magazine can only be used once in ransomNote.