Rectangle Area II Solution In C++/Java/Python/JS
Problem Description
You are given a 2D array of axis-aligned rectangles. Each rectangle[i] = [xi1, yi1, xi2, yi2] denotes the ith rectangle where (xi1, yi1) are the coordinates of the bottom-left corner, and (xi2, yi2) are the coordinates of the top-right corner.
Calculate the total area covered by all rectangles in the plane. Any area covered by two or more rectangles should only be counted once.
Return the total area. Since the answer may be too large, return it modulo 109 + 7.
Example
Input: rectangles = [[0,0,2,2],[1,0,2,3],[1,0,3,1]]
Output: 6
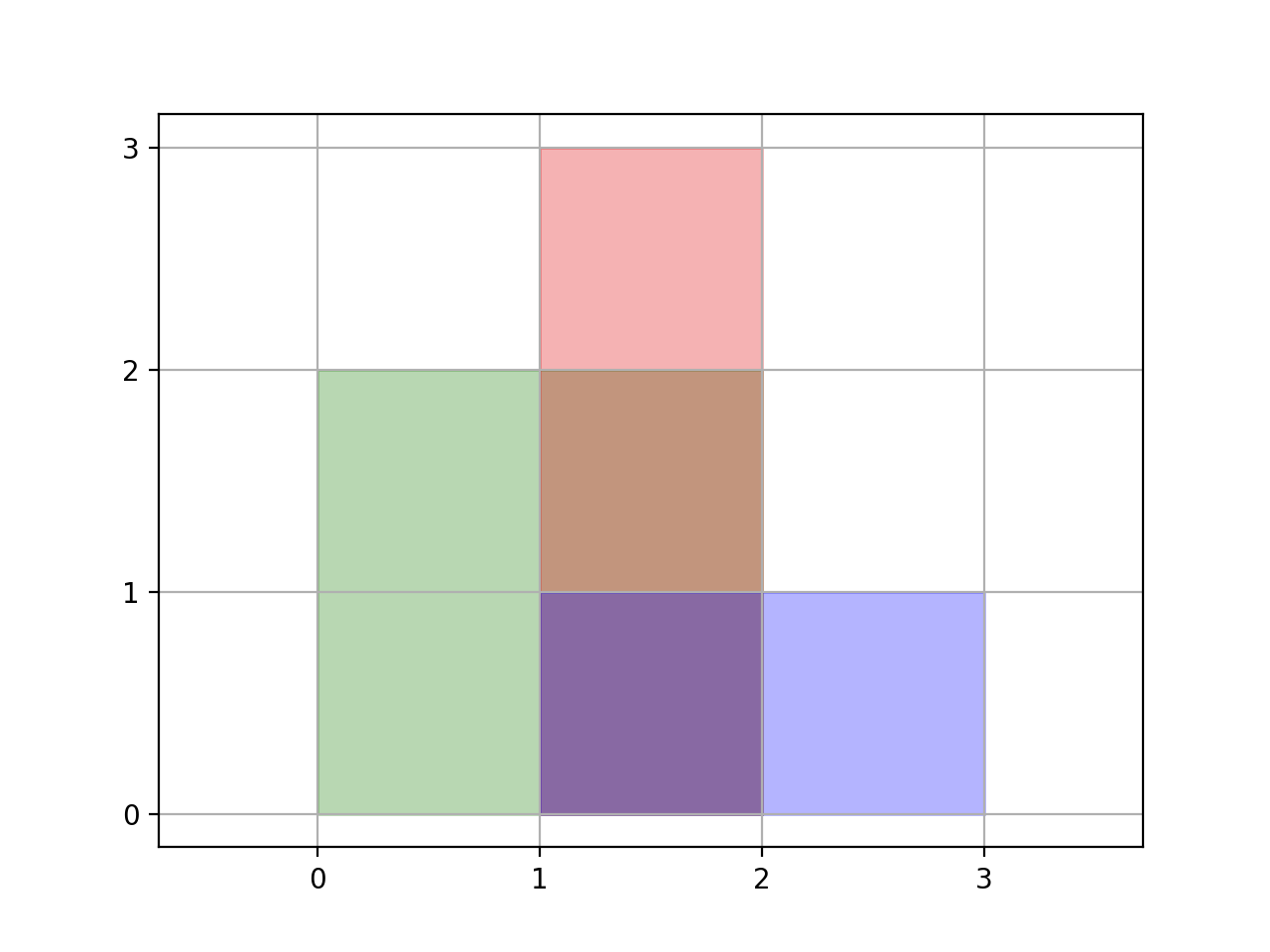
Explanation: A total area of 6 is covered by all three rectangles, as illustrated in the picture.
From (1,1) to (2,2), the green and red rectangles overlap.
From (1,0) to (2,3), all three rectangles overlap.
Input: rectangles = [[0,0,1000000000,1000000000]]
Output: 49
Explanation: The answer is 1018 modulo (109 + 7), which is 49.
Constraints
- 1 <= rectangles.length <= 200
- rectanges[i].length == 4
- 0 <= xi1, yi1, xi2, yi2 <= 109
- xi1 <= xi2
- yi1 <= yi2
- All rectangles have non zero area.
Figuring out "Rectangle Area II" can be solved using different approaches. We will first figure out the most intuitive approach and move to the optimal approach if exists. Let's sit with a pen and paper and figure out the algorithm !!
Optimal Approach
Intuition
We are given a set of axis-aligned rectangles on a two-dimensional plane, and our goal is to calculate the total area covered by these rectangles. Importantly, we must ensure that overlapping regions are only counted once in the total.
Let us take a structured approach to understanding and solving this problem.
Understanding the Problem
We are provided with:
- A list of rectangles, each defined by four coordinates: [x1, y1, x2, y2], which represent the bottom-left and top-right corners.
- The rectangles are axis-aligned, meaning all sides are either vertical or horizontal.
- If any rectangles overlap, their overlapping area must not be double-counted.
- Our objective is to compute the union area covered by all rectangles.
At first glance, this may seem straightforward. If there were no overlaps, we would simply compute the area of each rectangle and sum them:
Area = (x2 - x1) × (y2 - y1)
However, the presence of overlaps makes this more challenging. If we naively add the area of each rectangle, we may count some regions more than once.
Visualizing With an Example
Let us consider a concrete example:
rectangles = [
[1, 1, 3, 3], // Rectangle A
[2, 2, 4, 4], // Rectangle B
[3, 0, 5, 2] // Rectangle C
];
Breaking it down:
- Rectangle A spans from (1,1) to (3,3), forming a 2×2 square.
- Rectangle B spans from (2,2) to (4,4), another 2×2 square.
- Rectangle C spans from (3,0) to (5,2), a 2×2 rectangle below B.
Analyzing the overlaps:
- Rectangles A and B overlap in a 1×1 region.
- B and C are adjacent but do not overlap.
- A and C do not overlap at all.
If we sum the individual areas:
- A: 4 units
- B: 4 units
- C: 4 units
This gives us 12 units, but we have counted the 1×1 overlap between A and B twice. Therefore, the correct total area is 12 - 1 = 11 units.
Can We Simulate the Grid?
One potential approach is to simulate the entire grid and mark every point that is covered. While this is feasible for small values, it becomes impractical when the coordinate ranges are large—possibly up to a billion. Clearly, we need a more efficient strategy.
Step 4: Rethinking the Approach – Sweep Line Algorithm
Instead of simulating every point, let us consider sweeping a vertical line from left to right across the x-axis.
Here is the idea:
- At every x-coordinate where a rectangle starts or ends, we process an event.
- While sweeping, we keep track of the set of active rectangles at that x-position.
- For the current active rectangles, we compute the total length of y-intervals covered.
- The area covered between two x-positions is simply the vertical coverage multiplied by the horizontal distance moved.
- We accumulate these strip areas as we go.
This is the core of the sweep line technique, augmented by a segment tree to manage y-intervals efficiently.
Applying the Sweep Line on Our Example
We list all events in terms of vertical sides of the rectangles:
- At x = 1, rectangle A starts: covers y from 1 to 3.
- At x = 2, rectangle B starts: covers y from 2 to 4.
- At x = 3, rectangle A ends and rectangle C starts.
- At x = 4, rectangle B ends.
- At x = 5, rectangle C ends.
We sort these events by x-coordinate. At each step, we calculate the total y-length covered by the currently active rectangles, multiply it by the horizontal width since the previous x-coordinate, and add it to the total area.
Let us manually simulate the process:
- At x = 1:
- Only A is active, covering y from 1 to 3 → y-length = 2
- Next x = 2 → width = 1
- Area = 2 × 1 = 2
- At x = 2:
- A and B are active: intervals [1–3] and [2–4]
- Union of y-intervals = [1–4] → y-length = 3
- Width = 1 → Area = 3
- Cumulative area = 5
- At x = 3:
- A ends, C starts → Active: B [2–4], C [0–2]
- Union = [0–4] → y-length = 4
- Width = 1 → Area = 4
- Cumulative area = 9
- At x = 4:
- B ends → Only C remains: y = [0–2] → y-length = 2
- Width = 1 → Area = 2
- Final total = 11
This matches our earlier manual computation and validates our approach.
How Do We Efficiently Compute the Covered Y-Intervals?
Earlier, we established that at any given x-coordinate during the sweep, we know which rectangles are active—that is, those we have entered but not yet exited. The next challenge is determining the total vertical length (on the y-axis) that is covered by these active rectangles.
This is not as straightforward as summing intervals manually—especially for large inputs. When dealing with intervals such as [1, 3], [2, 4], or [0, 2], our goal is to compute the total length of their union without double-counting overlaps.
To solve this efficiently, we need a data structure that can:
- Add or remove a y-interval when a rectangle starts or ends.
- After each update, quickly answer: “What is the total y-length currently covered?”
This is where the Segment Tree becomes useful.
Introducing the Segment Tree
A segment tree is a tree-based data structure built to efficiently represent a continuous range—in this case, the y-axis.
- The root node covers the full range of y-values that we care about.
- Each internal node represents a subinterval of that range, splitting it recursively.
- The leaves correspond to the smallest atomic y-intervals between adjacent coordinate values.
The segment tree supports:
- Range updates: We can increment or decrement counts over subintervals (to reflect rectangles being added or removed).
- Coverage queries: At any moment, we can ask: “What is the total y-length currently covered by at least one rectangle?”
When we activate a rectangle, we increment the count in the tree for the corresponding y-interval. If multiple rectangles overlap, the count may exceed one—but for area calculation, we only care whether the count is greater than zero. When a rectangle ends, we decrement the same y-interval.
Thanks to the tree’s structure, both updates and queries are efficient—achieving logarithmic time relative to the number of unique y-coordinates.
A Simplified View: Explaining the Segment Tree Intuitively
Imagine we divide the y-axis into several subintervals: [0, 1], [1, 2], [2, 3], and so on.
- We construct a tree that connects these intervals hierarchically.
- Each segment keeps track of how many rectangles currently cover it (a count).
- If a segment has a positive count, we consider its full length as “covered.”
- The total y-length covered is the sum of all such fully-covered segments.
This way, we can compute vertical coverage at each x-step efficiently and precisely.
Applying the Segment Tree to Our Example
Let us revisit the rectangle input:
A: [1, 1] to [3, 3]
B: [2, 2] to [4, 4]
C: [3, 0] to [5, 2]
We previously calculated the area manually using y-interval merging. Now, let us imagine how the segment tree handles it automatically.
- Preprocessing: We extract and sort all unique y-values: {0, 1, 2, 3, 4}. We build the segment tree over the intervals: [0, 1], [1, 2], [2, 3], [3, 4].
- At x = 1:
- Rectangle A begins: we increment the count for [1, 3].
- The tree reports a total covered y-length of 2.
- At x = 2:
- Rectangle B begins: we increment the count for [2, 4].
- Now, overlapping intervals include [1, 4], with varying counts.
- The tree reports a total covered y-length of 3.
- At x = 3:
- Rectangle A ends: we decrement the count for [1, 3].
- Rectangle C begins: we increment the count for [0, 2].
- Coverage now spans [0, 4]; the total y-length covered is 4.
And so forth. At each step, the segment tree efficiently updates its internal state and reports the covered vertical length, eliminating the need for manual interval merging.
Recap of the Overall Process
To summarize the complete approach:
- Transform the problem into vertical strips between consecutive x-events (rectangle starts and ends).
- At each event:
- Update the y-interval in the segment tree: +1 when a rectangle starts, –1 when it ends.
- Query the total y-length currently covered (i.e., segments where count > 0).
- Multiply this by the width between the current and next x-event to compute the area of that vertical strip.
- Aggregate the results, and return the total area modulo 10^9 + 7.
Is This a Greedy Approach?
Yes, this qualifies as a greedy algorithm. At each step, we sweep from left to right and take the best available local contribution to the total area—without revisiting past decisions. However, this is not the typical "greedy selection" strategy. Rather, it is a geometric sweep that incrementally builds the answer by managing interval coverage intelligently.
The core insight is:
- We need to avoid double-counting overlaps.
- We realize a left-to-right sweep helps us process the plane incrementally.
- We use a segment tree to handle fast vertical interval updates and queries.
Once this structure is understood, the solution becomes both efficient and conceptually clean.
Let's now see how our algorithm looks!
Rectangle Area II Algorithm
We implement a Rectangle Area II solution using a greedy approach.
- We start by collecting all rectangle start and end events and all y-coordinates involved.
- We sort the y-values and assign them indices to allow efficient interval tracking.
- We build a segment tree to keep track of which y-intervals are currently covered and how much total y-length is covered.
- We sort all the rectangle events by x-coordinate so we can process them from left to right.
- As we move from one x-coordinate to the next:
- We calculate the area covered in that vertical slice.
- We update the active y-intervals based on which rectangles start or end.
- We sum up all the area slices and return the total modulo 10^9 + 7.
Approach
Initialize:
- Create an empty list events
- Create an empty set y_set to store all y-coordinates
Parse Rectangles:
- For each rectangle [x1, y1, x2, y2]:
- Add two events:
(x1, 1, y1, y2) → rectangle starts
(x2, -1, y1, y2) → rectangle ends - Add y1 and y2 to y_set
- Add two events:
Coordinate Compression:
- Sort y_set and store as sorted_y
- Create a map: y_i = {y: i for i, y in enumerate(sorted_y)}
(used to index into segment tree)
Build Segment Tree:
- Build a segment tree over intervals [0, len(sorted_y) - 2]
- Each leaf represents interval [y[i], y[i+1]]
- Each node tracks:
- count: how many rectangles cover it
- total: total length covered
Sort Events: Sort events by x
Sweep Line Loop:
- Initialize prev_x = 0, area = 0
- For each (x, typ, y1, y2) in events:
- Compute dx = x - prev_x
- Get current covered_y = segment_tree.total
- Add dx * covered_y to area
- Update segment tree with [y_i[y1], y_i[y2]], using typ (+1 or -1)
- Set prev_x = x
Return: Return area % (10^9 + 7)
Dry-Run
Input: Rectangles:
A = [0, 0, 2, 2]
B = [1, 1, 3, 3]
C = [3, 0, 4, 1]
D = [0, 3, 1, 4]
Explanation
Step 1: Create events
Each rectangle gives 2 events (start and end):
[0, 0, 2, +1] → A enters
[2, 0, 2, -1] → A exits
[1, 1, 3, +1] → B enters
[3, 1, 3, -1] → B exits
[3, 0, 1, +1] → C enters
[4, 0, 1, -1] → C exits
[0, 3, 4, +1] → D enters
[1, 3, 4, -1] → D exits
Step 2: Sort events by x (sweep order)
Sorted:
[0, 0, 2, +1] → A enters
[0, 3, 4, +1] → D enters
[1, 1, 3, +1] → B enters
[1, 3, 4, -1] → D exits
[2, 0, 2, -1] → A exits
[3, 1, 3, -1] → B exits
[3, 0, 1, +1] → C enters
[4, 0, 1, -1] → C exits
Step 3: Sweep and compute area
We maintain a set of active y-intervals and calculate vertical coverage at each step.
Start:
- prev_x = 0
- total_area = 0
- active = empty
x = 0, events:
- Add [0,2] (A enters)
- Add [3,4] (D enters)
→ Active intervals: [0,2], [3,4]
→ Union y-length = 2 + 1 = 3
→ Width = 1 (next x is 1)
→ Area += 3 × 1 = 3
→ total_area = 3
x = 1, events:
- Add [1,3] (B enters)
- Remove [3,4] (D exits)
→ Active: [0,2], [1,3]
→ Union: [0,3]
→ y-length = 3
→ Width = 1
→ Area += 3 × 1 = 3
→ total_area = 6
x = 2, events:
- Remove [0,2] (A exits)
→ Active: [1,3]
→ y-length = 2
→ Width = 1
→ Area += 2 × 1 = 2
→ total_area = 8
x = 3, events:
- Remove [1,3] (B exits)
- Add [0,1] (C enters)
→ Active: [0,1]
→ y-length = 1
→ Width = 1
→ Area += 1 × 1 = 1
→ total_area = 9
x = 4, events:
- Remove [0,1] (C exits)
→ Active: empty
→ y-length = 0
→ Width = 0
→ Area += 0
→ total_area = 9
Final Answer: Total Union Area = 9
Rectangle Area II Solution
Now let's checkout the "Rectangle Area II" in C++, Java, Python and JavaScript.
"Rectangle Area II" Code in all Languages.
1. Rectangle Area II solution in C++ Try on Compiler
class Solution {
public:
int rectangleArea(vector<vector<int>>& rectangles) {
const int MOD = 1e9 + 7;
// Step 1: Collect all y-coordinates for coordinate compression
vector<int> ys;
vector<tuple<int, int, int, int>> events;
for (auto& rect : rectangles) {
int x1 = rect[0], y1 = rect[1], x2 = rect[2], y2 = rect[3];
// Add start and end x events
// type = 1 (rectangle start)
events.emplace_back(x1, y1, y2, 1);
// type = -1 (rectangle end)
events.emplace_back(x2, y1, y2, -1);
ys.push_back(y1);
ys.push_back(y2);
}
// Step 2: Coordinate compression for y-values
sort(ys.begin(), ys.end());
ys.erase(unique(ys.begin(), ys.end()), ys.end());
map<int, int> yToIdx;
for (int i = 0; i < ys.size(); ++i) {
yToIdx[ys[i]] = i;
}
// Step 3: Sort events by x-coordinate
sort(events.begin(), events.end());
int n = ys.size();
// count[i] = how many times segment [i, i+1] is covered
vector<int> count(4 * n), length(4 * n);
// Step 4: Segment Tree Update function (recursive lambda)
auto update = [&](auto&& self, int node, int l, int r, int ul, int ur, int val) -> void {
if (ur <= l || r <= ul) return;
if (ul <= l && r <= ur) {
count[node] += val;
} else {
int m = (l + r) / 2;
self(self, 2 * node, l, m, ul, ur, val);
self(self, 2 * node + 1, m, r, ul, ur, val);
}
if (count[node] > 0) {
length[node] = ys[r] - ys[l];
} else if (r - l == 1) {
length[node] = 0;
} else {
length[node] = length[2 * node] + length[2 * node + 1];
}
};
long long area = 0;
// Step 5: Line sweep through x-events
for (int i = 0; i < events.size(); ++i) {
auto [x, y1, y2, type] = events[i];
if (i > 0) {
int prevX = get<0>(events[i - 1]);
long long width = x - prevX;
long long height = length[1];
area = (area + width * height) % MOD;
}
// Update y-range [y1, y2) with +1 or -1
update(update, 1, 0, n - 1, yToIdx[y1], yToIdx[y2], type);
}
return area;
}
};2. Rectangle Area II Solution in Java Try on Compiler
class Solution {
public int rectangleArea(int[][] rectangles) {
// MOD value
final int MOD = 1_000_000_007;
// Collect all y-coordinates
TreeSet<Integer> yCoords = new TreeSet<>();
List<int[]> events = new ArrayList<>();
for (int[] r : rectangles) {
yCoords.add(r[1]);
yCoords.add(r[3]);
events.add(new int[]{r[0], 1, r[1], r[3]});
events.add(new int[]{r[2], -1, r[1], r[3]});
}
// Compress y values
List<Integer> ysList = new ArrayList<>(yCoords);
Map<Integer, Integer> yToIdx = new HashMap<>();
for (int i = 0; i < ysList.size(); ++i)
yToIdx.put(ysList.get(i), i);
// Segment tree data
int[] count = new int[ysList.size() * 4];
int[] length = new int[ysList.size() * 4];
// Sort events by x
events.sort(Comparator.comparingInt(a -> a[0]));
// Segment tree update
class SegmentTree {
void update(int node, int l, int r, int ul, int ur, int val) {
if (ur <= l || r <= ul) return;
if (ul <= l && r <= ur) {
count[node] += val;
} else {
int m = (l + r) / 2;
update(2 * node, l, m, ul, ur, val);
update(2 * node + 1, m, r, ul, ur, val);
}
if (count[node] > 0) {
length[node] = ysList.get(r) - ysList.get(l);
} else if (r - l == 1) {
length[node] = 0;
} else {
length[node] = length[2 * node] + length[2 * node + 1];
}
}
}
SegmentTree st = new SegmentTree();
long area = 0;
int prevX = events.get(0)[0];
for (int[] e : events) {
// Compute area for x-span
area += 1L * length[1] * (e[0] - prevX);
area %= MOD;
// Update segment tree
st.update(1, 0, ysList.size() - 1, yToIdx.get(e[2]), yToIdx.get(e[3]), e[1]);
prevX = e[0];
}
return (int) area;
}
}3. Rectangle Area II Solution in Python Try on Compiler
class Solution:
def rectangleArea(self, rectangles):
# MOD value
MOD = 10 ** 9 + 7
# Collect all y-coordinates
ys = set()
events = []
for x1, y1, x2, y2 in rectangles:
ys.update([y1, y2])
events.append((x1, 1, y1, y2))
events.append((x2, -1, y1, y2))
# Coordinate compression
ys = sorted(ys)
y_id = {v: i for i, v in enumerate(ys)}
# Initialize segment tree arrays
count = [0] * (len(ys) * 4)
length = [0] * (len(ys) * 4)
# Update segment tree
def update(node, l, r, ul, ur, val):
if ur <= l or r <= ul:
return
if ul <= l and r <= ur:
count[node] += val
else:
m = (l + r) // 2
update(node * 2, l, m, ul, ur, val)
update(node * 2 + 1, m, r, ul, ur, val)
if count[node] > 0:
length[node] = ys[r] - ys[l]
elif r - l == 1:
length[node] = 0
else:
length[node] = length[2 * node] + length[2 * node + 1]
# Sort events
events.sort()
prev_x = events[0][0]
res = 0
for x, typ, y1, y2 in events:
# Add area for the width strip
res += length[1] * (x - prev_x)
res %= MOD
# Update tree
update(1, 0, len(ys) - 1, y_id[y1], y_id[y2], typ)
prev_x = x
return res4. Rectangle Area II solution in JavaScript Try on Compiler
/**
* @param {number[][]} rectangles
* @return {number}
*/
var rectangleArea = function(rectangles) {
// Modulo for large number results
const MOD = 1_000_000_007;
// Step 1: Collect all unique y-coordinates and prepare events
const yCoords = new Set();
const events = [];
for (const r of rectangles) {
yCoords.add(r[1]);
yCoords.add(r[3]);
// Add start and end events for each rectangle
// Event format: [x, type (1 or -1), y1, y2]
events.push([r[0], 1, r[1], r[3]]);
events.push([r[2], -1, r[1], r[3]]);
}
// Step 2: Coordinate compression for y-coordinates
const ysList = Array.from(yCoords).sort((a, b) => a - b);
const yToIdx = new Map();
for (let i = 0; i < ysList.length; ++i) {
yToIdx.set(ysList[i], i);
}
// Segment tree arrays to maintain count and covered length
const count = new Array(ysList.length * 4).fill(0);
const length = new Array(ysList.length * 4).fill(0);
// Step 3: Segment Tree class to manage intervals efficiently
class SegmentTree {
update(node, l, r, ul, ur, val) {
// No overlap
if (ur <= l || r <= ul) return;
// Full coverage
if (ul <= l && r <= ur) {
count[node] += val;
} else {
// Partial coverage - recurse children
const m = Math.floor((l + r) / 2);
this.update(2 * node, l, m, ul, ur, val);
this.update(2 * node + 1, m, r, ul, ur, val);
}
// Update length covered at current node
if (count[node] > 0) {
length[node] = ysList[r] - ysList[l];
} else if (r - l === 1) {
length[node] = 0;
} else {
length[node] = length[2 * node] + length[2 * node + 1];
}
}
}
// Initialize segment tree
const st = new SegmentTree();
// Step 4: Process events sorted by x-coordinate
events.sort((a, b) => a[0] - b[0]);
let area = 0n; // BigInt for large area calculation
let prevX = events[0][0];
for (const e of events) {
// Add area covered since last event:
// width * current covered height
area = (area + BigInt(length[1]) * BigInt(e[0] - prevX)) % BigInt(MOD);
// Update segment tree with current event
st.update(1, 0, ysList.length - 1, yToIdx.get(e[2]), yToIdx.get(e[3]), e[1]);
prevX = e[0];
}
// Convert area back to Number to return
return Number(area);
};Rectangle Area II Complexity Analysis
Time Complexity: O(n log n)
The rectangle area union algorithm involves two major phases:
1. Event Generation and Coordinate Compression
- For n rectangles:
- Each contributes 2 events (start and end), so we create O(n) events.
- We collect 2 y-coordinates per rectangle (bottom and top), and then sort them: O(n log n).
- Coordinate compression:
- Sorting unique y-coordinates takes O(k log k), where k ≤ 2n.
- Mapping coordinates to indices is O(k).
🔹 Total time for this phase: O(n log n) (as k ≤ 2n ⇒ O(k log k) = O(n log n))
2. Event Processing Using Sweep Line + Segment Tree
- We sort 2n events by x-coordinate ⇒ O(n log n).
- For each of the 2n events:
- We do a segment tree update on a range of compressed y-values.
- Segment tree update/query takes O(log k) per event.
- The final area calculation occurs over these 2n events.
🔹 Total time for this phase: O(n log k) ⇒ As k ≤ 2n, this simplifies to O(n log n)
Total Time Complexity: Phase 1 (prep) + Phase 2 (sweep) = O(n log n) + O(n log n) = O(n log n)
Space Complexity: O(n)
Auxiliary Space Complexity: Auxiliary space refers to the extra space required by the algorithm excluding the input.
- Coordinate compression:
We extract and sort unique y-coordinates, stored in a list of size O(k), where k is the number of unique y-values. We also use a map yToIdx of size O(k). - Segment Tree Arrays:
We use two arrays count[] and length[], both of size O(4k) to support segment tree operations, where k is the number of unique y-values. - Events array:
We build a list of events from input rectangles; each rectangle adds two events, so for n rectangles, the array is size O(2n). - Miscellaneous variables:
Loop counters, BigInt area, and constant number of temporary variables are all O(1).
🔹 So, total auxiliary space = O(k + 4k + 2n + 1) = O(k + n), where k ≤ 2n.
⇒ Simplifies to: O(n).
Total Space Complexity: Total space includes both input and auxiliary:
- Input rectangles:
The input is a list of n rectangles, each with 4 integers ⇒ total input space = O(n). - Auxiliary space:
As shown above = O(n).
🔹 Total space complexity = O(n) + O(n) = O(n).
Similar Problems
You are given a 2D integer array squares. Each squares[i] = [xi, yi, li] represents the coordinates of the bottom-left point and the side length of a square parallel to the x-axis.
Find the minimum y-coordinate value of a horizontal line such that the total area covered by squares above the line equals the total area covered by squares below the line.
Answers within 10-5 of the actual answer will be accepted.
Note: Squares may overlap. Overlapping areas should be counted only once in this version.
There are some spherical balloons taped onto a flat wall that represents the XY-plane. The balloons are represented as a 2D integer array points where points[i] = [xstart, xend] denotes a balloon whose horizontal diameter stretches between xstart and xend. You do not know the exact y-coordinates of the balloons.
Arrows can be shot up directly vertically (in the positive y-direction) from different points along the x-axis. A balloon with xstart and xend is burst by an arrow shot at x if xstart <= x <= xend. There is no limit to the number of arrows that can be shot. A shot arrow keeps traveling up infinitely, bursting any balloons in its path.
Given the array points, return the minimum number of arrows that must be shot to burst all balloons.