Perfect Rectangle Solution In C++/Java/Python/JS
Given an array rectangles where rectangles[i] = [xi, yi, ai, bi] represents an axis-aligned rectangle. The bottom-left point of the rectangle is (xi, yi) and the top-right point of it is (ai, bi).
Return true if all the rectangles together form an exact cover of a rectangular region.
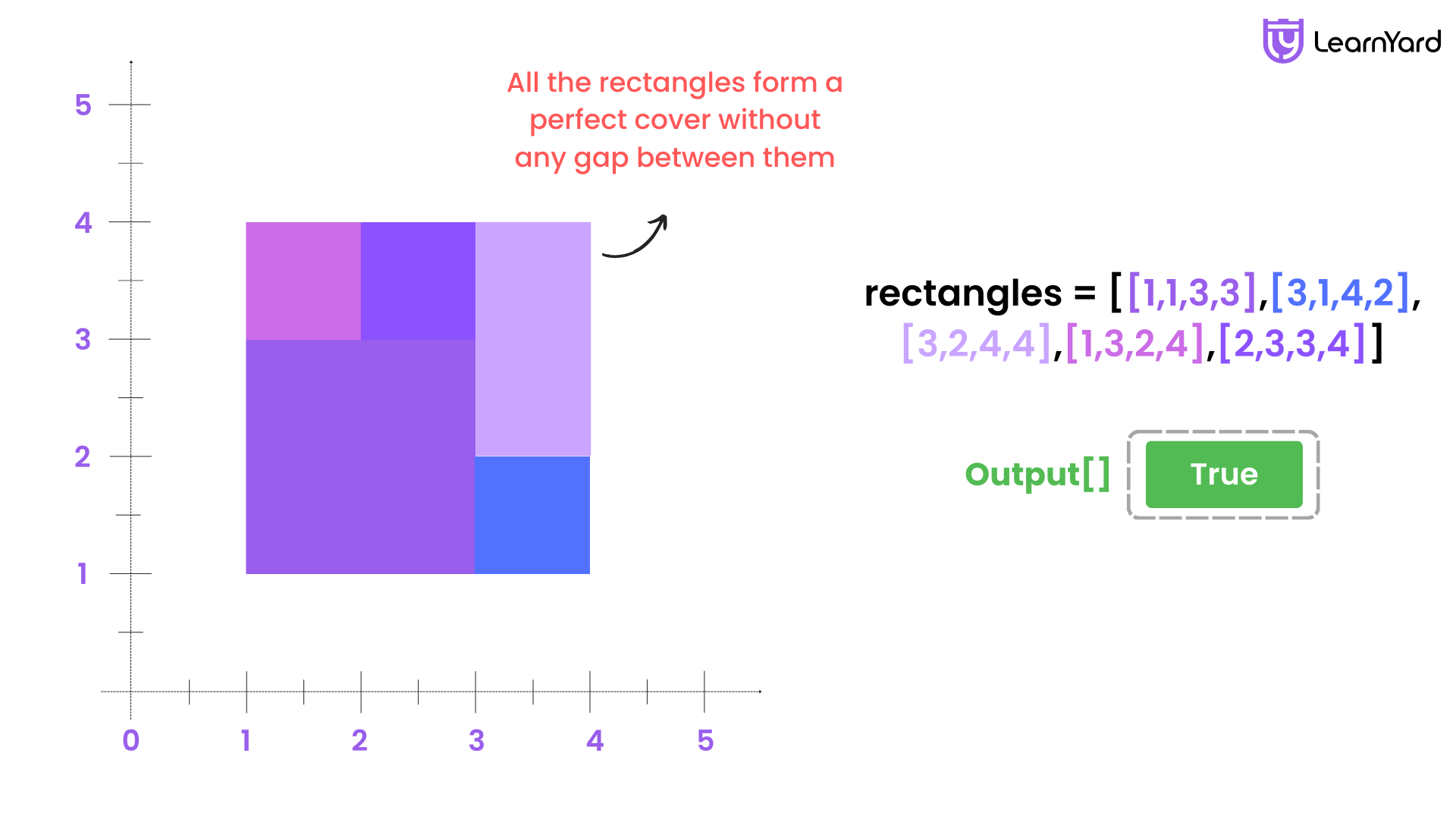
Example
Input: rectangles = [[1,1,3,3],[3,1,4,2],[3,2,4,4],[1,3,2,4],[2,3,3,4]]
Output: true
Explanation: All 5 rectangles together form an exact cover of a rectangular region.
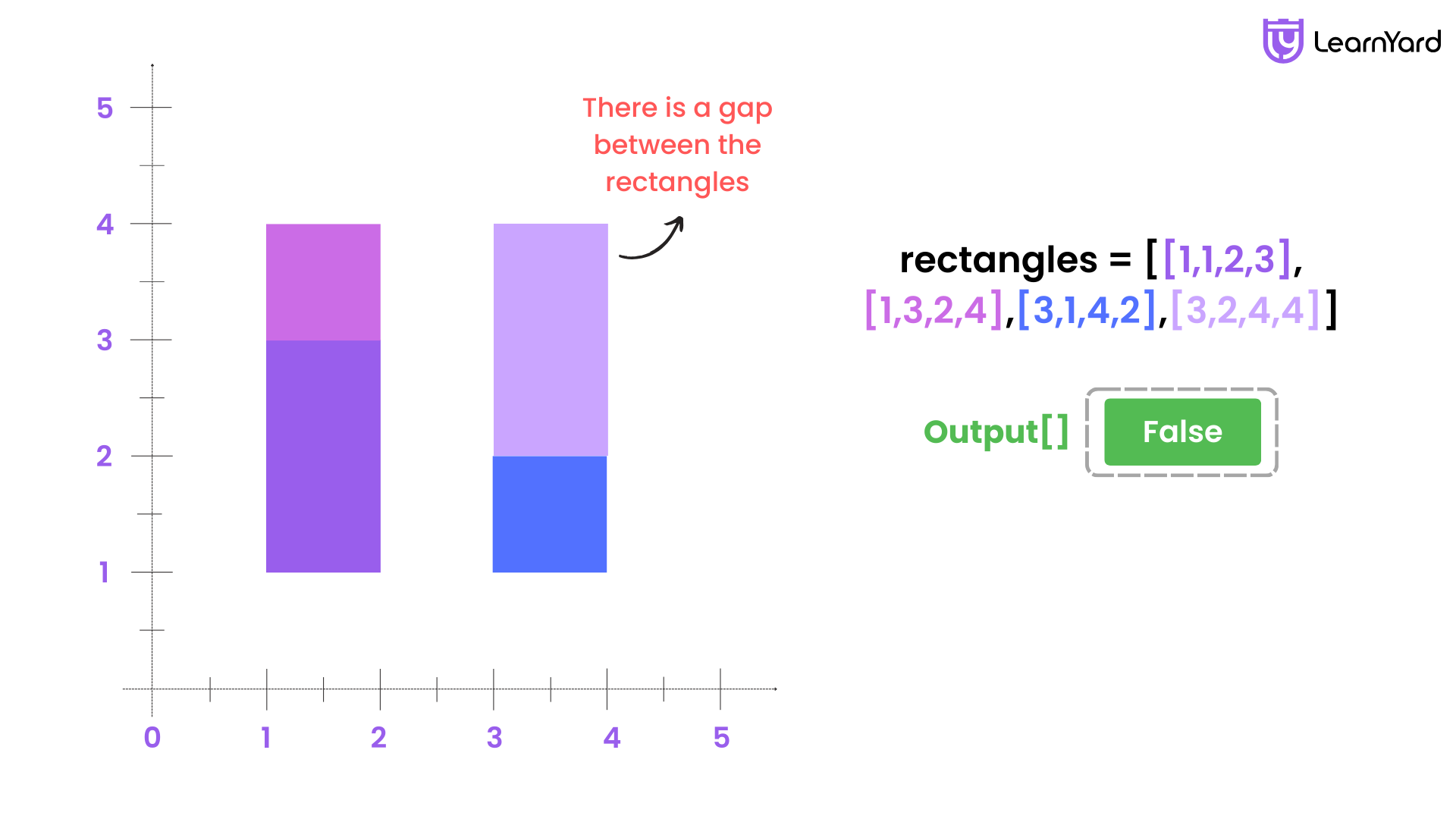
Input: rectangles = [[1,1,2,3],[1,3,2,4],[3,1,4,2],[3,2,4,4]]
Output: false
Explanation: Because there is a gap between the two rectangular regions.
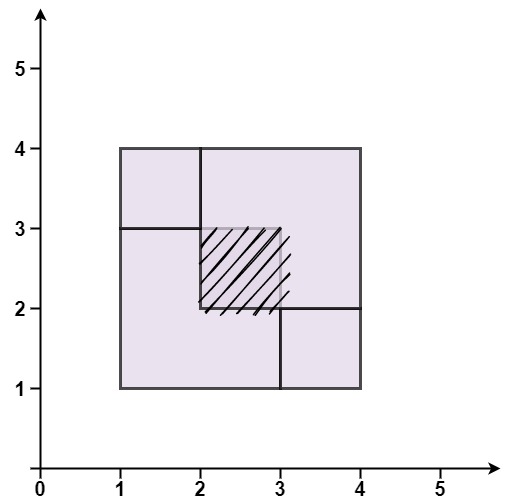
Input: rectangles = [[1,1,3,3],[3,1,4,2],[1,3,2,4],[2,2,4,4]]
Output: false
Explanation: Because two of the rectangles overlap with each other.
Constraints
- 1 <= rectangles.length <= 2 * 104
- rectangles[i].length == 4
- -105 <= xi < ai <= 105
- -105 <= yi < bi <= 105
Figuring out "Perfect Rectangle solution" can be solved using different approaches. We will first figure out the most intuitive approach and move to the optimal approach if exists. Let's sit with a pen and paper and figure out the algorithm !!
Optimal Approach
Intuition
Let’s try to solve this interesting rectangle puzzle together. We’re given a bunch of small rectangles, and each rectangle is represented by four numbers: [xi,yi,ai,bi]. These numbers define the bottom-left and top-right corners of that rectangle.
Now, the big question is: Can these rectangles perfectly fit together - like a jigsaw puzzle - without overlapping and without leaving any gaps, to form one big rectangle?"
how do we even check that?
Suppose we give you the following input:
rectangles = [
[1, 1, 3, 3],
[3, 1, 4, 2],
[3, 2, 4, 4],
[1, 3, 2, 4],
[2, 3, 3, 4]
]
Can we figure out whether these together make one big rectangle?
"Okay, first of all, if all the rectangles perfectly fit into a bigger rectangle, wouldn’t the total area of all these small rectangles have to equal the area of the big rectangle they are covering?"
"Yes, that makes sense. If there’s any extra overlap or a hole, the area would either be more or less."
"Exactly! So, first step - we compute the area of each small rectangle, and then also track the smallest and largest x and y values to form the outer bounding rectangle. Let’s do that!"
We go through each rectangle, and for every rectangle [x1,y1,x2,y2] we calculate its area: Area = (x2 - x1) * (y2 - y1)
And as we go, we keep track of the smallest x (minX), smallest y (minY), largest x (maxX), largest y (maxY). These define the bounding rectangle.
Also - this part is important—we track each corner point of each rectangle using a frequency counter (like a HashMap or defaultdict).
But wait—why are we tracking corner points?
Let us think about this: in a perfect cover with no overlaps or gaps, what can we say about the corners?
Let’s say these small rectangles build a perfect big rectangle. What do you think should happen to the corners of these rectangles?
Uhh… the four outer corners of the big rectangle should appear only once?
"Exactly! Those outermost points should only appear once because they’re not shared. Every other point - those that are internal - must be shared between either two or four rectangles."
That makes sense! Because if it appears three times, that must mean there's a problem - either a gap or an overlap.
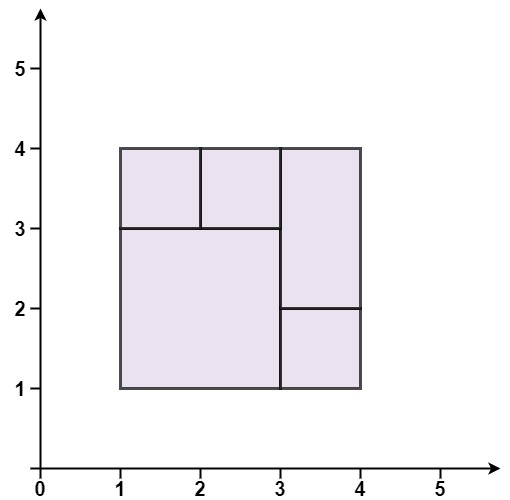
Let’s try a new example to play with
Suppose our rectangles are:
[1,1,2,3]
[2,1,3,2]
[2,2,3,3]
[1,3,3,4]
Let’s draw it in our minds or on paper. What shape is this forming?
Looks like it’s trying to form a big rectangle from (1,1) to (3,4), right?
So, now we:
- Add the area of each.
- Track the smallest x and y → (1,1), and the largest x and y → (3,4), to compute the bounding area.
- Count every corner’s appearance.
If total area of small rectangles is equal to the area of the big rectangle, and only the four corners of the bounding box appear once, and all others appear 2 or 4 times...
Then what can we say?
It must be a perfect rectangle cover!
So what approach are we really using here?
It looks like we are simulating a kind of sweep over the rectangles, counting points as we go—checking coverage and overlaps.
This idea of tracking how geometry overlaps by sweeping across or accumulating frequency is actually similar to what's known as the Line Sweep algorithm.
Also, the way we ensure no double-counting or missing parts using area comparisons and prefix sums of point counts? That's like a prefix sum technique, but in 2D.
So even though we didn’t say it upfront, what we’re doing is combining prefix area checking with a kind of geometric line sweep based on corners.
What needs to be true?
- Total area of small rectangles == Area of bounding rectangle
- Only the corners of the bounding rectangle appear exactly once
- All other points appear exactly 2 or 4 times
If all that is good, we return true. Otherwise, somewhere in there is either a gap or an overlap → false.
Yes! Now, let’s outline the steps of our Algorithm
Perfect Rectangle Algorithm
1. Initialize values:
- totalArea = 0 — to keep track of the sum of all small rectangles' areas.
- Set the boundaries of the outer (bounding) rectangle:
- minX, minY, maxX, maxY initialized from the first rectangle.
- Create a Map<Point, Integer> to count the frequency of all corner points.
2. Process each rectangle:
For each rectangle [x1, y1, x2, y2]:
- Add the rectangle's area to totalArea:
- (x2 - x1) * (y2 - y1)
- Update the bounding box:
- minX = min(minX, x1)
- minY = min(minY, y1)
- maxX = max(maxX, x2)
- maxY = max(maxY, y2)
- For each of the 4 corners:
- Increment its count in the cornerFrequencyMap:
- Bottom-left: (x1, y1)
- Top-left: (x1, y2)
- Top-right: (x2, y2)
- Bottom-right: (x2, y1)
- Increment its count in the cornerFrequencyMap:
3. Validate the outer rectangle:
- Compute the expected area of the bounding rectangle:
- (maxX - minX) * (maxY - minY)
- Return false if:
- totalArea ≠ area of bounding rectangle
- Any of the four bounding box corners do not appear exactly once in the map
4. Remove the four outer corners:
- Delete the following from the cornerFrequencyMap:
- (minX, minY)
- (minX, maxY)
- (maxX, maxY)
- (maxX, minY)
5. Check interior corners:
- All remaining corners in the map must have frequency 2 or 4 (shared between rectangles)
- Use .allMatch(count -> count == 2 || count == 4)
Return: true if all checks pass, otherwise false.
Dry-Run
Input rectangles =[[1,1,2,2],[1,2,2,3],[2,1,3,2],[2,2,3,3]]
Output: true
Step-by-Step Dry Run
Initialize:
- totalArea = 0
- Bounding box:
- minX = 1, minY = 1
- maxX = 2, maxY = 2
- cornerCount = {}
Process Each Rectangle
[1, 1, 2, 2]:
- Area = (2−1)*(2−1) = 1 → totalArea = 1
- Corners:
- (1,1): 1
- (1,2): 1
- (2,2): 1
- (2,1): 1
cornerCount = {
(1,1): 1, (1,2): 1, (2,2): 1, (2,1): 1
}
[1, 2, 2, 3]:
- Area = 1 → totalArea = 2
- Update maxY = 3
- Corners:
- (1,2): +1 → 2
- (1,3): 1
- (2,3): 1
- (2,2): +1 → 2
cornerCount = {
(1,1): 1, (1,2): 2, (1,3): 1,
(2,2): 2, (2,1): 1, (2,3): 1
}
[2, 1, 3, 2]:
- Area = 1 → totalArea = 3
- Update maxX = 3
- Corners:
- (2,1): +1 → 2
- (2,2): +1 → 3
- (3,2): 1
- (3,1): 1
cornerCount = {
(1,1): 1, (1,2): 2, (1,3): 1,
(2,2): 3, (2,1): 2, (2,3): 1,
(3,2): 1, (3,1): 1
}
[2, 2, 3, 3]:
- Area = 1 → totalArea = 4
- Corners:
- (2,2): +1 → 4
- (2,3): +1 → 2
- (3,3): 1
- (3,2): +1 → 2
cornerCount = {
(1,1): 1, (1,2): 2, (1,3): 1,
(2,2): 4, (2,1): 2, (2,3): 2,
(3,2): 2, (3,1): 1, (3,3): 1
}
Bounding Rectangle
- minX = 1, minY = 1
- maxX = 3, maxY = 3
- Expected area = (3−1)*(3−1) = 4
- totalArea = 4, matches bounding rectangle area
Check Corner Appearances:
Bounding Box Corners (should appear exactly once):
- (1,1): 1
- (1,3): 1
- (3,1): 1
- (3,3): 1
Remove these from map.
Remaining corners must appear 2 or 4 times:
Remaining cornerCount:
- (1,2): 2
- (2,2): 4
- (2,1): 2
- (2,3): 2
- (3,2): 2
All values are 2 or 4 → Valid!
Final Result: return true;
Perfect Rectangle Solution
Now lets checkout the "Perfect Rectangle code in C++ , Java, Python and JavaScript.
"Perfect Rectangle" Code in all Languages.
1. Perfect Rectangle solution in C++ Try on Compiler
#include <iostream>
#include <vector>
#include <unordered_map>
#include <set>
#include <utility>
using namespace std;
// Custom hash for pair to use in unordered_map
struct hash_pair {
size_t operator()(const pair<int, int>& p) const {
return hash<long long>()(((long long)p.first) << 32 | (unsigned int)p.second);
}
};
class RectangleCoverChecker {
public:
bool isRectangleCover(vector<vector<int>>& rectangles) {
// Initialize bounding box and area
long long totalArea = 0;
int minX = rectangles[0][0];
int minY = rectangles[0][1];
int maxX = rectangles[0][2];
int maxY = rectangles[0][3];
// Map to count corner appearances
unordered_map<pair<int, int>, int, hash_pair> cornerCount;
// Process each rectangle
for (const auto& rect : rectangles) {
// Calculate and add current rectangle area
totalArea += (long long)(rect[2] - rect[0]) * (rect[3] - rect[1]);
// Update bounding box
minX = min(minX, rect[0]);
minY = min(minY, rect[1]);
maxX = max(maxX, rect[2]);
maxY = max(maxY, rect[3]);
// Count each corner
cornerCount[{rect[0], rect[1]}}]++;
cornerCount[{rect[0], rect[3]}}]++;
cornerCount[{rect[2], rect[3]}}]++;
cornerCount[{rect[2], rect[1]}}]++;
}
// Check bounding rectangle area match
if (totalArea != (long long)(maxX - minX) * (maxY - minY) ||
cornerCount[{minX, minY}] != 1 ||
cornerCount[{minX, maxY}] != 1 ||
cornerCount[{maxX, maxY}] != 1 ||
cornerCount[{maxX, minY}] != 1) {
return false;
}
// Remove the bounding box corners
cornerCount.erase({minX, minY});
cornerCount.erase({minX, maxY});
cornerCount.erase({maxX, maxY});
cornerCount.erase({maxX, minY});
// All other corners must appear 2 or 4 times
for (const auto& [_, count] : cornerCount) {
if (count != 2 && count != 4) return false;
}
return true;
}
};
int main() {
// Read number of rectangles
int n;
cin >> n;
// Read rectangle data
vector<vector<int>> rectangles(n, vector<int>(4));
for (int i = 0; i < n; ++i)
for (int j = 0; j < 4; ++j)
cin >> rectangles[i][j];
// Create instance and invoke method
RectangleCoverChecker checker;
bool result = checker.isRectangleCover(rectangles);
cout << (result ? "true" : "false") << endl;
return 0;
}
2. Perfect Rectangle Solution in Java Try on Compiler
import java.util.*;
public class RectangleCoverChecker {
public boolean isRectangleCover(int[][] rectangles) {
// Initialize total area and bounding rectangle edges
long totalArea = 0;
int minX = rectangles[0][0];
int minY = rectangles[0][1];
int maxX = rectangles[0][2];
int maxY = rectangles[0][3];
// Map to store corner points and their frequency
Map<Point, Integer> cornerCount = new HashMap<>();
// Loop through each rectangle
for (int[] rectangle : rectangles) {
// Add area of current rectangle to total area
totalArea += (long) (rectangle[2] - rectangle[0]) * (rectangle[3] - rectangle[1]);
// Update the bounding box limits
minX = Math.min(minX, rectangle[0]);
minY = Math.min(minY, rectangle[1]);
maxX = Math.max(maxX, rectangle[2]);
maxY = Math.max(maxY, rectangle[3]);
// Track frequency of each corner point
cornerCount.merge(new Point(rectangle[0], rectangle[1]), 1, Integer::sum);
cornerCount.merge(new Point(rectangle[0], rectangle[3]), 1, Integer::sum);
cornerCount.merge(new Point(rectangle[2], rectangle[3]), 1, Integer::sum);
cornerCount.merge(new Point(rectangle[2], rectangle[1]), 1, Integer::sum);
}
// Check if total area equals area of bounding rectangle
if (totalArea != (long) (maxX - minX) * (maxY - minY)
|| cornerCount.getOrDefault(new Point(minX, minY), 0) != 1
|| cornerCount.getOrDefault(new Point(minX, maxY), 0) != 1
|| cornerCount.getOrDefault(new Point(maxX, maxY), 0) != 1
|| cornerCount.getOrDefault(new Point(maxX, minY), 0) != 1) {
return false;
}
// Remove corners of the bounding box
cornerCount.remove(new Point(minX, minY));
cornerCount.remove(new Point(minX, maxY));
cornerCount.remove(new Point(maxX, maxY));
cornerCount.remove(new Point(maxX, minY));
// Remaining corners should appear 2 or 4 times
return cornerCount.values().stream().allMatch(count -> count == 2 || count == 4);
}
// Class representing a Point
private static class Point {
final int x, y;
Point(int x, int y) {
this.x = x;
this.y = y;
}
@Override
public boolean equals(Object o) {
if (this == o) return true;
if (o == null || getClass() != o.getClass()) return false;
Point point = (Point) o;
return x == point.x && y == point.y;
}
@Override
public int hashCode() {
return Objects.hash(x, y);
}
}
// Main method to scan input
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
// Read number of rectangles
int n = scanner.nextInt();
// Read rectangles into 2D array
int[][] rectangles = new int[n][4];
for (int i = 0; i < n; i++) {
for (int j = 0; j < 4; j++) {
rectangles[i][j] = scanner.nextInt();
}
}
// Create instance and invoke method
RectangleCoverChecker checker = new RectangleCoverChecker();
boolean result = checker.isRectangleCover(rectangles);
System.out.println(result);
}
}
3. Perfect Rectangle Solution in Python Try on Compiler
from collections import defaultdict
class RectangleCoverChecker:
def is_rectangle_cover(self, rectangles):
# Initialize bounding box and total area
total_area = 0
min_x, min_y = rectangles[0][0], rectangles[0][1]
max_x, max_y = rectangles[0][2], rectangles[0][3]
# Dictionary to store corner frequencies
corner_count = defaultdict(int)
# Iterate through each rectangle
for x1, y1, x2, y2 in rectangles:
# Add current rectangle area
total_area += (x2 - x1) * (y2 - y1)
# Update bounding box
min_x = min(min_x, x1)
min_y = min(min_y, y1)
max_x = max(max_x, x2)
max_y = max(max_y, y2)
# Count corners
for point in [(x1, y1), (x1, y2), (x2, y2), (x2, y1)]:
corner_count[point] += 1
# Check total area against bounding rectangle area
if total_area != (max_x - min_x) * (max_y - min_y):
return False
# Check that each corner of bounding rectangle appears exactly once
for corner in [(min_x, min_y), (min_x, max_y), (max_x, max_y), (max_x, min_y)]:
if corner_count[corner] != 1:
return False
del corner_count[corner]
# All other corners must appear 2 or 4 times
return all(count in (2, 4) for count in corner_count.values())
if __name__ == "__main__":
# Read number of rectangles
n = int(input())
# Read rectangle input
rectangles = [list(map(int, input().split())) for _ in range(n)]
# Check rectangle cover
checker = RectangleCoverChecker()
print(checker.is_rectangle_cover(rectangles))
4. Perfect Rectangle solution in JavaScript Try on Compiler
const readline = require('readline');
// Function to stringify points
function pointKey(x, y) {
return `${x},${y}`;
}
class RectangleCoverChecker {
isRectangleCover(rectangles) {
// Initialize area and bounding box
let totalArea = 0;
let minX = rectangles[0][0];
let minY = rectangles[0][1];
let maxX = rectangles[0][2];
let maxY = rectangles[0][3];
const cornerMap = new Map();
// Process each rectangle
for (const [x1, y1, x2, y2] of rectangles) {
// Add rectangle area
totalArea += (x2 - x1) * (y2 - y1);
// Update bounding box
minX = Math.min(minX, x1);
minY = Math.min(minY, y1);
maxX = Math.max(maxX, x2);
maxY = Math.max(maxY, y2);
// Track corner counts
for (const [x, y] of [[x1, y1], [x1, y2], [x2, y2], [x2, y1]]) {
const key = pointKey(x, y);
cornerMap.set(key, (cornerMap.get(key) || 0) + 1);
}
}
// Validate total area with bounding rectangle
if (totalArea !== (maxX - minX) * (maxY - minY)) return false;
// Validate 4 unique corners
for (const [x, y] of [[minX, minY], [minX, maxY], [maxX, maxY], [maxX, minY]]) {
const key = pointKey(x, y);
if (cornerMap.get(key) !== 1) return false;
cornerMap.delete(key);
}
// Remaining corners should appear 2 or 4 times
for (const count of cornerMap.values()) {
if (count !== 2 && count !== 4) return false;
}
return true;
}
}
// Read input using readline
const rl = readline.createInterface({
input: process.stdin,
output: process.stdout
});
const inputLines = [];
rl.on('line', line => {
inputLines.push(line.trim());
});
rl.on('close', () => {
// Read number of rectangles
const n = parseInt(inputLines[0]);
// Read rectangles
const rectangles = inputLines.slice(1, n + 1).map(line => line.split(' ').map(Number));
// Run checker
const checker = new RectangleCoverChecker();
const result = checker.isRectangleCover(rectangles);
console.log(result);
});
Perfect Rectangle Complexity Analysis
Time Complexity: O(n)
Bounding box computation and area summation:
for (int[] rectangle : rectangles)
- Happens once for all rectangles → O(n)
- Constant-time operations inside the loop: area calculation, min/max updates, 4 corner updates → O(1) per rectangle
- HashMap insertions (corner frequencies): 4 insertions per rectangle → O(4n) = O(n)
- Final check of 4 bounding box corners → O(1)
- Stream check on cornerCount map values:
At most 4n keys (since each rectangle contributes 4 corners)
But in reality, many corners will overlap, so max unique corners ≤ 4n
→ Worst-case: O(n)
Overall Time Complexity: O(n)
Space Complexity: O(n)
Auxiliary space complexity refers Temporary/extra space used excluding input.
Data structures:
cornerFrequencyMap: Stores frequency for each corner → max 4n keys
→ O(n)
Point objects: Up to 4 new Point objects per rectangle → O(n) in total (since Java's HashMap holds references)
Auxiliary Space: O(n)
Total Space Complexity
Total space includes input + auxiliary.
- Input array rectangles: size n × 4 → O(n)
- cornerFrequencyMap: up to 4n entries → O(n)
- No additional major structures beyond that.
Total Space: O(n)
Similar Problems
You are a professional robber planning to rob houses along a street. Each house has a certain amount of money stashed, the only constraint stopping you from robbing each of them is that adjacent houses have security systems connected and it will automatically contact the police if two adjacent houses were broken into on the same night.
Given an integer array nums representing the amount of money of each house, return the maximum amount of money you can rob tonight without alerting the police.
Consider a rat placed at position (0, 0) in an n x n square matrix mat. The rat's goal is to reach the destination at position (n-1, n-1). The rat can move in four possible directions: 'U'(up), 'D'(down), 'L' (left), 'R' (right).
The matrix contains only two possible values:
- 0: A blocked cell through which the rat cannot travel.
- 1: A free cell that the rat can pass through.