Number of Wonderful Substrings Solution In C++/Java/Python/JS
Problem Description
A wonderful string is a string where at most one letter appears an odd number of times.
For example, "ccjjc" and "abab" are wonderful, but "ab" is not.
Given a string word that consists of the first ten lowercase English letters ('a' through 'j'), return the number of wonderful non-empty substrings in word. If the same substring appears multiple times in word, then count each occurrence separately.

What is a substring?
A substring is a contiguous sequence of characters in a string.
Examples
Input: word = "aba"
Output: 4
Explanation: The four wonderful substrings are underlined below:
- "aba" -> "a"
- "aba" -> "b"
- "aba" -> "a"
- "aba" -> "aba"
Input: word = "aabb"
Output: 9
Explanation: The nine wonderful substrings are underlined below:
- "aabb" -> "a"
- "aabb" -> "aa"
- "aabb" -> "aab"
- "aabb" -> "aabb"
- "aabb" -> "a"
- "aabb" -> "abb"
- "aabb" -> "b"
- "aabb" -> "bb"
- "aabb" -> "b"
Input: word = "he"
Output: 2
Explanation: The two wonderful substrings are underlined below:
- "he" -> "h"
- "he" -> "e"
Constraints
1 <= word.length <= 10^5
word consists of lowercase English letters from 'a' to 'j'.
The very first question that comes to our mind after reading the problem is: How can we efficiently count the number of wonderful substrings in the given word? Most of us already know that one straightforward way is to generate all possible substrings of the word and check whether each satisfies the condition that at most one character appears an odd number of times. To build a solid understanding, let's start by exploring this brute-force approach in detail. This will help us grasp the core concept of what makes a substring "wonderful" and how character frequencies determine it.
Brute Force Approach
Intuition
Since we want to count all substrings in the given word that are wonderful, the first idea that comes to our mind is to generate all possible substrings of the word and check if each one is wonderful or not. For example, if the word has 4 letters, we go through it and take out every possible substring starting from each position and ending at every position after it.
Why Exactly Check Every Substring?
A wonderful string is one where at most one letter appears an odd number of times. So, to find such substrings, we need to look at each one and count how many characters appear an odd number of times. For example, if we take "aba", the letter 'a' appears twice and 'b' appears once. Only one letter ('b') has an odd count, so it’s wonderful. But if we take "ab", both 'a' and 'b' appear once—that means two letters have an odd count, so it’s not wonderful. That’s why we have to check every substring and see if it follows this rule.
To do this, we can use 2 loops. The outer loop will pick the start of the substring, and the inner loop will keep adding 1 character at a time to form longer and longer substrings from that starting point.
Generating All Substrings using Nested Loops
To implement this, we first fix the starting index i of the substring in the word using an outer loop. This loop runs from i = 0 up to i < word.length(), so that we consider every possible starting point of a substring.
For each fixed starting index i, we use an inner loop with index j to build substrings by adding 1 character at a time. This inner loop runs from j = i to j < word.length(). We start with an empty string sub and keep appending word[j] to it. This way, we generate all substrings starting at index i.
This step-by-step method helps beginners clearly understand how substrings are formed by using character positions, instead of directly using built-in substring functions.
Let’s consider an example to see how this works. Suppose word = "aabb". Using the loops:
At i = 0, the inner loop builds:
j = 0 → substring = "a"
j = 1 → substring = "aa"
j = 2 → substring = "aab"
j = 3 → substring = "aabb"
At i = 1, the inner loop builds:
j = 1 → substring = "a"
j = 2 → substring = "ab"
j = 3 → substring = "abb"
At i = 2, the inner loop builds:
j = 2 → substring = "b"
j = 3 → substring = "bb"
At i = 3, the inner loop builds:
j = 3 → substring = "b"
Each substring is built step by step, starting from every index. After generating these substrings, we can then move on to check if they are wonderful or not.
Once we have a substring from word, the next task is to check whether this substring is wonderful or not.
How Do We Know a Substring is Wonderful?
Once we build a substring, the next step is to check if it follows the rule for being wonderful. According to the rule, a substring is wonderful if at most 1 letter appears an odd number of times. This means that all letters must appear an even number of times, or exactly 1 letter can appear an odd number of times—but not more than 1.
To do this, we go through our frequency array (which tracks how many times each letter 'a' to 'j' has appeared in the substring) and count how many letters have an odd count. For example:
If the frequency array is [2, 2, 0, 0, ..., 0], it means 'a' and 'b' both appeared 2 times—so 0 letters have an odd count. This is wonderful.
If the frequency array is [1, 2, 0, 0, ..., 0], it means 'a' appeared 1 time and 'b' appeared 2 times—only 1 letter has an odd count. This is also wonderful.
But if the frequency array is [1, 1, 0, 0, ..., 0], both 'a' and 'b' appeared 1 time—2 letters have an odd count. This is not wonderful.
So, after checking the frequency of all letters in the substring, if the number of odd counts is 0 or 1, we increase our final count.
Then finally we return this final count as the answer.
Approach
Step 1: Initialize a Variable to Store the Result
We start by creating a variable count and initializing it to 0.
This will store the total number of wonderful substrings found in the string.
Step 2: Loop Through the String to Fix the Starting Index i
We use an outer loop that starts from i = 0 and goes up to i < word.length().
This loop picks every possible starting index for a substring.
Step 3: Create the Frequency Array for the Current Starting Point
Before entering the inner loop, we create a frequency array of size 10 (for characters 'a' to 'j') and initialize all values to 0.
This array will keep track of how many times each character has appeared in the current substring.
Step 4: Use an Inner Loop to Expand the Substring Character by Character
We now run an inner loop from j = i to j < word.length().
This loop helps us build every possible substring that starts at index i.
Step 5: Update the Frequency Array for the Current Character
Each time we add a new character word[j] to the substring, we increase its frequency in the array.
This is done using: freq[word[j] - 'a']++
Step 6: Initialize a Variable to Count How Many Letters Have Odd Frequency
We create a variable oddCount and set it to 0.
This will be used to count how many letters in the current substring appear an odd number of times.
Step 7: Run a Loop to Count Odd Frequencies
Now we loop through the frequency array using variable k from 0 to 9 to count odd frequencies ( 0 to 9 because the letters in word can only be form 'a' (0) to 'i' (9).
For each k, we check if freq[k] % 2 != 0.
If true, we increase oddCount by 1.
Step 8: If the Substring is Wonderful, Increase the Count
If oddCount is 0 or 1, it means the substring meets the condition of being wonderful.
In that case, we increase the count by 1.
Step 9: After All Loops, Return the Final Count
Once both outer and inner loops are complete, we return the value stored in count.
This gives us the total number of wonderful substrings in the input string.
This number represents the total number of wonderful substrings in the input string.
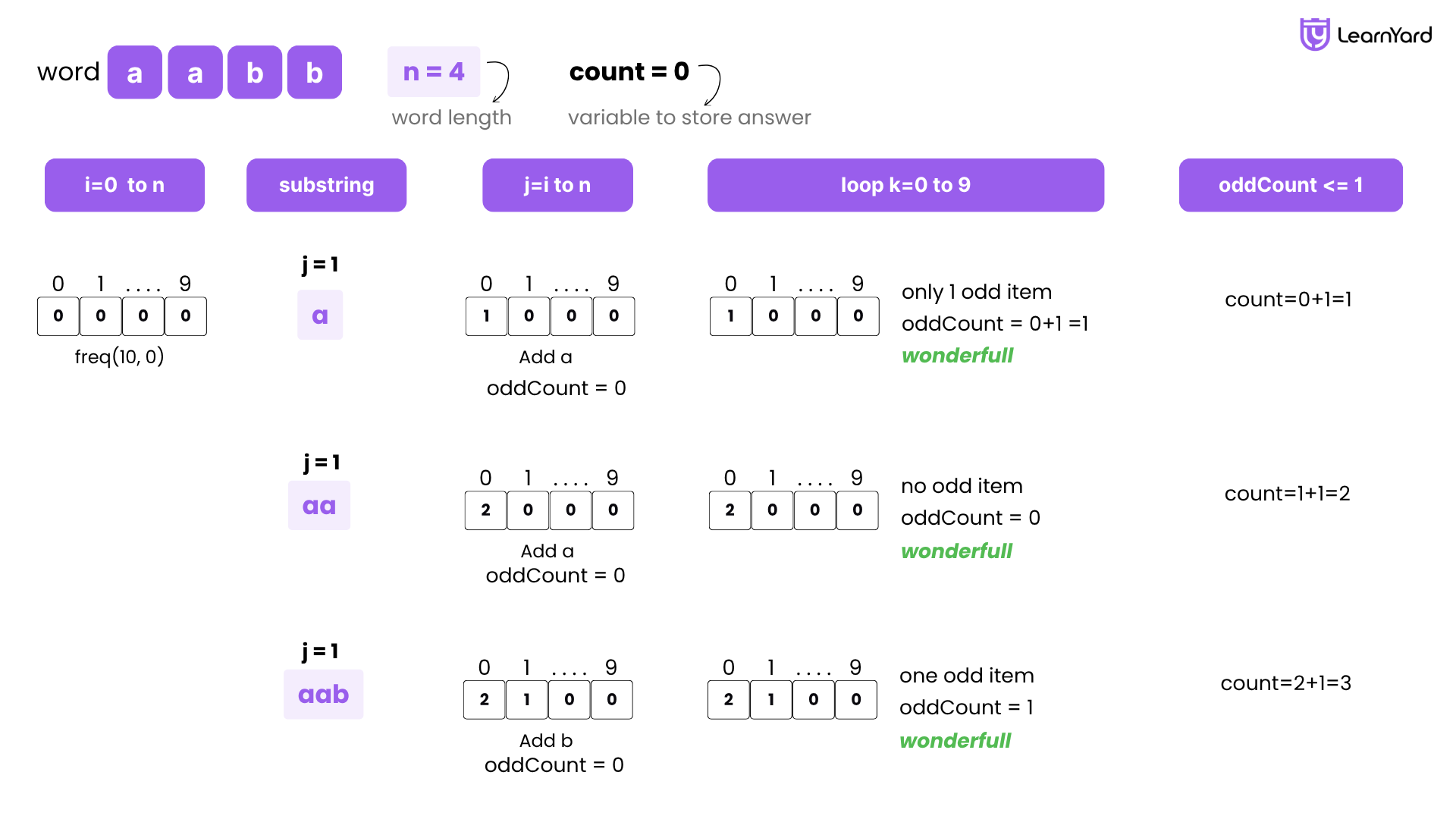
Dry Run
Let’s do a detailed dry run of the brute-force approach using nested loops and frequency checking for the input:
word = "aabb"
We want to find all substrings where at most one letter appears an odd number of times.
Step 1: Initialize a Variable to Store the Result
We start by initializing count = 0. This will hold the total number of wonderful substrings.
Step 2: Loop Through the String to Fix the Starting Index i
We begin with i = 0 and go up to i = word.length() - 1 (i.e., i = 3).
Step 3: Create the Frequency Array for the Current Starting Point
For each value of i, we create a fresh array freq[10] initialized with all 0s. This will track the frequency of characters from 'a' to 'j'.
Step 4: Use an Inner Loop to Expand the Substring Character by Character
We run an inner loop from j = i to j = word.length() - 1. At each step, we add word[j] to the current substring and update the frequency array.
Iteration-Wise Dry Run
i = 0 → Starting from character 'a'
freq = [0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
- j = 0 → Substring: "a"
Step 5: Add 'a' → freq[0] = 1
Step 6: Set oddCount = 0
Step 7: Loop k = 0 to 9Step 8: Since oddCount = 1, this is a wonderful substring → increment count = 1 - k = 0: freq[0] = 1 → odd → increment oddCount = 1
- k = 1 to 9: freq[k] = 0 → even → no change
- j = 1 → Substring: "aa"
Step 5: Add 'a' → freq[0] = 2
Step 6: Set oddCount = 0
Step 7: - k = 0 to 9: all even
Step 8: oddCount = 0 → wonderful → count = 2
- k = 0 to 9: all even
- j = 2 → Substring: "aab"
Step 5: Add 'b' → freq[1] = 1
Step 6: Set oddCount = 0
Step 7: - k = 0: freq[0] = 2 → even
- k = 1: freq[1] = 1 → odd → oddCount = 1
- k = 2 to 9: even
Step 8: oddCount = 1 → wonderful → count = 3
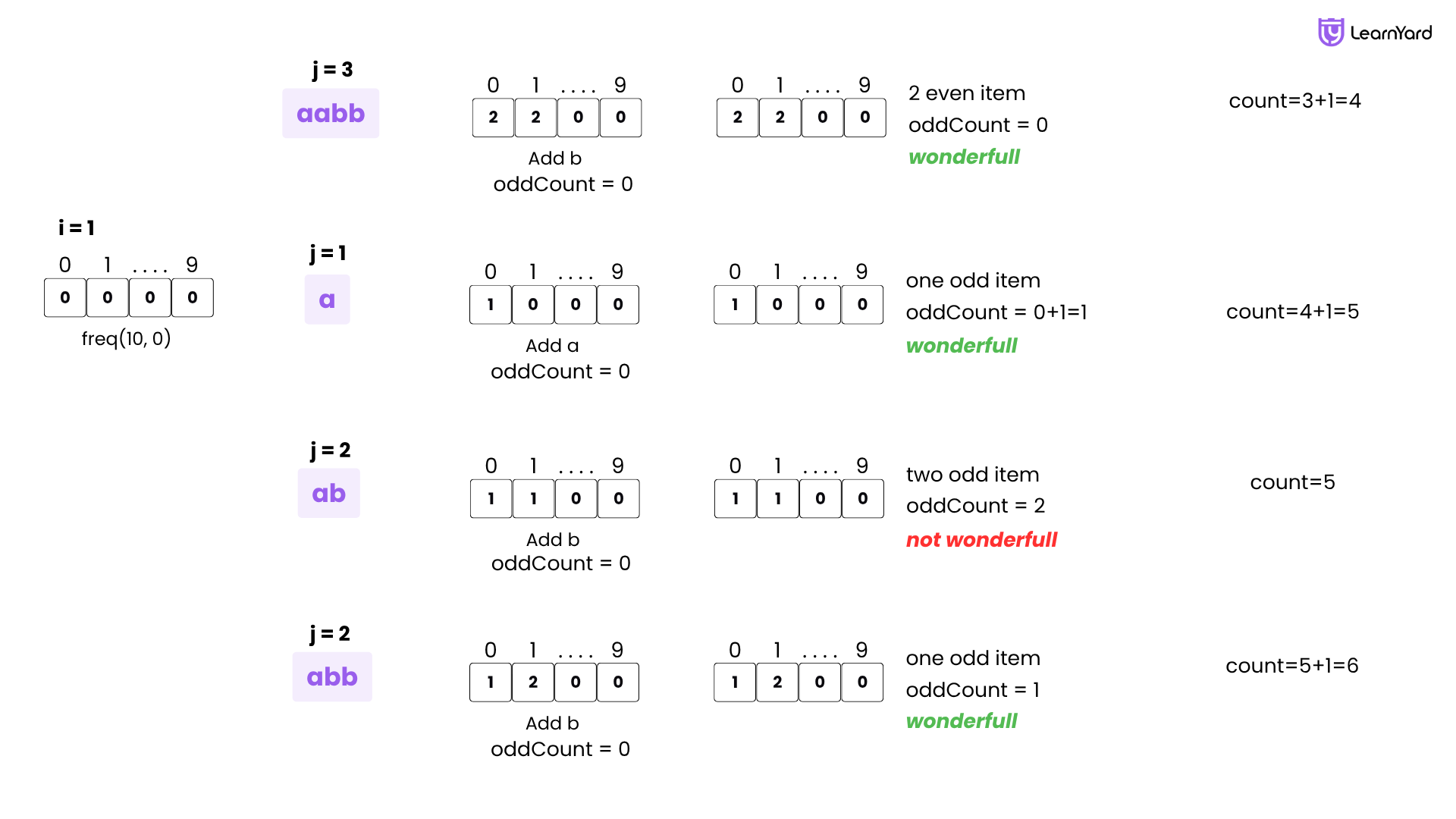
- j = 3 → Substring: "aabb"
Step 5: Add 'b' → freq[1] = 2
Step 6: Set oddCount = 0
Step 7: - k = 0, 1: even
- k = 2 to 9: even
Step 8: oddCount = 0 → wonderful → count = 4
i = 1 → Starting from second 'a'
freq = [0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
- j = 1 → Substring: "a"
Add 'a' → freq[0] = 1
Set oddCount = 0 - k = 0: odd → oddCount = 1
Step 8: oddCount = 1 → valid → count = 5
- k = 0: odd → oddCount = 1
- j = 2 → Substring: "ab"
Add 'b' → freq[1] = 1
Set oddCount = 0 - k = 0: odd → oddCount = 1
- k = 1: odd → oddCount = 2
Step 8: oddCount = 2 → not valid → count = 5
- j = 3 → Substring: "abb"
Add 'b' → freq[1] = 2
Set oddCount = 0 - k = 0: odd → oddCount = 1
- k = 1: even
Step 8: oddCount = 1 → valid → count = 6
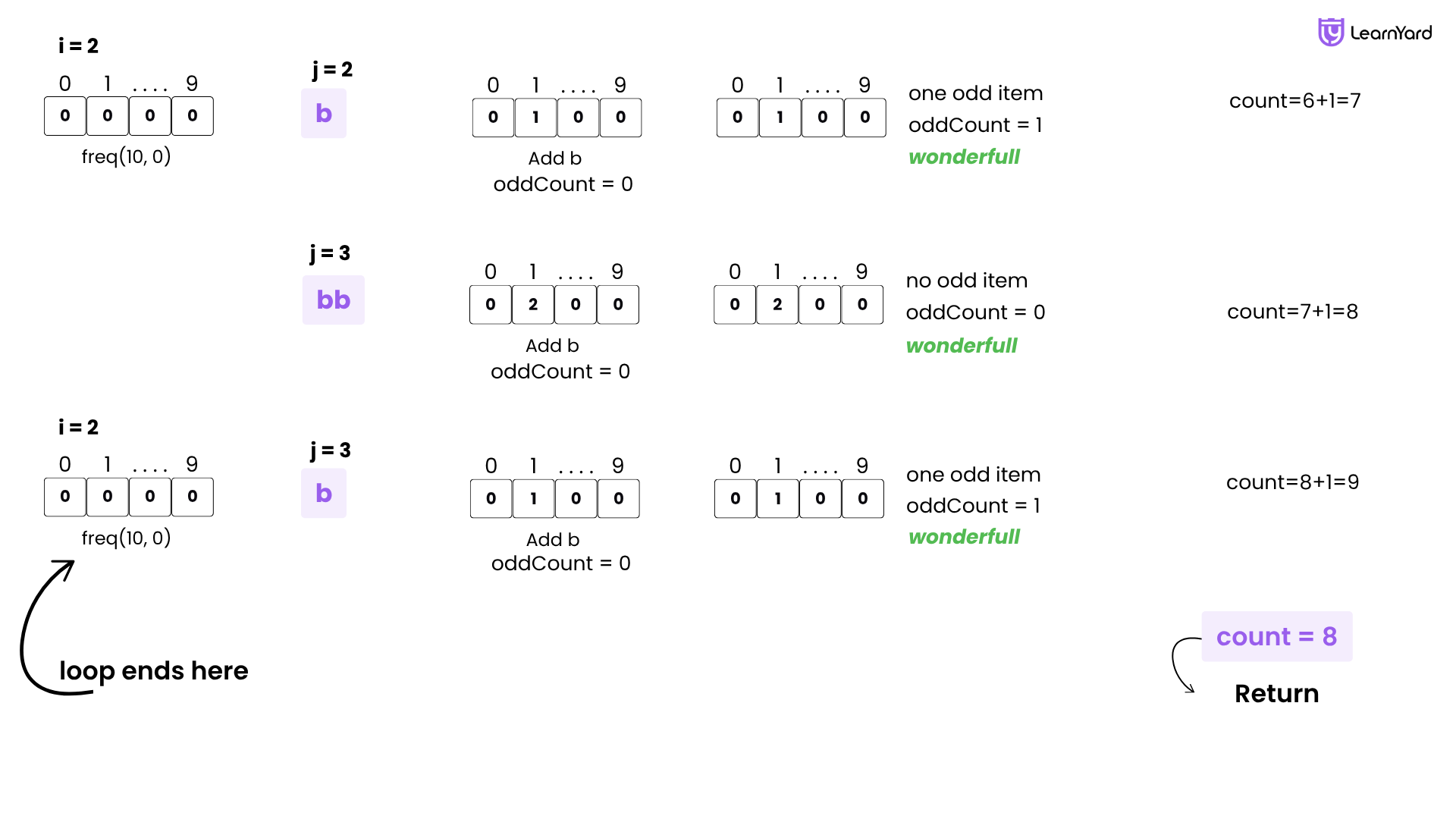
i = 2 → Starting from first 'b'
freq = [0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
- j = 2 → Substring: "b"
Add 'b' → freq[1] = 1
Set oddCount = 0 - k = 1: odd → oddCount = 1
Step 8: valid → count = 7
- k = 1: odd → oddCount = 1
- j = 3 → Substring: "bb"
Add 'b' → freq[1] = 2
Set oddCount = 0 - k = 1: even → no change
Step 8: valid → count = 8
- k = 1: even → no change
i = 3 → Starting from second 'b'
freq = [0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
- j = 3 → Substring: "b"
Add 'b' → freq[1] = 1
Set oddCount = 0 - k = 1: odd → oddCount = 1
Step 8: valid → count = 9
- k = 1: odd → oddCount = 1
Final Result
The total number of wonderful substrings in "aabb" is: count =9
These substrings are:
- "a" (from i = 0)
- "aa"
- "aab"
- "aabb"
- "a" (from i = 1)
- "abb"
- "b" (from i = 2)
- "bb"
- "b" (from i = 3)
Code for All Languages
C++
#include <iostream> // For input and output
#include <vector> // For using the vector data structure
#include <string> // For handling strings
using namespace std;
class Solution {
public:
long long wonderfulSubstrings(string word) {
// Step 1: Initialize a variable to store the result
long long count = 0;
int n = word.length();
// Step 2: Loop through the string to fix the starting index i
for (int i = 0; i < n; i++) {
// Step 3: Create the frequency array for the current starting point
vector<int> freq(10, 0); // For letters 'a' to 'j'
// Step 4: Use an inner loop to expand the substring character by character
for (int j = i; j < n; j++) {
// Step 5: Update the frequency for the current character
freq[word[j] - 'a']++;
// Step 6: Initialize a variable to count how many letters have an odd frequency
int oddCount = 0;
// Step 7: Loop k = 0 to 9 to count odd frequencies
for (int k = 0; k < 10; k++) {
if (freq[k] % 2 == 1) {
oddCount++;
}
}
// Step 8: If the substring is wonderful, increment the result count
if (oddCount <= 1) {
count++;
}
}
}
// Step 9: After all loops, return the result
return count;
}
};
int main() {
string word;
cin >> word;
Solution sol;
long long result = sol.wonderfulSubstrings(word); // Call the function
// Output the result
cout << result << endl;
return 0;
}
Java
import java.util.*; // For Scanner and Arrays
class Solution {
public long wonderfulSubstrings(String word) {
// Step 1: Initialize a variable to store the result
long count = 0;
int n = word.length();
// Step 2: Loop through the string to fix the starting index i
for (int i = 0; i < n; i++) {
// Step 3: Create the frequency array for the current starting point
int[] freq = new int[10]; // For letters 'a' to 'j'
// Step 4: Use an inner loop to expand the substring character by character
for (int j = i; j < n; j++) {
// Step 5: Update the frequency for the current character
freq[word.charAt(j) - 'a']++;
// Step 6: Initialize a variable to count how many letters have an odd frequency
int oddCount = 0;
// Step 7: Loop k = 0 to 9 to count odd frequencies
for (int k = 0; k < 10; k++) {
if (freq[k] % 2 == 1) {
oddCount++;
}
}
// Step 8: If the substring is wonderful, increment the result count
if (oddCount <= 1) {
count++;
}
}
}
// Step 9: After all loops, return the result
return count;
}
}
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
// Input the string (no prompt, as per format)
String word = sc.next();
Solution sol = new Solution();
long result = sol.wonderfulSubstrings(word); // Call the function
// Output the result
System.out.println(result);
}
}
Python
class Solution:
def wonderfulSubstrings(self, word: str) -> int:
# Step 1: Initialize a variable to store the result
count = 0
n = len(word)
# Step 2: Loop through the string to fix the starting index i
for i in range(n):
# Step 3: Create the frequency array for the current starting point
freq = [0] * 10 # For letters 'a' to 'j'
# Step 4: Use an inner loop to expand the substring character by character
for j in range(i, n):
# Step 5: Update the frequency for the current character
freq[ord(word[j]) - ord('a')] += 1
# Step 6: Initialize a variable to count how many letters have an odd frequency
oddCount = 0
# Step 7: Loop k = 0 to 9 to count odd frequencies
for k in range(10):
if freq[k] % 2 == 1:
oddCount += 1
# Step 8: If the substring is wonderful, increment the result count
if oddCount <= 1:
count += 1
# Step 9: After all loops, return the result
return count
# Driver Code
if __name__ == "__main__":
word = input() # Input the string
sol = Solution()
result = sol.wonderfulSubstrings(word) # Call the function
# Output the result
print(result)
Javascript
/**
* @param {string} word - The input string consisting of letters from 'a' to 'j'
* @return {number} - Total number of wonderful substrings
*/
var wonderfulSubstrings = function(word) {
// Step 1: Initialize a variable to store the result
let count = 0;
const n = word.length;
// Step 2: Loop through the string to fix the starting index i
for (let i = 0; i < n; i++) {
// Step 3: Create the frequency array for the current starting point
let freq = new Array(10).fill(0); // For letters 'a' to 'j'
// Step 4: Use an inner loop to expand the substring character by character
for (let j = i; j < n; j++) {
// Step 5: Update the frequency for the current character
freq[word.charCodeAt(j) - 'a'.charCodeAt(0)]++;
// Step 6: Initialize a variable to count how many letters have an odd frequency
let oddCount = 0;
// Step 7: Loop k = 0 to 9 to count odd frequencies
for (let k = 0; k < 10; k++) {
if (freq[k] % 2 === 1) {
oddCount++;
}
}
// Step 8: If the substring is wonderful, increment the result count
if (oddCount <= 1) {
count++;
}
}
}
// Step 9: After all loops, return the result
return count;
};
// Driver code
const readline = require("readline");
const rl = readline.createInterface({
input: process.stdin,
output: process.stdout
});
let inputs = [];
rl.on("line", function(line) {
inputs.push(line.trim());
if (inputs.length === 1) {
const word = inputs[0];
const result = wonderfulSubstrings(word);
console.log(result);
rl.close();
}
});
Time Complexity: O(n²)
Outer Loop: O(n)
The outer loop runs from index i = 0 to i = word.length() - 1.
Let’s denote:
n = length of the string word = word.length
So, the outer loop executes approximately n times in the worst case.
Inner Loop: O(n)
For each iteration of the outer loop (for each starting index i), we use an inner loop from j = i to j < n.
This loop generates all substrings that start at index i.
Over all values of i, this results in:
n + (n - 1) + (n - 2) + ... + 1 iterations.
This is an arithmetic series that sums up to:
n(n + 1)/2, which simplifies to O(n²).
Frequency Update: O(1)
Inside the inner loop, we increment the count of the current character in the frequency array.
This operation takes constant time because we are only updating a fixed-size array of 10 elements.
Counting Odd Frequencies: O(10)
After updating the frequency array, we count how many characters have an odd frequency.
We do this by looping through all 10 entries in the frequency array (for 'a' to 'j').
Since this loop runs a fixed number of times, it also takes constant time — O(10), which is O(1).
Total Time per Substring: O(1)
Each substring is processed in constant time — frequency update and checking for odd counts both take O(1) time.
Final Time Complexity: O(n²)
We perform O(1) work for each of the O(n²) substrings formed by the nested loops.
So, the total time complexity is: O(n²)
Space Complexity: O(1)
Auxiliary Space Complexity: O(1)
This refers to any extra space used by the algorithm that is independent of the input and output space.
In our brute-force approach, we use:
- A frequency array of size 10 to track letter counts from 'a' to 'j'
- A few integer variables like count, oddCount, and loop indices
The frequency array is fixed in size and does not depend on the length of the input string.
No additional data structures grow with input size.
Therefore, the auxiliary space used in one iteration is constant.
Hence, the auxiliary space complexity is O(1).
Total Space Complexity: O(n)
This includes the space required for:
- Input space: The input string word is of length n, so the input space is O(n).
- Output space: We store only a single integer result, not a list of substrings, so output space is O(1).
- Extra space used by the algorithm: As analyzed above, O(1).
Combining all the space requirements:
Total Space Complexity = O(n) + O(1) + O(1) = O(n).
Will brute force work against the given constraints?
For the current solution, the time complexity is O(n²), which is not suitable for n ≤ 10⁵. This means that for each test case, where the length of the string word is at most 10⁵, the solution might not execute within the given time limits.
Since O(n²) results in a maximum of 10¹⁰ operations (for n = 10⁵), the solution is not expected to work well for larger test cases. In most competitive programming environments, problems can handle up to 10⁶ operations per test case, meaning that for n ≤ 10⁵, the solution with 10¹⁰ operations is not efficient enough.
When multiple test cases are involved, the total number of operations could easily exceed this limit and approach 10¹⁰ operations, especially when there are many test cases or the value of n increases.
Thus, while the solution meets the time limits for a single test case, the O(n²) time complexity poses a risk for Time Limit Exceeded (TLE) errors when handling larger input sizes or multiple test cases. This can be a challenge for competitive programming problems with larger inputs or numerous test cases.
The brute-force method checks every substring’s character frequencies but is too slow. Instead, we can track frequency patterns using bitmasking to avoid redundant work. This lets us count valid substrings much faster.
Let’s see how.
Optimal Approach
Intuition
Let’s pause and reflect on what it means for a substring to be wonderful. A wonderful substring is one where at most one letter appears an odd number of times. For example, substrings like "aa", "aba", or "civic" qualify because either all characters occur an even number of times or just one character occurs an odd number of times. Now think carefully — we don’t need to know the exact counts of each letter; we only need to know whether each letter appears an even or odd number of times.
Instead of tracking actual frequencies, what if we just track whether each character count is odd or even?
If a character count flips from even to odd or from odd to even, we just flip a bit!
So we can represent the state of the frequency of all letters ('a' to 'j') using a bitmask with just 10 bits — one for each letter.
What is a Bitmask?
A bitmask is a clever way to keep track of certain states (like even or odd frequency) using the bits of a single number. In the context of this problem, we use a bitmask to represent whether each of the first 10 lowercase English letters 'a' to 'j' has occurred an even or odd number of times so far.
Rather than storing actual counts for each character, we only need to know:
Has this character appeared an odd number of times?
- If yes, we set its bit to 1.
- If no (even count), we set it to 0.
We store this information using a 10-bit binary number, where each bit corresponds to a letter.
We use one bit per character, where
- A 0 in that bit means the letter has appeared an even number of times (including 0 times),
- A 1 means it has appeared an odd number of times.
So a bitmask like 0000000001 means only 'a' has an odd count so far.
A bitmask like 0000000010 means only 'b' has an odd count so far.
And 0000000000 means all characters have even counts.
As we process the string character by character, we flip the bit corresponding to the character. If a character has occurred an even number of times, it stays 0. If it becomes odd, it flips to 1. This bitmask gives us a compact summary of the frequency parity for the entire prefix of the string.
How Do We Flip a Bit at a Particular Position in a Bitmask?
To flip a bit at position k in a bitmask, we use the following formula:
bitmask = bitmask ^ (1 << k)
Let’s break this down:
- 1 << k creates a number where only the k-th bit is set to 1
- The XOR ( ^ ) operator flips the k-th bit:
- If it was 0, it becomes 1
- If it was 1, it becomes 0
Example: Flipping the bit at position 3
Suppose the current bitmask is 00011010
(Each bit from right to left represents letters 'a' to 'j', with bit 0 for 'a', bit 1 for 'b', ..., bit 9 for 'j')
Now we want to flip the bit at position 3 (for character 'd')
- Compute the mask:
1 << 3 = 00001000 - Apply XOR to flip the bit:
bitmask ^ (1 << 3) = 00011010 ^ 00001000 = 00010010
So after flipping, the new bitmask is 00010010
Why this works
The XOR operator follows these simple rules:
- 1 ^ 1 = 0 → bit turns off
- 0 ^ 1 = 1 → bit turns on
- x ^ 0 = x → bit remains unchanged
This lets us toggle exactly one bit in the bitmask, which is exactly what we want when tracking whether a character’s frequency is currently odd or even.
At this point, we might think — let’s generate all substrings, compute the bitmask for each one, and check how many characters have odd frequency. That would work, but we’d be checking O(n²) substrings. For n up to 10⁵, this leads to O(n²) time, which is not efficient enough.
So how do we optimize this?
Let’s pause and think again: for any substring s[i...j] to be wonderful, the parity (odd/even status) of characters from index i to j must form a bitmask where at most one bit is set. This condition is simple to check.
How to Check if At Most One Bit is Set in a Bitmask?
This is a very common technique in bit manipulation problems — checking whether a binary number has at most one bit set.
Let’s understand what this means.
Suppose we have a number represented in binary. Having “at most one bit set” means that either:
- All bits are 0 (i.e., the number is 0), or
- Exactly one bit is 1 and all others are 0.
Examples:
- 0000000000 → valid (no bits set)
- 0000000100 → valid (only one bit set at position 2)
- 0001000000 → valid (only one bit set at position 6)
- 0001100000 → not valid (two bits set)
Now the question is — how do we check this condition in constant time?Here’s the trick:
Let’s say the bitmask is stored in a variable mask.
We can use this classic condition:
A number has at most one bit set if and only if
mask & (mask - 1) == 0
Why does this work?
Let’s break it down:
- If mask has only one bit set, then subtracting 1 from it will flip that bit to 0 and set all lower bits to 1.
- When we perform mask & (mask - 1), it will always result in 0 in such a case, because there will be no common set bits between mask and mask - 1.
Examples:
- mask = 8 → binary: 00001000
mask - 1 = 7 → binary: 00000111
mask & (mask - 1) = 00000000
since, no bit is set in this value, thus 8 is a valid number. - mask = 12 → binary: 00001100
mask - 1 = 11 → binary: 00001011
mask & (mask - 1) = 00001000
since, a bit is set in this value, thus 12 is not a valid number.
Whenever we want to verify if a bitmask represents a wonderful substring, we just check:
- mask == 0 → all character counts are even → wonderful
- mask & (mask - 1) == 0 → only one character has an odd count → still wonderful
But how do we quickly find how many such substrings exist?
Here’s the clever insight: instead of checking every substring, we track the bitmask for every prefix of the string.
If two prefixes have the same bitmask, it means the substring between them has all even counts — which is wonderful.
How can we say this?
Let’s pause and think: what does it mean for two prefixes to have the same bitmask?
A bitmask at index i tells us the odd/even parity of all characters from the beginning of the string up to index i.
For example, say the bitmask at index i is mask1, and at index j (where j > i) it is also mask1.
That means:
The total count of every character from index 0 to i has the same parity as from index 0 to j.
So, when we subtract the prefix up to i from the prefix up to j, we cancel out the characters that appeared in both parts.
The result is: the substring from i + 1 to j must have even counts for all characters.
Why? Because any difference in count would have shown up as a different bit between the two bitmasks.
So if two prefixes have exactly the same bitmask, the substring between them contains characters with all even counts — and that's one of the valid forms of a wonderful substring.
Similarly we can argue that, if two prefixes differ by exactly one bit, that means the substring between them has only one character with an odd count , implying it is still wonderful.
Explanation:
Suppose the bitmask at index i is mask1, and the bitmask at index j (j > i) is mask2, and they differ by exactly one bit.
This means:
There is exactly one character whose parity (odd/even count) is different between the two prefixes.
All other characters still have the same parity.
So when we subtract the prefix at i from the prefix at j, we get a substring where:
- That one character appears an odd number of times,
- All other characters appear an even number of times.
That is still valid under the definition of a wonderful substring — since we allow at most one character to have an odd count.
So we keep track of how many times each bitmask has occurred as we go through the string. At each step, we can check how many previous prefixes could form a wonderful substring ending at the current character. We just need to find how many past bitmasks are either equal to the current one, or differ from it by exactly one bit.
And how do we track how many times each mask has occurred?
That’s where we use a data structure to store the count of each bitmask seen so far. Since there are only 10 characters, there are only 2¹⁰ = 1024 possible bitmasks. So we can simply use an array of size 1024 to store the counts. It behaves like a hash table, but since the range is small and known in advance, an array is more efficient.
What is Hash Table?
A hashtable is a data structure that stores key-value pairs, using a hash function to compute an index for quick access. It offers average O(1) time complexity for operations like insertion, deletion, and lookup.
But before we start processing our string, we initialize the frequency of bitmask 0 to 1. Lets take a moment to understand why?
Think about what bitmask 0 means — it represents a state where all character frequencies are even (or more precisely, zero at the beginning).
Now, imagine we find a prefix of the string (from the beginning up to some index j) where all character counts happen to be even — in other words, the bitmask at position j is also 0.
This would mean the entire substring from the start (index 0) to index j is already a wonderful substring.
But for us to count this correctly, we must have already recorded that we’ve seen bitmask 0 once — even if it was just the empty prefix before the string began.
By initializing prefixCount[0] = 1, we’re essentially saying:
“Yes, before the string starts, we have a bitmask of all zeros — a clean slate — and we’ve seen that state once.”
This setup ensures that any wonderful substring starting at index 0 is properly counted.
Without this, we’d miss those edge cases where a substring from the beginning of the string forms a valid wonderful substring.
So we can store the occurrences of the bitmask formed from the starting to any index i in our frequency array. For each index i, we would find the number of wonderful substrings ending at index i by checking how many times the same bitmask as of now or a bitmask where just a single bit differs from the current bitmask has been recorded to get the count of valid starting indices of the wonderful substrings that end at index i.
We would keep on accumulating the number of wonderful substrings ending at each index i some variable, and finally return that variable as the required answer.
Why is This Efficient?
Instead of checking every possible substring manually (which would take O(n²) time), we:
- Traverse the string once from left to right, updating a running bitmask that tracks the odd/even parity of character frequencies.
- At each step, we check how many times we’ve seen the current bitmask before using a frequency table (array of size 1024).
- We also check for all 10 possible masks that differ by one bit (to allow for one character to be odd), which takes only 10 operations per character.
- Since both these steps — checking the current bitmask and its 10 neighbors — are done in constant time, each character takes O(1) work.
That gives us an overall linear time solution, which is perfect for large inputs.
We transformed a brute-force substring scanning problem into a prefix parity tracking problem using bitmasks and counting, and that’s what makes this solution both powerful and optimal.
Approach
Step 1: Initialize Variables
We start by initializing the basic variables we’ll need:
- n stores the length of the input string word.
- ans is initialized to 0 and will store our final answer — the count of wonderful substrings.
- bitmask is initialized to 0. This bitmask will help us track the parity (even or odd count) of characters from 'a' to 'j'.
Step 2: Create Prefix Count Map and Initialize
We create a prefixCount array of size 1024, since there are 2¹⁰ = 1024 possible bitmask states for 10 characters.
Each index of this array represents a particular combination of character parities.
We initialize prefixCount[0] = 1 to account for the empty prefix.
This is crucial for counting substrings that are wonderful from the beginning of the string (i.e., prefix itself is wonderful).
Step 3: Traverse the String Character by Character
Now we iterate over each character at index idx from 0 to n in the string word, from left to right.
At each step, we’ll update our current bitmask to reflect the parity of characters we’ve seen so far.
Step 4: Update the Bitmask by Flipping the Current Character’s Bit
We compute the position pos = ch - 'a' (0 for 'a', 1 for 'b', ..., 9 for 'j').
Then we flip the bit at that position in the bitmask using this formula:
bitmask = bitmask ^ (1 << pos)
This toggles the parity of the current character — if it was even before, it becomes odd, and vice versa.
Step 5: Add Substrings Ending Here That Have All Even Counts
If we’ve seen this bitmask before, then it means the substring between the previous occurrence and the current position has all characters with even frequencies.
So we add prefixCount[bitmask] to ans.
Step 6: Loop from 0 to 9 to Check Bitmasks That Differ by Exactly One Bit
Now we check for all bitmasks that differ from the current one by exactly one bit — that is, substrings where exactly one character has an odd count.
Step 7: Add Substrings That Differ by Exactly One Bit
For each i from 0 to 9, we flip the i-th bit in the current bitmask using bitmask ^ (1 << i) and check how many times we’ve seen this new bitmask before.
If we've seen it, it means the substring between that previous occurrence and now has exactly one character with an odd count (rest are even) — which is still a wonderful substring.
We add the count of such bitmasks to ans.
Step 8: Update the Count of the Current Bitmask
Finally, we record the current bitmask in our prefixCount map:
prefixCount[bitmask]++
This is important because future substrings might end here and refer back to this prefix.
Step 9: Return the Final Result
After processing all characters, we return the total count stored in ans.
This gives the number of wonderful substrings in the string word.
Dry Run
Let’s do a step-by-step dry run of the optimized bitmask + prefix-counting approach for word = "aabb"
Step 1: Initialize all required variables
n = 4 (length of input string)
ans = 0 (final count of wonderful substrings)
bitmask = 0 (tracks odd/even status of character frequencies)
Step 2: Create the prefix count array and initialize base case
Create prefixCount[1024] → all values initialized to 0
Set prefixCount[0] = 1
This means: we’ve seen the bitmask 0 (all characters even) once before starting
Step 3: Traverse the string character by character
Index = 0 → character = 'a'
pos = ch - 'a' = 0
1 << pos = 1 << 0 = 1
Update bitmask: bitmask = bitmask ^ (1 << pos) = 0 ^ 1 = 1
Current bitmask: 1
Step 5: Add substrings ending here with all even counts
prefixCount[1] = 0 → no change to ans
Step 6–7: Check bitmasks that differ by exactly one bit from 1
Loop i = 0 to 9:
i = 0 → flipped = 1 ^ (1 << 0) = 1 ^ 1 = 0 → prefixCount[0] = 1 → ans += 1 → ans = 1
i = 1 → flipped = 1 ^ (1 << 1) = 1 ^ 2 = 3 → prefixCount[3] = 0 → no change
i = 2 → flipped = 1 ^ 4 = 5 → prefixCount[5] = 0 → no change
i = 3 → flipped = 1 ^ 8 = 9 → prefixCount[9] = 0 → no change
i = 4 → flipped = 1 ^ 16 = 17 → prefixCount[17] = 0 → no change
i = 5 → flipped = 1 ^ 32 = 33 → prefixCount[33] = 0 → no change
i = 6 → flipped = 1 ^ 64 = 65 → prefixCount[65] = 0 → no change
i = 7 → flipped = 1 ^ 128 = 129 → prefixCount[129] = 0 → no change
i = 8 → flipped = 1 ^ 256 = 257 → prefixCount[257] = 0 → no change
i = 9 → flipped = 1 ^ 512 = 513 → prefixCount[513] = 0 → no change
Step 8: Update prefix count
prefixCount[1] += 1 → prefixCount[1] = 1
Index = 1 → character = 'a'
pos = ch - 'a' = 0
1 << pos = 1
Update bitmask: bitmask = bitmask ^ 1 = 1 ^ 1 = 0
Current bitmask: 0
Step 5: Add substrings ending here with all even counts
prefixCount[0] = 1 → ans += 1 → ans = 2
Step 6–7: Check bitmasks that differ by exactly one bit from 0
Loop i = 0 to 9:
i = 0 → flipped = 0 ^ 1 = 1 → prefixCount[1] = 1 → ans += 1 → ans = 3
i = 1 → flipped = 0 ^ 2 = 2 → prefixCount[2] = 0 → no change
i = 2 → flipped = 0 ^ 4 = 4 → prefixCount[4] = 0 → no change
i = 3 → flipped = 0 ^ 8 = 8 → prefixCount[8] = 0 → no change
i = 4 → flipped = 0 ^ 16 = 16 → prefixCount[16] = 0 → no change
i = 5 → flipped = 0 ^ 32 = 32 → prefixCount[32] = 0 → no change
i = 6 → flipped = 0 ^ 64 = 64 → prefixCount[64] = 0 → no change
i = 7 → flipped = 0 ^ 128 = 128 → prefixCount[128] = 0 → no change
i = 8 → flipped = 0 ^ 256 = 256 → prefixCount[256] = 0 → no change
i = 9 → flipped = 0 ^ 512 = 512 → prefixCount[512] = 0 → no change
Step 8: Update prefix count
prefixCount[0] += 1 → prefixCount[0] = 2
Index = 2 → character = 'b'
pos = ch - 'a' = 1
1 << pos = 2
Update bitmask: bitmask = bitmask ^ 2 = 0 ^ 2 = 2
Current bitmask: 2
Step 5: Add substrings ending here with all even counts
prefixCount[2] = 0 → no change
Step 6–7: Check bitmasks that differ by exactly one bit from 2
Loop i = 0 to 9:
i = 0 → flipped = 2 ^ 1 = 3 → prefixCount[3] = 0 → no change
i = 1 → flipped = 2 ^ 2 = 0 → prefixCount[0] = 2 → ans += 2 → ans = 5
i = 2 → flipped = 2 ^ 4 = 6 → prefixCount[6] = 0 → no change
i = 3 → flipped = 2 ^ 8 = 10 → prefixCount[10] = 0 → no change
i = 4 → flipped = 2 ^ 16 = 18 → prefixCount[18] = 0 → no change
i = 5 → flipped = 2 ^ 32 = 34 → prefixCount[34] = 0 → no change
i = 6 → flipped = 2 ^ 64 = 66 → prefixCount[66] = 0 → no change
i = 7 → flipped = 2 ^ 128 = 130 → prefixCount[130] = 0 → no change
i = 8 → flipped = 2 ^ 256 = 258 → prefixCount[258] = 0 → no change
i = 9 → flipped = 2 ^ 512 = 514 → prefixCount[514] = 0 → no change
Step 8: Update prefix count
prefixCount[2] += 1 → prefixCount[2] = 1
Index = 3 → character = 'b'
pos = ch - 'a' = 1
1 << pos = 2
Update bitmask: bitmask = bitmask ^ 2 = 2 ^ 2 = 0
Current bitmask: 0
Step 5: Add substrings ending here with all even counts
prefixCount[0] = 2 → ans += 2 → ans = 7
Step 6–7: Check bitmasks that differ by exactly one bit from 0
Loop i = 0 to 9:
i = 0 → flipped = 0 ^ 1 = 1 → prefixCount[1] = 1 → ans += 1 → ans = 8
i = 1 → flipped = 0 ^ 2 = 2 → prefixCount[2] = 1 → ans += 1 → ans = 9
i = 2 → flipped = 0 ^ 4 = 4 → prefixCount[4] = 0 → no change
i = 3 → flipped = 0 ^ 8 = 8 → prefixCount[8] = 0 → no change
i = 4 → flipped = 0 ^ 16 = 16 → prefixCount[16] = 0 → no change
i = 5 → flipped = 0 ^ 32 = 32 → prefixCount[32] = 0 → no change
i = 6 → flipped = 0 ^ 64 = 64 → prefixCount[64] = 0 → no change
i = 7 → flipped = 0 ^ 128 = 128 → prefixCount[128] = 0 → no change
i = 8 → flipped = 0 ^ 256 = 256 → prefixCount[256] = 0 → no change
i = 9 → flipped = 0 ^ 512 = 512 → prefixCount[512] = 0 → no change
Step 8: Update prefix count
prefixCount[0] += 1 → prefixCount[0] = 3
Step 9: Return the Final Result
Final value of ans = 9
The total number of wonderful substrings for "aabb" is 9.
Code for All Languages
C++
#include <iostream> // For input and output
#include <vector> // For using the vector data structure
#include <string> // For handling strings
using namespace std;
class Solution {
public:
long long wonderfulSubstrings(string word) {
// Step 1: Initialize variables
long long ans = 0; // Stores final result
int n = word.length(); // Length of input word
int bitmask = 0; // Bitmask to track parity of letters 'a'-'j'
// Step 2: Create prefix count array and initialize base case
vector<int> prefixCount(1024, 0); // Possible bitmask states: 2^10 = 1024
prefixCount[0] = 1; // We have seen the "all even" bitmask once
// Step 3: Traverse the string character by character
for (int idx = 0; idx < n; idx++) {
// Step 4: Update the bitmask for current character
int pos = word[idx] - 'a'; // Get position of character in 'a' to 'j'
bitmask ^= (1 << pos); // Flip the bit at that position
// Step 5: Add substrings ending here with all even counts
ans += prefixCount[bitmask];
// Step 6: Loop i = 0 to 9 to check for bitmasks differing by exactly one bit
for (int i = 0; i < 10; i++) {
int flipped = bitmask ^ (1 << i); // Flip the i-th bit
// Step 7: Add substrings differing by exactly one bit
ans += prefixCount[flipped];
}
// Step 8: Update prefix count for current bitmask
prefixCount[bitmask]++;
}
// Step 9: Return the final answer
return ans;
}
};
int main() {
string word;
cin >> word;
Solution sol;
long long result = sol.wonderfulSubstrings(word); // Call the function
// Output the result
cout << result << endl;
return 0;
}
Java
import java.util.*; // For Scanner and Arrays
class Solution {
public long wonderfulSubstrings(String word) {
// Step 1: Initialize variables
long ans = 0; // Stores final result
int n = word.length(); // Length of the input word
int bitmask = 0; // Tracks parity (odd/even) of letters 'a'-'j'
// Step 2: Create prefix count array and initialize base case
int[] prefixCount = new int[1024]; // 2^10 = 1024 possible bitmask states
prefixCount[0] = 1; // We've seen the "all even" bitmask once
// Step 3: Traverse the string character by character
for (int idx = 0; idx < n; idx++) {
// Step 4: Update the bitmask for current character
int pos = word.charAt(idx) - 'a'; // Get position of character in 'a' to 'j'
bitmask ^= (1 << pos); // Flip the bit at that position
// Step 5: Add substrings ending here with all even counts
ans += prefixCount[bitmask];
// Step 6: Loop i = 0 to 9 to check for bitmasks differing by exactly one bit
for (int i = 0; i < 10; i++) {
int flipped = bitmask ^ (1 << i); // Flip the i-th bit
// Step 7: Add substrings differing by exactly one bit
ans += prefixCount[flipped];
}
// Step 8: Update prefix count for current bitmask
prefixCount[bitmask]++;
}
// Step 9: Return the final answer
return ans;
}
}
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
// Input the string (no prompt, as per format)
String word = sc.next();
Solution sol = new Solution();
long result = sol.wonderfulSubstrings(word); // Call the function
// Output the result
System.out.println(result);
}
}
Python
class Solution:
def wonderfulSubstrings(self, word: str) -> int:
# Step 1: Initialize variables
count = 0 # Stores the final result
n = len(word) # Length of the input word
bitmask = 0 # Tracks parity (odd/even) of letters 'a' to 'j'
# Step 2: Create prefix count array and initialize base case
prefixCount = [0] * 1024 # There are 2^10 possible bitmask states
prefixCount[0] = 1 # We've seen the "all even counts" bitmask once
# Step 3: Traverse the string character by character
for ch in word:
# Step 4: Update the bitmask for current character
pos = ord(ch) - ord('a') # Get position of character ('a'-'j')
bitmask ^= (1 << pos) # Flip the bit at that position
# Step 5: Add substrings ending here with all even counts
count += prefixCount[bitmask]
# Step 6: Loop i = 0 to 9 to check for bitmasks differing by exactly one bit
for i in range(10):
flipped = bitmask ^ (1 << i)
# Step 7: Add substrings differing by exactly one bit
count += prefixCount[flipped]
# Step 8: Update prefix count for current bitmask
prefixCount[bitmask] += 1
# Step 9: Return the final result
return count
# Driver Code
if __name__ == "__main__":
word = input() # Input the string
sol = Solution()
result = sol.wonderfulSubstrings(word) # Call the function
# Output the result
print(result)
Javascript
/**
* @param {string} word - The input string consisting of letters from 'a' to 'j'
* @return {number} - Total number of wonderful substrings
*/
var wonderfulSubstrings = function(word) {
// Step 1: Initialize variables
let count = 0; // Stores the final result
const n = word.length;
let bitmask = 0; // Tracks parity (odd/even) of letters 'a' to 'j'
// Step 2: Create prefix count array and initialize base case
let prefixCount = new Array(1024).fill(0); // 2^10 possible states
prefixCount[0] = 1; // The "all even" state is seen once at start
// Step 3: Traverse the string character by character
for (let ch of word) {
// Step 4: Update the bitmask for current character
let pos = ch.charCodeAt(0) - 'a'.charCodeAt(0);
bitmask ^= (1 << pos);
// Step 5: Add substrings ending here with all even counts
count += prefixCount[bitmask];
// Step 6: Loop i = 0 to 9 to check for bitmasks differing by exactly one bit
for (let i = 0; i < 10; i++) {
let flipped = bitmask ^ (1 << i);
// Step 7: Add substrings differing by exactly one bit
count += prefixCount[flipped];
}
// Step 8: Update prefix count for current bitmask
prefixCount[bitmask]++;
}
// Step 9: Return the final result
return count;
};
// Driver code
const readline = require("readline");
const rl = readline.createInterface({
input: process.stdin,
output: process.stdout
});
let inputs = [];
rl.on("line", function(line) {
inputs.push(line.trim());
if (inputs.length === 1) {
const word = inputs[0];
const result = wonderfulSubstrings(word);
console.log(result);
rl.close();
}
});
Time Complexity: O(n)
Outer Loop: O(n)
The main loop runs once for every character in the string word.
Let ,n = length of word
So, the loop executes exactly n times.
Bitmask Update: O(1)
Inside the loop, updating the bitmask for the current character is done by:
- Finding the character’s position (0 to 9)
- Using XOR to flip the corresponding bit
This is a single bitwise operation → O(1) time.
Check for All Even Count: O(1)
Checking how many substrings end here with all even counts is done by:
- Directly adding prefixCount[bitmask] to the answer.
This is a simple array lookup → O(1) time.
Check for One Bit Difference: O(10)
For each position i = 0 to 9, we flip the i-th bit and look up prefixCount[flipped].
- This inner loop always runs 10 times (for letters 'a' to 'j').
- Each iteration is just a bitwise XOR and an array lookup.
So, this part is O(10) = O(1).
Update Prefix Count: O(1)
Incrementing prefixCount[bitmask] is a simple array operation → O(1) time.
Total Time per Character: O(1)
Combining:
- Bitmask update → O(1)
- All even check → O(1)
- One bit difference check → O(10) = O(1)
- Prefix update → O(1)
So, the total work done per character is constant time → O(1).
Final Time Complexity: O(n)
Since we do O(1) work for each of the n characters, the total time complexity for the solution is: O(n)
Space Complexity: O(1)
Auxiliary Space Complexity: O(1)
This refers to any extra space used by the algorithm that is independent of the input and output sizes.
In this optimized bitmask approach, we create:
- A prefixCount array of size 1024 (because there are 2¹⁰ possible bitmask states for 10 letters).
- A few integer variables: bitmask, ans, and loop counters.
- No additional data structures that grow with input size.
The size of prefixCount is fixed because it depends only on the number of possible bitmask states for the letters 'a' to 'j' — not on the input string length n.
Thus, the auxiliary space complexity is O(1).
Total Space Complexity: O(n)
Input Space:
The input string word of length n → O(n)
Output Space:
The output is a single integer count of wonderful substrings → O(1)
Auxiliary Space: As analyzed above → O(1)
Total Space Complexity = O(n) + O(1) + O(1) = O(n)
Learning Tip
Now we have successfully tackled this problem, let's try these similar problems.
You are given a string s and a positive integer k. Let vowels and consonants be the number of vowels and consonants in a string. A string is beautiful if:
vowels == consonants.
(vowels * consonants) % k == 0, in other terms the multiplication of vowels and consonants is divisible by k.
Return the number of non-empty beautiful substrings in the given string s.
Given an array of integers nums and an integer k. A continuous subarray is called nice if there are k odd numbers on it. Return the number of nice sub-arrays.