Number of Submatrices That Sum to Target Solution In C++/Java/Python/JS
Problem Description
Given a matrix and a target, return the number of non-empty submatrices that sum to target.
What is a Submatrix?
A submatrix x1, y1, x2, y2 is the set of all cells matrix[x][y] with x1 <= x <= x2 and y1 <= y <= y2.
Two submatrices (x1, y1, x2, y2) and (x1', y1', x2', y2') are different if they have some coordinate that is different: for example, if x1 != x1'.
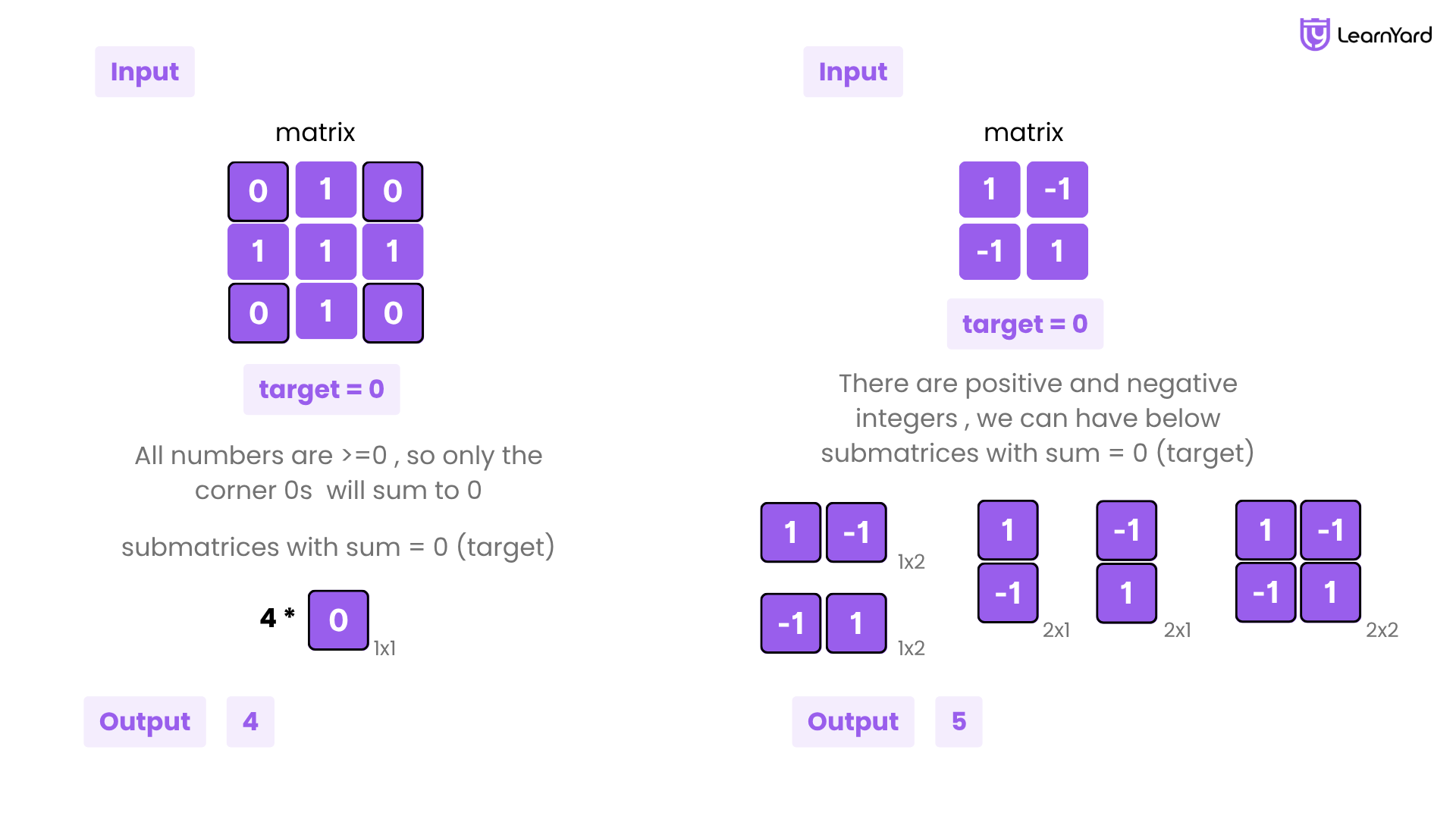
Examples
Input: matrix = [[0,1,0],[1,1,1],[0,1,0]], target = 0
Output: 4
Explanation: The four 1x1 submatrices that only contain 0.
Input: matrix = [[1,-1],[-1,1]], target = 0
Output: 5
Explanation: The two 1x2 submatrices, plus the two 2x1 submatrices, plus the 2x2 submatrix.
Input: matrix = [[904]], target = 0
Output: 0
Explanation: There is only 1 submatrix and its sum is not equal to target.
Constraints
- 1 <= matrix.length <= 100
- 1 <= matrix[0].length <= 100
- -1000 <= matrix[i][j] <= 1000
- -10^8 <= target <= 10^8
The very first question that comes to our mind after reading the problem is: How can we identify all submatrices whose sum equals the target value? Most of us already know that one straightforward way is to examine every possible submatrix within the given matrix and calculate its sum directly to see if it matches the target. To build a solid understanding, let's start by exploring this brute-force approach in detail. This will help us grasp the core concept clearly before moving on to more optimized solutions.
Brute-Force Approach
Intuition
The problem asks us to count all submatrices in a 2D matrix whose sum is equal to a target value. The simplest solution that comes to our mind is to check every possible submatrix within the given matrix and calculate its sum directly to see if it matches the target
At first glance, this might sound complicated, because submatrices can be of many different shapes and sizes.
But lets simplify it by first understanding what a submatrix is?
A submatrix is simply a rectangular region within the matrix, defined by two corners: Top Left corner and Bottom Right corner
Any submatrix can be represented by choosing these two corners.
How can we find all possible submatrices?
To cover all possible rectangles in a matrix of size n × m, we can use a systematic approach:
We fix a starting row index start_row, where start_row ranges from 0 to n - 1.
We fix a starting column index start_col, where start_col ranges from 0 to m - 1.
For each starting cell (start_row, start_col), we then explore all possible rectangles that begin at this cell by:
Choosing an ending row index end_row, where end_row ranges from start_row to n - 1.
Choosing an ending column index end_col, where end_col ranges from start_col to m - 1.
By doing this, we systematically generate every possible submatrix in the grid:
- Each rectangle is uniquely defined by its top-left corner (start_row, start_col) and its bottom-right corner (end_row, end_col).
- Every choice of (start_row, start_col, end_row, end_col) corresponds to exactly one valid submatrix.
This method ensures we cover all rectangles exactly once — no duplicates, and none are missed.
Now for a particular submatrix, we will use two nested loops to accumulate the sum of all the elements in this submatrix to a variable sum.
After obtaining the sum of all elements in the submatrix , we check if sum is equal to target. If yes then we increment the ans variable that would store the number of submatrices that sum to target.
Finally, after checking each submatrix, we return ans.
Approach
Step 1: Initialize the answer variable
Create a variable ans to store the total count of submatrices whose sum equals the target.
Set ans = 0 initially.
Step 2: Loop to fix the starting row of the current submatrix
Use an outer loop where start_row ranges from 0 to n - 1 (where n is the number of rows).
This loop picks every possible starting row for the submatrix.
Step 3: Loop to fix the starting column of the current submatrix
For each start_row, use another loop where start_col ranges from 0 to m - 1 (where m is the number of columns).
This loop picks every possible starting column for the submatrix.
Step 4: Loop to fix the ending row of the current submatrix
For each starting point (start_row, start_col), use a loop end_row that ranges from start_row to n - 1.
This selects all possible bottom edges of the submatrix.
Step 5: Loop to fix the ending column of the current submatrix
For each chosen end_row, use another loop end_col ranging from start_col to m - 1.
This picks all possible right edges, forming a unique bottom-right corner (end_row, end_col).
Step 6: Initialize variable sum to store sum of elements of current submatrix
Before computing, create sum = 0 to accumulate the sum of elements in this submatrix.
Step 7: Loop through the rows of the current submatrix
Use a loop i from start_row to end_row.
Step 8: Loop through the columns of the current submatrix
Inside that, use a loop j from start_col to end_col.
Step 9: Add the current element of submatrix to the sum
For each cell (i, j) inside the submatrix, do sum += matrix[i][j].
Step 10: Check if sum equals target, if yes increment ans
After computing the sum, check:
If sum == target, increment ans by 1.
Step 11: Return ans as the required value
After all loops have completed, return ans as the final answer.
Dry Run
Let’s do a detailed dry run of the brute-force approach using nested loops
for the input: matrix = [[1, -1], [-1, 1]], target = 0
We want to find the number of non-empty submatrices whose sum equals the target.
Step 1: Understand the matrix
Original matrix: first row has 1, -1; second row has -1, 1
Number of rows (n) = 2
Number of columns (m) = 2
Initialize ans = 0 → this will store the total count of valid submatrices.
Step 2: Use nested loops to choose all possible submatrices
We will:
- Fix the starting row (start_row) from 0 to 1
- Fix the starting column (start_col) from 0 to 1
Then, for each starting cell, choose:
- Ending row (end_row) from start_row to 1
- Ending column (end_col) from start_col to 1
For each submatrix, calculate its sum and check if it matches the target.
Iteration-Wise Dry Run
start_row = 0, start_col = 0
end_row = 0, end_col = 0
Current submatrix contains just the single element 1
Sum = 1
Compare with target = 0 → no match
ans remains 0
end_row = 0, end_col = 1
Current submatrix covers first row, elements 1, -1
Sum = 1 + (-1) = 0
Compare with target = 0 → match
ans += 1 → ans = 1
end_row = 1, end_col = 0
Current submatrix covers first column, elements 1, -1
Sum = 1 + (-1) = 0
Compare with target = 0 → match
ans += 1 → ans = 2
end_row = 1, end_col = 1
Current submatrix covers the entire matrix: first row 1, -1 and second row -1, 1
Sum = 1 + (-1) + (-1) + 1 = 0
Compare with target = 0 → match
ans += 1 → ans = 3
start_row = 0, start_col = 1
end_row = 0, end_col = 1
Current submatrix contains single element -1
Sum = -1
Compare with target = 0 → no match
ans remains 3
end_row = 1, end_col = 1
Current submatrix covers second column, elements -1, 1
Sum = -1 + 1 = 0
Compare with target = 0 → match
ans += 1 → ans = 4
start_row = 1, start_col = 0
end_row = 1, end_col = 0
Current submatrix contains single element -1
Sum = -1
Compare with target = 0 → no match
ans remains 4
end_row = 1, end_col = 1
Current submatrix covers second row, elements -1, 1
Sum = -1 + 1 = 0
Compare with target = 0 → match
ans += 1 → ans = 5
start_row = 1, start_col = 1
end_row = 1, end_col = 1
Current submatrix contains single element 1
Sum = 1
Compare with target = 0 → no match
ans remains 5
Final Result
Total number of non-empty submatrices that sum to target (0): ans = 5
These 5 submatrices are:
- Rows 0–0, columns 0–1 (first row, both columns)
- Rows 0–1, columns 0–0 (first column, both rows)
- Rows 0–1, columns 0–1 (whole matrix)
- Rows 0–1, columns 1–1 (second column, both rows)
- Rows 1–1, columns 0–1 (second row, both columns)
Code for All Languages
C++
#include <iostream> // For input and output
#include <vector> // For using vector
using namespace std;
class Solution {
public:
int numSubmatrixSumTarget(vector<vector<int>>& matrix, int target) {
int n = matrix.size(); // Number of rows
int m = matrix[0].size(); // Number of columns
int ans = 0; // Step 1: Initialize answer to store total count
// Step 2: Loop to fix the starting row
for (int start_row = 0; start_row < n; start_row++) {
// Step 3: Loop to fix the starting column
for (int start_col = 0; start_col < m; start_col++) {
// Step 4: Loop to fix the ending row
for (int end_row = start_row; end_row < n; end_row++) {
// Step 5: Loop to fix the ending column
for (int end_col = start_col; end_col < m; end_col++) {
int sum = 0; // Step 6: Initialize sum for current submatrix
// Step 7: Loop through the rows of current submatrix
for (int i = start_row; i <= end_row; i++) {
// Step 8: Loop through the columns of current submatrix
for (int j = start_col; j <= end_col; j++) {
sum += matrix[i][j]; // Step 9: Add current element to sum
}
}
// Step 10: Check if sum equals target, if yes increment ans
if (sum == target) {
ans++;
}
}
}
}
}
// Step 11: Return final answer
return ans;
}
};
int main() {
int n, m, target;
cin >> n >> m >> target; // Input number of rows, columns, and target
vector<vector<int>> matrix(n, vector<int>(m));
// Input the matrix elements
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
cin >> matrix[i][j];
}
}
Solution sol;
int result = sol.numSubmatrixSumTarget(matrix, target);
// Output the result
cout << result << endl;
return 0;
}
Java
import java.util.*; // For Scanner
class Solution {
public int numSubmatrixSumTarget(int[][] matrix, int target) {
int n = matrix.length; // Number of rows
int m = matrix[0].length; // Number of columns
int ans = 0; // Step 1: Initialize answer to store total count
// Step 2: Loop to fix the starting row
for (int start_row = 0; start_row < n; start_row++) {
// Step 3: Loop to fix the starting column
for (int start_col = 0; start_col < m; start_col++) {
// Step 4: Loop to fix the ending row
for (int end_row = start_row; end_row < n; end_row++) {
// Step 5: Loop to fix the ending column
for (int end_col = start_col; end_col < m; end_col++) {
int sum = 0; // Step 6: Initialize sum for current submatrix
// Step 7: Loop through the rows of current submatrix
for (int i = start_row; i <= end_row; i++) {
// Step 8: Loop through the columns of current submatrix
for (int j = start_col; j <= end_col; j++) {
sum += matrix[i][j]; // Step 9: Add current element to sum
}
}
// Step 10: Check if sum equals target, if yes increment ans
if (sum == target) {
ans++;
}
}
}
}
}
// Step 11: Return final answer
return ans;
}
}
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
// Input number of rows, columns, and target
int n = sc.nextInt();
int m = sc.nextInt();
int target = sc.nextInt();
int[][] matrix = new int[n][m];
// Input the matrix elements
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
matrix[i][j] = sc.nextInt();
}
}
Solution sol = new Solution();
int result = sol.numSubmatrixSumTarget(matrix, target);
// Output the result
System.out.println(result);
}
}
Python
from typing import List # For specifying the type hints
class Solution:
def numSubmatrixSumTarget(self, matrix: List[List[int]], target: int) -> int:
n = len(matrix) # Number of rows
m = len(matrix[0]) # Number of columns
ans = 0 # Step 1: Initialize answer to store total count
# Step 2: Loop to fix the starting row
for start_row in range(n):
# Step 3: Loop to fix the starting column
for start_col in range(m):
# Step 4: Loop to fix the ending row
for end_row in range(start_row, n):
# Step 5: Loop to fix the ending column
for end_col in range(start_col, m):
sum_ = 0 # Step 6: Initialize sum for current submatrix
# Step 7: Loop through the rows of current submatrix
for i in range(start_row, end_row + 1):
# Step 8: Loop through the columns of current submatrix
for j in range(start_col, end_col + 1):
sum_ += matrix[i][j] # Step 9: Add current element to sum
# Step 10: Check if sum equals target, if yes increment ans
if sum_ == target:
ans += 1
# Step 11: Return final answer
return ans
# Driver code
if __name__ == "__main__":
n, m, target = map(int, input().split()) # Input number of rows, columns, and target
matrix = []
# Input the matrix elements
for _ in range(n):
row = list(map(int, input().split()))
matrix.append(row)
sol = Solution()
result = sol.numSubmatrixSumTarget(matrix, target)
# Output the result
print(result)
Javascript
/**
* @param {number[][]} matrix
* @param {number} target
* @return {number}
*/
var numSubmatrixSumTarget = function(matrix, target) {
const n = matrix.length; // Number of rows
const m = matrix[0].length; // Number of columns
let ans = 0; // Step 1: Initialize answer to store total count
// Step 2: Loop to fix the starting row
for (let start_row = 0; start_row < n; start_row++) {
// Step 3: Loop to fix the starting column
for (let start_col = 0; start_col < m; start_col++) {
// Step 4: Loop to fix the ending row
for (let end_row = start_row; end_row < n; end_row++) {
// Step 5: Loop to fix the ending column
for (let end_col = start_col; end_col < m; end_col++) {
let sum = 0; // Step 6: Initialize sum for current submatrix
// Step 7: Loop through the rows of current submatrix
for (let i = start_row; i <= end_row; i++) {
// Step 8: Loop through the columns of current submatrix
for (let j = start_col; j <= end_col; j++) {
sum += matrix[i][j]; // Step 9: Add current element to sum
}
}
// Step 10: Check if sum equals target, if yes increment ans
if (sum === target) {
ans += 1;
}
}
}
}
}
// Step 11: Return final answer
return ans;
};
// Driver code
const readline = require("readline");
const rl = readline.createInterface({
input: process.stdin,
output: process.stdout
});
let inputs = [];
let n, m, target;
rl.on("line", function(line) {
inputs.push(line.trim());
if (inputs.length === 1) {
// First line contains n, m, and target
[n, m, target] = inputs[0].split(' ').map(Number);
} else if (inputs.length === n + 1) {
// We have read all n rows
const matrix = [];
for (let i = 1; i <= n; i++) {
const row = inputs[i].split(' ').map(Number);
matrix.push(row);
}
const result = numSubmatrixSumTarget(matrix, target);
console.log(result);
rl.close();
}
});
Time Complexity: O(n³ * m³)
Let us denote:
- n = number of rows in the matrix
- m = number of columns in the matrix
Outer Loops for Starting Indices: O(n * m)
We fix the starting row index start_row, which runs from 0 to n − 1 (total n choices).
For each start_row, we fix the starting column index start_col, which runs from 0 to m − 1 (total m choices).
Together, these two nested loops run in O(n * m) time.
Inner Loops for Ending Indices: O(n * m)
For every fixed starting point (start_row, start_col), we choose the ending row index end_row, which runs from start_row to n − 1 (up to n choices).
We also choose the ending column index end_col, which runs from start_col to m − 1 (up to m choices).
So, these two nested loops also run together in O(n * m) time.
Calculating Sum for Each Submatrix: O(n * m)
For each submatrix defined by (start_row, start_col, end_row, end_col), we calculate the sum by looping through all its cells.
The largest possible submatrix could cover the entire matrix, containing up to n * m cells.
So, computing the sum for one submatrix takes O(n * m) time in the worst case.
Total Time per Submatrix: O(n * m)
For each submatrix, we spend O(n * m) time:
- Looping through its cells to compute the sum
- Comparing the sum with the target and possibly incrementing the answer
Final Time Complexity: O(n² * m² * n * m)
Putting it all together:
- O(n * m) choices for the starting point (start_row, start_col)
- O(n * m) choices for the ending point (end_row, end_col)
- O(n * m) time to compute the sum for each submatrix
So, the total time complexity becomes:
O(n * m) × O(n * m) × O(n * m) = O(n³ * m³)
Space Complexity: O(1)
Auxiliary Space Complexity: O(1)
This refers to the extra space used by the algorithm itself, excluding the input and output.
In the brute-force approach, we only use a few integer variables: ans, sum, and loop counters.
Because we do not allocate any extra space that depends on the size of the matrix, the auxiliary space used stays constant.
So, the auxiliary space complexity is O(1).
Total Space Complexity: O(n * m)
This accounts for:
- Input space: The input matrix itself of size n × m, which takes O(n * m).
- Output space: The answer variable ans, which is a single integer → O(1).
- Extra auxiliary space used by the algorithm itself → O(1).
Adding these together:
Total Space Complexity=O(n∗m)+O(1)=O(n∗m)
Why this Approach will give TLE?
The main reason this brute-force approach will give a Time Limit Exceeded (TLE) error is because of its extremely high time complexity, especially when the input matrix is large.
Let’s break this down:
- For a matrix of size up to 100 × 100, we try every possible submatrix.
- Each submatrix is defined by choosing two rows (start_row and end_row)and two columns (start_col and end_col).
- So, total number of possible submatrices is approximately:
100 × 100 × 100 × 100 = 10^8 submatrices.
For each of these submatrices, the brute-force code computes the sum by explicitly looping over all the cells inside the submatrix:
- In the worst case, the submatrix might be the entire matrix itself (100 × 100), so computing its sum can take up to:
100 × 100 = 10,000 = 10^4 operations.
So, the total worst-case number of operations is:
- Number of submatrices × operations per sum
- ≈ 10^8 × 10^4 = 10^12 operations
This is an enormous number (one trillion operations).
Most competitive programming platforms (like LeetCode, Codeforces, etc.) typically allow programs to run within 1–2 seconds, which roughly means your solution must finish within about 10^7–10^8 operations.
Since the brute-force approach can go up to 10^12 operations, it is far beyond the time limits, and thus it will inevitably get TLE on larger matrices.
We’ve seen the brute-force approach that checks every submatrix by recalculating its sum cell by cell—but this quickly becomes too slow due to the huge number of submatrices. Instead of recomputing each sum, can we reuse previously computed sums to cut down on redundant work and remove the deepest loops? Let’s explore how.
Better Approach
Intuition
In the brute-force approach, the biggest slowdown came from recalculating the sum of every submatrix by iterating over each cell inside it. While correct, this leads to huge time complexity because the same cells get summed many times for overlapping submatrices.
To optimize this, let’s think differently: what if we could precompute sums so that instead of summing each submatrix from scratch, we could get its sum in constant time? This is exactly what the 2D prefix sum (or cumulative sum) technique helps us achieve.
A 2D prefix sum matrix is built such that each cell (i, j) contains the sum of the rectangle from the top-left corner (0, 0) to (i, j).
In other words, prefixSum[i][j] tells us the total sum of all elements above and to the left of (i, j), including (i, j) itself.
Formally:
prefixSum[i][j] = sum of matrix[0][0] to matrix[i][j]
By precomputing this, we can calculate the sum of any submatrix defined by its top-left (x1, y1) and bottom-right (x2, y2) corners in constant time O(1) using the inclusion-exclusion principle:
sum of submatrix with top-left (x1, y1) and bottom-right (x2, y2) = prefixSum[x2][y2] - prefixSum[x1 - 1][y2] (if x1 > 0) - prefixSum[x2][y1 - 1] (if y1 > 0) + prefix[x1 - 1][y1 - 1] (if x1 > 0 and y1 > 0)
How to construct the prefixSum matrix?
To efficiently compute the sum of any submatrix in constant time, we build a 2D prefix sum matrix.
Each cell prefixSum[i][j] represents the sum of all elements from the top-left corner (0,0) to the cell (i,j).
Step by step process:
- Initialize the prefixSum matrix
Create a new matrix prefixSum of the same size as the original matrix, initially filled with zeros. - Process each cell (i,j) row by row
For each cell (i,j) in the matrix, compute: prefixSum[i][j] = matrix[i][j]+prefixSum[i-1][j] (the sum from the cell above, or 0 if i == 0)
+ prefixSum[i][j-1] (the sum from the cell to the left, or 0 if j == 0)
- prefixSum[i-1][j-1] (to remove the overlap that was added twice; or 0 if i == 0 or j == 0)
Special cases:
- If i == 0, then prefix[i-1][j] is treated as 0.
- If j == 0, then prefix[i][j-1] is treated as 0.
- For the very first cell (0,0), we directly set prefix[0][0] = matrix[0][0].
Why subtract prefix[i-1][j-1]?
When adding the top part (prefix[i-1][j]) and the left part (prefix[i][j-1]), the top-left overlap region (prefix[i-1][j-1]) gets added twice.
To correct this, we subtract it once.
Result:
After filling the entire prefix sum matrix, each prefix[i][j] tells us the sum of all elements in the rectangle from (0,0) to (i,j).
Computing the sum of any submatrix:
Suppose the submatrix is defined by its top-left corner (top, left) and bottom-right corner (bottom, right).
We use the inclusion-exclusion formula:
sum = prefix[bottom][right]- prefixSum[top-1][right](remove the area above)
- prefixSum[bottom][left-1] (remove the area to the left)
+ prefixSum[top-1][left-1] (add back the overlap that was subtracted twice)
Handling boundaries:
When top == 0 or left == 0, the terms like prefix[top-1][right] or prefix[bottom][left-1] are simply treated as 0.
Now , the advantage that we obtain by computing the prefixSum matrix before iterating for each submatrix of the matrix is that no we do not have to run two nested loops for a submatrix to get the sum of all elements in it, rather we can get it in O(1) by using the formula above.
So Initially we have to run two nested loops to precompute the prefixSum matrix, after that we can have 4 nested loops to fix the start row, start column, end row and end column and then check if the sum of all the elements in this submatrix is equal to target or not by utilizing the prefixSum matrix in O(1) time significantly improving the time.
Approach
Step 1: Initialize the answer variable
Create a variable ans to store the total count of submatrices whose sum equals the target.
Initially set ans = 0.
Step 2: Create 2D prefixSum matrix and initialize
Construct a prefixSum matrix of the same size as the input matrix, initialized with zeros.
Each cell prefixSum[i][j] will later store the sum of all elements from the top-left corner (0,0) to cell (i,j).
Step 3: Loop to fix the current row to fill prefixSum
Use an outer loop i that goes from 0 to n - 1 (where n is the number of rows in the matrix).
Step 4: Loop to fix the current column to fill prefixSum
Inside that, use another loop j that goes from 0 to m - 1 (where m is the number of columns).
Step 5: Populate the current cell of prefixSum
For each cell (i, j), compute prefixSum[i][j] by adding:
– The current cell value matrix[i][j]
– The sum above it: prefixSum[i-1][j] if i > 0
– The sum to its left: prefixSum[i][j-1] if j > 0
– Subtract prefixSum[i-1][j-1] once if both i > 0 and j > 0 to avoid double-counting
This follows the inclusion-exclusion principle.
Step 6: Loop to fix the starting row of the current submatrix
Use a loop start_row from 0 to n - 1 to choose the top edge of each submatrix.
Step 7: Loop to fix the starting column of the current submatrix
For each start_row, use a loop start_col from 0 to m - 1 to pick the left edge.
Step 8: Loop to fix the ending row of the current submatrix
For each chosen top-left corner, use a loop end_row from start_row to n - 1 to pick the bottom edge.
Step 9: Loop to fix the ending column of the current submatrix
Inside that, use a loop end_col from start_col to m - 1 to pick the right edge, forming the bottom-right corner (end_row, end_col).
Step 10: Calculate sum of current submatrix using prefixSum by inclusion-exclusion principle
For the submatrix defined by (start_row, start_col) and (end_row, end_col):
– Start with prefixSum[end_row][end_col]
– Subtract prefixSum[start_row-1][end_col] if start_row > 0
– Subtract prefixSum[end_row][start_col-1] if start_col > 0
– Add back prefixSum[start_row-1][start_col-1] if both start_row > 0 and start_col > 0
Step 11: If sum is equal to target, increment ans
If the computed sum == target, increase ans by 1.
Step 12: Return ans as the required value
After checking all possible submatrices, return ans as the final count of submatrices whose sum equals target.
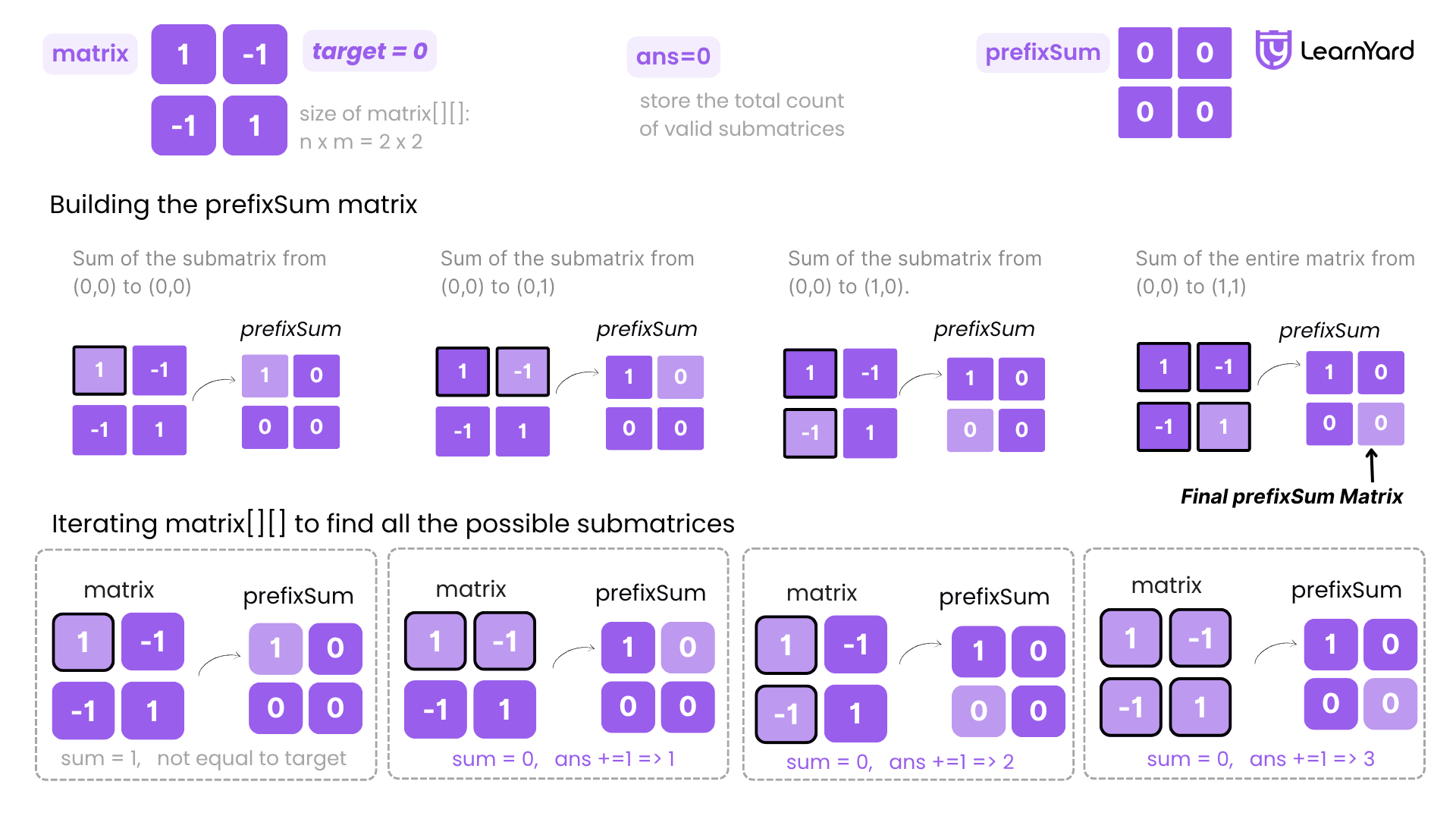
Dry Run
Let’s do a detailed dry run of the prefix sum approach using nested loops and inclusion-exclusion
for the input: matrix = [[1, -1], [-1, 1]], target = 0
We want to find the number of non-empty submatrices whose sum equals the target.
Step 1: Understand the matrix
Original matrix: first row has 1, -1; second row has -1, 1
Number of rows (n) = 2
Number of columns (m) = 2
Initialize ans = 0 → this will store the total count of valid submatrices.
Step 2: Build the prefixSum matrix
We construct a prefixSum matrix of size 2×2.
prefixSum[0][0] = matrix[0][0] = 1
prefixSum[0][1] = prefixSum[0][0] + matrix[0][1] = 1 + (-1) = 0
prefixSum[1][0] = prefixSum[0][0] + matrix[1][0] = 1 + (-1) = 0
prefixSum[1][1] = matrix[1][1] + prefixSum[0][1] + prefixSum[1][0] - prefixSum[0][0]
= 1 + 0 + 0 - 1 = 0
Final prefixSum matrix:
first row: 1, 0
second row: 0, 0
Step 3: Use nested loops to choose all possible submatrices
We will:
Fix the starting row (start_row) from 0 to 1
Fix the starting column (start_col) from 0 to 1
For each starting cell, choose:
Ending row (end_row) from start_row to 1
Ending column (end_col) from start_col to 1
For each submatrix, calculate sum using inclusion-exclusion on prefixSum and check if it matches the target.
Iteration-Wise Dry Run
start_row = 0, start_col = 0
end_row = 0, end_col = 0
Single element at (0,0): use prefixSum[0][0] = 1
Sum = 1
Compare with target = 0 → no match
ans remains 0
end_row = 0, end_col = 1
Use prefixSum[0][1] = 0
Since start_row=0, start_col=0, no subtraction needed.
Sum = 0
Compare with target = 0 → match
ans += 1 → ans = 1
end_row = 1, end_col = 0
Use prefixSum[1][0] = 0
No subtraction needed.
Sum = 0
Compare with target = 0 → match
ans += 1 → ans = 2
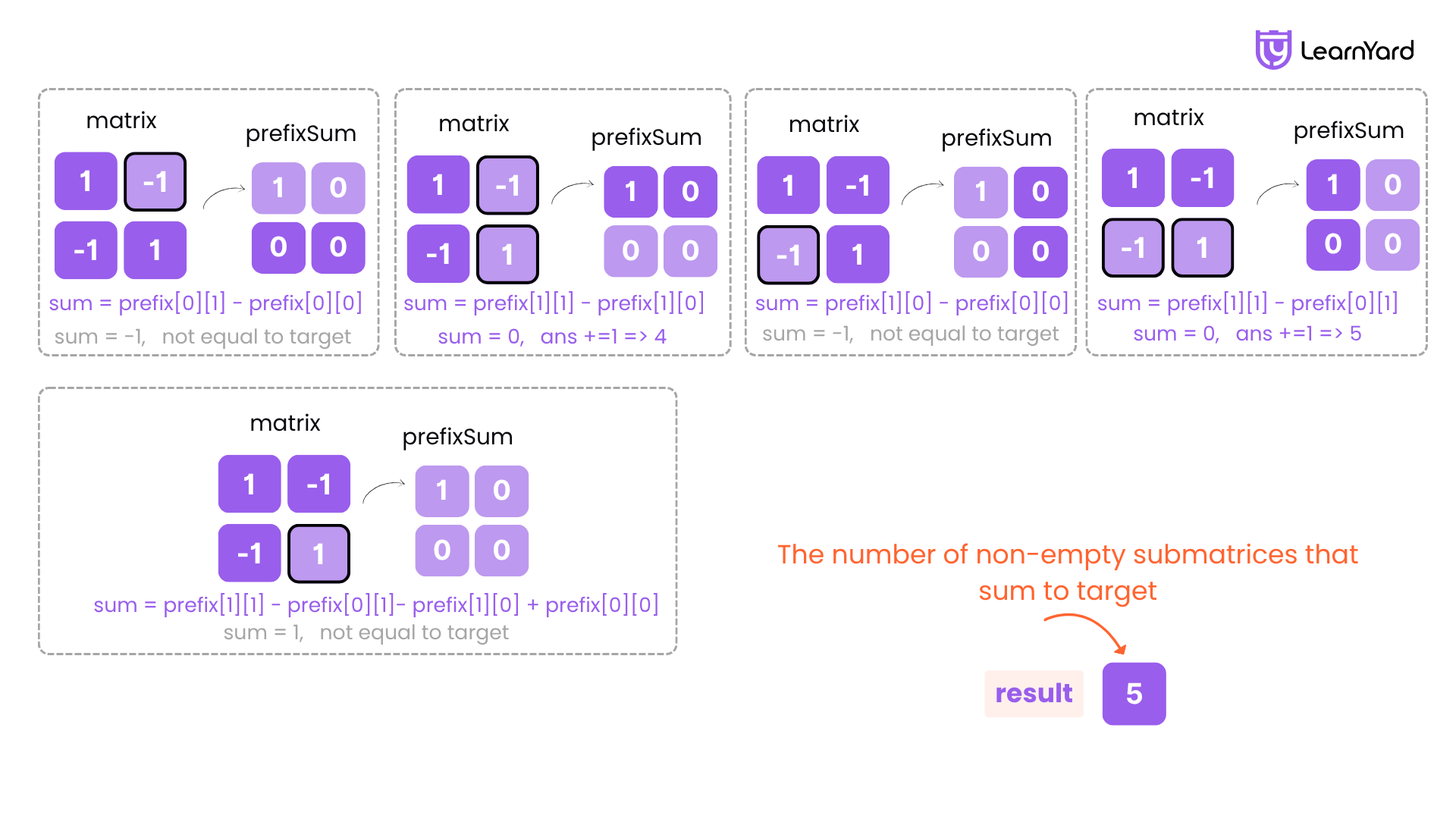
end_row = 1, end_col = 1
Use prefixSum[1][1] = 0
No subtraction needed.
Sum = 0
Compare with target = 0 → match
ans += 1 → ans = 3
start_row = 0, start_col = 1
end_row = 0, end_col = 1
prefixSum[0][1]=0; subtract prefixSum[0][0]=1 (since start_col-1=0).
Sum = 0 - 1 = -1
Compare with target = 0 → no match
ans remains 3
end_row = 1, end_col = 1
prefixSum[1][1]=0; subtract prefixSum[1][0]=0.
Sum = 0 - 0 = 0
Compare with target = 0 → match
ans += 1 → ans = 4
start_row = 1, start_col = 0
end_row = 1, end_col = 0
prefixSum[1][0]=0; subtract prefixSum[0][0]=1 (since start_row-1=0).
Sum = 0 - 1 = -1
Compare with target = 0 → no match
ans remains 4
end_row = 1, end_col = 1
prefixSum[1][1]=0; subtract prefixSum[0][1]=0.
Sum = 0 - 0 = 0
Compare with target = 0 → match
ans += 1 → ans = 5
start_row = 1, start_col = 1
end_row = 1, end_col = 1
prefixSum[1][1]=0; subtract prefixSum[0][1]=0 and prefixSum[1][0]=0; add back prefixSum[0][0]=1.
Sum = 0 - 0 - 0 + 1 = 1
Compare with target = 0 → no match
ans remains 5
Final Result
Total number of non-empty submatrices that sum to target (0): ans = 5
These 5 submatrices are:
Rows 0–0, columns 0–1 (first row, both columns)
Rows 0–1, columns 0–0 (first column, both rows)
Rows 0–1, columns 0–1 (whole matrix)
Rows 0–1, columns 1–1 (second column, both rows)
Rows 1–1, columns 0–1 (second row, both columns)
Code for All Languages
C++
#include <iostream> // For input and output
#include <vector> // For using vector
using namespace std;
class Solution {
public:
int numSubmatrixSumTarget(vector<vector<int>>& matrix, int target) {
int n = matrix.size(); // Number of rows
int m = matrix[0].size(); // Number of columns
// Step 1: Initialize the answer variable
int ans = 0;
// Step 2: Create 2D prefixSum matrix and initialize
vector<vector<int>> prefixSum(n, vector<int>(m, 0));
// Step 3: Loop to fix the current row to fill prefixSum
for (int i = 0; i < n; i++) {
// Step 4: Loop to fix the current column to fill prefixSum
for (int j = 0; j < m; j++) {
// Step 5: Populate the current cell of prefixSum
prefixSum[i][j] = matrix[i][j];
if (i > 0) prefixSum[i][j] += prefixSum[i - 1][j]; // sum above
if (j > 0) prefixSum[i][j] += prefixSum[i][j - 1]; // sum to the left
if (i > 0 && j > 0) prefixSum[i][j] -= prefixSum[i - 1][j - 1]; // subtract overlap
}
}
// Step 6: Loop to fix the starting row of the current submatrix
for (int start_row = 0; start_row < n; start_row++) {
// Step 7: Loop to fix the starting column of the current submatrix
for (int start_col = 0; start_col < m; start_col++) {
// Step 8: Loop to fix the ending row of the current submatrix
for (int end_row = start_row; end_row < n; end_row++) {
// Step 9: Loop to fix the ending column of the current submatrix
for (int end_col = start_col; end_col < m; end_col++) {
// Step 10: Calculate sum of current submatrix using inclusion-exclusion principle
int sum = prefixSum[end_row][end_col];
if (start_row > 0) sum -= prefixSum[start_row - 1][end_col];
if (start_col > 0) sum -= prefixSum[end_row][start_col - 1];
if (start_row > 0 && start_col > 0) sum += prefixSum[start_row - 1][start_col - 1];
// Step 11: If sum is equal to target, increment ans
if (sum == target) {
ans++;
}
}
}
}
}
// Step 12: Return ans as the required value
return ans;
}
};
int main() {
int n, m, target;
cin >> n >> m >> target; // Input number of rows, columns, and target
vector<vector<int>> matrix(n, vector<int>(m));
// Input the matrix elements
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
cin >> matrix[i][j];
}
}
Solution sol;
int result = sol.numSubmatrixSumTarget(matrix, target);
// Output the result
cout << result << endl;
return 0;
}
Java
import java.util.*; // For Scanner
class Solution {
public int numSubmatrixSumTarget(int[][] matrix, int target) {
int n = matrix.length; // Number of rows
int m = matrix[0].length; // Number of columns
// Step 1: Initialize the answer variable
int ans = 0;
// Step 2: Create 2D prefixSum matrix and initialize
int[][] prefixSum = new int[n][m];
// Step 3: Loop to fix the current row to fill prefixSum
for (int i = 0; i < n; i++) {
// Step 4: Loop to fix the current column to fill prefixSum
for (int j = 0; j < m; j++) {
// Step 5: Populate the current cell of prefixSum
prefixSum[i][j] = matrix[i][j];
if (i > 0) prefixSum[i][j] += prefixSum[i - 1][j]; // sum above
if (j > 0) prefixSum[i][j] += prefixSum[i][j - 1]; // sum to the left
if (i > 0 && j > 0) prefixSum[i][j] -= prefixSum[i - 1][j - 1]; // subtract overlap
}
}
// Step 6: Loop to fix the starting row of the current submatrix
for (int start_row = 0; start_row < n; start_row++) {
// Step 7: Loop to fix the starting column of the current submatrix
for (int start_col = 0; start_col < m; start_col++) {
// Step 8: Loop to fix the ending row of the current submatrix
for (int end_row = start_row; end_row < n; end_row++) {
// Step 9: Loop to fix the ending column of the current submatrix
for (int end_col = start_col; end_col < m; end_col++) {
// Step 10: Calculate sum of current submatrix using inclusion-exclusion principle
int sum = prefixSum[end_row][end_col];
if (start_row > 0) sum -= prefixSum[start_row - 1][end_col];
if (start_col > 0) sum -= prefixSum[end_row][start_col - 1];
if (start_row > 0 && start_col > 0) sum += prefixSum[start_row - 1][start_col - 1];
// Step 11: If sum is equal to target, increment ans
if (sum == target) {
ans++;
}
}
}
}
}
// Step 12: Return ans as the required value
return ans;
}
}
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
// Input number of rows, columns, and target
int n = sc.nextInt();
int m = sc.nextInt();
int target = sc.nextInt();
int[][] matrix = new int[n][m];
// Input the matrix elements
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
matrix[i][j] = sc.nextInt();
}
}
Solution sol = new Solution();
int result = sol.numSubmatrixSumTarget(matrix, target);
// Output the result
System.out.println(result);
}
}
Python
from typing import List # For specifying the type hints
class Solution:
def numSubmatrixSumTarget(self, matrix: List[List[int]], target: int) -> int:
n = len(matrix) # Number of rows
m = len(matrix[0]) # Number of columns
# Step 1: Initialize the answer variable
ans = 0
# Step 2: Create 2D prefixSum matrix and initialize
prefixSum = [[0] * m for _ in range(n)]
# Step 3: Loop to fix the current row to fill prefixSum
for i in range(n):
# Step 4: Loop to fix the current column to fill prefixSum
for j in range(m):
# Step 5: Populate the current cell of prefixSum
prefixSum[i][j] = matrix[i][j]
if i > 0:
prefixSum[i][j] += prefixSum[i - 1][j] # sum above
if j > 0:
prefixSum[i][j] += prefixSum[i][j - 1] # sum to the left
if i > 0 and j > 0:
prefixSum[i][j] -= prefixSum[i - 1][j - 1] # subtract overlap
# Step 6: Loop to fix the starting row of the current submatrix
for start_row in range(n):
# Step 7: Loop to fix the starting column of the current submatrix
for start_col in range(m):
# Step 8: Loop to fix the ending row of the current submatrix
for end_row in range(start_row, n):
# Step 9: Loop to fix the ending column of the current submatrix
for end_col in range(start_col, m):
# Step 10: Calculate sum of current submatrix using inclusion-exclusion principle
sum_ = prefixSum[end_row][end_col]
if start_row > 0:
sum_ -= prefixSum[start_row - 1][end_col]
if start_col > 0:
sum_ -= prefixSum[end_row][start_col - 1]
if start_row > 0 and start_col > 0:
sum_ += prefixSum[start_row - 1][start_col - 1]
# Step 11: If sum is equal to target, increment ans
if sum_ == target:
ans += 1
# Step 12: Return ans as the required value
return ans
# Driver code
if __name__ == "__main__":
n, m, target = map(int, input().split()) # Input number of rows, columns, and target
matrix = []
# Input the matrix elements
for _ in range(n):
row = list(map(int, input().split()))
matrix.append(row)
sol = Solution()
result = sol.numSubmatrixSumTarget(matrix, target)
# Output the result
print(result)
Javascript
/**
* @param {number[][]} matrix
* @param {number} target
* @return {number}
*/
var numSubmatrixSumTarget = function(matrix, target) {
const n = matrix.length; // Number of rows
const m = matrix[0].length; // Number of columns
// Step 1: Initialize the answer variable
let ans = 0;
// Step 2: Create 2D prefixSum matrix and initialize
const prefixSum = Array.from({ length: n }, () => Array(m).fill(0));
// Step 3: Loop to fix the current row to fill prefixSum
for (let i = 0; i < n; i++) {
// Step 4: Loop to fix the current column to fill prefixSum
for (let j = 0; j < m; j++) {
// Step 5: Populate the current cell of prefixSum
prefixSum[i][j] = matrix[i][j];
if (i > 0) {
prefixSum[i][j] += prefixSum[i - 1][j]; // sum above
}
if (j > 0) {
prefixSum[i][j] += prefixSum[i][j - 1]; // sum to the left
}
if (i > 0 && j > 0) {
prefixSum[i][j] -= prefixSum[i - 1][j - 1]; // subtract overlap
}
}
}
// Step 6: Loop to fix the starting row of the current submatrix
for (let start_row = 0; start_row < n; start_row++) {
// Step 7: Loop to fix the starting column of the current submatrix
for (let start_col = 0; start_col < m; start_col++) {
// Step 8: Loop to fix the ending row of the current submatrix
for (let end_row = start_row; end_row < n; end_row++) {
// Step 9: Loop to fix the ending column of the current submatrix
for (let end_col = start_col; end_col < m; end_col++) {
// Step 10: Calculate sum of current submatrix using inclusion-exclusion principle
let sum = prefixSum[end_row][end_col];
if (start_row > 0) {
sum -= prefixSum[start_row - 1][end_col];
}
if (start_col > 0) {
sum -= prefixSum[end_row][start_col - 1];
}
if (start_row > 0 && start_col > 0) {
sum += prefixSum[start_row - 1][start_col - 1];
}
// Step 11: If sum is equal to target, increment ans
if (sum === target) {
ans += 1;
}
}
}
}
}
// Step 12: Return ans as the required value
return ans;
};
// Driver code
const readline = require("readline");
const rl = readline.createInterface({
input: process.stdin,
output: process.stdout
});
let inputs = [];
let n, m, target;
rl.on("line", function(line) {
inputs.push(line.trim());
if (inputs.length === 1) {
// First line contains n, m, and target
[n, m, target] = inputs[0].split(' ').map(Number);
} else if (inputs.length === n + 1) {
// We have read all n rows
const matrix = [];
for (let i = 1; i <= n; i++) {
const row = inputs[i].split(' ').map(Number);
matrix.push(row);
}
const result = numSubmatrixSumTarget(matrix, target);
console.log(result);
rl.close();
}
});
Time Complexity: O(n² * m²)
Let us denote:
n = number of rows in the matrix
m = number of columns in the matrix
Building the Prefix Sum Matrix: O(n * m)
We first preprocess the matrix to build a prefix sum matrix.
Each cell (i, j) in the prefix sum can be filled in constant time using previously computed values, so the total time to build this matrix is O(n * m).
Outer Loops for Starting Indices: O(n * m)
We fix the starting row index start_row, which runs from 0 to n − 1 (total n choices).
For each start_row, we fix the starting column index start_col, which runs from 0 to m − 1 (total m choices).
Together, these two nested loops run in O(n * m) time.
Inner Loops for Ending Indices: O(n * m)
For every fixed starting point (start_row, start_col), we choose the ending row index end_row, which runs from start_row to n − 1 (up to n choices).
We also choose the ending column index end_col, which runs from start_col to m − 1 (up to m choices).
These two nested loops together run in O(n * m) time.
Calculating Sum for Each Submatrix: O(1)
For each submatrix defined by (start_row, start_col, end_row, end_col), we compute its sum using the prefix sum matrix in constant time O(1).
Checking if this sum equals the target and updating the answer also takes O(1).
Total Time per Submatrix: O(1)
So, for each submatrix, we spend O(1) time:
– Using the prefix sum to compute the submatrix sum
– Comparing it to the target and possibly incrementing the answer
Final Time Complexity: O(n² * m²)
Putting it all together:
– O(n * m) choices for the starting point (start_row, start_col)
– O(n * m) choices for the ending point (end_row, end_col)
– O(1) time to compute the sum and check against the target
The total time complexity becomes:
O(n * m) × O(n * m) × O(1) = O(n² * m²)
Space Complexity: O(n * m)
This refers to the extra space used by the algorithm itself, excluding the input and output. In this optimized approach using a 2D prefix sum, we create an additional prefixSum matrix of the same size as the original matrix.
So, the auxiliary space used is proportional to the number of cells in the matrix → O(n * m).
Total Space Complexity: O(n * m)
This accounts for:
– Input space: The input matrix itself of size n × m → O(n * m)
– Output space: The answer variable ans, which is a single integer → O(1)
– Extra auxiliary space: The prefix sum matrix we created → O(n * m)
Adding these together, the total space complexity is:
Total Space Complexity = O(n * m) + O(1) + O(n * m) = O(n * m)
Why this Approach will give TLE?
Even after introducing the 2D prefixSum matrix to help us compute the sum of any submatrix faster, this approach still suffers from very high overall time complexity when applied directly with four nested loops.
Let’s understand why:
For a matrix of size up to 100 × 100, we still try every possible submatrix.
Each submatrix is defined by selecting two rows (start_row and end_row) and two columns (start_col and end_col).
So, the total number of possible submatrices remains roughly:
100 × 100 × 100 × 100 = 10^8 submatrices.
Now, thanks to prefixSum, calculating the sum of each submatrix can be done in constant time O(1) instead of explicitly summing over its cells.
But the bottleneck is that we still have to run four nested loops to enumerate all possible top-left and bottom-right corners:
– start_row → end_row
– start_col → end_col
So, the total number of iterations still becomes around 10^8, which by itself is already too large to finish in 1–2 seconds allowed in competitive programming (usually around 10^7–10^8 operations).
Although the prefixSum optimization reduces the cost per submatrix sum check from O(n×m) to O(1), the sheer number of submatrices we must check is so huge (about 100 million) that the total work still exceeds acceptable limits.
As a result, even this better approach with prefixSum will get TLE on larger test cases.
We’ve seen that using 2D prefix sums avoids recalculating sums cell by cell, but it still needs four nested loops to check every submatrix—making it too slow for large inputs. Can we do better by reusing cumulative sums and counting submatrices directly, without iterating over each one? Let’s find out.
Optimal Approach
Intuition
Okay so the better approach was giving TLE since we still needed to consider every possible submatrix and then check for its sum by using 4 nested loops. We somehow need to avoid traversing directly over every possible submatrix. But how do we do so?
Lets see how.
Suppose we decide that every submatrix we care about must start at column start_col and end at column end_col.
By fixing these two columns, each submatrix now stretches only between these two columns — it can still span any number of rows, but its columns are locked.
The submatrices between these two columns just differ in the starting row start_row and ending row end_row.
But if we consider to check for both the starting and ending row for these submatrices, then that would not be optimal. So lets try to think a bit differently.
Lets look at each row between columns , start_col and end_col.
If you add up the numbers in that row from column start_col to end_col, you get a single number for that row.
Do this for every row: you’ll get a new 1D array where each element represents the Sum of numbers in row r between columns start_col and end_col.
After fixing two columns, each such rectangle corresponds to some set of consecutive rows inside this stripe.
Now comes the beautiful part:
If you consider a submatrix between these two fixed columns, its sum is just the sum of some consecutive rows in this new 1D array.
In other words, finding submatrices between columns start_col and end_col whose sum equals the target is exactly the same as finding subarrays in this 1D array whose sum equals the target.
And finding the number of subarrays of an array whose sum is equal to sum target is a standard problem that can be tackled easily.
Okay so now, idea is simple, for each pair of starting column start_col and ending column end_col, we need to find the sum of each row between these columns, add them to a 1D array say nums, and then its just about finding the number of subarrays of this array that sum to target.
Once we decide to fix starting and ending columns, our goal is to quickly find the sum of the part of each row between these two columns.
Imagine you’re at row r and want to get:
sum = matrix[r][start_col] + matrix[r][start_col+1] + ... + matrix[r][end_col]
Doing this naively by looping through every cell in that part of the row would take O(m) time for each row, which becomes too slow when repeated many times.
Solution: Precompute row-wise prefix sums
To speed this up, before starting the main logic, we preprocess the matrix:
For each row, compute a running sum left to right.
Store this in a prefixSum matrix.
So for each cell prefixSum[r][c], it holds the sum of elements in row r from column 0 to column c.
How do we use it?
Now, when we want the sum of row r between columns start_col and end_col:
If start_col== 0, just use: prefixSum[r][start_col]
Else, use: prefixSum[r][end_col] - prefixSum[r][start_col - 1]
This subtraction quickly gives us the sum of the part between columns start_col and end_col in row r — in O(1) time.
Now, how do we find the number of subarrays that would sum to target?
We want to count how many subarrays in nums have sum equal to target.
The easiest way to get the sum of any subarray from index i to j is by using prefix sums:
we precompute prefix[j], the sum of elements from index 0 to j.
To get the sum from index i to j:
– If i > 0, it’s prefix[j] - prefix[i-1]
– If i == 0, it’s simply prefix[j]
So, to find subarrays whose sum is target, we need:
prefix[j] - prefix[i-1] = target
which can be rearranged to:
prefix[i-1] = prefix[j] - target
This means, at every index j, we need to know how many times prefix[j] - target has appeared earlier as a prefix sum.
Instead of checking all previous indices every time (which would be too slow), we keep a hash map that records how many times each prefix sum has been seen so far.
One small but very important detail:
To handle subarrays that start right at index 0, we initialize the map with {0:1}, because the sum from index 0 to j itself might directly equal target.
By using this map, we can check and update the counts in O(1) while scanning the array once.
You can refer to the below article for understanding about how to find the number of subarrays with a particular sum in an array.
https://read.learnyard.com/dsa/subarray-sum-equals-k/
Approach
Step 1: Initialize the answer variable
Create a variable ans to store the total count of submatrices whose sum equals the target.
Initially set ans = 0.
Step 2: Create 2D row-wise prefixSum matrix and initialize
Construct a prefixSum matrix of the same size as the input matrix, initialized with zeros.
Each cell prefixSum[i][j] will store the sum of elements in row i from column 0 to column j.
Step 3: Loop to fill prefixSum row by row
Use an outer loop i from 0 to n - 1 (where n is the number of rows in the matrix).
Step 4: Loop through columns to compute row-wise prefix sum
For each row i, use a loop j from 0 to m - 1 (where m is the number of columns).
At each step, keep a running sum of elements from column 0 to column j.
Step 5: Populate the current cell of prefixSum
For each cell (i, j):
– If j > 0, then prefixSum[i][j] = prefixSum[i][j - 1] + matrix[i][j]
– Else, prefixSum[i][j] = matrix[i][j]
Step 6: Loop to fix the starting column of the submatrix
Use a loop start_col from 0 to m - 1 to choose the left edge of each submatrix.
Step 7: Loop to fix the ending column of the submatrix
For each start_col, use another loop end_col from start_col to m - 1 to choose the right edge.
Step 8: Initialize hashmap and running sum
For each fixed pair (start_col, end_col):
– Create an empty hashmap prefixCount to store counts of running sums.
– Initialize prefixCount[0] = 1 to account for subarrays that start from the first row.
– Initialize running_sum = 0.
Step 9: Loop through each row to build the running sum
Use a loop row from 0 to n - 1.
Step 10: Calculate the sum of the current row between start_col and end_col
For the current row:
– If start_col == 0, take prefixSum[row][end_col].
– Else, use prefixSum[row][end_col] - prefixSum[row][start_col - 1].
Step 11: Update running sum and count valid subarrays
– Add this current row sum to running_sum.
– Check if running_sum - target exists in prefixCount.
– If yes, increment ans by prefixCount[running_sum - target] (number of previous times this sum occurred).
Step 12: Update the hashmap with the current running_sum
Increase prefixCount[running_sum] by 1 to record that we’ve seen this sum now.
Step 13: Return ans as the required value
After scanning all rows and all column pairs, return ans as the final count of submatrices whose sum equals the target.
Dry Run
Let’s do a detailed dry run of the optimal approach (fixing column pairs and using running sum + hashmap)
for the input: matrix = [[1, -1], [-1, 1]], target = 0
We want to find the number of non-empty submatrices whose sum equals the target.
Step 1: Understand the matrix
Original matrix: first row has 1, -1; second row has -1, 1
Number of rows (n) = 2
Number of columns (m) = 2
Initialize ans = 0 → this will store the total count of valid submatrices.
Step 2: Build the row-wise prefixSum matrix
prefixSum[0][0] = matrix[0][0] = 1
prefixSum[0][1] = prefixSum[0][0] + matrix[0][1] = 1 + (-1) = 0
prefixSum[1][0] = matrix[1][0] = -1
prefixSum[1][1] = prefixSum[1][0] + matrix[1][1] = -1 + 1 = 0
Final prefixSum matrix:
– first row: 1, 0
– second row: -1, 0
Step 3: Fix starting and ending columns (start_col and end_col)
start_col = 0
end_col = 0 (we look at only the first column)
Initialize hashmap prefixCount = {0:1}
running_sum = 0
Loop through each row to compute row sums and update counts:
row = 0:
Since start_col=0: current_row_sum = prefixSum[0][0] = 1
running_sum += 1 → running_sum=1
Check if running_sum - target = 1 - 0 = 1 exists in prefixCount → no
Update prefixCount: prefixCount[1]=1
row = 1:
current_row_sum = prefixSum[1][0] = -1
running_sum += -1 → running_sum=0
Check if running_sum - target = 0 - 0 = 0 exists in prefixCount → yes, count=1
ans += 1 → ans=1
Update prefixCount: prefixCount[0]=2
end_col = 1 (consider first two columns)
Re-initialize prefixCount = {0:1}, running_sum=0
row = 0:
current_row_sum = prefixSum[0][1]=0
running_sum += 0 → running_sum=0
running_sum - target=0-0=0 exists in prefixCount → count=1
ans +=1 → ans=2
Update prefixCount: prefixCount[0]=2
row = 1:
current_row_sum = prefixSum[1][1]=0
running_sum+=0 → running_sum=0
running_sum - target=0 exists → count=2
ans+=2 → ans=4
Update prefixCount: prefixCount[0]=3
start_col =1
end_col=1 (only second column)
Re-initialize prefixCount={0:1}, running_sum=0
row=0:
Since start_col>0, current_row_sum=prefixSum[0][1]-prefixSum[0][0]=0-1=-1
running_sum+=-1 → running_sum=-1
running_sum - target = -1-0=-1 not in prefixCount
Update prefixCount: prefixCount[-1]=1
row=1:
current_row_sum=prefixSum[1][1]-prefixSum[1][0]=0-(-1)=1
running_sum+=1 → running_sum=0
running_sum - target=0 exists in prefixCount → count=1
ans+=1 → ans=5
Update prefixCount: prefixCount[0]=1
Final Result
Total number of non-empty submatrices that sum to target (0): ans=5
These 5 submatrices are:
– Rows 0–0, columns 0–1 (first row, both columns)
– Rows 0–1, columns 0–0 (first column, both rows)
– Rows 0–1, columns 0–1 (whole matrix)
– Rows 0–1, columns 1–1 (second column, both rows)
– Rows 1–1, columns 0–1 (second row, both columns)
Code for All Languages
C++
#include <iostream> // For input and output
#include <vector> // For using vector
#include <unordered_map> // For using hashmap
using namespace std;
class Solution {
public:
int numSubmatrixSumTarget(vector<vector<int>>& matrix, int target) {
int n = matrix.size(); // Number of rows
int m = matrix[0].size(); // Number of columns
// Step 1: Initialize the answer variable
int ans = 0;
// Step 2: Create row-wise prefixSum matrix and initialize
vector<vector<int>> prefixSum(n, vector<int>(m, 0));
// Step 3: Loop to fix the current row
for (int row = 0; row < n; row++) {
// Step 4: Loop through columns to compute row-wise prefix sum
int running_row_sum = 0;
for (int col = 0; col < m; col++) {
running_row_sum += matrix[row][col];
prefixSum[row][col] = running_row_sum;
}
}
// Step 5: Loop to fix the starting column start_col
for (int start_col = 0; start_col < m; start_col++) {
// Step 6: Loop to fix the ending column end_col
for (int end_col = start_col; end_col < m; end_col++) {
// Step 7: Initialize running_sum and prefixCount hashmap
unordered_map<int, int> prefixCount;
prefixCount[0] = 1; // To count submatrices starting from the first row
int running_sum = 0;
// Step 8: Loop through each row to calculate current_row_sum between start_col and end_col
for (int row = 0; row < n; row++) {
// Step 9: Get current_row_sum using prefixSum
int current_row_sum = prefixSum[row][end_col];
if (start_col > 0) {
current_row_sum -= prefixSum[row][start_col - 1];
}
// Step 10: Add current_row_sum to running_sum
running_sum += current_row_sum;
// Step 11: Check if running_sum - target exists in prefixCount
if (prefixCount.find(running_sum - target) != prefixCount.end()) {
ans += prefixCount[running_sum - target];
}
// Step 12: Update prefixCount hashmap with running_sum
prefixCount[running_sum]++;
}
}
}
// Step 13: Return ans as the required value
return ans;
}
};
int main() {
int n, m, target;
cin >> n >> m >> target; // Input number of rows, columns, and target
vector<vector<int>> matrix(n, vector<int>(m));
// Input the matrix elements
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
cin >> matrix[i][j];
}
}
Solution sol;
int result = sol.numSubmatrixSumTarget(matrix, target);
// Output the result
cout << result << endl;
return 0;
}
Java
import java.util.*; // For Scanner and HashMap
class Solution {
public int numSubmatrixSumTarget(int[][] matrix, int target) {
int n = matrix.length; // Number of rows
int m = matrix[0].length; // Number of columns
// Step 1: Initialize the answer variable
int ans = 0;
// Step 2: Create row-wise prefixSum matrix and initialize
int[][] prefixSum = new int[n][m];
// Step 3: Loop to fix the current row
for (int row = 0; row < n; row++) {
// Step 4: Loop through columns to compute row-wise prefix sum
int running_row_sum = 0;
for (int col = 0; col < m; col++) {
running_row_sum += matrix[row][col];
prefixSum[row][col] = running_row_sum;
}
}
// Step 5: Loop to fix the starting column start_col
for (int start_col = 0; start_col < m; start_col++) {
// Step 6: Loop to fix the ending column end_col
for (int end_col = start_col; end_col < m; end_col++) {
// Step 7: Initialize running_sum and prefixCount hashmap
Map<Integer, Integer> prefixCount = new HashMap<>();
prefixCount.put(0, 1);
int running_sum = 0;
// Step 8: Loop through each row to calculate current_row_sum between start_col and end_col
for (int row = 0; row < n; row++) {
// Step 9: Get current_row_sum using prefixSum
int current_row_sum = prefixSum[row][end_col];
if (start_col > 0) {
current_row_sum -= prefixSum[row][start_col - 1];
}
// Step 10: Add current_row_sum to running_sum
running_sum += current_row_sum;
// Step 11: Check if running_sum - target exists in prefixCount
ans += prefixCount.getOrDefault(running_sum - target, 0);
// Step 12: Update prefixCount hashmap with running_sum
prefixCount.put(running_sum, prefixCount.getOrDefault(running_sum, 0) + 1);
}
}
}
// Step 13: Return ans as the required value
return ans;
}
}
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
int m = sc.nextInt();
int target = sc.nextInt();
int[][] matrix = new int[n][m];
for (int i = 0; i < n; i++)
for (int j = 0; j < m; j++)
matrix[i][j] = sc.nextInt();
Solution sol = new Solution();
System.out.println(sol.numSubmatrixSumTarget(matrix, target));
}
}
Python
from typing import List
from collections import defaultdict
class Solution:
def numSubmatrixSumTarget(self, matrix: List[List[int]], target: int) -> int:
n = len(matrix) # Number of rows
m = len(matrix[0]) # Number of columns
# Step 1: Initialize the answer variable
ans = 0
# Step 2: Create row-wise prefixSum matrix and initialize
prefixSum = [[0] * m for _ in range(n)]
# Step 3: Loop to fix the current row
for row in range(n):
# Step 4: Loop through columns to compute row-wise prefix sum
running_row_sum = 0
for col in range(m):
running_row_sum += matrix[row][col]
prefixSum[row][col] = running_row_sum
# Step 5: Loop to fix the starting column start_col
for start_col in range(m):
# Step 6: Loop to fix the ending column end_col
for end_col in range(start_col, m):
# Step 7: Initialize running_sum and prefixCount hashmap
prefixCount = defaultdict(int)
prefixCount[0] = 1
running_sum = 0
# Step 8: Loop through each row to calculate current_row_sum
for row in range(n):
# Step 9: Get current_row_sum
current_row_sum = prefixSum[row][end_col]
if start_col > 0:
current_row_sum -= prefixSum[row][start_col - 1]
# Step 10: Add to running_sum
running_sum += current_row_sum
# Step 11: Check if running_sum - target in prefixCount
ans += prefixCount[running_sum - target]
# Step 12: Update prefixCount
prefixCount[running_sum] += 1
# Step 13: Return ans as the required value
return ans
if __name__ == "__main__":
n, m, target = map(int, input().split())
matrix = [list(map(int, input().split())) for _ in range(n)]
sol = Solution()
print(sol.numSubmatrixSumTarget(matrix, target))
Javascript
/**
* @param {number[][]} matrix
* @param {number} target
* @return {number}
*/
var numSubmatrixSumTarget = function(matrix, target) {
const n = matrix.length; // Number of rows
const m = matrix[0].length; // Number of columns
// Step 1: Initialize the answer variable
let ans = 0;
// Step 2: Create row-wise prefixSum matrix and initialize
const prefixSum = Array.from({ length: n }, () => Array(m).fill(0));
// Step 3: Loop to fix the current row
for (let row = 0; row < n; row++) {
// Step 4: Loop through columns to compute row-wise prefix sum
let running_row_sum = 0;
for (let col = 0; col < m; col++) {
running_row_sum += matrix[row][col];
prefixSum[row][col] = running_row_sum;
}
}
// Step 5: Loop to fix the starting column start_col
for (let start_col = 0; start_col < m; start_col++) {
// Step 6: Loop to fix the ending column end_col
for (let end_col = start_col; end_col < m; end_col++) {
// Step 7: Initialize running_sum and prefixCount hashmap
const prefixCount = new Map();
prefixCount.set(0, 1);
let running_sum = 0;
// Step 8: Loop through each row
for (let row = 0; row < n; row++) {
// Step 9: Get current_row_sum
let current_row_sum = prefixSum[row][end_col];
if (start_col > 0) {
current_row_sum -= prefixSum[row][start_col - 1];
}
// Step 10: Add to running_sum
running_sum += current_row_sum;
// Step 11: Check if running_sum - target exists
ans += prefixCount.get(running_sum - target) || 0;
// Step 12: Update prefixCount
prefixCount.set(running_sum, (prefixCount.get(running_sum) || 0) + 1);
}
}
}
// Step 13: Return ans as the required value
return ans;
};
// Driver code
const readline = require("readline");
const rl = readline.createInterface({ input: process.stdin, output: process.stdout });
let inputs = [], n, m, target;
rl.on("line", line => {
inputs.push(line.trim());
if (inputs.length === 1) {
[n, m, target] = inputs[0].split(' ').map(Number);
} else if (inputs.length === n + 1) {
const matrix = [];
for (let i = 1; i <= n; i++) {
matrix.push(inputs[i].split(' ').map(Number));
}
console.log(numSubmatrixSumTarget(matrix, target));
rl.close();
}
});
Time Complexity: O(m² * n)
Let us denote:
– n = number of rows in the matrix
– m = number of columns in the matrix
Building the Row-wise Prefix Sum Matrix: O(n * m)
We first preprocess the matrix to build a row-wise prefix sum for each row.
Each row takes O(m) time, and there are n rows.
Total time to build this prefixSum matrix is:
O(n * m)
Outer Loops for Fixing Columns: O(m²)
We fix the starting column index start_col, which runs from 0 to m − 1 (m choices).
For each start_col, we fix the ending column index end_col, which runs from start_col to m − 1 (up to m choices).
These two nested loops together run in:
O(m²) time.
Inner Loop for Rows and Subarray Sum: O(n)
For every fixed pair of columns (start_col, end_col):
– We loop through all rows from 0 to n − 1 to compute current_row_sum and maintain running_sum.
– At each row, we update the hashmap prefixCount and check if running_sum - target has been seen before.
All this work per fixed pair of columns takes:
O(n) time.
Total Time per Pair of Columns: O(n)
So, for each of the O(m²) pairs of columns, we spend O(n) time:
– Computing current_row_sum per row
– Updating running_sum and prefixCount hashmap
– Counting subarrays whose sum equals the target
Final Time Complexity: O(m² * n)
Putting it all together:
– O(m²) choices for the pair (start_col, end_col)
– For each such pair, O(n) time to process all rows
Total time complexity becomes: O(m²) × O(n) = O(m² * n)
Space Complexity: O(n * m)
We build an extra prefixSum matrix of the same dimensions as the input matrix, which uses O(n * m) additional space.
Detailed breakdown:
– Input space: the input matrix itself → O(n * m)
– Output space: the answer variable ans → O(1)
– Extra auxiliary space:
The prefixSum matrix → O(n * m)
Total Space Complexity: = O(n * m)
Learning Tip
Now we have successfully tackled this problem, let's try these similar problems.
You are given a 0-indexed m x n binary matrix grid. You can move from a cell (row, col) to any of the cells (row + 1, col) or (row, col + 1) that has the value 1. The matrix is disconnected if there is no path from (0, 0) to (m - 1, n - 1).
You can flip the value of at most one (possibly none) cell. You cannot flip the cells (0, 0) and (m - 1, n - 1).
Return true if it is possible to make the matrix disconnect or false otherwise.