Number of Flowers in Full Bloom Solution In C++/Java/Python/JS
Problem Description
You are given a 0-indexed 2D integer array flowers, where flowers[i] = [start i, end i] means the ith flower will be in full bloom from start i to end i (inclusive).
You are also given a 0-indexed integer array people of size n, where people[i] is the time that the ith person will arrive to see the flowers.
Return an integer array answer of size n, where answer[i] is the number of flowers that are in full bloom when the ith person arrives.
Example
Input: flowers = [[1,6],[3,7],[9,12],[4,13]], people = [2,3,7,11]
Output: [1,2,2,2]
Explanation: The figure above shows the times when the flowers are in full bloom and when the people arrive.
For each person, we return the number of flowers in full bloom during their arrival.
Input: flowers = [[1,10],[3,3]], people = [3,3,2]
Output: [2,2,1]
Explanation: The figure above shows the times when the flowers are in full bloom and when the people arrive.
For each person, we return the number of flowers in full bloom during their arrival.
Constraints
- 1 <= flowers.length <= 5 * 10^4
- flowers[i].length == 2
- 1 <= start i <= end i <= 10^9
- 1 <= people.length <= 5 * 10^4
- 1 <= people[i] <= 10^9
Can we imagine as a garden with flowers placed column wise, and everytime a person enters, he/she will note down the flowers in a particular column.
How can we simulate this process ? Let's figure it together.
Brute Force Approach
Intuition
Imagine we have a big field with lots of flowers, and each flower will be blooming from day X to day Y. These information will be given us in a flowers[][]. Where flowers[i][0] will represent the start day of bloom and flowers[i][1] will represent until when the flower will stop blooming.
Now, people come to the field on certain days, and they ask, “How many flowers are blooming today?”
So, Every time a person comes, we go to each flower one by one and check if the flower is blooming or not. If it blooms we will count it or else we will skip and move to the next. We do this for every single person that arrives to our field.
Ever wondered how can we code it up?
We can declare a vector/list of size 10^9(as given in constraints) to store the start day of bloom and end day of bloom of each flower. What ???
10^9 ?? Is it programmatically possible to declare an array of size 10^9 ?
No, this will result in Memory Limit Exceeded because a vector/list can only store upto 10^5 elements inside it !!
If , we were given comparatively lesser constraint size. We could follow a approach as mentioned below.
Approach
Step 1: Initialize an array/vector say garden[] with size given in constraints and ans[] to return the result.
Step 2: Iterate over the flowers[][]. Extract the start as flowers[i][0] and end as flowers[i][1].
Then run a loop from j=start to j<=end. Add +1 to garden[j] over each index until the iteration.
Step 3: Iterate over the people[] array and store the value of garden[i] to ans[i].
Step 4: Return the ans[].
Memory Limit Exceeded wasn't the only point of improvement. But imagine , if we have a long list of queries[][] , then we had to visit each column and 1 plant over time. Hectic!!
We have to figure out a optimized approach in terms of both space and time!!
Let's figure it out together.
Optimal Approach
Intuition
Imagining the same scenario, we were visiting to each flower , then checked if it is blooming or not. If it blooms we will count it and then tell it to the person. Imagine there are hundreds of people then we will end up moving the whole garden 100 times. We have to find a smarter way to figure out the number of flowers that bloom on a particular day.
Each flower in the garden tells us two things, one is on which day did they start blooming and when will they stop blooming. Can we make use of this information in a smarter way.
This means in flowers[][] array, flowers[i][0] represents when the flower starts blooming and flowers[i][1] represents the flower will stop blooming after this day.
This says a flower will bloom from start to end+1(exclusive).
We don’t need to keep track of every single day on the timeline. Instead, we focus only on important days: When a flower starts blooming (start day) and when a flower stops blooming (end + 1 day).
For example:
If a flower blooms from day 3 to day 6. At day 3, the number of blooming flowers increases by 1. At day 7 (end + 1), the number of blooming flowers decreases by 1.
Let's do one thing. Let's maintain a record where, we can just mention the day where a flower blooms. In other words we can enter a record with start -> 1 as a pair and end+1 -> -1 as another.
This entry means that on start day one flower is blooming and on end day+1 , one flower stopped blooming.
Now. let's record all such entries that are mentioned in the flowers[][].
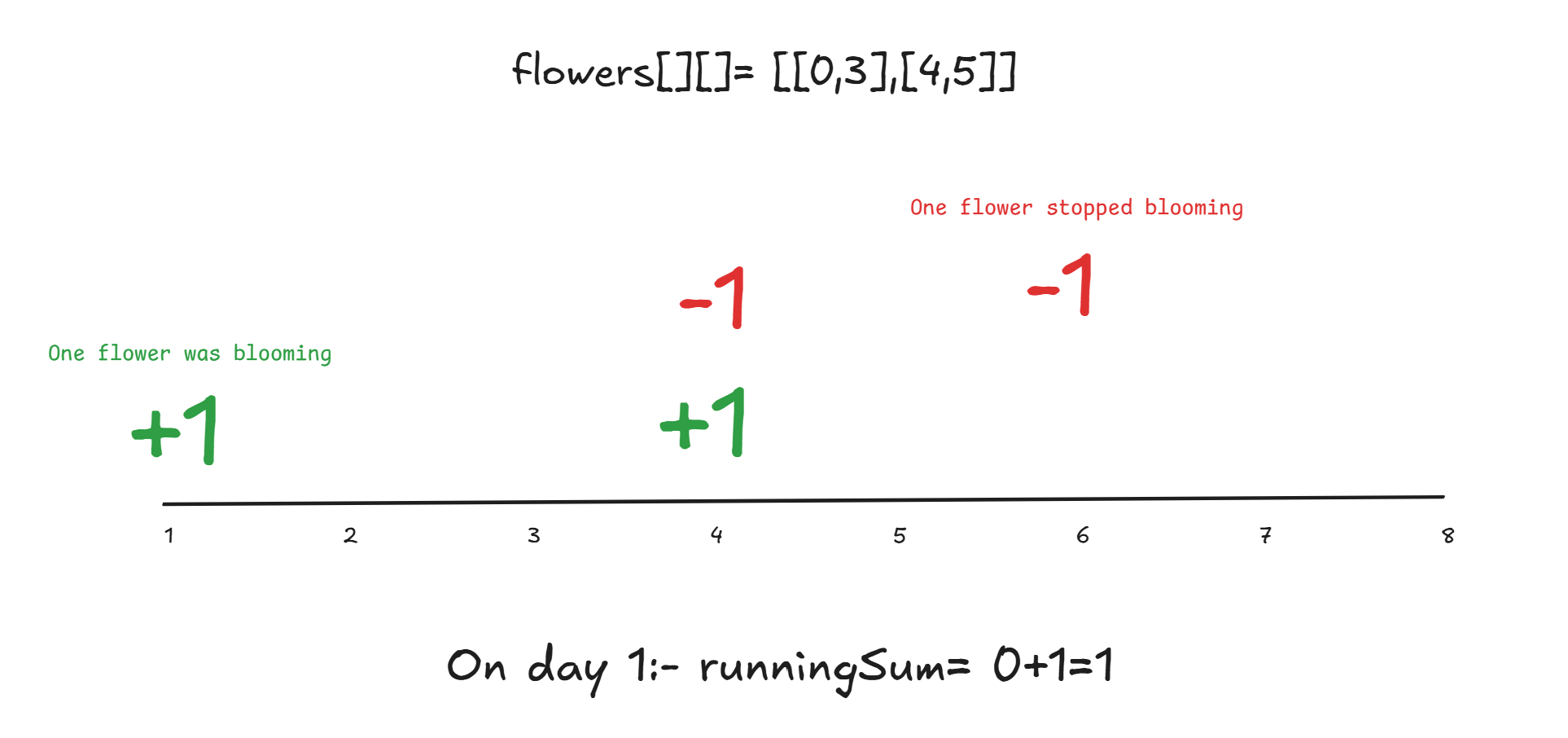
For example, we are given flowers[][]= [[0,3],[4,5]].
Our record will have 0->1 , 4->-1 again 4->1 so 4->0 and 6->-1.
Now, if a person asks us how many flowers bloom on 4th day. Shall we answer 0?
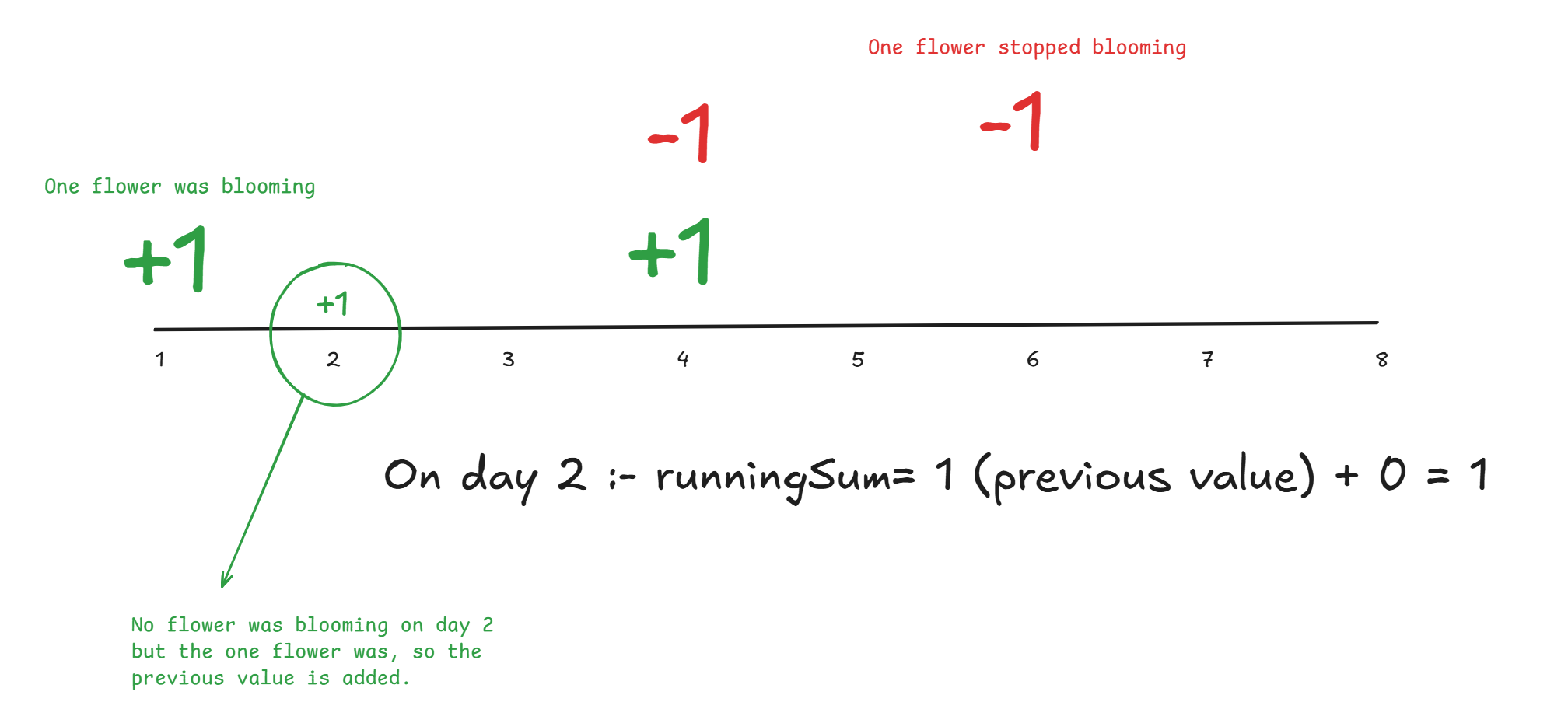
No, what we will do is maintain a runningSum with 0. As we go through our first entry which is 0 -> 1, we will add 1 (value mapped to 0).
Which means at day 1 there was 1 flower blooming , similarly when we encounter the entry 4, we will add the value mapped to 4 which is 0. The runningSum is 0+1=1, so we can say that there was 1 flower blooming on that particular day.
Yes !! We are right. We are using a runningSum which used the previous values which is nothing but
runningSum= runningSum + current value
So, since we maintained a running Sum to store the previous values ,so technically we are sweeping the previous values and bring them front and using it to answer the no of flowers that bloomed on that day.
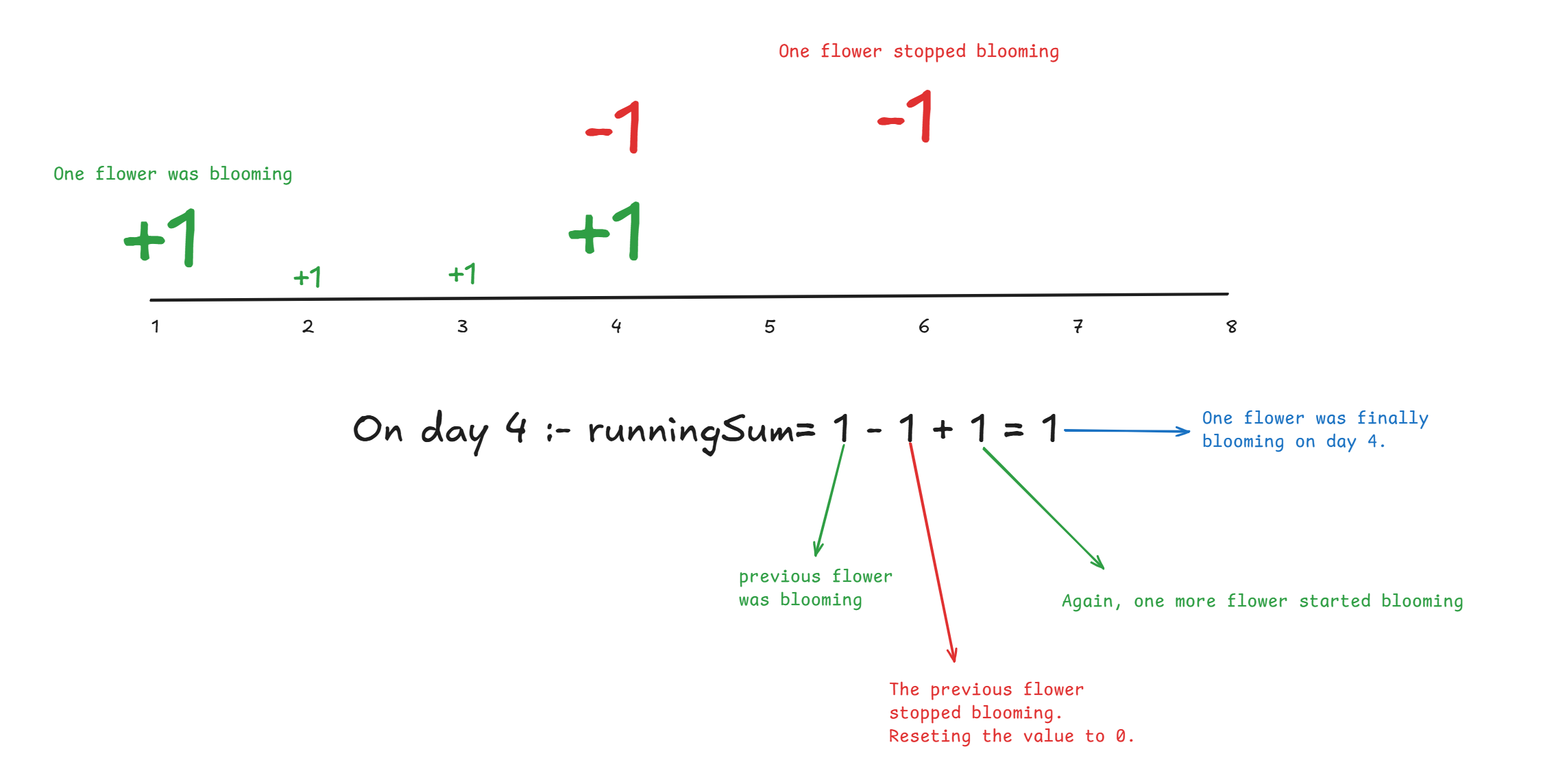
But, what was the purpose of marking -1 and how is it getting us the right answer?
Marking -1 , cancels out the previous value to 0 and we can start fresh again.
Refer the below image to understand it better !
Did you observed that we were iterating over our records ordered wise.
Why are we maintaining the record in sorted manner ?
The sorting of the entries in the record is crucial because we need to process the bloom start and end events in chronological order to calculate active blooms properly.
But programmatically , which data structure to use which stores the key-value pairs in a sorted fashion ?
Yes, it is called ordered_map in C++, TreeMap in Java and so on.
Now, since we have followed the above points and have entered values to a map, we will then sweep down the values from left to right and will be able to get the answer. This algorithm is nothing but the line sweep algorithm.
What is Line Sweep Algorithm ?
The Line Sweep Algorithm is a computational technique used to process intervals or events that occur over a continuous timeline or 2D space. It involves "sweeping" a vertical or horizontal line across the timeline or space, processing events in a specific order (usually sorted by time or position).
How it works ?
Identify Key Events: Each interval contributes two key events: a start (when the interval begins) and an end (when the interval ends). These events are marked with specific values (e.g., +1 for a start and -1 for an end).
Sweep Through Events
A line sweeps through the events, processing them sequentially. As the sweep progresses, a running total is updated based on the events.
During the sweep, you can calculate or track metrics such as the maximum overlap, total coverage, or active intervals.
Example Dry-Run:
You are given a list of intervals [(1,3),(2,5),(4,6)]. Count the maximum number of overlapping intervals at any point.
Dry Run:
Define Events:For each interval (start,end), create two events:
- (start,+1): An interval starts.
- (end,−1): An interval ends.
Events: [(1,+1),(3,−1),(2,+1),(5,−1),(4,+1),(6,−1)]
Sort Events:
- Sort by time. If times are equal, process ending events first (to handle overlapping properly).
- Sorted Events: [(1,+1),(2,+1),(3,−1),(4,+1),(5,−1),(6,−1)]
Process Events:
- Use a counter to track active intervals.
- Update the counter at each event and track the maximum.
Dry Run:Start with active = 0, max_overlap = 0.
Process events:
1. Event (1,+1): active = 1, max_overlap = 1.
2.Event (2,+1): active = 2, max_overlap = 2.
3.Event (3,−1): active = 1, max_overlap = 2.
4.Event (4,+1): active = 2, max_overlap = 2.
5.Event (5,−1): active = 1, max_overlap = 2.
6.Event (6,−1): active = 0, max_overlap = 2.
Result: The maximum overlap is 2.
Advantages of this algorithm
It is Efficient as it reduces the need for nested iterations or brute force, typically achieving a linear time complexity, where n is the number of events.
It works well in large data-sets.
Let's see how we can apply this logic into our code !!
Approach
Step 1: Initialize a map to store bloom counts for each time point. For each person's time in people[], set their initial bloom count in the map to 0.
Step 2: For each flower's blooming period:
- Increment the bloom count at the flower's start time.
- Decrement the bloom count at the flower's end time + 1.
Step 3: Initialize a variable total to track cumulative bloom counts.
Iterate through the map in sorted order:
- Add the current bloom count to total.
- Update the map's value at the current time point with total.
Step 4: Initialize an array ans of the same size as people[]. For each person's time in people[] : Set the corresponding element in ans to the bloom count stored in the map.
Step 5: Return the ans array.
Dry-Run
Flowers: [[1, 6], [2, 5], [4, 8], [7, 10]]
People: [3, 6, 8, 2]
Output: [2, 2, 2, 2]
Step 1: Initialize Map: Map initialized with people:
mp = {3: 0, 6: 0, 8: 0, 2: 0}
Step 2: Range Updates
For each flower's blooming period:
Flower [1, 6]: Start = 1, End = 6 + 1 = 7
Update mp = {3: 0, 6: 0, 8: 0, 2: 0, 1: 1, 7: -1}
Flower [2, 5]: Start = 2, End = 5 + 1 = 6
Update: mp = {3: 0, 6: -1, 8: 0, 2: 1, 1: 1, 7: -1}
Flower [4, 8]: Start = 4, End = 8 + 1 = 9
Update: mp = {3: 0, 6: -1, 8: 0, 2: 1, 1: 1, 7: -1, 4: 1, 9: -1}
Flower [7, 10]: Start = 7, End = 10 + 1 = 11
Update: mp = {3: 0, 6: -1, 8: 0, 2: 1, 1: 1, 7: 0, 4: 1, 9: -1, 11: -1}
Step 3: Prefix Sum
- Sort keys of the map: [1, 2, 3, 4, 6, 7, 8, 9, 11]
- Compute cumulative bloom counts:
Key = 1:
total = 1
mp = {1: 1, 2: 1, 3: 0, 4: 1, 6: -1, 7: 0, 8: 0, 9: -1, 11: -1}
Key = 2:
total = 2
mp = {1: 1, 2: 2, 3: 0, 4: 1, 6: -1, 7: 0, 8: 0, 9: -1, 11: -1}
Key = 3:
total = 2
mp = {1: 1, 2: 2, 3: 2, 4: 1, 6: -1, 7: 0, 8: 0, 9: -1, 11: -1}
Key = 4:
total = 3
mp = {1: 1, 2: 2, 3: 2, 4: 3, 6: -1, 7: 0, 8: 0, 9: -1, 11: -1}
Key = 6:
total = 2
mp = {1: 1, 2: 2, 3: 2, 4: 3, 6: 2, 7: 0, 8: 0, 9: -1, 11: -1}
Key = 7:
total = 2
mp = {1: 1, 2: 2, 3: 2, 4: 3, 6: 2, 7: 2, 8: 0, 9: -1, 11: -1}
Key = 8:
total = 2
mp = {1: 1, 2: 2, 3: 2, 4: 3, 6: 2, 7: 2, 8: 2, 9: -1, 11: -1}
Key = 9:
total = 1
mp = {1: 1, 2: 2, 3: 2, 4: 3, 6: 2, 7: 2, 8: 2, 9: 1, 11: -1}
Key = 11:
total = 0
mp = {1: 1, 2: 2, 3: 2, 4: 3, 6: 2, 7: 2, 8: 2, 9: 1, 11: 0}
Step 4: Generate Result
For each person in persons:
- 3 -> mp[3] = 2
- 6 -> mp[6] = 2
- 8 -> mp[8] = 2
- 2 -> mp[2] = 2
Final Output: [2, 2, 2, 2]
Optimal Code in all Languages
1. C++ Try on Compiler
class Solution {
public:
vector<int> fullBloomFlowers(vector<vector<int>>& flowers, vector<int>& persons) {
map<int,int> mp;
for(auto &x : persons)
mp[x] = 0;
// Formalising the Idea of Range Query Update in O(1) using the Map
for(auto &v : flowers){
int start = v[0], end = v[1]+1;
mp[start]++;
mp[end]--;
}
int total = 0;
// Generating the Prefix Sum
for(auto &p : mp){
total += p.second;
mp[p.first] = total;
}
int n = persons.size();
vector<int> ans(n);
// Generating the Resultant vector, by just taking the values from the map.
for(int i=0;i<n; i++){
ans[i] = mp[persons[i]];
}
return ans;
}
};2. Java Try on Compiler
class Solution {
public int[] fullBloomFlowers(int[][] flowers, int[] people) {
TreeMap<Integer, Integer> map = new TreeMap<>();
// Initialize the map with all persons' times and default bloom count as 0
for (int person : people) {
map.put(person, 0);
}
// Perform range updates in the map for flower blooming periods
for (int[] flower : flowers) {
int start = flower[0];
int end = flower[1] + 1;
map.put(start, map.getOrDefault(start, 0) + 1);
map.put(end, map.getOrDefault(end, 0) - 1);
}
// Generate prefix sums to calculate the bloom count at each time
int total = 0;
for (Map.Entry<Integer, Integer> entry : map.entrySet()) {
total += entry.getValue();
entry.setValue(total);
}
// Generate the resultant array by taking values from the map
int n = people.length;
int[] result = new int[n];
for (int i = 0; i < n; i++) {
result[i] = map.get(people[i]);
}
return result;
}
}
3. Python Try on Compiler
class Solution:
def fullBloomFlowers(self, flowers: List[List[int]], people: List[int]) -> List[int]:
# Initialize map with all people and default bloom count as 0
bloom_map = defaultdict(int)
for person in people:
bloom_map[person] = 0
# Perform range updates in the map for flower blooming periods
for start, end in flowers:
bloom_map[start] += 1
bloom_map[end + 1] -= 1
# Generate prefix sums to calculate the bloom count at each time
total = 0
for key in sorted(bloom_map.keys()):
total += bloom_map[key]
bloom_map[key] = total
# Generate the result array by taking values from the map
result = [bloom_map[person] for person in people]
return result4. JavaScript Try on Compiler
var fullBloomFlowers = function(flowers, people) {
const bloomMap = new Map();
// Initialize map with all people and default bloom count as 0
for (const person of people) {
bloomMap.set(person, 0);
}
// Perform range updates in the map for flower blooming periods
for (const [start, end] of flowers) {
bloomMap.set(start, (bloomMap.get(start) || 0) + 1);
bloomMap.set(end + 1, (bloomMap.get(end + 1) || 0) - 1);
}
// Generate prefix sums to calculate the bloom count at each time
let total = 0;
const sortedKeys = [...bloomMap.keys()].sort((a, b) => a - b);
for (const key of sortedKeys) {
total += bloomMap.get(key);
bloomMap.set(key, total);
}
// Generate the result array by taking values from the map
return people.map(person => bloomMap.get(person));
};Time Complexity: O(n*logk+k*logk+m*logk)
Initializing the map : Adding all people to the map takes O(m), where m is the size of the people[] array.
Processing flowers for range updates: For each flower, we perform two map operations which take O(logk), where k is the number of distinct keys in the map. With n flowers, this step takes O(nlogk).
Prefix sum calculation: Sorting the keys of the map takes O(klogk), where k is the number of unique keys in the map. Calculating the prefix sum involves iterating through all keys, which is O(k).
Result generation: For each person in people[], retrieving values from the map takes O(logk). This step takes O(mlogk).
Total Time Complexity:
O(m)+O(nlogk)+O(klogk)+O(mlogk)=O(nlogk+klogk+mlogk)
Space Complexity: O(k + m)
Auxiliary Space Complexity refers to the extra space required by an algorithm other than the input space.
Map: The map contains up to k unique keys, where k=m+2n(from persons and flower range updates).
Space: O(k).
Result array : Stores m values for the people[] array.
Space: O(m).
Total Auxiliary Space: O(k)+O(m)=O(k+m)
Total Space Complexity
Input space:
Flowers array: O(n).
People array: O(m).
Auxiliary space: O(k+m)
Overall Space Complexity: O(n+m) + O(k+m) = O(n+m+k)
Learning Tip
You are implementing a program to use as your calendar. We can add a new event if adding the event will not cause a double booking.
A double booking happens when two events have some non-empty intersection (i.e., some moment is common to both events.).
The event can be represented as a pair of integers startTime and endTime that represents a booking on the half-open interval [startTime, endTime), the range of real numbers x such that startTime <= x < endTime.
Implement the MyCalendar class:
- MyCalendar() Initializes the calendar object.
- boolean book(int startTime, int endTime) Returns true if the event can be added to the calendar successfully without causing a double booking. Otherwise, return false and do not add the event to the calendar.
A k-booking happens when k events have some non-empty intersection (i.e., there is some time that is common to all k events.)
You are given some events [startTime, endTime), after each given event, return an integer k representing the maximum k-booking between all the previous events.
Implement the MyCalendarThree class:
- MyCalendarThree() Initializes the object.
- int book(int startTime, int endTime) Returns an integer k representing the largest integer such that there exists a k-booking in the calendar.