Number of Atoms Solution In C++/Java/Python/JS
Problem
Given a string formula representing a chemical formula, return the count of each atom.
The atomic element always starts with an uppercase character, then zero or more lowercase letters, representing the name.
One or more digits representing that element's count may follow if the count is greater than 1. If the count is 1, no digits will follow.
For example, "H2O" and "H2O2" are possible, but "H1O2" is impossible.
Two formulas are concatenated together to produce another formula.
For example, "H2O2He3Mg4" is also a formula.
A formula placed in parentheses, and a count (optionally added) is also a formula.
For example, "(H2O2)" and "(H2O2)3" are formulas.
Return the count of all elements as a string in the following form: the first name (in sorted order), followed by its count (if that count is more than 1), followed by the second name (in sorted order), followed by its count (if that count is more than 1), and so on.
The test cases are generated so that all the values in the output fit in a 32-bit integer.
Example
Input: formula = "H2O"
Output: "H2O"
Explanation: The count of elements are {'H': 2, 'O': 1}.
Input: formula = "Mg(OH)2"
Output: "H2MgO2"
Explanation: The count of elements are {'H': 2, 'Mg': 1, 'O': 2}.
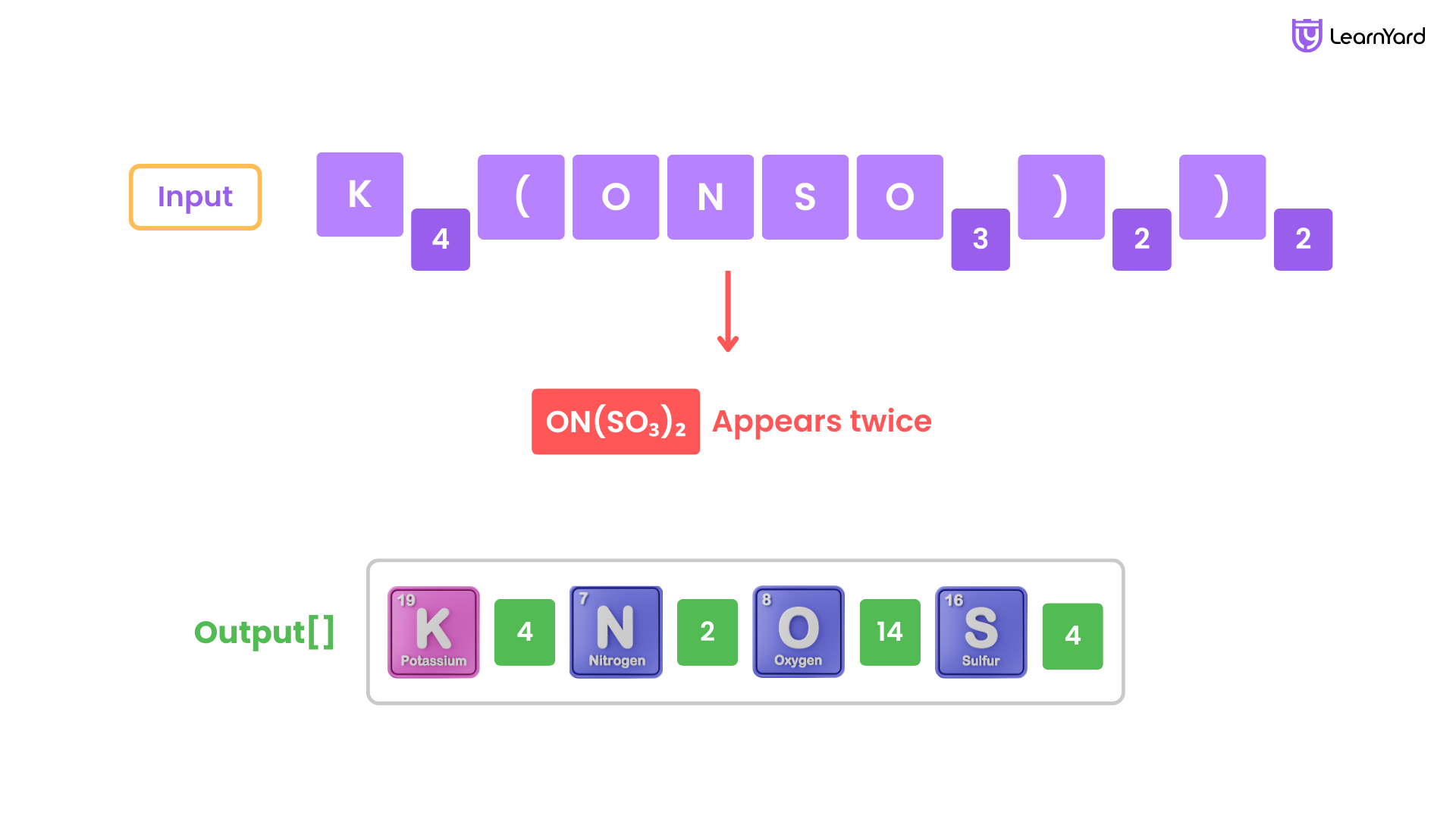
Input: formula = "K4(ON(SO3)2)2"
Output: "K4N2O14S4"
Explanation: The count of elements are {'K': 4, 'N': 2, 'O': 14, 'S': 4}.
Constraints
- 1 <= formula.length <= 1000
- formula consists of English letters, digits, '(', and ')'.
- formula is always valid.
The solution for "Number of Atoms" is an implementation-based question. We need to understand the flow of output using examples and then finalise the working algorithm.
Better Approach
Intuition
According to the given statement, we are given a string containing upper case letters, lower case letters, opening and closing parentheses, and integers in string format.
Suppose string formula = "Mg4(ON(SO3)2)2".
If we simplify the formula and try to gather how many atoms each element has, it comes to be
'Mg': 4, 'N': 2, 'O': 14, 'S': 4
When we try to get to the solution, the most naive approach is to start solving from the inner-most formula.

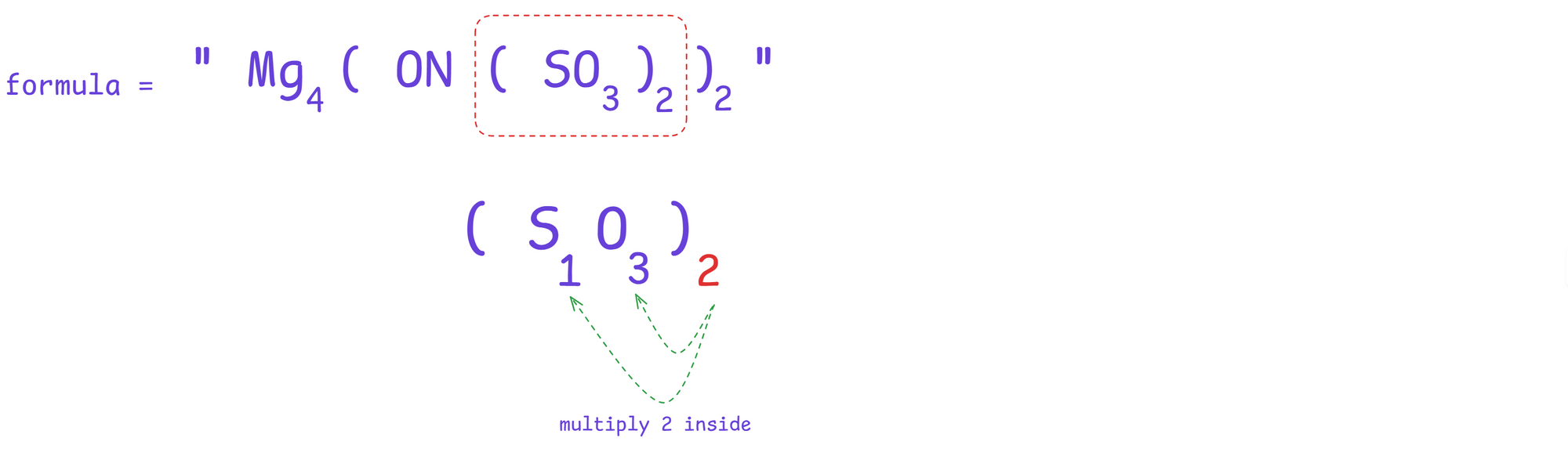
After multiplying the outer integer to the elements inside the inner brackets we get.

Similarly, we will proceed until we are left with no pair of parentheses.
But, how to simulate the process? How shall we iterate the whole string and come to a conclusion?
There are a few observations to notice, let's note down them first !!
1. An element starts with Upper Case followed by 0 or more Lower Case characters and then followed by an Integer.
2. If an element is enclosed inside a pair of parentheses and followed by an integer we have to multiply the integer with each of the atoms in the parentheses.
Example:- (SO2)2 -> S2O4
So, if formula = "Mg4", it signifies 4 atoms of Mg i.e. {Mg:4}.
So, let's do one thing let's keep a record of Atoms encountered along with their count.
In the above dry-run did you observe that the elements enclosed inside the parentheses were multiplied by the integer which was present outside the parentheses.
So, for this purpose the record we want must have a functionality that help us multiply the current integer with the most recent elements.
Most recent to be used first !!
It's a stack we are going to use. Now the question what to store inside the stack.
We will store a pair inside the stack. The pair contains the element name along with the number of atoms in it.

When we encounter a '(', we push it to the stack as well.

The simulation get's on going until we reach a ')' . Once we encounter a ')' we will pick up the integer next to it and multiply the values inside the stack.
We will multiply the integer until we get the ')'. The new pairs will again be pushed back to the stack.
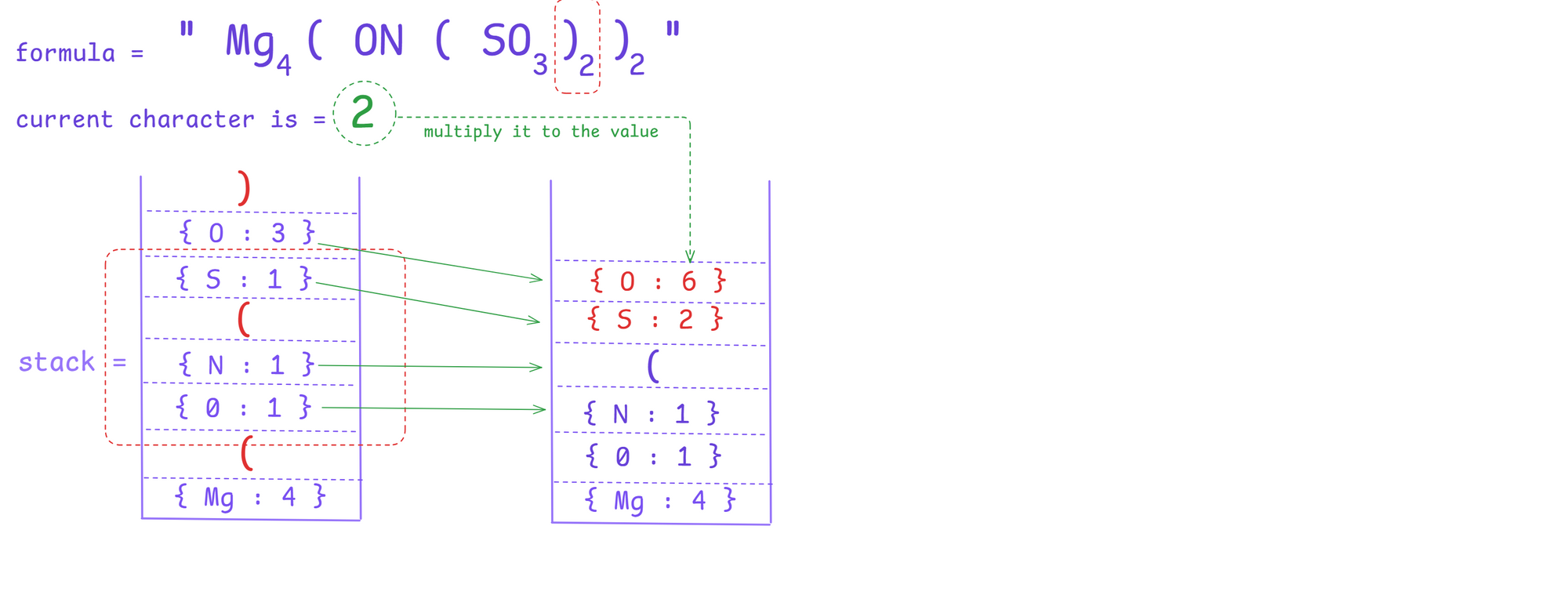
At last, when we follow the above steps, we will be getting the answer correctly.
Let's now see the algorithm!!
Number of Atoms Algorithm
We read uppercase letters to identify element symbols.
If lowercase letters follow, we append them to form the full element name.
We then extract the count (if present), defaulting to 1 if absent.
When we encounter '(', we push a marker ("(", -1) onto the stack.
When we encounter ')', we extract the multiplier (if any) and apply it to all
elements within the parentheses before pushing them back onto the stack.
We use a ordered map to store and maintain elements in lexicographical order.
We then construct the final output by appending each element name, followed by its count (if greater than 1).
We use a helper class to store element names and their counts within the stack.
Approach
Step 1: Initialize Data Structures
Create a stack to store element names and their counts.
Initialize index variables i, j, k for traversal.
Step 2: Iterate Through the Formula
If an uppercase letter is found:
- Start forming an element name.
- Append any following lowercase letters to complete the element name.
- Extract the count (if present), defaulting to 1 if absent.
- Push (element, count) to the stack.
If a '(' (opening parenthesis) is found:
- Push ("(", -1) onto the stack as a marker.
If a ')' (closing parenthesis) is found:
- Extract the count following ) (if present), defaulting to 1.
- Pop elements from the stack and multiply their counts by this value until "(" is found.
- Remove "(" from the stack.
- Push back the multiplied elements in the correct order.
Step 3: Aggregate Element Counts
- Use an ordered map(which sorts keys alphabetically) to store the final count of each element.
- Pop elements from the stack and update the count in the map.
Step 4: Build the Output String
- Traverse the sorted map.
- Append each element name followed by its count (only if greater than 1).
- Return the final formatted string.
number-of-atoms-better-approach-animation
Dry-Run
Inputformula ="Ca(OH)2Mg(OH)2"
Output"CaH4MgO4"
Step 1: Initialization
- Stack: [] (Empty)
- Index i starts at 0
- Map for element count: {} (Empty)
Step 2: Processing Ca
- C is an uppercase letter, so we start forming an element name.
- The next character a is lowercase, so the full element is "Ca".
- No digits follow, so the count is 1.
- Push ("Ca", 1) to the stack.
- Stack: [("Ca", 1)]
Step 3: Processing (
- ( is encountered, so push ("(", -1) as a marker.
- Stack: [("Ca", 1), ("(", -1)]
Step 4: Processing OH
- O is an uppercase letter.
- No lowercase letters follow, so the element is "O".
- No digits follow, so the count is 1.
- Push ("O", 1) to the stack.
- Stack: [("Ca", 1), ("(", -1), ("O", 1)]
- H is an uppercase letter.
- No lowercase letters follow, so the element is "H".
- No digits follow, so the count is 1.
- Push ("H", 1) to the stack.
- Stack: [("Ca", 1), ("(", -1), ("O", 1), ("H", 1)]
Step 5: Processing )2
- ) is encountered.
- The following number is 2, meaning everything inside the parentheses should be multiplied by 2.
- Pop elements from the stack until ( is found:
- Pop ("H", 1), multiply by 2, store as ("H", 2).
- Pop ("O", 1), multiply by 2, store as ("O", 2).
- Pop ("(", -1), discard.
- Push back ("O", 2) and ("H", 2).
- Stack: [("Ca", 1), ("O", 2), ("H", 2)]
Step 6: Processing Mg
- M is an uppercase letter.
- g is lowercase, so the full element is "Mg".
- No digits follow, so the count is 1.
- Push ("Mg", 1) to the stack.
- Stack: [("Ca", 1), ("O", 2), ("H", 2), ("Mg", 1)]
Step 7: Processing (
- ( is encountered, so push ("(", -1) as a marker.
- Stack: [("Ca", 1), ("O", 2), ("H", 2), ("Mg", 1), ("(", -1)]
Step 8: Processing OH
- O is an uppercase letter.
- No lowercase letters follow, so the element is "O".
- No digits follow, so the count is 1.
- Push ("O", 1) to the stack.
- Stack: [("Ca", 1), ("O", 2), ("H", 2), ("Mg", 1), ("(", -1), ("O", 1)]
- H is an uppercase letter.
- No lowercase letters follow, so the element is "H".
- No digits follow, so the count is 1.
- Push ("H", 1) to the stack.
- Stack: [("Ca", 1), ("O", 2), ("H", 2), ("Mg", 1), ("(", -1), ("O", 1), ("H", 1)]
Step 9: Processing )2
- ) is encountered.
- The following number is 2, meaning everything inside the parentheses should be multiplied by 2.
- Pop elements from the stack until ( is found:
- Pop ("H", 1), multiply by 2, store as ("H", 2).
- Pop ("O", 1), multiply by 2, store as ("O", 2).
- Pop ("(", -1), discard.
- Push back ("O", 2) and ("H", 2).
- Stack: [("Ca", 1), ("O", 2), ("H", 2), ("Mg", 1), ("O", 2), ("H", 2)]
Step 10: Compute Final Counts
Now, pop all elements from the stack and store in a sorted map:
Sorting by element name and formatting gives:
Output: "CaH4MgO4"
Number of Atoms solution
Now, let's checkout the Number of Atoms solution in c++, Java, Python and JavaScript
"Number of Atoms" Code in all Languages.
1. Number of Atoms solution in C++ Try on Compiler
#include <iostream>
#include <stack>
#include <map>
#include <vector>
#include <algorithm>
using namespace std;
// Function to parse atom counts
string countOfAtoms(string formula) {
stack<pair<string, int>> st;
int i = 0;
while (i < formula.size()) {
// If uppercase, start of element
if (isupper(formula[i])) {
string atom;
atom += formula[i++];
while (i < formula.size() && islower(formula[i])) {
atom += formula[i++];
}
int num = 0;
while (i < formula.size() && isdigit(formula[i])) {
num = num * 10 + (formula[i++] - '0');
}
if (num == 0) num = 1;
st.push({atom, num});
}
// If open bracket
else if (formula[i] == '(') {
st.push({"(", -1});
i++;
}
// If close bracket
else if (formula[i] == ')') {
i++;
int num = 0;
while (i < formula.size() && isdigit(formula[i])) {
num = num * 10 + (formula[i++] - '0');
}
if (num == 0) num = 1;
vector<pair<string, int>> temp;
while (st.top().first != "(") {
auto top = st.top(); st.pop();
temp.push_back({top.first, top.second * num});
}
st.pop();
reverse(temp.begin(), temp.end());
for (auto &p : temp) st.push(p);
}
}
map<string, int> mp;
while (!st.empty()) {
auto [key, val] = st.top(); st.pop();
mp[key] += val;
}
string res;
for (auto &[key, val] : mp) {
res += key;
if (val != 1) res += to_string(val);
}
return res;
}
int main() {
string formula;
cin >> formula;
cout << countOfAtoms(formula) << endl;
return 0;
}
2. Number of Atoms solution in Java Try on Compiler
import java.util.*;
public class Solution {
public String countOfAtoms(String formula) {
// Stack to hold elements and their counts
Stack<Pair<String, Integer>> stack = new Stack<>();
int i, j, k;
// Iterate over formula
for (i = 0; i < formula.length(); i++) {
char c = formula.charAt(i);
// If uppercase, start of element
if (Character.isUpperCase(c)) {
StringBuilder element = new StringBuilder();
element.append(c);
for (j = i + 1; j < formula.length(); j++) {
c = formula.charAt(j);
if (!Character.isLowerCase(c)) break;
element.append(c);
}
StringBuilder sdigit = new StringBuilder();
for (k = j; k < formula.length(); k++) {
c = formula.charAt(k);
if (!Character.isDigit(c)) break;
sdigit.append(c);
}
int digit = sdigit.length() == 0 ? 1 : Integer.parseInt(sdigit.toString());
stack.push(new Pair<>(element.toString(), digit));
i = k - 1;
}
// Handle opening parenthesis
else if (c == '(') {
stack.push(new Pair<>("(", -1));
}
// Handle closing parenthesis
else if (c == ')') {
StringBuilder sdigit = new StringBuilder();
for (j = i + 1; j < formula.length(); j++) {
c = formula.charAt(j);
if (!Character.isDigit(c)) break;
sdigit.append(c);
}
int digit = sdigit.length() == 0 ? 1 : Integer.parseInt(sdigit.toString());
List<Pair<String, Integer>> temp = new ArrayList<>();
Pair<String, Integer> op = new Pair<>("(", -1);
while (!stack.peek().equals(op)) {
Pair<String, Integer> p = stack.pop();
temp.add(new Pair<>(p.getKey(), p.getValue() * digit));
}
stack.pop();
Collections.reverse(temp);
for (Pair<String, Integer> p : temp) {
stack.push(p);
}
i = j - 1;
}
}
// Count all elements
Map<String, Integer> map = new TreeMap<>();
while (!stack.isEmpty()) {
Pair<String, Integer> p = stack.pop();
map.put(p.getKey(), map.getOrDefault(p.getKey(), 0) + p.getValue());
}
StringBuilder ans = new StringBuilder();
for (Map.Entry<String, Integer> entry : map.entrySet()) {
ans.append(entry.getKey());
if (entry.getValue() != 1) ans.append(entry.getValue());
}
return ans.toString();
}
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
String formula = scanner.nextLine();
Solution solution = new Solution();
System.out.println(solution.countOfAtoms(formula));
}
static class Pair<K, V> {
private final K key;
private final V value;
public Pair(K key, V value) {
this.key = key;
this.value = value;
}
public K getKey() { return key; }
public V getValue() { return value; }
public boolean equals(Object o) {
if (this == o) return true;
if (o == null || getClass() != o.getClass()) return false;
Pair<?, ?> pair = (Pair<?, ?>) o;
return Objects.equals(key, pair.key) && Objects.equals(value, pair.value);
}
public int hashCode() {
return Objects.hash(key, value);
}
}
}
3. Number of Atoms solution in Python Try on Compiler
from collections import defaultdict
def countOfAtoms(formula: str) -> str:
stack = []
i = 0
n = len(formula)
while i < n:
# Start of an atom
if formula[i].isupper():
atom = formula[i]
i += 1
while i < n and formula[i].islower():
atom += formula[i]
i += 1
num = 0
while i < n and formula[i].isdigit():
num = num * 10 + int(formula[i])
i += 1
num = num if num != 0 else 1
stack.append((atom, num))
# Open parenthesis
elif formula[i] == '(':
stack.append(('(', -1))
i += 1
# Close parenthesis
elif formula[i] == ')':
i += 1
num = 0
while i < n and formula[i].isdigit():
num = num * 10 + int(formula[i])
i += 1
num = num if num != 0 else 1
temp = []
while stack[-1][0] != '(':
atom, count = stack.pop()
temp.append((atom, count * num))
stack.pop()
for item in reversed(temp):
stack.append(item)
# Combine counts
counter = defaultdict(int)
for atom, count in stack:
counter[atom] += count
result = ''
for atom in sorted(counter):
result += atom + (str(counter[atom]) if counter[atom] > 1 else '')
return result
if __name__ == "__main__":
formula = input()
print(countOfAtoms(formula))
4. Number of Atoms solution in JavaScript Try on Compiler
function countOfAtoms(formula) {
const stack = [];
let i = 0;
while (i < formula.length) {
// Element
if (/[A-Z]/.test(formula[i])) {
let atom = formula[i++];
while (i < formula.length && /[a-z]/.test(formula[i])) {
atom += formula[i++];
}
let num = '';
while (i < formula.length && /\d/.test(formula[i])) {
num += formula[i++];
}
stack.push([atom, parseInt(num) || 1]);
}
// Open parenthesis
else if (formula[i] === '(') {
stack.push(['(', -1]);
i++;
}
// Close parenthesis
else if (formula[i] === ')') {
i++;
let num = '';
while (i < formula.length && /\d/.test(formula[i])) {
num += formula[i++];
}
let multiplier = parseInt(num) || 1;
let temp = [];
while (stack[stack.length - 1][0] !== '(') {
let [atom, count] = stack.pop();
temp.push([atom, count * multiplier]);
}
stack.pop(); // remove '('
for (let item of temp.reverse()) {
stack.push(item);
}
}
}
const map = new Map();
while (stack.length) {
let [atom, count] = stack.pop();
map.set(atom, (map.get(atom) || 0) + count);
}
const result = Array.from(map.entries())
.sort((a, b) => a[0].localeCompare(b[0]))
.map(([atom, count]) => atom + (count === 1 ? '' : count))
.join('');
return result;
}
// Read input from stdin using readline
const readline = require('readline');
const rl = readline.createInterface({
input: process.stdin,
output: process.stdout
});
rl.on('line', function (line) {
console.log(countOfAtoms(line));
rl.close();
});
Complexity Analysis of the problem
Time Complexity: O(n log m)
Parsing the Formula (O(n))
- We iterate through the formula once (for loop from i = 0 to formula.length()).
- Inside the loop, we extract atoms and their counts, which involves scanning a few extra characters (j and k loops).
- Each character in the formula is processed at most once, leading to an O(n) complexity.
Handling Parentheses (O(n))
- When encountering a ), we pop elements from the stack and update their counts.
- Since each element is pushed and popped at most once, the total work done is O(n).
Sorting the Atom Count Map (O(m log m))
- The atoms are stored in a TreeMap, which keeps them sorted.
- With m unique atoms, inserting each one into the map takes O(log m), resulting in a total O(m log m) complexity.
Building the Output String (O(m))
- The result string is constructed by iterating over m unique atoms in sorted order.
Overall Time Complexity:
O(n)+O(n)+O(m*logm)+O(m)=O(n+m*logm)
Since m (unique atoms) is generally much smaller than n (length of formula), the dominant term is O(n log m).
Space Complexity: O(n)
Auxiliary Space Complexity refers to the extra space required by an algorithm other than the input space.
Stack Storage (O(n)): In the worst case (e.g., "((((H2)2)2)2)"), the stack stores up to O(n) elements.
Temporary List for Parentheses Processing (O(n)): When handling ), we create a temporary list to hold elements popped from the stack.
TreeMap for Atom Count (O(m)): The TreeMap stores at most m unique atoms with their counts.
StringBuilders for Atoms and Counts (O(1)): These are used temporarily but do not contribute significantly to space complexity.
Total Auxiliary Space Complexity:
O(n)+O(n)+O(m)=O(n)
Total Space Complexity (Including Input Storage)
Input formula (O(n)): The formula itself is stored in memory.
Stack (O(n)): In the worst case, the stack stores all elements.
TreeMap (O(m)): Stores the final atom counts.
Temporary variables and result string (O(m)): The result string is of size O(m), where m is the number of unique atoms.
Total Space Complexity: O(n+m)
Since m is much smaller than n, the space complexity is O(n).
The algorithm we figured out was O(n^2) which might be slow if the constraints were higher. We as trainees of LearnYard must know the best approach. Let's observe few things and finalise the most optimized approach !!
Optimal Approach
Intuition
If we observe the same example that we took in the previous approach i.e. if string formula = "Mg4(ON(SO3)2)2".
In the previous approach we were waiting for an integer to come and then we traversed the stack and modified it.
What if we could know the multiplicity of the nested formula in the beginning itself?
Then we can apply the multiplicity to the atoms as we parse them. This will eliminate the need to revisit the atoms in the nested formula.
For example if formula = "Mg(OH)2". We are sure that the no of atoms of Mg will be 1 only and the 2 gets multiplied to O and H making the frequency of O:2 and H:2.
If we are aware of the rules that the formula follows, we must have realised that the integer will surely come after an element and not before an element.
If we first want to recognise that integer, we will start our iteration from the end of the string. Simple!!
So, if we look at the example formula = "Mg4(ON(SO3)2)2", The contribution of any integer on any atom will be :-

With the above image we come to know that
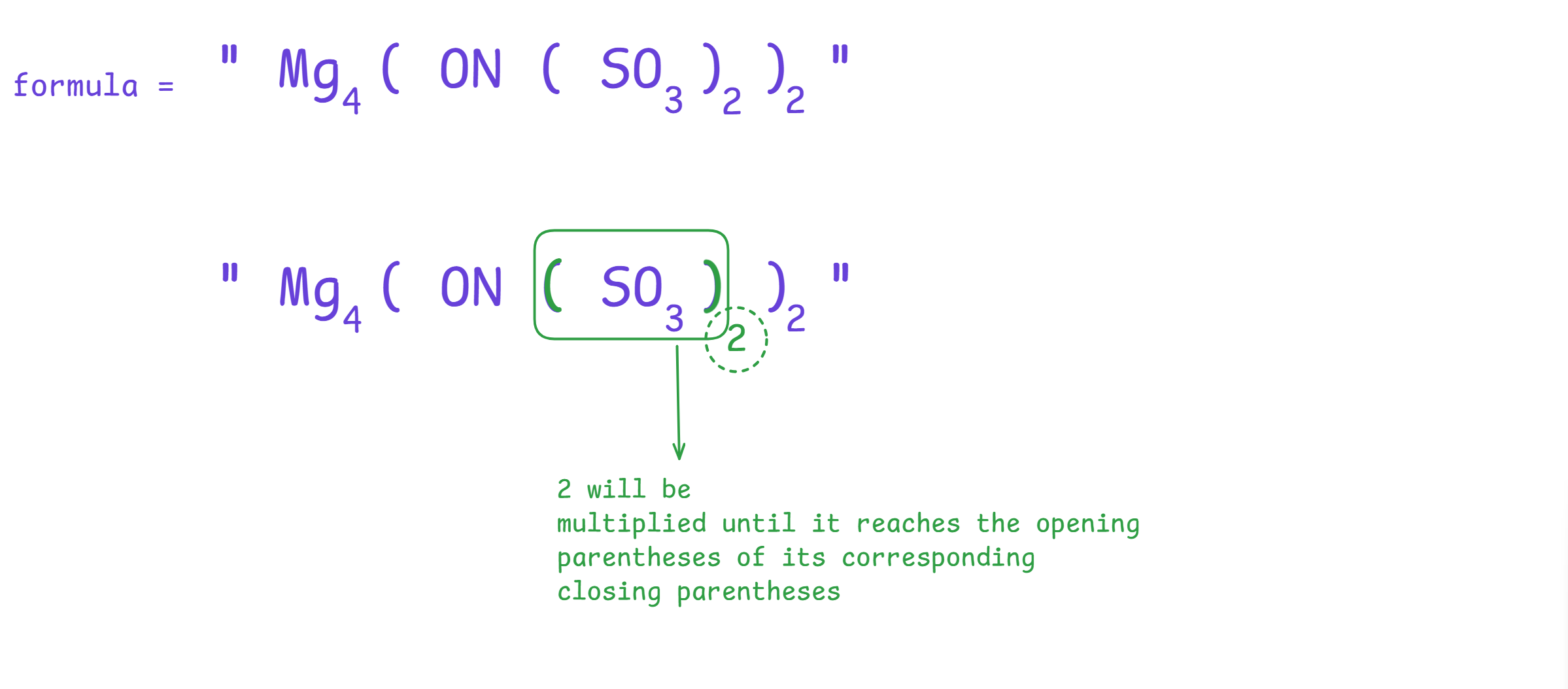
and,
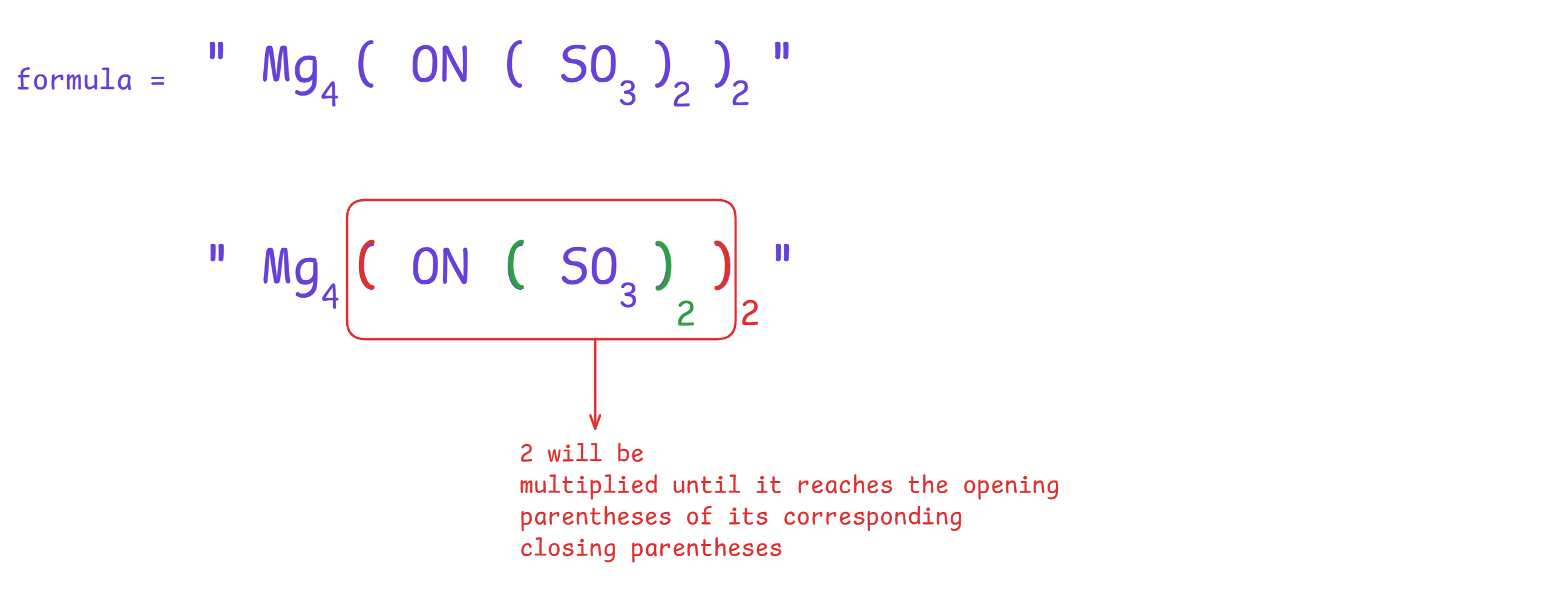
So, we can understand that we are going to pre-process something.
Something ?? Yes, we will pre-process the multiplication factor of each atom present in the formula.

Once, we pre-process the multiplication factor of each atom by traversing from right to left. Then, we can start iterating from left to right by just multiplying the atom with it's corresponding pre-processed multiplication factor.
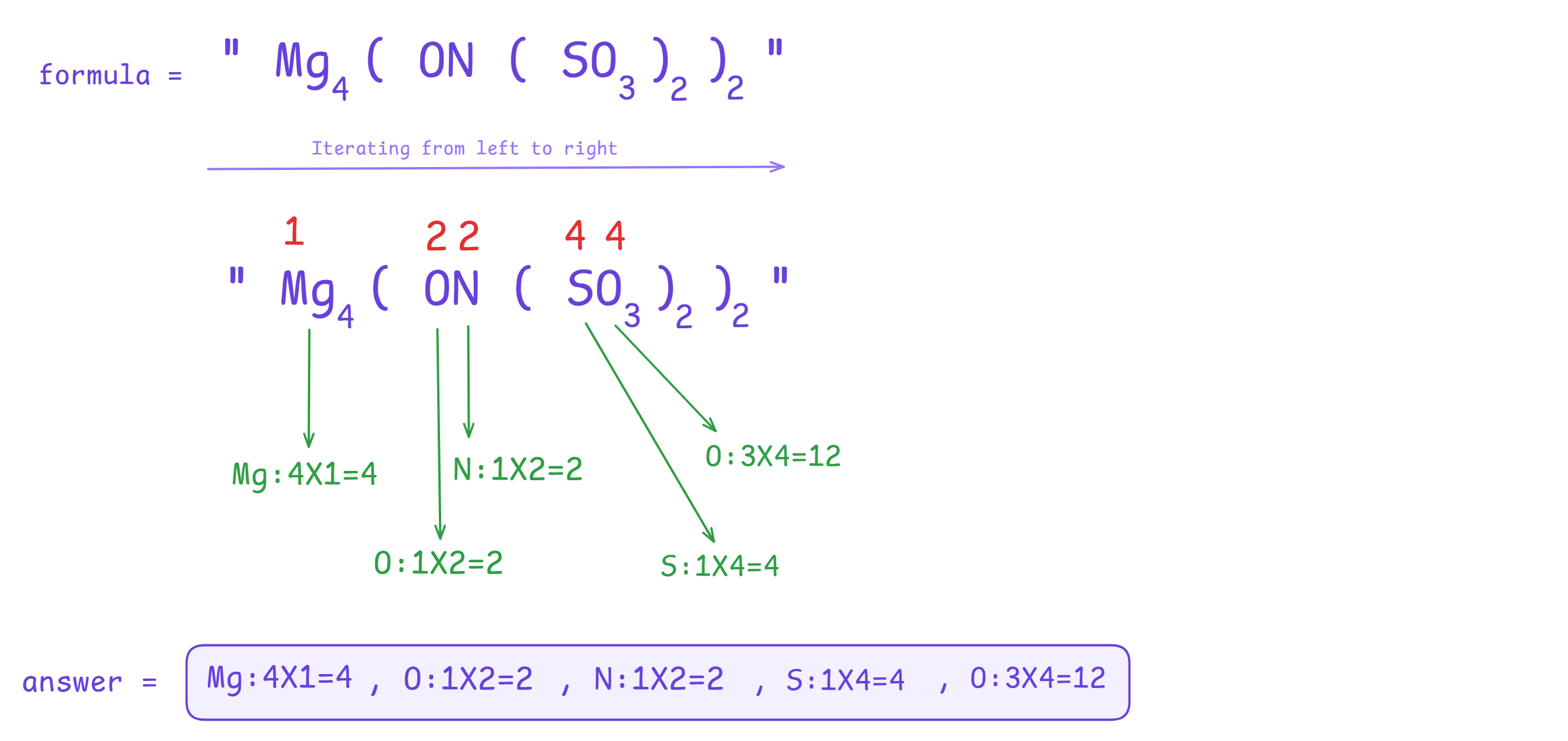
Let's now discuss the algorithm!!
Number of Atoms Algorithm
We process the chemical formula by scanning it from right to left, keeping track of multipliers to handle nested parentheses while maintaining a record of atom counts.
We use a stack to manage these multipliers, ensuring that counts are correctly distributed when parentheses are involved. As we move through the formula, we build atom names along with their counts, assuming a default count of one if none is specified.
When we encounter a closing parenthesis, we determine the multiplier that applies to the enclosed atoms and update their total counts accordingly. Upon reaching an opening parenthesis, we remove the last applied multiplier since the enclosed group has been fully processed.
Once all atom counts are extracted, we sort them alphabetically and format the final output, appending counts only when they are greater than one.
Let's now see how to code it up !!
Approach
Initialize Variables:
- Set runningMultiplier to 1. This will store the effective multiplier for atoms as we scan the formula.
- Create a multiplierStack to manage multipliers, initializing it with 1. The product of values in this stack represents the active multiplier, which is also stored in runningMultiplier.
- Use a HashMap called atomCountMap to store the count of each atom.
- Define two string builders: currentAtom for storing the name of the atom and currentCount for storing its count.
Traverse the Formula from Right to Left:
- If the current character is a digit, prepend it to currentCount to build multi-digit numbers.
- If it is a lowercase letter, prepend it to currentAtom as part of an atom’s name.
- If it is an uppercase letter, prepend it to currentAtom, completing the atom’s name.
- Retrieve the atom's count:
If currentCount is not empty, convert it to an integer and multiply by runningMultiplier.
Otherwise, use runningMultiplier as the default count. - Update atomCountMap with the new count for currentAtom.
- Reset currentAtom and currentCount for the next atom.
Handling Parentheses:
- If the character is a closing parenthesis ), interpret currentCount (if present) as currentMultiplier. If currentCount is empty, set currentMultiplier to 1.
- Push currentMultiplier onto multiplierStack and multiply runningMultiplier by currentMultiplier.
- Reset currentCount after processing the multiplier.
- If the character is an opening parenthesis (, remove the last multiplier from multiplierStack and adjust runningMultiplier accordingly by dividing it.
Sorting and Formatting the Output:
- Sort atomCountMap alphabetically by atom name.
- Construct the result string formattedFormula by iterating through the sorted map.
- Append each atom’s name to formattedFormula. If the atom count is greater than 1, append the count as well.
Return the Final Output: Return the formatted chemical formula as a string.
For better understanding , let us watch this video,
number-of-atoms-optimal-approach-animation
Dry-Run
Inputformula ="Ca(OH)2Mg(OH)2"
Output"CaH4MgO4"
Input: formula = "Ca(OH)2Mg(OH)2"
Expected Output: "CaH4MgO4"
Initialization
- runningMultiplier = 1
- multiplierStack = [1]
- atomCountMap = {}
Traversing Right to Left
We start scanning from the last character (index = formula.length() - 1).
Step 1: Processing 2
- currentCount = "2"
Step 2: Processing )
- currentMultiplier = 2 (from currentCount)
- Push 2 to multiplierStack → [1, 2]
- Update runningMultiplier = 1 * 2 = 2
- Reset currentCount
Step 3: Processing H
- currentAtom = "H"
- Count = 1
- atomCountMap["H"] = 1 * 2 = 2
- Reset currentAtom
Step 4: Processing O
- currentAtom = "O"
- Count = 1
- atomCountMap["O"] = 1 * 2 = 2
- Reset currentAtom
Step 5: Processing (
- Remove last multiplier from multiplierStack → [1]
- Update runningMultiplier = 2 / 2 = 1
Step 6: Processing g
- currentAtom = "g"
Step 7: Processing M
- currentAtom = "Mg"
- Count = 1
- atomCountMap["Mg"] = 1
- Reset currentAtom
Step 8: Processing 2
- currentCount = "2"
Step 9: Processing )
- currentMultiplier = 2 (from currentCount)
- Push 2 to multiplierStack → [1, 2]
- Update runningMultiplier = 1 * 2 = 2
- Reset currentCount
Step 10: Processing H
- currentAtom = "H"
- Count = 1
- atomCountMap["H"] = 2 + (1 * 2) = 4
- Reset currentAtom
Step 11: Processing O
- currentAtom = "O"
- Count = 1
- atomCountMap["O"] = 2 + (1 * 2) = 4
- Reset currentAtom
Step 12: Processing (
- Remove last multiplier from multiplierStack → [1]
- Update runningMultiplier = 2 / 2 = 1
Step 13: Processing a
- currentAtom = "a"
Step 14: Processing C
- currentAtom = "Ca"
- Count = 1
- atomCountMap["Ca"] = 1
- Reset currentAtom
Final Atom Count Map (Sorted)
Ca -> 1
H -> 4
Mg -> 1
O -> 4
Output Construction
Concatenating sorted atoms:
- "Ca"
- "H4"
- "Mg"
- "O4"
Final Output: "CaH4MgO4" ✅
Number of Atoms solution
Now, let's checkout the Number of Atoms solution in c++, Java, Python and JavaScript
"Number of Atoms" Code in all Languages.
1. Number of Atoms solution in C++ Try on Compiler
#include <iostream>
#include <stack>
#include <map>
#include <string>
#include <cctype>
#include <algorithm>
using namespace std;
string countOfAtoms(string formula) {
// Stack for multipliers
stack<int> multiplierStack;
multiplierStack.push(1);
// Map to count atoms
map<string, int> atomCountMap;
// Temporary atom and count
string currentAtom, currentCount;
// Total running multiplier
int runningMultiplier = 1;
// Traverse from right to left
int i = formula.size() - 1;
while (i >= 0) {
char ch = formula[i];
// If digit, prepend to currentCount
if (isdigit(ch)) {
currentCount = ch + currentCount;
}
// If lowercase letter
else if (islower(ch)) {
currentAtom = ch + currentAtom;
}
// If uppercase letter
else if (isupper(ch)) {
currentAtom = ch + currentAtom;
int count = currentCount.empty() ? 1 : stoi(currentCount);
atomCountMap[currentAtom] += count * runningMultiplier;
currentAtom.clear();
currentCount.clear();
}
// If closing parenthesis
else if (ch == ')') {
int multiplier = currentCount.empty() ? 1 : stoi(currentCount);
multiplierStack.push(multiplier);
runningMultiplier *= multiplier;
currentCount.clear();
}
// If opening parenthesis
else if (ch == '(') {
runningMultiplier /= multiplierStack.top();
multiplierStack.pop();
}
i--;
}
// Build result
string result;
for (auto& [atom, count] : atomCountMap) {
result += atom;
if (count > 1) result += to_string(count);
}
return result;
}
int main() {
string formula;
cin >> formula;
cout << countOfAtoms(formula) << endl;
return 0;
}
2. Number of Atoms solution in Java Try on Compiler
import java.util.*;
class Solution {
public String countOfAtoms(String formula) {
// Stores the valid multiplier for atoms being scanned
int runningMultiplier = 1;
// Stack to manage multipliers for nested parentheses
Stack<Integer> multiplierStack = new Stack<>();
multiplierStack.push(1); // Initial multiplier is 1
// Map to store the count of atoms
Map<String, Integer> atomCountMap = new HashMap<>();
// StringBuilders to store the current atom and its count
StringBuilder currentAtom = new StringBuilder();
StringBuilder currentCount = new StringBuilder();
// Traverse the formula from right to left
int index = formula.length() - 1;
while (index >= 0) {
char currentChar = formula.charAt(index);
// If the character is a digit, prepend it to currentCount
if (Character.isDigit(currentChar)) {
currentCount.insert(0, currentChar);
}
// If the character is a lowercase letter, prepend it to currentAtom
else if (Character.isLowerCase(currentChar)) {
currentAtom.insert(0, currentChar);
}
// If the character is an uppercase letter, the atom name is complete
else if (Character.isUpperCase(currentChar)) {
currentAtom.insert(0, currentChar);
int count = currentCount.length() > 0 ? Integer.parseInt(currentCount.toString()) : 1;
atomCountMap.put(currentAtom.toString(), atomCountMap.getOrDefault(currentAtom.toString(), 0) + count * runningMultiplier);
currentAtom.setLength(0);
currentCount.setLength(0);
}
// If we encounter a closing parenthesis `)`
else if (currentChar == ')') {
int multiplier = currentCount.length() > 0 ? Integer.parseInt(currentCount.toString()) : 1;
multiplierStack.push(multiplier);
runningMultiplier *= multiplier;
currentCount.setLength(0);
}
// If we encounter an opening parenthesis `(`
else if (currentChar == '(') {
runningMultiplier /= multiplierStack.pop();
}
index--;
}
TreeMap<String, Integer> sorted = new TreeMap<>(atomCountMap);
StringBuilder result = new StringBuilder();
for (Map.Entry<String, Integer> entry : sorted.entrySet()) {
result.append(entry.getKey());
if (entry.getValue() > 1) {
result.append(entry.getValue());
}
}
return result.toString();
}
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
String formula = scanner.nextLine();
Solution sol = new Solution();
System.out.println(sol.countOfAtoms(formula));
}
}
3. Number of Atoms solution in Python Try on Compiler
def countOfAtoms(formula: str) -> str:
from collections import defaultdict
# Stack to handle multipliers
multiplier_stack = [1]
# Running total multiplier
running_multiplier = 1
# Dictionary to count atoms
atom_count = defaultdict(int)
# Buffers for atom and count
atom = ""
count = ""
i = len(formula) - 1
while i >= 0:
char = formula[i]
# If digit, prepend to count
if char.isdigit():
count = char + count
# If lowercase letter
elif char.islower():
atom = char + atom
# If uppercase letter
elif char.isupper():
atom = char + atom
num = int(count) if count else 1
atom_count[atom] += num * running_multiplier
atom = ""
count = ""
# If closing parenthesis
elif char == ')':
mul = int(count) if count else 1
multiplier_stack.append(mul)
running_multiplier *= mul
count = ""
# If opening parenthesis
elif char == '(':
running_multiplier //= multiplier_stack.pop()
i -= 1
# Format result
return ''.join([key + (str(val) if val > 1 else '') for key, val in sorted(atom_count.items())])
if __name__ == "__main__":
formula = input()
print(countOfAtoms(formula))
4. Number of Atoms solution in JavaScript Try on Compiler
function countOfAtoms(formula) {
const multiplierStack = [1];
let runningMultiplier = 1;
const atomCountMap = new Map();
let atom = '';
let count = '';
for (let i = formula.length - 1; i >= 0; i--) {
const ch = formula[i];
// If digit
if (/\d/.test(ch)) {
count = ch + count;
}
// If lowercase letter
else if (/[a-z]/.test(ch)) {
atom = ch + atom;
}
// If uppercase letter
else if (/[A-Z]/.test(ch)) {
atom = ch + atom;
let num = count === '' ? 1 : parseInt(count);
atomCountMap.set(atom, (atomCountMap.get(atom) || 0) + num * runningMultiplier);
atom = '';
count = '';
}
// Closing parenthesis
else if (ch === ')') {
let mul = count === '' ? 1 : parseInt(count);
multiplierStack.push(mul);
runningMultiplier *= mul;
count = '';
}
// Opening parenthesis
else if (ch === '(') {
runningMultiplier /= multiplierStack.pop();
}
}
const result = [...atomCountMap.entries()]
.sort((a, b) => a[0].localeCompare(b[0]))
.map(([atom, count]) => atom + (count > 1 ? count : ''))
.join('');
return result;
}
// Read input using readline
const readline = require("readline");
const rl = readline.createInterface({
input: process.stdin,
output: process.stdout
});
rl.on("line", function (line) {
console.log(countOfAtoms(line));
rl.close();
});
Complexity Analysis of the problem
Time Complexity: O(n+m)
Let n be the length of the formula string.
- The while loop processes each character exactly once ⇒ O(n)
- Inside the loop:
- Operations like isdigit, islower, isupper, stoi, map insert/update, and stack push/pop are O(1) (except stoi, explained below).
- stoi(currentCount) is bounded by the number of digits — worst case O(log k), but k is typically small (e.g., "20", "100") — so we treat this as O(1) for practical inputs.
- Finally, building the result string involves:
- Iterating over atomCountMap → O(m), where m is the number of distinct atom types (bounded by alphabet size)
- String concatenation — amortized linear to total output length, which is ≤ O(n)
Time Complexity: O(n + m)
- n: length of the formula
- m: number of distinct atom types (typically much smaller than n)
Space Complexity: O(n)
Auxiliary Space Complexity
This includes temporary variables and data structures used during execution, not including input/output:
- multiplierStack: stores multipliers for nested parentheses — at most O(depth of nesting) ≤ O(n)
- atomCountMap: stores atom names and their counts — O(m)
- currentAtom, currentCount: max O(k), small strings (≪ n)
Auxiliary Space Complexity: O(n + m)
Total Space Complexity
This includes:
- Auxiliary space above
- Output string result: in worst case, each character is unique → O(n)
Total Space Complexity: O(n + m)