Number of 1 Bits Solution In C++/Java/Python/JS
Problem Description
Given a positive integer n, write a function that returns the number of set bits in its binary representation (also known as the Hamming weight).
What are Set Bits in Binary Representation?
In binary, a set bit is simply a bit whose value is 1. For example, if we take n = 11, its binary form is 1011, and it contains three set bits (two 1s at the ends and one in the middle). Our goal is to count how many such 1s are present in any given number’s binary form. This concept is also known as Hamming weight.
Example
Input: n = 11
Output: 3
Explanation: The input binary string 1011 has a total of three set bits.
Input: n = 128
Output: 1
Explanation: The input binary string 10000000 has a total of one set bit.
Input: n = 2147483645
Output: 30
Explanation: The input binary string 1111111111111111111111111111101 has a total of thirty set bits.
Constraints
- 1 <= n <= (2^31) - 1
Whenever we’re asked to count set bits (1s) in a number, our first instinct is simple — check each bit one by one. It’s the most natural way to begin, and it's where we build our understanding before exploring smarter tricks.
Brute Force Approach
Intuition
When we are given a number in decimal form (like 11 or 128), we know that inside the computer it is stored in binary — a sequence of 0s and 1s. These 0s and 1s are called bits, and each one represents whether a certain power of 2 is included in the number. Now, a set bit means a bit whose value is 1. So, when someone asks us to count the set bits in a number, they are really asking: “How many 1s are there in the binary form of this number?”
Let’s understand this with an example. Take n = 11. Its binary form is 1011. If we look at it closely, we see three 1s — the first, the second, and the fourth bits from the right. So the number of set bits (or 1s) in 11 is 3. Our task is to write a method that will take any number and tell us how many such 1s are present in its binary form.
Now let’s think — how can we check each bit of a number, one by one? The idea is very simple: we will repeatedly divide the number by 2, and in every step, we will check the remainder. Why? Because in binary, the remainder when dividing by 2 tells us the last bit of the number:
- If n % 2 = 1, that means the last bit is 1 (set bit).
- If n % 2 = 0, the last bit is 0 (not set).
Every time we find n % 2 == 1, we will increase our count by 1, because we found a set bit. Then we do n = n / 2, which drops the last bit, and we repeat the process with the remaining bits. This continues until the number becomes 0.
Approach
Step 1: Initialize Count
We begin by preparing a variable to keep track of how many 1s are present in the binary representation.
- Create a variable count and initialize it to 0.
- This variable will store the number of set bits found during iteration.
Step 2: Iterate Through the Bits
Now we loop through each bit of the number and check whether it's set (1) or not.
- The input number n is treated as a positive integer.
- Start a loop that continues while n is greater than 0.
- In each iteration check whether the least significant bit (LSB) is 1.
This is done using the condition n % 2 == 1. If true, increment count by 1. - Then, shift the number to the right to check the next bit. This is achieved using n = n / 2, which drops the last bit.
This loop continues until all bits have been examined.
Step 3: Return the Total Count
Once the loop finishes, we’ve gone through all the bits of the number. The count variable now holds the total number of 1s. Return count as the result.
Dry Run
Let’s do a detailed Dry Run for the given input to understand how the function counts the number of set bits (1s) in a number’s binary form:
Input: n = 11
Step 1: Initialize variables
We begin by initializing variables:
n = 11
count = 0 (to keep track of the number of set bits)
Step 2: Loop through each bit using while loop
We now check each bit of the number by performing % 2 and then dividing by 2 to move to the next bit.
First iteration:
n = 11
11 % 2 = 1 → last bit is 1 → increment count → count = 1
n = 11 / 2 = 5
Second iteration:
n = 5
5 % 2 = 1 → last bit is 1 → increment count → count = 2
n = 5 / 2 = 2
Third iteration:
n = 2
2 % 2 = 0 → last bit is 0 → count remains = 2
n = 2 / 2 = 1
Fourth iteration:
n = 1
1 % 2 = 1 → last bit is 1 → increment count → count = 3
n = 1 / 2 = 0 → loop ends
Step 3: Final result
The loop ends when n = 0.
We return the final count = 3.
Final Output
Output: 3
The number 11 in binary is 1011, which contains three set bits (1s).
Code for All Languages
C++
#include <iostream> // for cin and cout
using namespace std;
class Solution {
public:
// Function to count the number of set bits (1s) in the binary representation of a number
int hammingWeight(int n) {
// Step 1: Initialize a counter to store the number of set bits
int count = 0;
// Step 2: Iterate through each bit of the number
while (n > 0) {
// Check if the least significant bit is 1
if (n % 2 == 1) {
count++;
}
// Shift the number to the right by 1 to check the next bit
n = n / 2;
}
// Step 3: Return the total count of set bits
return count;
}
};
// Driver code
int main() {
int n;
// Input the number whose set bits are to be counted
cin >> n;
Solution sol;
// Call the function and print the result
cout << sol.hammingWeight(n);
return 0;
}Java
import java.util.Scanner; // for Scanner to read input
// Class that contains the logic to count set bits
class Solution {
// Function to count the number of set bits (1s) in the binary representation of a number
public int hammingWeight(int n) {
// Step 1: Initialize a counter to store the number of set bits
int count = 0;
// Step 2: Iterate through each bit of the number
while (n > 0) {
// Check if the least significant bit is 1
if (n % 2 == 1) {
count++;
}
// Shift the number to the right by 1 to check the next bit
n = n / 2;
}
// Step 3: Return the total count of set bits
return count;
}
}
// Driver class
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n;
// Input the number whose set bits are to be counted
n = sc.nextInt();
Solution sol = new Solution();
// Call the function and print the result
System.out.println(sol.hammingWeight(n));
}
}Python
class Solution:
# Function to count the number of set bits (1s) in the binary representation of a number
def hammingWeight(self, n: int) -> int:
# Step 1: Initialize a counter to store the number of set bits
count = 0
# Step 2: Iterate through each bit of the number
while n > 0:
# Check if the least significant bit is 1
if n % 2 == 1:
count += 1
# Shift the number to the right by 1 to check the next bit
n = n // 2
# Step 3: Return the total count of set bits
return count
# Driver code
if __name__ == "__main__":
# Input the number whose set bits are to be counted
n = int(input())
sol = Solution()
# Call the function and print the result
print(sol.hammingWeight(n))Javascript
/**
* Function to count the number of set bits (1s) in the binary representation of a number
* @param {number} n
* @return {number}
*/
var hammingWeight = function(n) {
// Step 1: Initialize a counter to store the number of set bits
let count = 0;
// Step 2: Iterate through each bit of the number
while (n > 0) {
// Check if the least significant bit is 1
if (n % 2 === 1) {
count++;
}
// Shift the number to the right by 1 to check the next bit
n = Math.floor(n / 2);
}
// Step 3: Return the total count of set bits
return count;
};
// Driver code
const readline = require('readline');
const rl = readline.createInterface({
input: process.stdin,
output: process.stdout
});
// Input the number whose set bits are to be counted
rl.question('', function(input) {
const n = parseInt(input);
console.log(hammingWeight(n));
rl.close();
});Time Complexity: O(log(n))
Iterating Through Each Bit: O(log n)
We use a while loop that continues until n becomes 0.
In each iteration, we check whether the least significant bit is set (n % 2), and then divide the number by 2.
Each division by 2 effectively removes one bit from the binary representation of n.
So, the number of iterations is equal to the number of bits required to represent the number, which is log₂(n).
Each operation inside the loop (modulus, addition, division) takes constant time.
Final Time Complexity: O(log n)
The total number of operations depends on how many bits the number has, i.e., log₂(n).
There are no nested loops, no recursion, and no extra data structures.
Hence, the algorithm runs in logarithmic time with respect to the input number n.
Space Complexity: O(1)
Auxiliary Space Complexity: O(1)
This refers to the additional memory used during computation, not including the input/output.
In this program, Only a few fixed-size variables are used:
- count to store the number of set bits
- n for computation (modified in place) These variables occupy constant space regardless of the size of the input number.
- No dynamic data structures like arrays are used to store the binary form.
Hence, the auxiliary space used is constant, i.e., O(1).
Total Space Complexity: O(1)
This includes auxiliary space and any input/output related storage.
In this program:
- Input variable n is an integer, which occupies constant space.
- The output is directly printed using cout without storing it.
- There are no data structures or arrays that grow with the size of the input.
Therefore, the total space required remains constant, i.e., O(1).
After trying the basic approach, a thought naturally arises — do we really need to check every single bit, even the zeroes? What if we could somehow jump directly from one set bit to the next? That's where the real play with bits begins.
Optimal Approach
Intuition
When we are told to count the number of set bits (i.e., 1s) in the binary representation of a number, our first natural idea — or brute-force approach — is to check each bit individually. This is like scanning the number from right to left and asking: Is this bit a 1? If yes, count it. And how do we usually check a single bit? We use the bitwise AND operator — for example, check if n & 1 == 1, then right-shift the number, and continue. So if the number has 32 bits (like in a standard integer), we’d end up doing 32 operations, one for each bit — regardless of how many 1s there actually are.
But here’s the important realization: we are only interested in the bits that are set to 1, not the zeros. So, what if there was a way to jump directly from one set bit to the next and ignore all the zeros in between? That’s where a brilliant technique called Brian Kernighan’s Algorithm comes in. This algorithm leverages a powerful observation: whenever we perform n = n & (n - 1), the rightmost set bit of n gets cleared. This means, in one operation, we eliminate one 1 from the number — no need to scan each bit manually!
How does n & (n - 1) Work?
We are using the expression n & (n - 1) to remove the rightmost set bit (the rightmost 1) from a number. But how does it actually do that?
Let’s begin by recalling one important truth about the AND operation:
- 1 & 1 = 1
- 1 & 0 = 0
- 0 & 1 = 0
- 0 & 0 = 0
So, an AND only gives 1 if both bits are 1.
Now, to understand what n & (n - 1) does, we must understand how subtraction affects the binary form of a number.
example:
Suppose:
- n = 12
- Binary of 12 is 1100
Now subtract 1:
- n - 1 = 11
- Binary of 11 is 1011
Now perform the operation:
- n = 1100
- n - 1 = 1011
Now apply AND bit-by-bit:
1100 (12)
& 1011 (11)
= 1000 (8)
As we can see, the result is 1000, which is 8 — the rightmost set bit has been removed!
- Subtracting 1 from a number flips all bits after the rightmost set bit, including the rightmost set bit itself.
- When we then do AND with the original number, it turns that rightmost 1 into a 0, and all the 0s after it stay 0.
So instead of looping 32 times for a 32-bit number, we only loop as many times as there are 1s in the binary form. If a number has 3 set bits, the loop runs just 3 times. That’s a massive improvement! You’re not sweeping the whole floor — you’re just jumping to the spots where dust actually exists and cleaning only those. This is not just efficient but also elegant — and it shows the power of understanding bitwise operations deeply.
Approach
Step 1: Initialize Count
We begin by creating a variable to track the number of set bits (1s) in the binary form of the number.
Create a variable count and initialize it to 0.
This variable will be incremented each time a set bit is found and removed from the number.
Step 2: Repeatedly Remove Rightmost Set Bit
We now iterate through the number, removing one set bit at a time using a smart bitwise trick.
Start a loop that continues as long as n > 0.
Inside the loop:
- Use the expression n = n & (n - 1) to remove the rightmost set bit from n.
- Each time this operation is performed, exactly one 1 is removed from n.
- After updating n, increment count by 1 to record the removed set bit.
This continues until n becomes 0, which means no set bits are left.
Step 3: Return the Total Count
After the loop ends, all the set bits have been removed one by one.
The variable count now holds the total number of 1s in the binary representation of the input number.
Return count as the result.
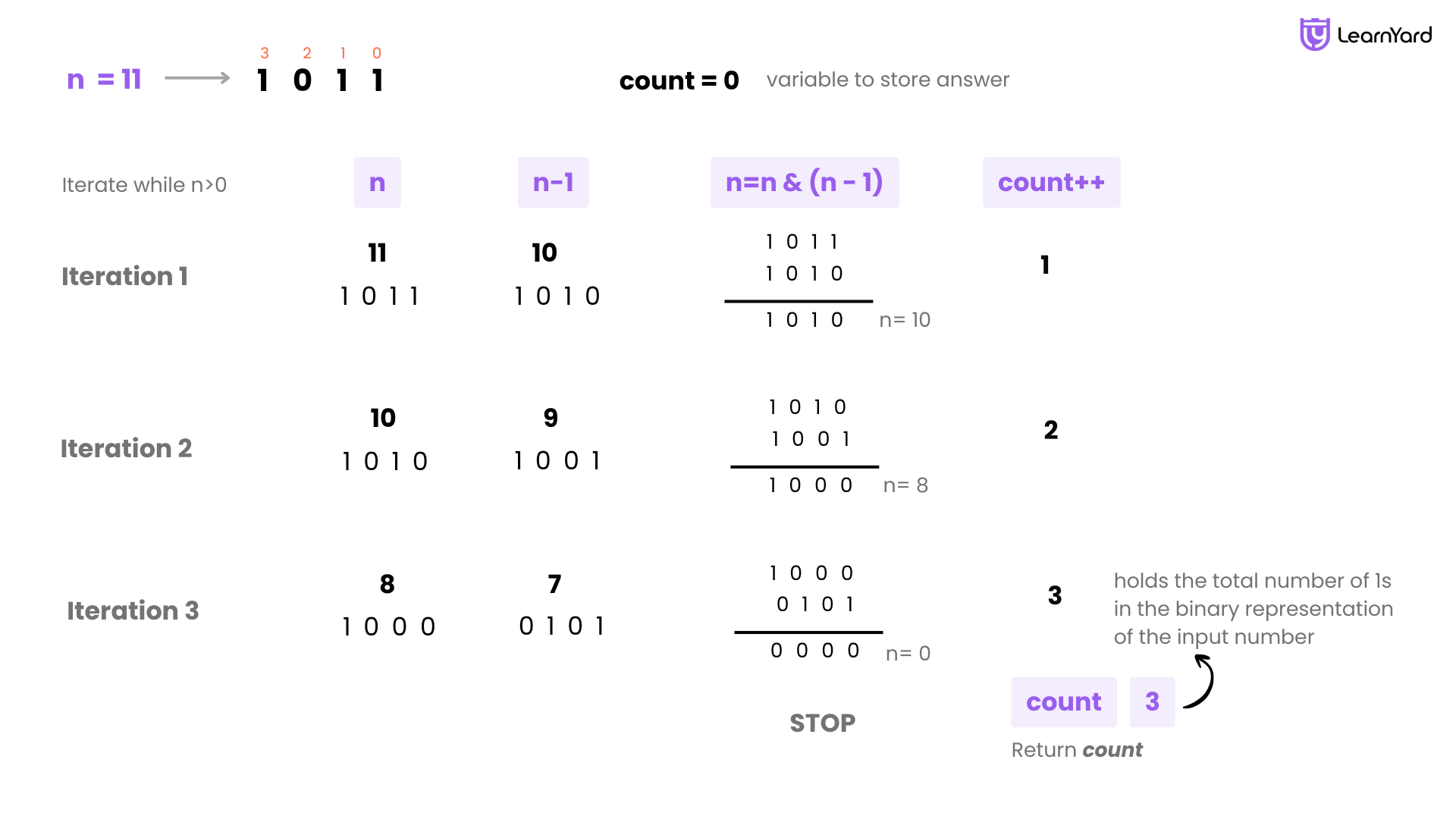
Dry Run
Let’s do a detailed Dry Run for the set bit counting function using Brian Kernighan’s Algorithm:
Input: n = 11
We want to count the number of 1s in the binary representation of 11.
Step 1: Understand the Binary Form
The binary representation of 11 is 1011
This has three 1s, so the output should be 3
Step 2: Initialize
We initialize:
- count = 0
We now enter the loop:
while (n > 0)
First Iteration:
- n = 11 → binary = 1011
- Perform n & (n - 1) → 11 & 10 → 1011 & 1010 = 1010 (which is 10)
- Update n = 10
- Increment count = 1
Second Iteration:
- n = 10 → binary = 1010
- Perform n & (n - 1) → 10 & 9 → 1010 & 1001 = 1000 (which is 8)
- Update n = 8
- Increment count = 2
Third Iteration:
- n = 8 → binary = 1000
- Perform n & (n - 1) → 8 & 7 → 1000 & 0111 = 0000 (which is 0)
- Update n = 0
- Increment count = 3
Step 3: Exit Loop
Now, n = 0, so the loop ends.
Final Output:
The final value of count = 3
So, the number of set bits in 11 is:
Output: 3
Code for All Languages
C++
#include <iostream> // for cin and cout
using namespace std;
class Solution {
public:
// Function to count the number of set bits (1s) using Brian Kernighan’s Algorithm
int hammingWeight(int n) {
// Step 1: Initialize a counter to store the number of set bits
int count = 0;
// Step 2: Keep turning off the rightmost set bit until n becomes 0
while (n > 0) {
// Remove the rightmost set bit
n = n & (n - 1);
count++;
}
// Step 3: Return the total count of set bits
return count;
}
};
// Driver code
int main() {
int n;
// Input the number whose set bits are to be counted
cin >> n;
Solution sol;
// Call the function and print the result
cout << sol.hammingWeight(n);
return 0;
}Java
import java.util.Scanner; // for Scanner to read input
// Class that contains the logic to count set bits
class Solution {
// Function to count the number of set bits (1s) using Brian Kernighan’s Algorithm
public int hammingWeight(int n) {
// Step 1: Initialize a counter to store the number of set bits
int count = 0;
// Step 2: Keep turning off the rightmost set bit until n becomes 0
while (n > 0) {
// Remove the rightmost set bit
n = n & (n - 1);
count++;
}
// Step 3: Return the total count of set bits
return count;
}
}
// Driver class
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n;
// Input the number whose set bits are to be counted
n = sc.nextInt();
Solution sol = new Solution();
// Call the function and print the result
System.out.println(sol.hammingWeight(n));
}
}
Python
class Solution:
# Function to count the number of set bits (1s) in the binary representation of a number
def hammingWeight(self, n: int) -> int:
# Step 1: Initialize a counter to store the number of set bits
count = 0
# Step 2: Keep turning off the rightmost set bit until n becomes 0
while n > 0:
# Remove the rightmost set bit
n = n & (n - 1)
count += 1
# Step 3: Return the total count of set bits
return count
# Driver code
if __name__ == "__main__":
# Input the number whose set bits are to be counted
n = int(input())
sol = Solution()
# Call the function and print the result
print(sol.hammingWeight(n))
Javascript
/**
* Function to count the number of set bits (1s) in the binary representation of a number
* @param {number} n
* @return {number}
*/
var hammingWeight = function(n) {
// Step 1: Initialize a counter to store the number of set bits
let count = 0;
// Step 2: Keep turning off the rightmost set bit until n becomes 0
while (n > 0) {
// Remove the rightmost set bit
n = n & (n - 1);
count++;
}
// Step 3: Return the total count of set bits
return count;
};
// Driver code
const readline = require('readline');
const rl = readline.createInterface({
input: process.stdin,
output: process.stdout
});
// Input the number whose set bits are to be counted
rl.question('', function(input) {
const n = parseInt(input);
console.log(hammingWeight(n));
rl.close();
});
Time Complexity: O(log(n))
Rightmost Set Bit Removal Loop: O(number of set bits)
The while loop runs as long as n > 0.
In each iteration, the expression n = n & (n - 1) removes the rightmost set bit from n.
This means that the loop runs exactly as many times as there are 1s (set bits) in the binary representation of n.
So, the number of iterations is equal to the number of set bits in n, let's say k.
Each Bitwise Operation Inside Loop: O(1)
The operation n & (n - 1) and count++ both are constant-time operations.
Thus, each iteration of the loop takes O(1) time.
Final Time Complexity: O(k)
Since the loop runs k times and each iteration is O(1),
The total time complexity is O(k), where k is the number of set bits in n.
In the worst case (e.g., when all bits are 1), this could go up to O(log n) because the maximum number of set bits is bounded by the number of bits in n.
So, Worst Case Time Complexity: O(log n). Best/Average Case Time Complexity: O(k) depending on the number of set bits.
Space Complexity: O(1)
Auxiliary Space Complexity: O(1)
This measures the extra memory used during computation, excluding input and output storage. In this program:
- Only a few fixed-size integer variables are used: count, n (function parameter), and loop control variable.
- There are no arrays, dynamic memory allocations, or additional data structures.
- The algorithm performs all operations in-place without requiring extra space.
Thus, the auxiliary space remains constant, i.e., O(1).
Total Space Complexity: O(1)
This accounts for both auxiliary space and the space used for input and output:
- The input number n and the result are both simple integers.
- Input is read using cin, and output is printed directly using cout without storing it.
- No additional memory is allocated beyond a few integer variables.
Therefore, the total space usage remains constant, i.e., O(1).
Similar Problems
Given two positive integer n and k, check if the kth index bit of n is set or not.
Note: A bit is called set if it is 1.
Given a non-negative number n. The problem is to set the rightmost unset bit in the binary representation of n.