Minimum Score by Changing Two Elements Solution In C++/Java/Python/JS
Problem Description
You are given an integer array nums.
The low score of nums is the minimum absolute difference between any two integers.
The high score of nums is the maximum absolute difference between any two integers.
The score of nums is the sum of the high and low scores.
Return the minimum score after changing two elements of nums.
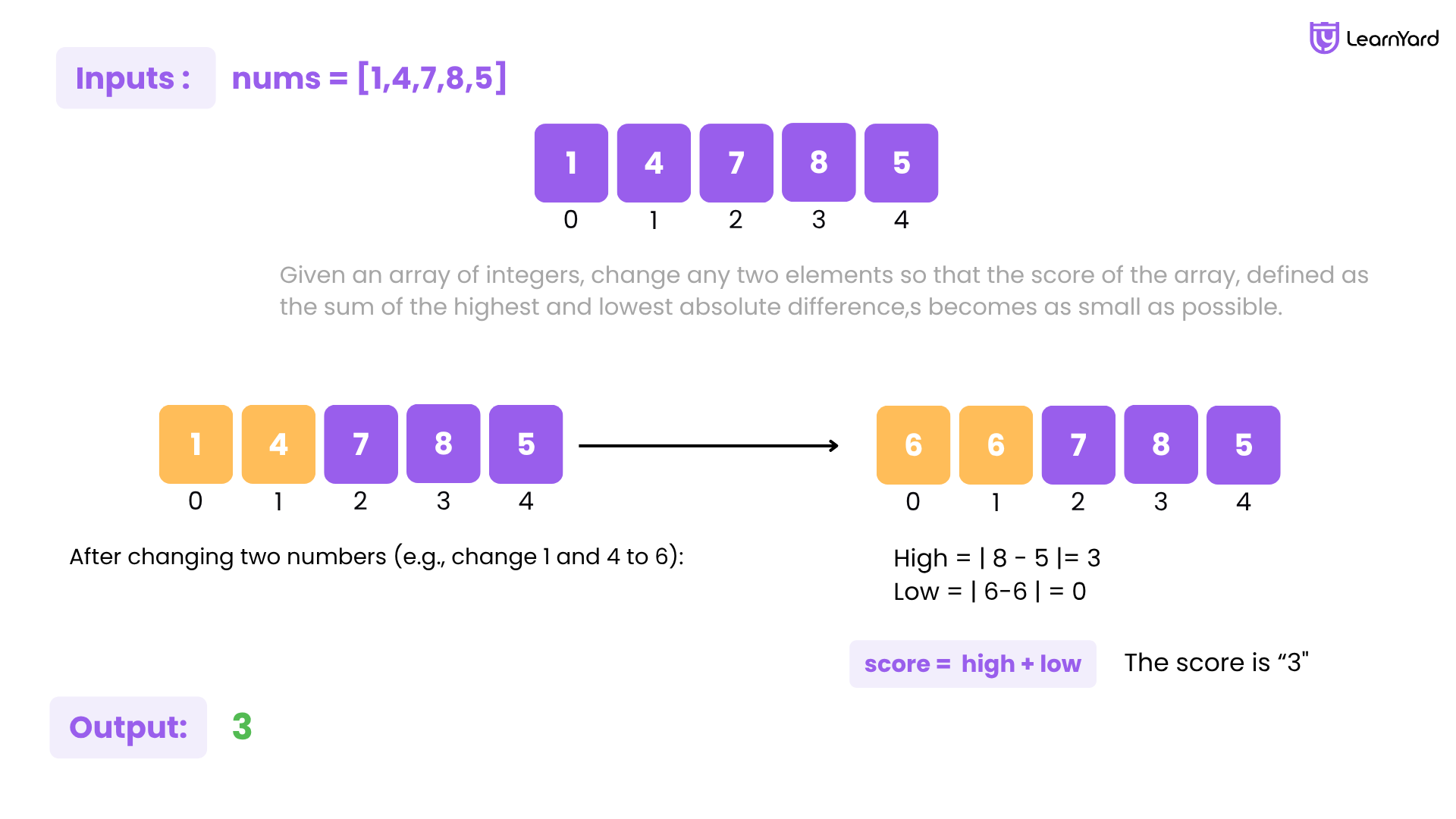
Example
Input: nums = [1,4,7,8,5]
Output: 3
Explanation:
- Change nums[0] and nums[1] to be 6 so that nums becomes [6,6,7,8,5].
- The low score is the minimum absolute difference: |6 - 6| = 0.
- The high score is the maximum absolute difference: |8 - 5| = 3.
- The sum of high and low score is 3.
Input: nums = [1,4,3]
Output: 0
Explanation:
- Change nums[1] and nums[2] to 1 so that nums becomes [1,1,1].
- The sum of maximum absolute difference and minimum absolute difference is 0.
Constraints
- 3 <= nums.length <= 105
- 1 <= nums[i] <= 109
Figuring out "Minimum Score by Changing Two Elements" can be solved using different approaches. We will first figure out the most intuitive approach and move to the optimal approach if exists. Let's sit with a pen and paper and figure out the algorithm !!
Optimal Approach
Intuition
We have an integer array, and we need to modify at most two elements to minimize the sum of the maximum absolute difference and the minimum absolute difference. Before jumping into the solution, how do you think we should approach this problem?
Since we can change two elements, maybe we should focus on the largest and smallest values?
That’s a great observation! The high score is determined by the largest difference, and the low score is the smallest difference. But before deciding which elements to change, let’s take a small example and analyze it step by step.
Consider the array: [10, 1, 3, 8, 5].
- What do you think we should do first?
Sorting could help because then we can easily identify the smallest and largest elements.
Exactly! Sorting gives us an ordered structure, making it easier to find key values.
After sorting: [1, 3, 5, 8, 10].
- High score: The maximum absolute difference is 10 - 1 = 9.
- Low score: The minimum absolute difference is |3 - 1| = 2.
- Total score = 9 + 2 = 11.
But we can change at most two elements. So, which elements should we consider changing?
Maybe the smallest and largest elements?
Good thinking! Changing the extreme values would reduce the high score. But we also need to ensure the low score remains minimal. Let’s analyze possible modifications.
Observations:
- If we change the first two elements to a value close to the third element, we can potentially reduce the low score.
- The smallest numbers in the array create the largest gap with the biggest numbers. By increasing the smallest values to something closer to the middle of the array, we shrink that gap, lowering the maximum difference.
- Additionally, if the first two numbers are brought closer together, the smallest absolute difference (low score) also reduces, making the total sum smaller.
- If we change the last two elements to a value close to the third-to-last element, we can reduce the high score.
- The largest values in the array contribute most to the maximum difference. If we lower them closer to the middle, the high score decreases.
- However, we must check whether this change increases the smallest absolute difference, as that would affect the total score.
- If we change one element from the start and one from the end, we need to carefully choose which ones.
- Instead of modifying only the smallest or largest values, we can adjust both ends toward the middle to balance the overall spread of numbers.
- The goal is to bring the two extreme values closer while ensuring that the smallest absolute difference does not increase too much. This approach provides another way to minimize the total score.
Exploring the Cases:

Conclusion:
Looking at these cases, the minimum score achievable is 4 when we change the last two elements to a value close to the third-to-last element.
Well summarized! Now, if you think about it, what kind of approach are we using here?
We are carefully choosing which elements to modify in a way that immediately reduces the high and low scores without considering all possible changes. This sounds like a greedy algorithm!
Exactly! The greedy approach works well here because, at each step, we make the most effective modification to minimize the total score, ensuring that we focus only on the most impactful changes.
Let's now see how our algorithm looks!
Minimum Score by Changing Two Elements Algorithm
We implement the solution using a greedy approach to minimize the sum of the maximum and minimum absolute differences.
- Sort the Array: Sorting helps us quickly identify the smallest and largest elements, making it easier to decide which values to modify.
- Identify Key Transformations: Since we can change at most two elements, we consider three possible ways to minimize the score:
- Change the first two elements to match the third, reducing the smallest differences.
- Change the last two elements to match the third-to-last, reducing the largest difference.
- Change one element from the start and one from the end to bring extremes closer to the middle.
- Compute the Minimum Score: By evaluating these three options, we determine the smallest possible total score after modification.
- Return the Minimum Result: The best modification among the three options gives the optimal answer.
Fine !! Let's now see how to code the approach !!
Approach
- Sort the Array: Sorting helps us structure the numbers in increasing order, making it easier to identify the largest and smallest absolute differences.
- Consider Three Possible Modifications:
- Modify the first two elements to match the third element, reducing the smallest absolute difference.
- Modify the last two elements to match the third-to-last element, reducing the largest absolute difference.
- Modify one element from the start and one from the end to bring extreme values closer to the middle.
- Compute the Minimum Score:
- For each modification, calculate the new maximum absolute difference and minimum absolute difference.
- Track the smallest possible total score after these changes.
- Return the Best Result: The minimum value among the three computed scores is our final answer, ensuring the most optimal modification strategy.
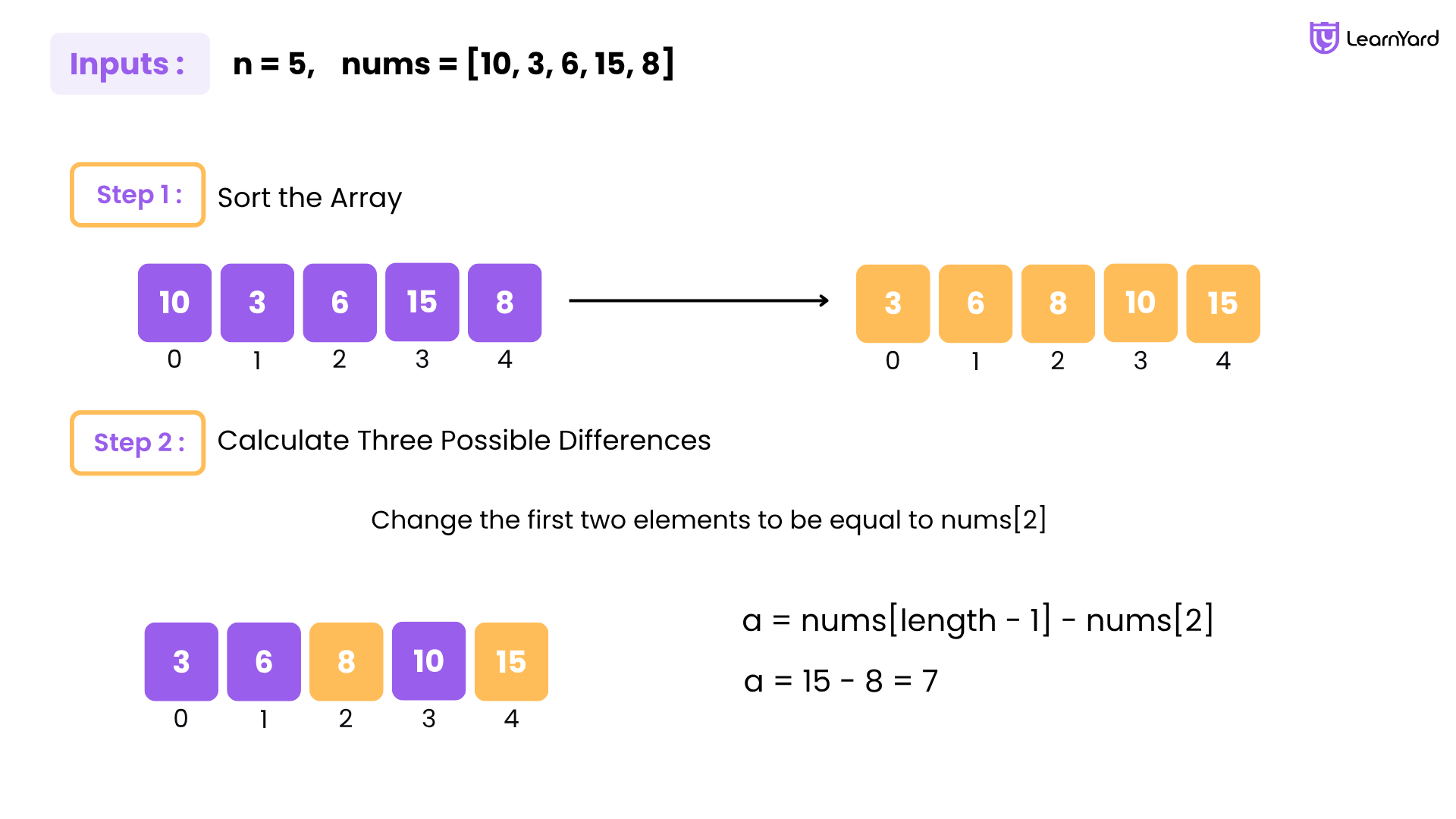

Dry-Run
Example Input:
n = 5
nums = [10, 3, 6, 15, 8]
Step-by-Step Dry Run
Sort the Array
Before Sorting: [10, 3, 6, 15, 8]
After Sorting: [3, 6, 8, 10, 15]
Calculate Three Possible Differences
Option 1: Change the first two elements to be equal to nums[2]
- a = nums[length - 1] - nums[2]
- a = 15 - 8 = 7
Option 2: Change the last two elements to be equal to nums[length-2]
- b = nums[length - 2] - nums[1]
- b = 10 - 6 = 4
Option 3: Change the first and last element to be nums[1] and nums[length-2]
- c = nums[length - 3] - nums[0]
- c = 8 - 3 = 5
Step 3: Find the Minimum Value
- We have three possible values: a = 7, b = 4, c = 5
- Minimum Score: min(7, 4, 5) = 4
Final Output: 4
Minimum Score by Changing Two Elements Solution
Now let's checkout the "Minimum Score by Changing Two Elements" code in C++, Java, Python and JavaScript.
"Minimum Score by Changing Two Elements" Code in all Languages.
1. Minimum Score by Changing Two Elements solution in C++ Try on Compiler
class Solution {
public:
int minimizeSum(vector<int>& nums) {
// Sort the array to establish a non-decreasing order
sort(nums.begin(), nums.end());
int length = nums.size();
// Calculate the three possible differences
// Option 1: Change the first two elements to be equal to nums[2]
int a = nums[length - 1] - nums[2];
// Option 2: Change the last two elements to be equal to nums[length-2]
int b = nums[length - 2] - nums[1];
// Option 3: Change the first and last element to be nums[1] and nums[length-2]
int c = nums[length - 3] - nums[0];
// Return the minimum value among a, b, and c
return min(a, min(b, c));
}
};2. Minimum Score by Changing Two Elements Solution in Java Try on Compiler
class Solution {
public int minimizeSum(int[] nums) {
// Sort the array to establish a non-decreasing order
Arrays.sort(nums);
int length = nums.length;
// Calculate the three possible differences
// Option 1: Change the first two elements to be equal to nums[2]
int a = nums[length - 1] - nums[2];
// Option 2: Change the last two elements to be equal to nums[length-2]
int b = nums[length - 2] - nums[1];
// Option 3: Change the first and last element to be nums[1] and nums[length-2]
int c = nums[length - 3] - nums[0];
// Return the minimum value among a, b, and c
return Math.min(a, Math.min(b, c));
}
}3. Minimum Score by Changing Two Elements Solution in Python Try on Compiler
class Solution:
def minimizeSum(self, nums: List[int]) -> int:
# Sort the array to establish a non-decreasing order
nums.sort()
length = len(nums)
# Calculate the three possible differences
# Option 1: Change the first two elements to be equal to nums[2]
a = nums[length - 1] - nums[2]
# Option 2: Change the last two elements to be equal to nums[length-2]
b = nums[length - 2] - nums[1]
# Option 3: Change the first and last element to be nums[1] and nums[length-2]
c = nums[length - 3] - nums[0]
# Return the minimum value among a, b, and c
return min(a, b, c)4. Minimum Score by Changing Two Elements solution in JavaScript Try on Compiler
/**
* @param {number[]} nums
* @return {number}
*/
var minimizeSum = function(nums) {
// Sort the array to establish a non-decreasing order
nums.sort((a, b) => a - b);
const length = nums.length;
// Calculate the three possible differences
// Option 1: Change the first two elements to be equal to nums[2]
let a = nums[length - 1] - nums[2];
// Option 2: Change the last two elements to be equal to nums[length-2]
let b = nums[length - 2] - nums[1];
// Option 3: Change the first and last element to be nums[1] and nums[length-2]
let c = nums[length - 3] - nums[0];
// Return the minimum value among a, b, and c
return Math.min(a, Math.min(b, c));
};Minimum Score by Changing Two Elements Complexity Analysis
Time Complexity: O(n log n)
Sorting the array → O(n log n)
→ The sort(nums) function sorts the array, which takes O(n log n).
Computing three differences (a, b, c) → O(1)
→ These are simple arithmetic operations that run in constant time.
Finding the minimum of three values operates in constant time. → O(1)
Overall Time Complexity:
- O(n log n) + O(1) = O(n log n)
- Sorting dominates, so the final complexity is O(n log n).
Space Complexity: O(1)
Auxiliary space (variables: a, b, c, length) → O(1)
→ Only a few integer variables are used, which take constant space.
Sorting is done in-place (sort(nums)) → O(1) auxiliary space
Thus, Total Space Complexity = O(1).
Similar Problems
You are given an integer array nums.
In one move, you can choose one element of nums and change it to any value.
Return the minimum difference between the largest and smallest value of nums after performing at most three moves.
There are n gas stations along a circular route, where the amount of gas at the ith station is gas[i].
You have a car with an unlimited gas tank and it costs cost[i] of gas to travel from the ith station to its next (i + 1)th station. You begin the journey with an empty tank at one of the gas stations.
Given two integer arrays gas and cost, return the starting gas station's index if you can travel around the circuit once in the clockwise direction, otherwise return -1. If there exists a solution, it is guaranteed to be unique.