Minimum Operations to Make Array Equal II Solution In C++/Java/Python/JS
Problem Description
You are given two integer arrays nums1 and nums2 of equal length n and an integer k. You can perform the following operation on nums1:
Choose two indexes i and j and increment nums1[i] by k and decrement nums1[j] by k. In other words, nums1[i] = nums1[i] + k and nums1[j] = nums1[j] - k.
nums1 is said to be equal to nums2 if for all indices i such that 0 <= i < n, nums1[i] == nums2[i].
Return the minimum number of operations required to make nums1 equal to nums2. If it is impossible to make them equal, return -1.
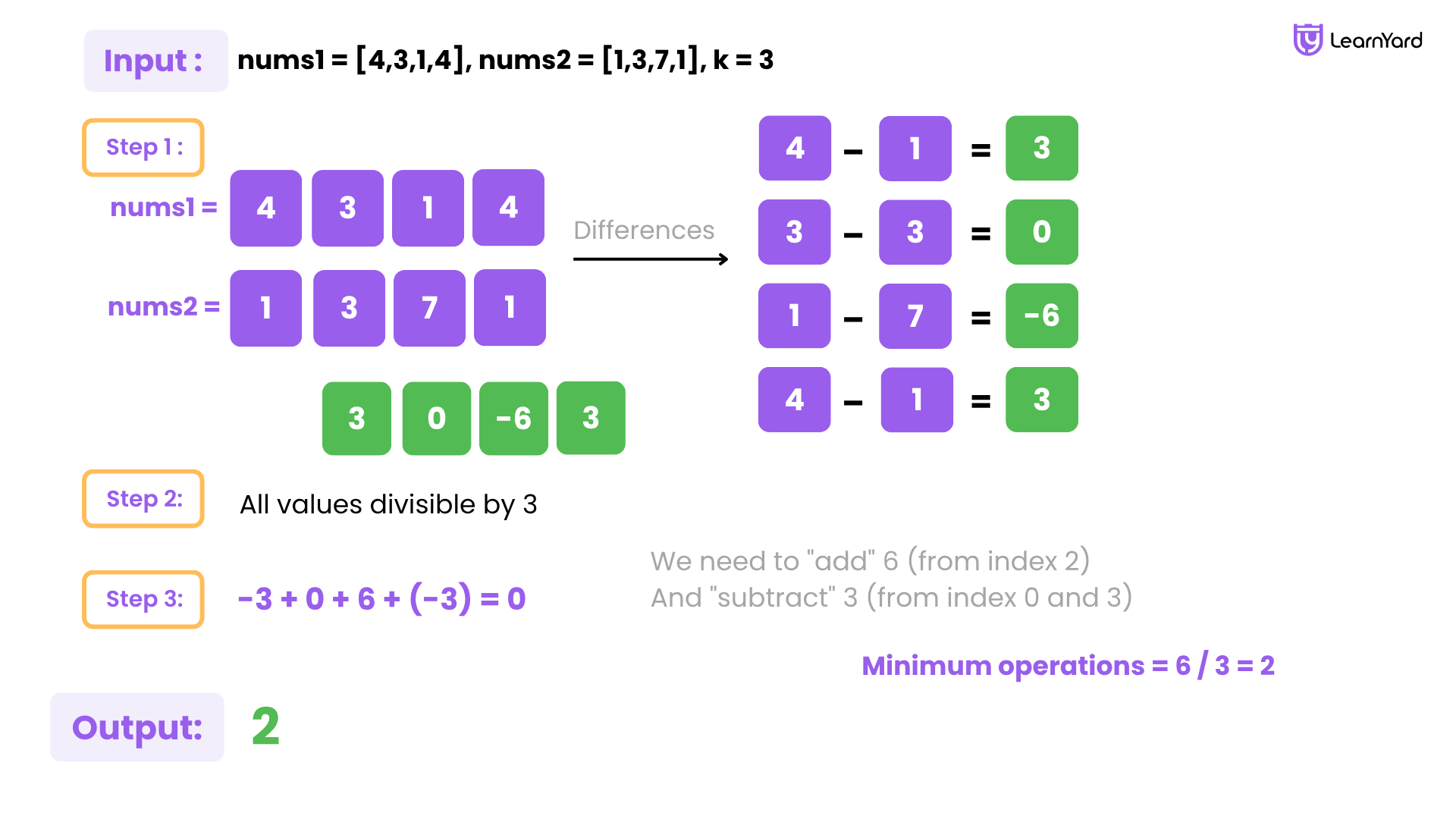
Example
Input: nums1 = [4,3,1,4], nums2 = [1,3,7,1], k = 3
Output: 2
Explanation: In 2 operations, we can transform nums1 to nums2.
1st operation: i = 2, j = 0. After applying the operation, nums1 = [1,3,4,4].
2nd operation: i = 2, j = 3. After applying the operation, nums1 = [1,3,7,1].
One can prove that it is impossible to make arrays equal in fewer operations.
Input: nums1 = [3,8,5,2], nums2 = [2,4,1,6], k = 1
Output: -1
Explanation: It can be proved that it is impossible to make the two arrays equal.
Constraints
- n == nums1.length == nums2.length
- 2 <= n <= 105
- 0 <= nums1[i], nums2[j] <= 109
- 0 <= k <= 105
Figuring out "Minimum Operations to Make Array Equal II" can be solved using different approaches. We will first figure out the most intuitive approach and move to the optimal approach if exists. Let's sit with a pen and paper and figure out the algorithm !!
Optimal Approach
Intuition
We have two arrays, nums1 and nums2, and we can perform an operation where we increment one element of nums1 by k and decrement another element by k. The goal is to make nums1 identical to nums2 in the minimum number of steps. If it's impossible, we return -1.
So, how do you think we should approach this problem?
Well, the most direct way would be to keep making changes in nums1 until it matches nums2, but that seems inefficient. Maybe we need to look at the differences between nums1 and nums2 first?
Exactly! Instead of focusing on individual elements, let's analyze the difference array:
diff[i] = nums2[i] - nums1[i]
Each element in diff represents how much nums1[i] needs to increase (if positive) or decrease (if negative) to match nums2[i].
Now, let’s take a simple example:
Example:
nums1 = [6, 7, 3, 12, 1]
nums2 = [3, 7, 9, 3, 7]
k = 3
Computing diff:
diff = [3 - 6, 7 - 7, 9 - 3, 3 - 12, 7 - 1] = [-3, 0, 6, -9, 6]
This tells us:
- nums1[0] needs to decrease by 3.
- nums1[1] is already correct.
- nums1[2] needs to increase by 6.
- nums1[3] needs to decrease by 9.
- nums1[4] needs to increase by 6.
So, we should try to balance the increases and decreases using the allowed operation?
Yes, but let’s think about possibilities first. Since we can only increment or decrement by k, each diff[i] must be a multiple of k. Otherwise, we can’t reach nums2[i] from nums1[i] exactly.
So, our first check is:
for each diff[i]: if diff[i] % k != 0, return -1
Does that make sense?
Got it! If any difference isn’t a multiple of k, we immediately return -1 since it’s impossible to achieve the transformation.
Great! Now, assuming all differences are multiples of k, what next?
Let’s rewrite the differences as:
diff = [-3, 0, 6, -9, 6]
Divide each element by k = 3 to get the number of operations needed:
diff' = [-1, 0, 2, -3, 2]
This means:
- We need 1 -k operation.
- We need 0 operations for the second element.
- We need 2 +k operations.
- We need 3 -k operations.
- We need 2 +k operations.
Oh! The total +k operations must equal the total -k operations, otherwise, we can’t balance the transformations, right?
Exactly! If the sum of diff' is not zero, return -1.
If it is zero, then the number of operations needed is simply the total number of positive operations (or negative operations, since they should be equal).
So, the minimum operations required for the above example is 4, since we need 4 +k operations (2 from nums1[2] and 2 from nums1[4]), which balance out the 4 -k operations (1 from nums1[0] and 3 from nums1[3]).
Final Steps:
- Check if all diff[i] are multiples of k.
- Check if sum(diff') is zero.
- Return the total number of positive operations.
Well summarized! Now, if we think about it, what kind of approach are we using here?
We are making the best possible choice at each step without looking ahead too much. This sounds like a greedy algorithm!
Exactly! The greedy approach works perfectly here because, at each step, we are ensuring that we efficiently balance the required increments and decrements without needing to explore all possible sequences.
Let's now see how our algorithm looks!
Minimum Operations to Make Array Equal II Algorithm
We implement this solution using a greedy approach.
Instead of explicitly storing a diff array, we compute differences on the fly while iterating through nums1 and nums2.
Edge Case: Handle k = 0 First
- If k = 0, no operations can be performed.
- If nums1 is already equal to nums2, return 0 (no changes needed).
- Otherwise, return -1 (since transformation is impossible).
In the minOperations Method, We Maintain Two Values:
- increase → Total number of +k operations needed.
- decrease → Total number of -k operations needed.
Update Conditions:
- Compute diff = nums2[i] - nums1[i] for each element.
- If diff is not a multiple of k, return -1 (impossible case).
- If diff > 0, add diff / k to increase.
- If diff < 0, add -diff / k to decrease.
Final Check:
- If increase equals decrease, return either of them as the minimum steps required.
- Otherwise, return -1 (since the operations cannot be balanced).
Fine !! Let's now see how to code the approach !!
Approach
We use a greedy approach to efficiently determine the minimum operations required to transform nums1 into nums2. Instead of explicitly storing a diff array, we compute and process differences on the fly while iterating.
Edge Case: Handle k = 0 First
- If k = 0, we cannot modify nums1.
- If nums1 is already equal to nums2, return 0.
- Otherwise, return -1 (since transformations are impossible).
Initialize Two Counters:
- increase = 0 → Tracks the total number of +k operations needed.
- decrease = 0 → Tracks the total number of -k operations needed.
Iterate Through the Arrays:
- Compute diff = nums2[i] - nums1[i] for each index i.
- If diff % k != 0, return -1 (impossible transformation).
- If diff > 0, update increase += diff / k (we need positive operations).
- If diff < 0, update decrease += -diff / k (we need negative operations).
Return:
- If increase == decrease, return either of them as the minimum steps required.
- Otherwise, return -1 (since the operations cannot be balanced).
Let us understand this with a video,
Dry-Run
Example Input
n = 6
nums1 = [5, 2, 8, 3, 10, 7]
nums2 = [11, 5, 11, 0, 7, 10]
k = 3
Step-by-Step Dry Run
- Index 0:
→ nums1[0] = 5, nums2[0] = 11
→ diff = 11 - 5 = 6
→ 6 % 3 == 0 (Valid)
→ +2 operations needed → increase = 2, decrease = 0 - Index 1:
→ nums1[1] = 2, nums2[1] = 5
→ diff = 5 - 2 = 3
→ 3 % 3 == 0 (Valid)
→ +1 operation needed → increase = 3, decrease = 0 - Index 2:
→ nums1[2] = 8, nums2[2] = 11
→ diff = 11 - 8 = 3
→ 3 % 3 == 0 (Valid)
→ +1 operation needed → increase = 4, decrease = 0 - Index 3:
→ nums1[3] = 3, nums2[3] = 0
→ diff = 0 - 3 = -3
→ -3 % 3 == 0 (Valid)
→ -1 operation needed → increase = 4, decrease = 1 - Index 4:
→ nums1[4] = 10, nums2[4] = 7
→ diff = 7 - 10 = -3
→ -3 % 3 == 0 (Valid)
→ -1 operation needed → increase = 4, decrease = 2 - Index 5:
→ nums1[5] = 7, nums2[5] = 10
→ diff = 10 - 7 = 3
→ 3 % 3 == 0 (Valid)
→ +1 operation needed → increase = 5, decrease = 2
Final Calculation
- Total increase operations needed: 5
- Total decrease operations needed: 5
- Since increase == decrease, transformation is possible.
Final Output: 5
Minimum Operations to Make Array Equal II Solution
Now let's checkout the "Minimum Operations to Make Array Equal II" code in C++, Java, Python and JavaScript.
"Minimum Operations to Make Array Equal II" Code in all Languages.
1. Minimum Operations to Make Array Equal II solution in C++ Try on Compiler
class Solution {
public:
long long minOperations(vector<int>& nums1, vector<int>& nums2, int k) {
// If k is 0, nums1 and nums2 must already be equal; otherwise, it's impossible to transform.
if (k == 0) {
return nums1 == nums2 ? 0 : -1;
}
long long increase = 0, decrease = 0;
for (int i = 0; i < nums1.size(); i++) {
// Calculate the difference required to match nums2[i]
int diff = nums2[i] - nums1[i];
// If the difference is not a multiple of k, it's impossible to transform.
if (diff % k != 0) {
return -1;
}
// Count positive changes (increments)
if (diff > 0) {
increase += diff / k;
}
// Count negative changes (decrements)
else if (diff < 0) {
decrease += -diff / k;
}
}
// If total increments equal total decrements, return the number of operations;otherwise, return -1.
return (increase == decrease) ? increase : -1;
}
};2. Minimum Operations to Make Array Equal II Solution in Java Try on Compiler
public class Solution {
public static long minOperations(int[] nums1, int[] nums2, int k) {
// If k is 0, nums1 must already be equal to nums2; otherwise, return -1.
if (k == 0) {
return Arrays.equals(nums1, nums2) ? 0 : -1;
}
long increase = 0, decrease = 0;
for (int i = 0; i < nums1.length; i++) {
// Calculate the difference required to match nums2[i]
int diff = nums2[i] - nums1[i];
// If the difference is not a multiple of k, it's impossible to transform.
if (diff % k != 0) {
return -1;
}
// Count positive changes (increments)
if (diff > 0) {
increase += diff / k;
}
// Count negative changes (decrements)
else if (diff < 0) {
decrease += -diff / k;
}
}
// If total increments equal total decrements, return the number of operations; otherwise, return -1.
return increase == decrease ? increase : -1;
}
}
3. Minimum Operations to Make Array Equal II Solution in Python Try on Compiler
class Solution:
def minOperations(self, nums1: List[int], nums2: List[int], k: int) -> int:
# If k is 0, nums1 must already be equal to nums2; otherwise, return -1.
if k == 0:
return 0 if nums1 == nums2 else -1
increase = 0
decrease = 0
for i in range(len(nums1)):
# Calculate the difference required to match nums2[i]
diff = nums2[i] - nums1[i]
# If the difference is not a multiple of k, it's impossible to transform.
if diff % k != 0:
return -1
# Count positive changes (increments)
if diff > 0:
increase += diff // k
# Count negative changes (decrements)
elif diff < 0:
decrease += -diff // k
# If total increments equal total decrements, return the number of operations; otherwise, return -1.
return increase if increase == decrease else -1
4. Minimum Operations to Make Array Equal II solution in JavaScript Try on Compiler
/**
* @param {number[]} nums1
* @param {number[]} nums2
* @param {number} k
* @return {number}
*/
var minOperations = function(nums1, nums2, k) {
// If k is 0, nums1 must already be equal to nums2; otherwise, return -1.
if (k === 0) {
return JSON.stringify(nums1) === JSON.stringify(nums2) ? 0 : -1;
}
let increase = 0, decrease = 0;
for (let i = 0; i < nums1.length; i++) {
// Calculate the difference required to match nums2[i]
let diff = nums2[i] - nums1[i];
// If the difference is not a multiple of k, it's impossible to transform.
if (diff % k !== 0) {
return -1;
}
// Count positive changes (increments)
if (diff > 0) {
increase += diff / k;
}
// Count negative changes (decrements)
else if (diff < 0) {
decrease += -diff / k;
}
}
// If total increments equal total decrements, return the number of operations; otherwise, return -1.
return increase === decrease ? increase : -1;
};Minimum Operations to Make Array Equal II Complexity Analysis
Time Complexity: O(n)
Iterating through both arrays while tracking increments and decrements:
- We traverse nums1 and nums2 once, calculating the required operations to increase or decrease values.
- If any difference is not a multiple of k, we return -1 immediately.
- This operation takes O(n) time.
Checking if total increments and decrements match:
- If the sum of required +k operations equals the sum of -k operations, the transformation is possible.
- This is a constant-time O(1) operation.
Thus, the overall time complexity is:
O(n) + O(1) = O(n), where n is the length of the arrays.
Space Complexity: O(1)
Auxiliary Space Complexity
- The algorithm only uses a few extra variables (increase, decrease, diff, k).
- No additional data structures (like lists, hash maps, or recursion stacks) are used.
- Thus, auxiliary space complexity is: O(1).
Total Space Complexity
- Input storage (arrays nums1 and nums2 of size n): O(n).
- In-place iteration: No extra arrays or lists are created.
- Constant space for variables: O(1).
Thus, the total space complexity is: O(1)
Similar Problems
You have an array arr of length n where arr[i] = (2 * i) + 1 for all valid values of i (i.e., 0 <= i < n).
In one operation, you can select two indices x and y where 0 <= x, y < n and subtract 1 from arr[x] and add 1 to arr[y] (i.e., perform arr[x] -=1 and arr[y] += 1). The goal is to make all the elements of the array equal. It is guaranteed that all the elements of the array can be made equal using some operations.
Given an integer n, the length of the array, return the minimum number of operations needed to make all the elements of arr equal.
You are given two positive integer arrays nums and target, of the same length.
In one operation, you can choose any two distinct indices i and j where 0 <= i, j < nums.length and:
- set nums[i] = nums[i] + 2 and
- set nums[j] = nums[j] - 2.
Two arrays are considered to be similar if the frequency of each element is the same.
Return the minimum number of operations required to make nums similar to target. The test cases are generated such that nums can always be similar to target.