Minimum Common Value Solution In C++/Java/Python/JS
Minimum Common Value Problem Description:
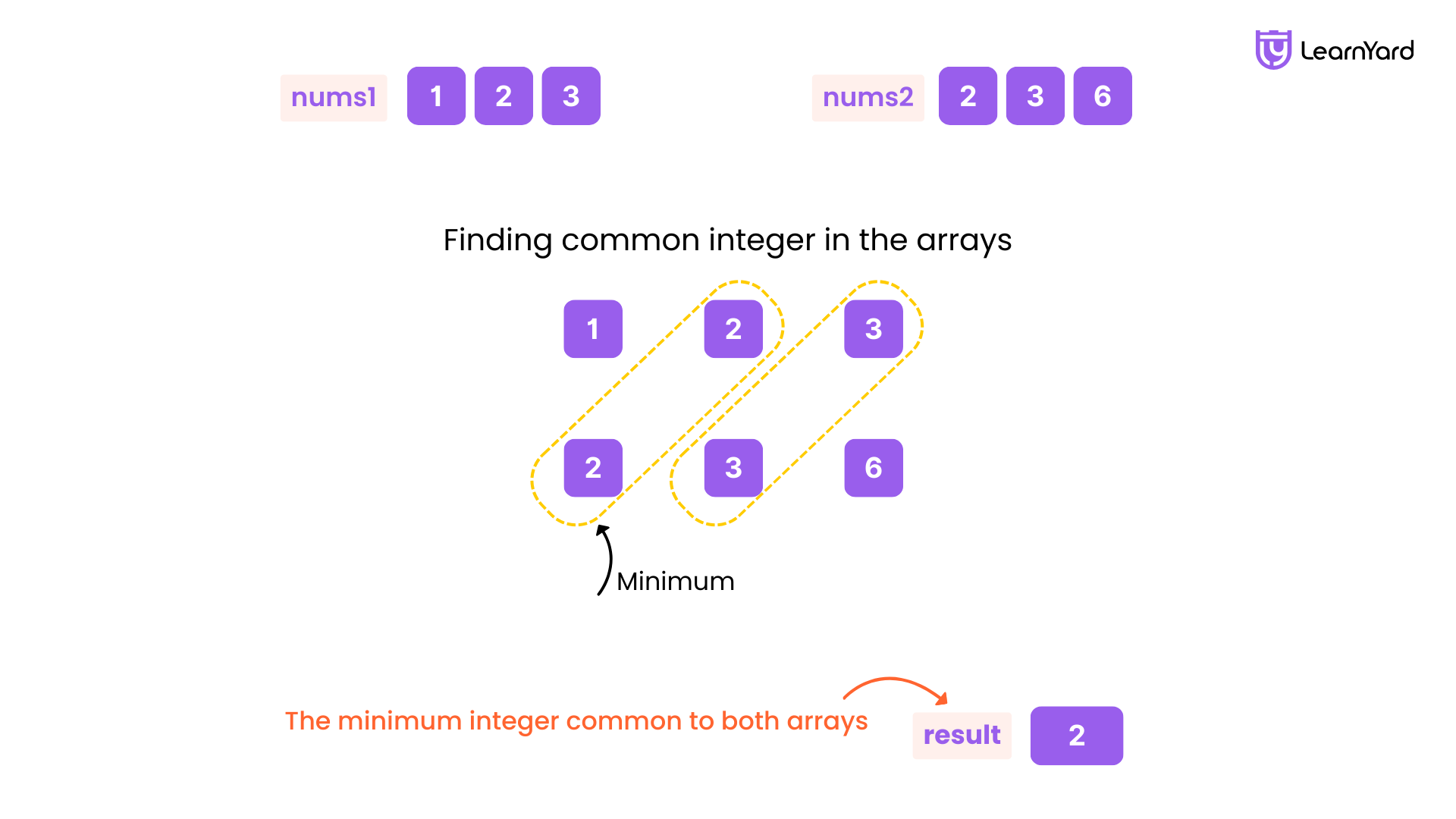
Given two integer arrays nums1 and nums2, sorted in non-decreasing order, return the minimum integer common to both arrays. If there is no common integer among nums1 and nums2, return -1.
An integer is said to be common to nums1 and nums2 if both arrays have at least one occurrence of that integer.
Examples:
Input: nums1 = [1,2,3], nums2 = [2,4]
Output: 2
Explanation: The smallest element common to both arrays is 2, so we return 2.
Input: nums1 = [1,2,3,6], nums2 = [2,3,4,5]
Output: 2
Explanation: There are two common elements in the array: 2 and 3, out of which 2 is the smallest, so 2 is returned.
Constraints:
1 ≤ nums1.length, nums2.length ≤ 10⁵
1 ≤ nums1[i], nums2[j] ≤ 10⁹
Both nums1 and nums2 are sorted in non-decreasing order.
Brute Force Approach
Ok, let's understand the problem statement.
We need to find the smallest number that appears in both nums1 and nums2. Since both arrays are sorted, this makes our task easier.
We can start iterating through nums1, and for each element, we check whether it is present in nums2. If we find a match, we immediately return that number as the smallest common element.
Function getCommon(nums1, nums2):
For each num1 in nums1:
For each num2 in nums2:
If num1 == num2:
// First common element found
Return num1
// No common element found
Return -1
For every element of nums1, we are checking every element of nums2, so it will take a time complexity of O(n * m).
But wait! We can make a slight improvement, as we have a key observation:
- The arrays are sorted
Since both nums1 and nums2 are sorted in non-decreasing order, we can take advantage of their structure. - The middle element helps minimize or maximize the search space
If we want to check whether an element num1 from nums1 is present in nums2, we don’t need to scan nums2 linearly. Instead, we can take the middle element of nums2:
1. If the middle element is greater than num1, we move left to search in the smaller half.
2. If the middle element is smaller than num1, we move right to search in the larger half.
3. If the middle element matches num1, we have found the common element and can return it immediately.
This way, we efficiently narrow down the search space instead of scanning all elements linearly. - The search space is monotonic
Because nums2 is sorted, the elements in the left half are always smaller (or equal) to those on the right.
With these conditions satisfied, we can confidently apply binary search here.
Instead of checking every element of nums1 in nums2 linearly, we can perform binary search for each element of nums1 in nums2.
Minimum Common Value Algorithm
- Iterate through nums1
- For each element num1 in nums1, check if it exists in nums2 using binary search.
- Binary search in nums2
- Perform binary search to check whether num1 is present in nums2 efficiently.
- Return the first common element
- The first element we find will be the smallest common element, so we return it immediately.
- Return -1 if no common element is found
- If no match is found after checking all elements of nums1, return -1.
This improves the time complexity to O(n log m) instead of O(n * m), making it much faster.
Let's understand with an example:
Minimum Common Value Example:
Input:
nums1 = [2, 3, 5, 6, 9, 10, 12]
nums2 = [1, 4, 7, 8, 10]
Step 1: Iterate Through nums1 and Perform Binary Search in nums2
- Check 2 in nums2 using Binary Search:
- Middle element = 7 (nums2[2])
- Since 7 > 2, move left
- Middle element = 4 (nums2[1])
- Since 4 > 2, move left
- Middle element = 1 (nums2[0])
- Since 1 < 2, move right → Not Found
- Check 3 in nums2 using Binary Search:
- Middle element = 7
- Since 7 > 3, move left
- Middle element = 4
- Since 4 > 3, move left
- Middle element = 1
- Since 1 < 3, move right → Not Found
- Check 5 in nums2 using Binary Search:
- Middle element = 7
- Since 7 > 5, move left
- Middle element = 4
- Since 4 < 5, move right → Not Found
- Check 6 in nums2 using Binary Search:
- Middle element = 7
- Since 7 > 6, move left
- Middle element = 4
- Since 4 < 6, move right → Not Found
- Check 9 in nums2 using Binary Search:
- Middle element = 7
- Since 7 < 9, move right
- Middle element = 8
- Since 8 < 9, move right → Not Found
- Check 10 in nums2 using Binary Search:
- Middle element = 7
- Since 7 < 10, move right
- Middle element = 8
- Since 8 < 10, move right
- Middle element = 10 → Found!
Step 2: Return First Common Element
- The first common element found is 10, so we return 10.
Final Output: 10
Steps to Implement the Solution:
- Implement a Binary Search Function
- Initialize left = 0 and right = nums2.size() - 1.
- Use a while loop to search for the target in nums2.
- If nums2[mid] == target, return true.
- If nums2[mid] > target, search in the left half.
- Otherwise, search in the right half.
- If the element is not found, return false.
- Iterate Through nums1
- For each num in nums1, call binarySearch(nums2, num).
- If found, return num (smallest common element).
- Return -1 If No Common Element Exists
- If no match is found after checking all elements, return -1.
Minimum Common Value Leetcode Solution
Minimum Common Value Leetcode Solution / Code Implementation
1. Minimum Common Value solution in C++ Try on Compiler
class Solution {
// Function to perform binary search in nums2
bool binarySearch(vector<int>& nums2, int target) {
// Initialize the left and right pointers for binary search
int left = 0, right = nums2.size() - 1;
// Perform binary search
while (left <= right) {
// Calculate the middle index
int mid = left + (right - left) / 2;
// Check if the middle element matches the target
if (nums2[mid] == target) {
return true;
}
// If the middle element is greater, search in the left half
if (nums2[mid] > target) {
right = mid - 1;
}
// Otherwise, search in the right half
else {
left = mid + 1;
}
}
// Target not found in nums2
return false;
}
public:
// Function to find the smallest common element between two sorted arrays
int getCommon(vector<int>& nums1, vector<int>& nums2) {
// Iterate through each element in nums1
for (int num : nums1) {
// Perform binary search in nums2 for the current num
if (binarySearch(nums2, num)) {
return num; // Return the first common element found
}
}
// No common element found, return -1
return -1;
}
};
2. Minimum Common Value solution in Java Try on Compiler
class Solution {
// Function to perform binary search in nums2
private boolean binarySearch(int[] nums2, int target) {
// Initialize left and right pointers
int left = 0, right = nums2.length - 1;
// Perform binary search
while (left <= right) {
// Calculate the middle index
int mid = left + (right - left) / 2;
// Check if the middle element matches the target
if (nums2[mid] == target) {
return true;
}
// If the middle element is greater, search in the left half
if (nums2[mid] > target) {
right = mid - 1;
}
// Otherwise, search in the right half
else {
left = mid + 1;
}
}
// Target not found in nums2
return false;
}
// Function to find the smallest common element between two sorted arrays
public int getCommon(int[] nums1, int[] nums2) {
// Iterate through each element in nums1
for (int num : nums1) {
// Perform binary search in nums2 for the current num
if (binarySearch(nums2, num)) {
return num; // Return the first common element found
}
}
// No common element found, return -1
return -1;
}
}
3. Minimum Common Value solution in Python Try on Compiler
class Solution:
# Function to perform binary search in nums2
def binarySearch(self, nums2, target):
# Initialize left and right pointers
left, right = 0, len(nums2) - 1
# Perform binary search
while left <= right:
# Calculate the middle index
mid = left + (right - left) // 2
# Check if the middle element matches the target
if nums2[mid] == target:
return True
# If the middle element is greater, search in the left half
if nums2[mid] > target:
right = mid - 1
# Otherwise, search in the right half
else:
left = mid + 1
# Target not found in nums2
return False
# Function to find the smallest common element between two sorted arrays
def getCommon(self, nums1, nums2):
# Iterate through each element in nums1
for num in nums1:
# Perform binary search in nums2 for the current num
if self.binarySearch(nums2, num):
# Return the first common element found
return num
# No common element found, return -1
return -1
4. Minimum Common Value solution in Javascript Try on Compiler
/**
* Function to find the smallest common element in two sorted arrays
* @param {number[]} nums1 - First sorted array
* @param {number[]} nums2 - Second sorted array
* @return {number} - Smallest common element or -1 if no common element exists
*/
var getCommon = function(nums1, nums2) {
// Function to perform binary search in nums2
function binarySearch(nums2, target) {
// Initialize left and right pointers
let left = 0, right = nums2.length - 1;
// Perform binary search
while (left <= right) {
// Calculate the middle index
let mid = Math.floor(left + (right - left) / 2);
// Check if the middle element matches the target
if (nums2[mid] === target) {
return true;
}
// If the middle element is greater, search in the left half
if (nums2[mid] > target) {
right = mid - 1;
}
// Otherwise, search in the right half
else {
left = mid + 1;
}
}
// Target not found in nums2
return false;
}
// Iterate through each element in nums1
for (let num of nums1) {
// Perform binary search in nums2 for the current num
if (binarySearch(nums2, num)) {
return num; // Return the first common element found
}
}
// No common element found, return -1
return -1;
};
Minimum Common Value Complexity Analysis (Brute Force)
Time Complexity: O(n log m)
Let n be the size of nums1 and m be the size of nums2.
- Binary Search Complexity:
- The binarySearch function is called for each element in nums1.
- Each binary search operation takes O(log m) time since it performs a logarithmic search in nums2.
- Looping Through nums1:
- We iterate through all n elements of nums1, calling binarySearch on each.
Overall Complexity Calculation
- Each binary search takes O(log m).
- We perform binary search for every element in nums1, so the total complexity is: O(n log m)
Space Complexity: O(m+n)
- Auxiliary Space Complexity: O(1)
The algorithm only uses a few integer variables such as left, right, mid, and loop counters.
Therefore, the auxiliary space complexity is O(1). - Total Space Complexity: O(m+n)
We only use the given input arrays nums1 and nums2, and we do not duplicate them.
Therefore, the total space complexity is O(m+n).
Will Brute Force Work Against the Given Constraints?
For the current solution, the time complexity is O(n log m), where n is the number of elements in nums1 (1 ≤ nums1.length ≤ 10⁵) and m is the number of elements in nums2 (1 ≤ nums2.length ≤ 10⁵).
- In the worst-case scenario, we iterate through all elements of nums1 (O(n)), and for each element, we perform a binary search on nums2 (O(log m)).
- This results in a total time complexity of O(n log m).
This can become inefficient if n is close to 10⁵ and m is also close to 10⁵, as log(10⁵) is approximately 17, leading to around 1.7 × 10⁶ operations.
However, this is significantly better than O(n × m) = 10¹⁰, making it much more practical and efficient for large inputs.
Given the constraints, where 1 ≤ nums1[i], nums2[j] ≤ 10⁹, the solution performs efficiently since binary search reduces the number of comparisons drastically.
While it may not be the absolute best solution for all cases, it ensures efficient execution for typical inputs within the given constraints.
Can we optimize it?
As we traverse nums1, we go from smallest to largest element, which means that as we move through nums1, we are always encountering increasing values in sorted order.
One thing we can observe is that if we find an element from nums1 that is also present in nums2, that element is the smallest common element because we are traversing nums1 in sorted order. This means that as soon as we find a match, we can immediately return that element as our answer.
But how can we efficiently check if an element from nums1 exists in nums2?
We can use a hashset to quickly check if an element is present.
What is a hashset?
A hashset is a data structure that stores key-value pairs and allows for fast lookups, insertions, and deletions in O(1) average time complexity.
The idea is simple:
First, we store every element of nums2 in a hash set because checking for the existence of an element in a set takes O(1) time on average.
Then, we iterate through nums1, and for each element, we check if it exists in the hash set.
The first such element we find is the smallest common element, so we return it immediately.
If we go through all elements in nums1 without finding any match, that means no common element exists, so we return -1.
Let us understand this approach by a video,
Minimum Common Value-Optimal-Approach-Animation
Let's understand with an example:
Minimum Common Value Example:
nums1 = [2, 3, 5, 6, 9, 10, 12]
nums2 = [1, 4, 7, 8, 10]
Step 1: Store nums2 in a Hash Set
We create a hash set and store all elements of nums2 for quick lookups.
The hash set will contain entries for: 1, 4, 7, 8, and 10.
Step 2: Traverse nums1 and Check for Common Elements
- Check 2 → Not in the hash set.
- Check 3 → Not in the hash set.
- Check 5 → Not in the hash set.
- Check 6 → Not in the hash set.
- Check 9 → Not in the hash set.
- Check 10 → Found in the hash set!
Step 3: Return the Result
Since 10 is the first common element, we return 10 as the smallest common integer.
Final Output: 10
Steps to Implement the Solution:
- Create a hash set to store all elements of nums2.
- Insert all elements of nums2 into the hash set for quick lookups.
- Traverse nums1 and check if any element exists in the hash set.
- If a match is found, return the element immediately (smallest common element).
- If no match is found, return -1 (no common element).
Minimum Common Value Leetcode Solution
Minimum Common Value Leetcode Solution / Code Implementation
1. Minimum Common Value solution in C++ Try on Compiler
class Solution {
public:
int getCommon(vector<int>& nums1, vector<int>& nums2) {
// Create an unordered set to store elements of nums2
unordered_set<int> hashset;
// Insert all elements of nums2 into the hash set
for(auto &num: nums2)
hashset.insert(num);
// Traverse nums1 and check for the first common element
for(auto &num: nums1)
{
// If the current element exists in the hash set, return it as the smallest common element
if(hashset.count(num))
return num;
}
// If no common element is found, return -1
return -1;
}
};
2. Minimum Common Value solution in Java Try on Compiler
import java.util.HashSet;
class Solution {
public int getCommon(int[] nums1, int[] nums2) {
// Create a HashSet to store elements of nums2
HashSet<Integer> hashSet = new HashSet<>();
// Insert all elements of nums2 into the hash set
for (int num : nums2) {
hashSet.add(num);
}
// Traverse nums1 and check for the first common element
for (int num : nums1) {
// If the current element exists in the hash set, return it as the smallest common element
if (hashSet.contains(num)) {
return num;
}
}
// If no common element is found, return -1
return -1;
}
}
3. Minimum Common Value solution in Python Try on Compiler
class Solution:
def getCommon(self, nums1, nums2):
# Create a hash set to store elements of nums2
hash_set = set(nums2)
# Traverse nums1 and check for the first common element
for num in nums1:
# If the current element exists in the hash set, return it as the smallest common element
if num in hash_set:
return num
# If no common element is found, return -1
return -1
4. Minimum Common Value solution in Javascript Try on Compiler
/**
* @param {number[]} nums1
* @param {number[]} nums2
* @return {number}
*/
var getCommon = function (nums1, nums2) {
// Create a Set to store elements of nums2
let hashSet = new Set(nums2);
// Traverse nums1 and check for the first common element
for (let num of nums1) {
// If the current element exists in the Set, return it as the smallest common element
if (hashSet.has(num)) {
return num;
}
}
// If no common element is found, return -1
return -1;
};Minimum Common Value Complexity Analysis (Hashset)
Time Complexity: O(n + m)
The approach consists of two main steps:
- Inserting elements of nums2 into a hash set
- We iterate through nums2 and insert each element into the hash set.
- Time Complexity: O(m) (where m is the length of nums2).
- Reason: Insertion in a hash set takes O(1) on average, so inserting m elements takes O(m).
- Traversing nums1 and checking for the first common element
- We iterate through nums1 and check if each element exists in the hash set.
- Time Complexity: O(n) (where n is the length of nums1).
- Reason: Checking existence in a hash set takes O(1) on average, so checking n elements takes O(n).
Overall Time Complexity
- O(m) + O(n) = O(n + m)
- This is optimal for this problem because we only scan both arrays once and use efficient O(1) lookups in a hash set.
Space Complexity: O(n+m)
- Auxiliary Space Complexity: O(1)
The algorithm only uses a few integer variables like loop counters and temporary variables, which are primitive types that occupy O(1) space.
Therefore, the auxiliary space complexity is O(1). - Total Space Complexity: O(n+m)
We create a hash set to store all elements of nums2, which requires O(m) space (where m is the length of nums2).
We do not use any additional data structures apart from this hash set.
Since nums1 and nums2 are given as input and not duplicated, they do not contribute to extra space usage.
Therefore, the total space complexity is O(n+m).
Can there be another approach?
Yes! There is one more approach that is slightly more efficient than the previous one.
In the brute force approach, we searched for every element of nums1 in nums2. For each element, we scanned the entire nums2, making the approach inefficient with a time complexity of O(n × m).
But wait—there’s a catch!
Both arrays are sorted!!
This means that if we have an element num1 from nums1 and we are searching for it in nums2, as soon as we encounter a number greater than num1 in nums2, we can immediately stop.
Why?
Because nums2 is sorted, and all the numbers after this greater number will be even larger, meaning num1 can never be found beyond this point.
So instead of scanning the entire nums2, we simply increase the counter of nums1 and move to the next number, repeating the same process.
Yes! This approach is known as the Two-Pointer Technique because we use two pointers—one for nums1 and one for nums2—to efficiently find the smallest common element.
Minimum Common Value Algorithm
- One pointer starts at the beginning of nums1
- The other pointer starts at the beginning of nums2
- We move the pointers forward based on comparisons:
- If nums1[i] is smaller, move the nums1 pointer forward.
- If nums2[j] is smaller, move the nums2 pointer forward.
- If both are equal, we have found the smallest common element, so we return it immediately.
Since we are only traversing both arrays once, the time complexity is O(n + m), which is very efficient compared to O(n × m) in brute force.
let us understand this approch through a video,
Minimum Common Value-Optimal-Approach-Annimation-2
Let's understand with an example:
Minimum Common Value Example:
Concise Dry Run (Two-Pointer Approach)
Input:
nums1 = [2, 3, 5, 6, 9, 10, 12]
nums2 = [1, 4, 7, 8, 10]
Step-by-step Execution:
- Pointers start at the beginning:
- nums1[0] = 2, nums2[0] = 1
- 1 < 2, move nums2 pointer → (j = 1)
- Compare again:
- nums1[0] = 2, nums2[1] = 4
- 2 < 4, move nums1 pointer → (i = 1)
- Compare again:
- nums1[1] = 3, nums2[1] = 4
- 3 < 4, move nums1 pointer → (i = 2)
- Compare again:
- nums1[2] = 5, nums2[1] = 4
- 4 < 5, move nums2 pointer → (j = 2)
- Compare again:
- nums1[2] = 5, nums2[2] = 7
- 5 < 7, move nums1 pointer → (i = 3)
- Compare again:
- nums1[3] = 6, nums2[2] = 7
- 6 < 7, move nums1 pointer → (i = 4)
- Compare again:
- nums1[4] = 9, nums2[2] = 7
- 7 < 9, move nums2 pointer → (j = 3)
- Compare again:
- nums1[4] = 9, nums2[3] = 8
- 8 < 9, move nums2 pointer → (j = 4)
- Compare again:
- nums1[4] = 9, nums2[4] = 10
- 9 < 10, move nums1 pointer → (i = 5)
- Compare again:
- nums1[5] = 10, nums2[4] = 10
- Both are equal! Return 10
Final Output: 10
How to code it up:
- Initialize Two Pointers
- Start with two indices i = 0 and j = 0 to traverse nums1 and nums2.
- Traverse Both Arrays Simultaneously
- Use a while loop to iterate until we reach the end of either array.
- Check for Common Elements
- If nums1[i] == nums2[j], return nums1[i] as the smallest common element.
- Move the Pointers
- If nums1[i] < nums2[j], move pointer i forward.
- Otherwise, move pointer j forward.
- Return -1 If No Common Element Exists
- If the loop completes without finding a match, return -1.
Minimum Common Value Leetcode Solution
Minimum Common Value Leetcode Solution / Code Implementation
1. Minimum Common Value solution in C++ Try on Compiler
class Solution {
public:
int getCommon(vector<int>& nums1, vector<int>& nums2) {
// Initialize two pointers to traverse nums1 and nums2
int i = 0, j = 0;
// Traverse both arrays until we reach the end of either
while (i < nums1.size() && j < nums2.size()) {
// If the elements at both pointers are equal, return the common element
if (nums1[i] == nums2[j])
return nums1[i];
// If nums1[i] is smaller, move the pointer i forward
else if (nums1[i] < nums2[j])
i++;
// Otherwise, move the pointer j forward
else
j++;
}
// If no common element is found, return -1
return -1;
}
};
2. Minimum Common Value solution in Java Try on Compiler
class Solution {
public int getCommon(int[] nums1, int[] nums2) {
// Initialize two pointers to traverse nums1 and nums2
int i = 0, j = 0;
// Traverse both arrays until we reach the end of either
while (i < nums1.length && j < nums2.length) {
// If the elements at both pointers are equal, return the common element
if (nums1[i] == nums2[j])
return nums1[i];
// If nums1[i] is smaller, move the pointer i forward
else if (nums1[i] < nums2[j])
i++;
// Otherwise, move the pointer j forward
else
j++;
}
// If no common element is found, return -1
return -1;
}
}
3. Minimum Common Value solution in Python Try on Compiler
class Solution:
def getCommon(self, nums1, nums2):
# Initialize two pointers to traverse nums1 and nums2
i, j = 0, 0
# Traverse both arrays until we reach the end of either
while i < len(nums1) and j < len(nums2):
# If the elements at both pointers are equal, return the common element
if nums1[i] == nums2[j]:
return nums1[i]
# If nums1[i] is smaller, move the pointer i forward
elif nums1[i] < nums2[j]:
i += 1
# Otherwise, move the pointer j forward
else:
j += 1
# If no common element is found, return -1
return -1
4. Minimum Common Value solution in Javascript Try on Compiler
var getCommon = function(nums1, nums2) {
// Initialize two pointers to traverse nums1 and nums2
let i = 0, j = 0;
// Traverse both arrays until we reach the end of either
while (i < nums1.length && j < nums2.length) {
// If the elements at both pointers are equal, return the common element
if (nums1[i] === nums2[j])
return nums1[i];
// If nums1[i] is smaller, move the pointer i forward
else if (nums1[i] < nums2[j])
i++;
// Otherwise, move the pointer j forward
else
j++;
}
// If no common element is found, return -1
return -1;
};
Minimum Common Value Complexity Analysis (Two Pointers)
Time Complexity: O(n + m)
Step 1: Traversing the Arrays
- We have two sorted arrays: nums1 of size n and nums2 of size m.
- We use two pointers i and j, which traverse nums1 and nums2, respectively.
- At each step, we compare nums1[i] and nums2[j]:
- If they are equal, we return the element.
- If nums1[i] is smaller, we increment i to find a match.
- If nums2[j] is smaller, we increment j to find a match.
Step 2: Number of Operations
- Each element from nums1 and nums2 is visited at most once.
- In the worst case, both i and j will traverse their respective arrays fully.
- This results in n + m total comparisons.
Final Time Complexity
- Since we process each element only once, the time complexity is O(n + m).
Space Complexity: O(n+m)
- Auxiliary Space Complexity: O(1)
The algorithm only uses a few integer variables: i, j (pointers for traversal).
Therefore, the auxiliary space complexity is O(1). - Total Space Complexity: O(n + m)
Since we have two arrays nums1 and nums2, of size n and m, respectively.
Therefore, the total space complexity is O(n + m)
Similar Problems
Finding the minimum value in an array can be approached in various ways, depending on the problem constraints. If the array is unsorted, using a Hash Table can help in storing and quickly retrieving minimum values when combined with additional conditions. The Two Pointers technique is useful when working with sorted arrays or when searching for a minimum difference between two elements efficiently. If the array is sorted, Binary Search can be applied to quickly locate the minimum value under certain constraints, such as finding the smallest element greater than a given number. By combining these techniques, we can efficiently determine the minimum value based on the problem's requirements.
Now that we have successfully tackled this problem, let's try these similar problems.
Given two integer arrays nums1 and nums2, return an array of their intersection. Each element in the result must be unique and you may return the result in any order.
Given two integer arrays nums1 and nums2, return an array of their intersection. Each element in the result must appear as many times as it shows in both arrays and you may return the result in any order.