Minimize Maximum of Array Solution In C++/Java/Python/JS
Problem Description
You are given a 0-indexed array nums comprising of n non-negative integers.
In one operation, you must:
Choose an integer i such that 1 <= i < n and nums[i] > 0.
Decrease nums[i] by 1.
Increase nums[i - 1] by 1.
Return the minimum possible value of the maximum integer of nums after performing any number of operations.
Example
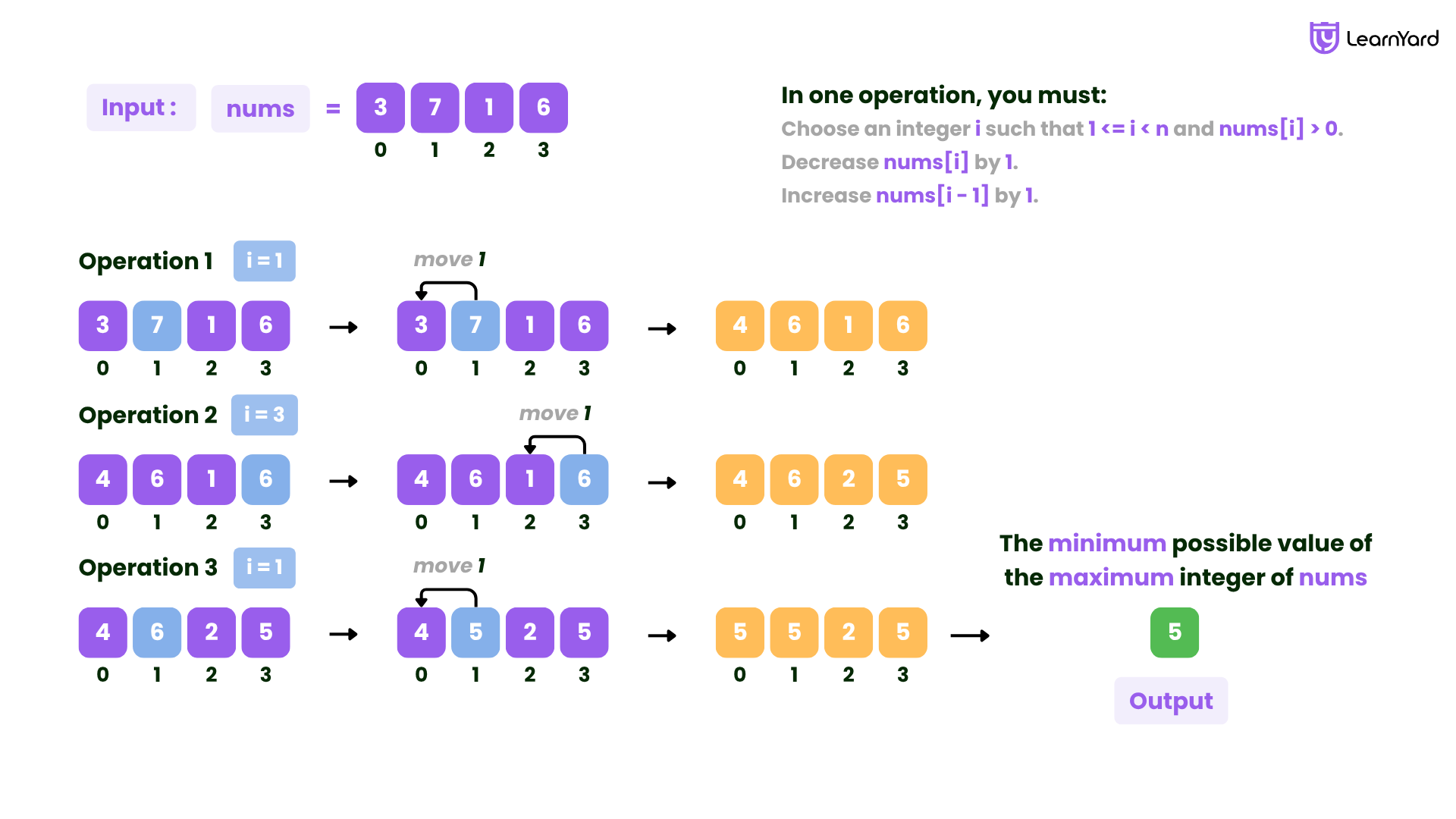
Input: nums = [3,7,1,6]
Output: 5
Explanation:
One set of optimal operations is as follows:
1. Choose i = 1, and nums becomes [4,6,1,6].
2. Choose i = 3, and nums becomes [4,6,2,5].
3. Choose i = 1, and nums becomes [5,5,2,5].
The maximum integer of nums is 5. It can be shown that the maximum number cannot be less than 5.
Therefore, we return 5.
Input: nums = [10,1]
Output: 10
Explanation:
It is optimal to leave nums as is, and since 10 is the maximum value, we return 10.
Constraints
- n == nums.length
- 2 <= n <= 105
- 0 <= nums[i] <= 109
Figuring out "Minimize Maximum of Array solution" can be solved using different approaches. We will first figure out the most intuitive approach and move to the optimal approach if exists. Let's sit with a pen and paper and figure out the algorithm !!
Optimal Approach
Intuition
We are given an array of non-negative integers, and we can perform an operation where we take a value from an index i (as long as i > 0 and nums[i] > 0) and move it to index i-1. Our goal is to minimize the maximum value in the array after performing any number of these operations.
Let’s start by understanding this with a small example. Suppose we have:
nums = [2, 10, 3, 1]
What do you think is the issue with this array?
Well, the second element nums[1] = 10 is pretty large compared to the rest. If our goal is to minimize the maximum value, we might want to reduce this 10 somehow.
Exactly! We should aim to "distribute" this large value somewhere else. But here’s the catch—our operation only allows moving values to the left.
Now, let’s step back and think:
If we could move values both left and right, we would be able to balance things out perfectly.
In that case, an intuitive strategy would be to evenly distribute the total sum of the array across all elements.
2 + 10 + 3 + 1 = 16
If we could distribute freely, the ideal balanced value would be: 16 / 4 = 4
So in a perfect world where we can move values anywhere, we could potentially get an array like [4, 4, 4, 4].
That makes sense! But since we can only move values to the left, does that mean we won’t always reach this ideal balanced value? Exactly. Because we can’t move values to the right, we need to be cautious about how we distribute values.
So can we say that as we move from left to right, we can maintain a running sum and ask:
"If we could distribute this sum across all elements seen so far, what would be the maximum value at this point?"
First element (nums[0] = 2):
The prefix sum so far is 2. Since we’ve seen only 1 element, the minimum possible max value is: ceil(2 / 1) = 2 .So, the answer so far is 2.
Second element (nums[1] = 10):
The new prefix sum is 2 + 10 = 12.
We now have 2 elements, so the possible max value is: ceil(12 / 2) = 6
We update our answer to max(2, 6) = 6.
Third element (nums[2] = 3):
The new prefix sum is 12 + 3 = 15.
We now have 3 elements, so the possible max value is: ceil(15 / 3) = 5
We update our answer to max(6, 5) = 6.
Fourth element (nums[3] = 1):
The new prefix sum is 15 + 1 = 16. We now have 4 elements, so the possible max value is: ceil(16 / 4) = 4
We update our answer to max(6, 4) = 6.
Wait… shouldn't the final answer be 4 since that’s the last computed value?
But we must remember, we are only allowed to move values to the left, so we can’t reduce the max value once it has already reached a peak.
For example, when we reached index 1, we saw that the max value had to be at least 6. Even though the later values could theoretically lower it, our constraints prevent that from happening.
That’s why we always take the maximum encountered value across all steps: Final answer = 6
I see! So even though at the last step we got a value of 4, we had already seen 6 before, and since we can’t redistribute values backward, we are stuck with 6.
Now we need to step back, let’s take a step back and ask ourselves—what strategy did we use here?
We processed the array from left to right, maintaining a running sum and updating the answer based on the maximum possible value at each step. That sounds like a greedy approach!
This is indeed a greedy strategy because at each step, we made the best possible decision by ensuring we never underestimated the minimum possible maximum value.
Let's now see how our algorithm looks like!!
Minimize Maximum of Array Algorithm
- Maintain a prefix sum as we iterate through the array.
- At each step, compute the maximum possible value if we evenly distribute this sum across all seen elements.
- Update the answer as max(answer, ceil(prefixSum / (i + 1))) since the max value can never decrease due to our constraints.
- The final answer is the largest encountered value during our iteration.
That makes a lot of sense! But how to code up this approach?
Approach
Initialize Tracking Variables:
- Maintain a runningSum, which keeps track of the sum of elements processed so far.
- Maintain a minMaxValue, which stores the minimum possible maximum value encountered.
Iterate Through the Array:
- Traverse the array from left to right.
- At each step, update the runningSum by adding the current element.
- Compute the potential maximum value if we were to evenly distribute the sum across all elements seen so far:
potentialMax=[runningSum / elements seen so far] - Update minMaxValue as the maximum of its current value and potentialMax.
Return the Final Result: The computed minMaxValue at the end of iteration represents the minimized maximum value achievable given the constraints.
Let us understand this with a video,
Dry-Run
Input:- nums = [3, 1, 10, 1, 2]
Output:- 5
Step-by-Step Dry Run:
Initialization:
runningSum = 0
minMaxValue = 0
Iteration 1 (i = 0, nums[i] = 3):
runningSum = runningSum + nums[0] = 0 + 3 = 3
potentialMax = (runningSum + i) / (i + 1) = (3 + 0) / (1) = 3
minMaxValue = max(0, 3) = 3
Iteration 2 (i = 1, nums[i] = 1):
runningSum = runningSum + nums[1] = 3 + 1 = 4
potentialMax = (4 + 1) / 2 = 5 / 2 = 2
minMaxValue = max(3, 2) = 3
Iteration 3 (i = 2, nums[i] = 10):
runningSum = runningSum + nums[2] = 4 + 10 = 14
potentialMax = (14 + 2) / 3 = 16 / 3 = 5
minMaxValue = max(3, 5) = 5
Iteration 4 (i = 3, nums[i] = 1):
runningSum = runningSum + nums[3] = 14 + 1 = 15
potentialMax = (15 + 3) / 4 = 18 / 4 = 4
minMaxValue = max(5, 4) = 5
Iteration 5 (i = 4, nums[i] = 2):
runningSum = runningSum + nums[4] = 15 + 2 = 17
potentialMax = (17 + 4) / 5 = 21 / 5 = 4
minMaxValue = max(5, 4) = 5
Final Output: 5
Minimize Maximum of Array Solution
Now, let's checkout the Minimize Maximum of Array in c++, Java, Python and JavaScript
"Minimize Maximum of Array" Code in all Languages.
1. Minimize Maximum of Array solution in C++ Try on Compiler
class Solution {
public:
int minimizeArrayValue(vector<int>& nums) {
// Variable to store the running sum of elements
long long runningSum = 0;
// Variable to store the minimum possible maximum value
long long minMaxValue = 0;
// Iterate through the array
for (int i = 0; i < nums.size(); i++) {
// Add the current element to the running sum
runningSum += nums[i];
// Compute the potential maximum value using ceiling division
long long potentialMax = (runningSum + i) / (i + 1);
// Update minMaxValue with the maximum of itself and potentialMax
minMaxValue = max(minMaxValue, potentialMax);
}
// Return the computed minimum maximum value
return (int)minMaxValue;
}
};
2. Minimize Maximum of Array Solution in Java Try on Compiler
class Solution {
public int minimizeArrayValue(int[] nums) {
// Variable to store the running sum of elements
long runningSum = 0;
// Variable to store the minimum possible maximum value
long minMaxValue = 0;
// Iterate through the array
for (int i = 0; i < nums.length; i++) {
// Add the current element to the running sum
runningSum += nums[i];
// Compute the potential maximum value using ceiling division
long potentialMax = (runningSum + i) / (i + 1);
// Update minMaxValue with the maximum of itself and potentialMax
minMaxValue = Math.max(minMaxValue, potentialMax);
}
// Return the computed minimum maximum value
return (int) minMaxValue;
}
}3. Minimize Maximum of Array Solution in Python Try on Compiler
class Solution:
def minimizeArrayValue(self, nums):
# Variable to store the running sum of elements
running_sum = 0
# Variable to store the minimum possible maximum value
min_max_value = 0
# Iterate through the array
for i in range(len(nums)):
# Add the current element to the running sum
running_sum += nums[i]
# Compute the potential maximum value using ceiling division
potential_max = (running_sum + i) // (i + 1)
# Update min_max_value with the maximum of itself and potential_max
min_max_value = max(min_max_value, potential_max)
# Return the computed minimum maximum value
return min_max_value
4. Minimize Maximum of Array solution in JavaScript Try on Compiler
class Solution {
minimizeArrayValue(nums) {
// Variable to store the running sum of elements
let runningSum = 0;
// Variable to store the minimum possible maximum value
let minMaxValue = 0;
// Iterate through the array
for (let i = 0; i < nums.length; i++) {
// Add the current element to the running sum
runningSum += nums[i];
// Compute the potential maximum value using ceiling division
let potentialMax = Math.floor((runningSum + i) / (i + 1));
// Update minMaxValue with the maximum of itself and potentialMax
minMaxValue = Math.max(minMaxValue, potentialMax);
}
// Return the computed minimum maximum value
return minMaxValue;
}
}Minimize Maximum of Array Complexity Analysis
Time Complexity: O(n)
Each iteration involves constant time operations (O(1)).
Since the loop runs n times (where n = nums.size()), the overall time complexity is: O(n)
Space Complexity: O(1)
Auxiliary space refers to the extra space used excluding the input storage.
The function only uses a few long long variables (runningSum, minMaxValue, potentialMax), which are O(1).
No additional data structures are created apart from the input array.
Thus, auxiliary space complexity is: O(1)
Total Space Complexity
Total space includes both:
Input space: nums takes O(n) space.
Auxiliary space: O(1) (as analyzed above).
Thus, the total space complexity is: O(n)
Similar Problems
A conveyor belt has packages that must be shipped from one port to another within days days.
The ith package on the conveyor belt has a weight of weights[i]. Each day, we load the ship with packages on the conveyor belt (in the order given by weights). We may not load more weight than the maximum weight capacity of the ship.
Return the least weight capacity of the ship that will result in all the packages on the conveyor belt being shipped within days days.
You are assigned to put some amount of boxes onto one truck. You are given a 2D array boxTypes, where boxTypes[i] = [numberOfBoxesi, numberOfUnitsPerBoxi]:
- numberOfBoxesi is the number of boxes of type i.
- numberOfUnitsPerBoxi is the number of units in each box of the type i.
You are also given an integer truckSize, which is the maximum number of boxes that can be put on the truck. You can choose any boxes to put on the truck as long as the number of boxes does not exceed truckSize.
Return the maximum total number of units that can be put on the truck.