Maximum Running Time of N Computers Solution In C++/Java/Python/JS
Maximum Running Time of N Computers Problem Description:
You have n computers. You are given the integer n and a 0-indexed integer array batteries where the ith battery can run a computer for batteries[i] minutes. You are interested in running all n computers simultaneously using the given batteries.
Initially, you can insert at most one battery into each computer. After that and at any integer time moment, you can remove a battery from a computer and insert another battery any number of times. The inserted battery can be a totally new battery or a battery from another computer. You may assume that the removing and inserting processes take no time.
Note that the batteries cannot be recharged.
Return the maximum number of minutes you can run all the n computers simultaneously.
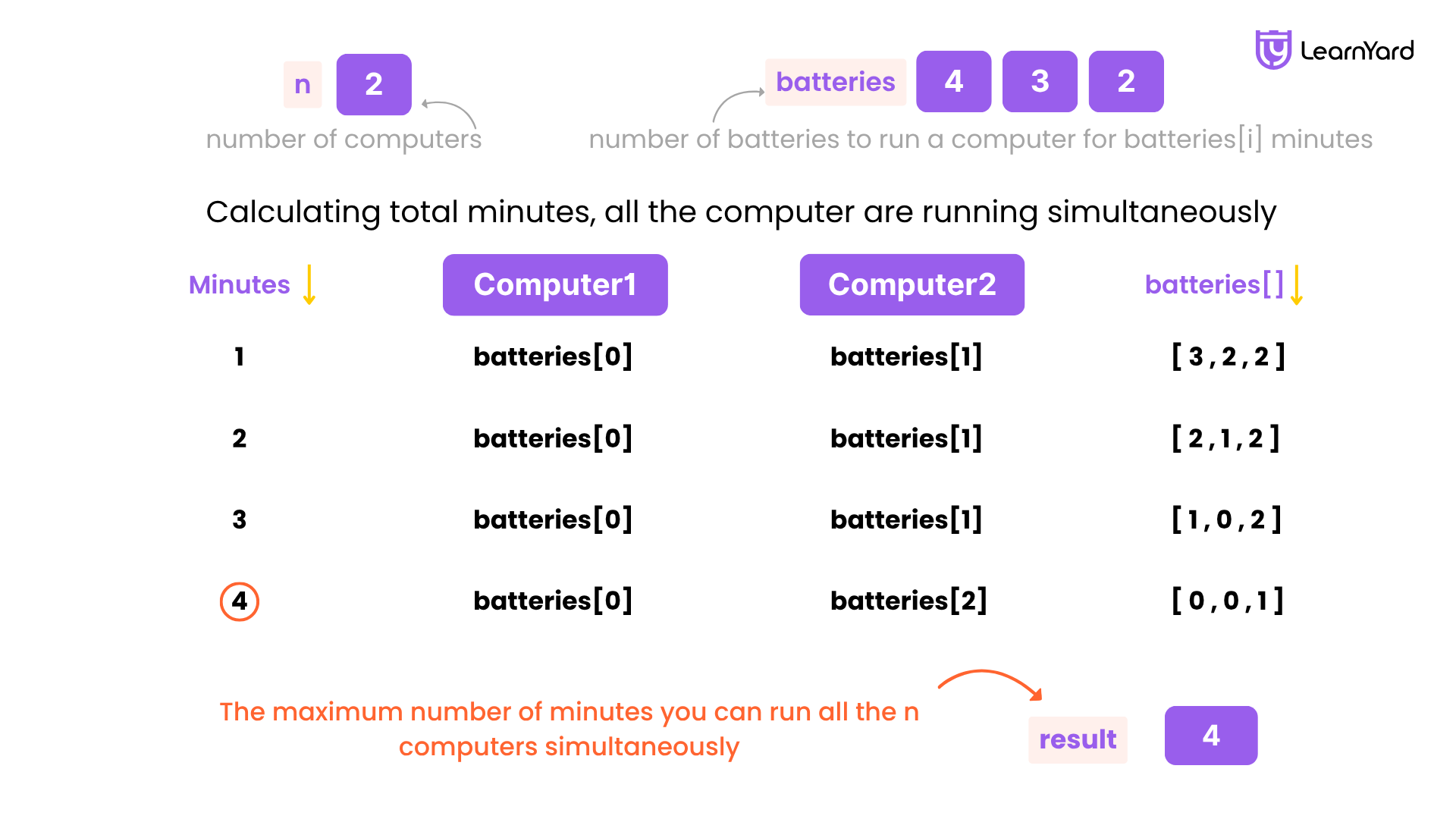
Examples:
Input: n = 2, batteries = [3,3,3]
Output: 4
Explanation:
Initially, insert battery 0 into the first computer and battery 1 into the second computer.
After two minutes, remove battery 1 from the second computer and insert battery 2 instead. Note that battery 1 can still run for one minute.
At the end of the third minute, battery 0 is drained, and you need to remove it from the first computer and insert battery 1 instead.
By the end of the fourth minute, battery 1 is also drained, and the first computer is no longer running.
We can run the two computers simultaneously for at most 4 minutes, so we return 4.
Input: n = 2, batteries = [1,1,1,1]
Output: 2
Explanation:
Initially, insert battery 0 into the first computer and battery 2 into the second computer.
After one minute, battery 0 and battery 2 are drained so you need to remove them and insert battery 1 into the first computer and battery 3 into the second computer.
After another minute, battery 1 and battery 3 are also drained so the first and second computers are no longer running.
We can run the two computers simultaneously for at most 2 minutes, so we return 2.
Constraints:
1 <= n <= batteries.length <= 10⁵
1 <= batteries[i] <= 10⁹
Brute Force Approach
To approach the problem, we are given an integer n representing the number of computers and an integer array batteries where each battery[i] represents the number of minutes it can run a computer. Our task is to determine the maximum number of minutes we can run all n computers simultaneously while ensuring that each computer is always running.
Our goal is to find the maximum number of minutes all n computers can run simultaneously by optimally using and swapping the batteries. If it is impossible to keep n computers running, we return 0.
What can be the minimum number of minutes all computers can run simultaneously?
The minimum number of minutes required should be 0 because if the total sum of battery power available is less than n, then we do not have enough power to run all computers even for a single minute, and the answer must be 0.
Now that we know the minimum number of minutes, what would be the maximum number of minutes all computers can run?
The maximum number of minutes required should be sum(batteries) // n. This is because, in the best case, if we could perfectly distribute battery power, the total power divided equally among n computers gives the longest runtime.
Thus, our search space for the answer ranges from 0 to sum(batteries) // n. Now, the problem reduces to finding the maximum number of minutes that all computers can run simultaneously while ensuring power is distributed optimally.
A basic approach is to iterate through all possible values from 0 to sum(batteries) // n and check whether it is possible to keep all n computers running for at least that many minutes.
If it is possible, then it is a valid solution. We continue this process until we find the maximum number of minutes that allow us to run all n computers. We can either start from 0 and go up to sum(batteries) // n or start from sum(batteries) // n and go down to 0.
The idea is to start from 0 to sum(batteries) // n and stop whenever we find the point where it's not possible to keep all computers running, and return the point before it as it was the maximum number of minutes we could sustain the n computers.
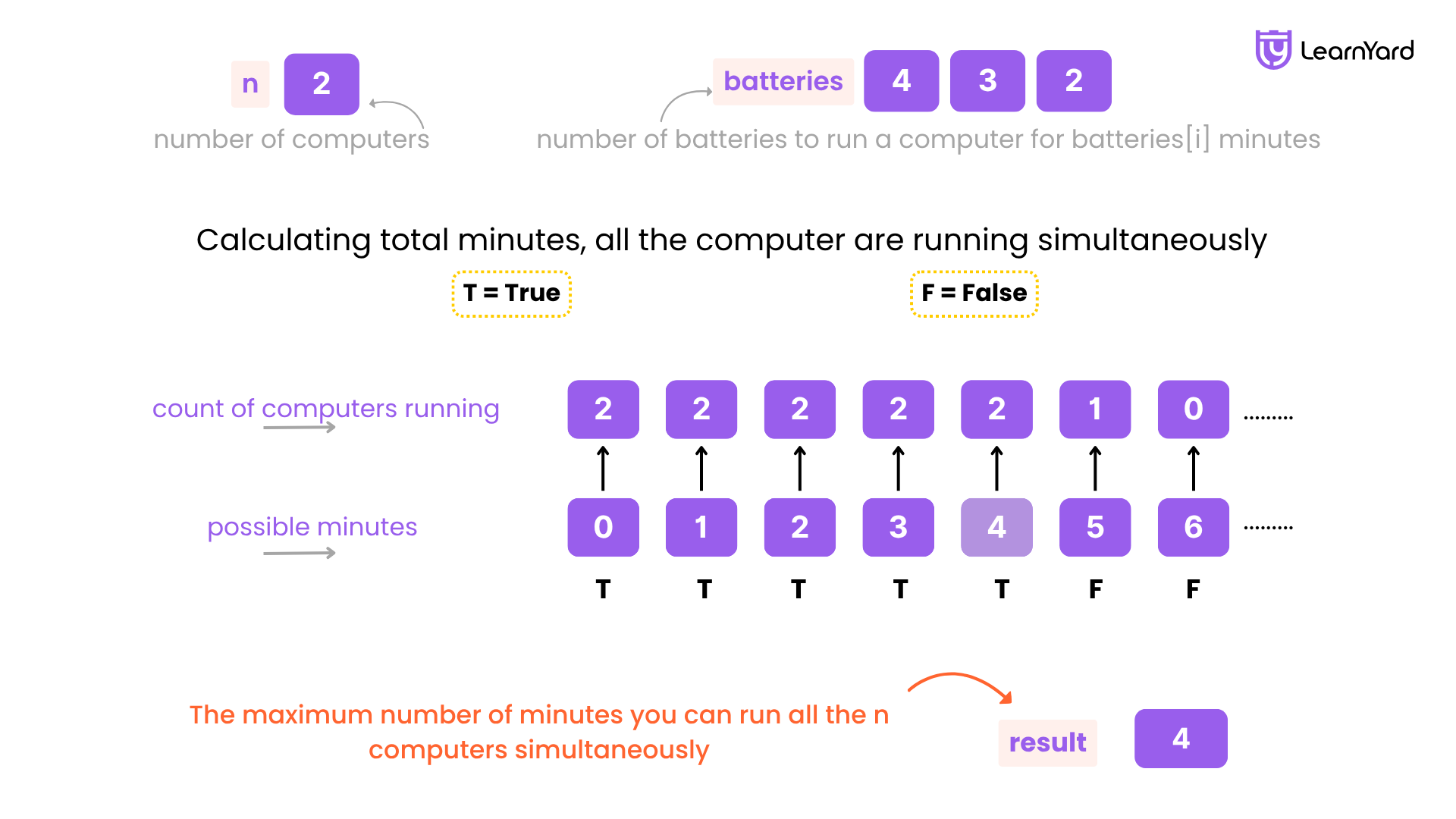
Consider n = 2 and batteries = [3,3,3]. We start by setting the smallest possible value as 0 and the largest possible value as sum(batteries) // n = (3+3+3) // 2 = 4.
We then check if it is possible to run all n computers for different values of minutes:
If we try running for 0 minutes, we can trivially run all computers, so it works. Similarly, if we try running for 1, 2, or 3 minutes, we can still manage to keep both computers running, so it will also work.
If we try running for 4 minutes, we can still swap batteries optimally and manage to run all computers.
If we try running for 5 minutes, we no longer have enough power to keep all computers running, so this does not work.
Since 5 is the first point where it's not possible to keep n computers running, we return 4, the point before it. Thus, the answer is 4.
We can see that every number from 0 to 4 allows us to distribute batteries to run n computers. But as soon as we try 5 or more, it’s no longer possible because we don’t have enough battery power to sustain all computers simultaneously.
Let's call the maximum number of minutes all computers can run simultaneously as maxMinutes. Any number of minutes from maxMinutes+1 to sum(batteries) // n won’t work because it will always result in insufficient power.
However, any number of minutes from 0 to maxMinutes will allow us to run all computers.
Therefore, maxMinutes is the largest number of minutes all computers can run while ensuring n computers are powered, and we return maxMinutes as the answer. Any number from 0 to maxMinutes will work because we can still distribute power efficiently, but as soon as we try maxMinutes + 1 or more, it won’t be possible anymore.
Explaining the Battery Distribution Process in Real-World Terms
Imagine you have n computers that need to be powered, and a set of batteries with different energy capacities. Your task is to figure out how long you can keep all n computers running, ensuring that each computer always has a power source. The challenge is to maximize this duration while using the batteries efficiently.
Step 1: Setting Up the Process
To start, you need to determine if it’s possible to run all computers for a given x minutes. Think of x as the minimum number of minutes you want all computers to keep running. If x is too high, you might not have enough battery power to sustain all computers. If x is too low, you might not be maximizing the usage of available battery power.
Step 2: Counting the Total Usable Battery Power
To see if running all n computers for x minutes is possible, you need to count how much total power is available. You do this by going through each battery: For each battery, ask yourself:
How much time can I contribute to sustaining the computers if I need to run each for at least x minutes?
This is calculated as min(batteries[i], x), meaning each battery can contribute at most x minutes of power.
For example, if you have a battery of 10 minutes and you want to sustain all computers for x = 3 minutes, then this battery contributes exactly 3 minutes. By doing this for every battery, you effectively determine the total power available to sustain n computers for x minutes.
Step 3: Keeping Track of Power Distribution
To keep track of whether you can sustain n computers for x minutes, you use a counter called totalPower. Every time you determine how much time a battery contributes (using min(batteries[i], x)), you add that number to totalPower. This is similar to keeping a tally of how much energy you have available as you go through each battery.
Step 4: Checking if the Goal is Met
Once you’ve counted all the available power: You check if totalPower is greater than or equal to n × x.
The condition totalPower ≥ n × x is essential because it verifies whether we have enough total energy to run all n computers for x minutes.
Each computer requires x minutes of power, so collectively, the total power needed is n × x. To calculate the available power, we sum the contributions from all batteries. Each battery can contribute either its full capacity (if it's less than or equal to x) or exactly x minutes (if its capacity is greater than x). This ensures no battery is overused beyond its limit.
By comparing the total available power (totalPower) to the required power (n × x), we can determine if the desired runtime is achievable. If totalPower meets or exceeds n × x, we have sufficient energy to sustain all computers for x minutes.
Conversely, if totalPower falls short, it means there isn’t enough power to meet the requirement. This approach effectively leverages the combined contributions of all batteries, even if no single battery alone can sustain a computer for x minutes.
Why This Works in the Real World
- Summing up the total power from all batteries helps you determine if you can sustain all computers for x minutes.
- Keeping track of totalPower ensures that all computers receive enough power.
- This method guarantees that you are fairly maximizing the runtime while ensuring that all n computers remain operational as long as possible.
Let's understand with an example:
Maximum Running Time of N Computers Example:
Dry Run for n = 2, batteries = [1,1,1,1]
We need to maximize the number of minutes we can power n = 2 computers using the given batteries.
We start from t = 0 (minimum possible time) and go up to t = sum(batteries) / n = 2.
- t = 0
- Total powered computers = 1/0+1/0+1/0+1/0 → Infinite computers (always possible). Valid
- t = 1
- Total powered computers = 1/1+1/1+1/1+1/1
- 1+1+1+1=4.
- Since 4 ≥ 2, valid.
- t = 2
- Total powered computers = 1/2+1/2+1/2+1/2 = 2
- Since 4 ≥ 2, valid.
Since t = 2 was the maximum valid time, the maximum minutes the computers can run is 2.
Output: 2
Steps to Implement the Solution:
- Define the check Function:
- Compute the total available battery time.
- For each battery, add min(battery, time) to the total sum.
- Return true if the total sum is at least time * n.
- Implement maxRunTime Function:
- Calculate the total sum of all battery capacities.
- Set low to 0 and high to sum / n.
- Initialize ans to store the maximum valid runtime.
- Iterate Over Possible Runtimes:
- Loop from low to high (brute force approach).
- Call check(n, batteries, i) to verify if i is a valid runtime.
- If valid, update ans to i.
- Return the Maximum Valid Runtime:
- The last valid value stored in ans is the final result.
Maximum Running Time of N Computers leetcode solution
Maximum Running Time of N Computers solution / Code Implementation
1. Maximum Running Time of N Computers solution in c++ Try on Compiler
// C++ Implementation
class Solution {
// Function to check if we can run 'n' computers for 'time' minutes
bool check(int n, vector<int>& batteries, long time)
{
// Variable to store the total available battery time
long sum = 0;
// Iterate over each battery
for (int i : batteries)
{
// Add the minimum of the battery capacity and 'time' to sum
sum += min((long)i, time);
}
// Return true if total available battery time is at least 'time * n'
return sum >= time * n;
}
public:
// Function to find the maximum runtime for 'n' computers
long long maxRunTime(int n, vector<int>& batteries)
{
// Compute the total sum of all battery capacities
long long sum = accumulate(batteries.begin(), batteries.end(), 0LL);
// Set the lower bound to 0
long long low = 0;
// Set the upper bound to sum / n (maximum possible runtime per computer)
long long high = sum / n;
// Variable to store the final answer
long long ans = 0;
// Iterate over all possible runtimes from 'low' to 'high'
for (int i = low; i <= high; i++)
{
// Check if we can sustain 'i' minutes runtime for 'n' computers
if (check(n, batteries, i)) {
// Update the answer if it's valid
ans = i;
}
}
// Return the maximum valid runtime
return ans;
}
};2. Maximum Running Time of N Computers solution in Java Try on Compiler
// Java Implementation
class Solution {
// Function to check if we can run 'n' computers for 'time' minutes
private boolean check(int n, int[] batteries, long time) {
// Variable to store the total available battery time
long sum = 0;
// Iterate over each battery
for (int i : batteries) {
// Add the minimum of the battery capacity and 'time' to sum
sum += Math.min((long) i, time);
}
// Return true if total available battery time is at least 'time * n'
return sum >= time * n;
}
// Function to find the maximum runtime for 'n' computers
public long maxRunTime(int n, int[] batteries) {
// Compute the total sum of all battery capacities
long sum = 0;
for (int battery : batteries) {
sum += battery;
}
// Set the lower bound to 0
long low = 0;
// Set the upper bound to sum / n (maximum possible runtime per computer)
long high = sum / n;
// Variable to store the final answer
long ans = 0;
// Iterate over all possible runtimes from 'low' to 'high'
for (long i = low; i <= high; i++) {
// Check if we can sustain 'i' minutes runtime for 'n' computers
if (check(n, batteries, i)) {
// Update the answer if it's valid
ans = i;
}
}
// Return the maximum valid runtime
return ans;
}
}3. Maximum Running Time of N Computers solution in Python Try on Compiler
# Python Implementation
class Solution:
# Function to check if we can run 'n' computers for 'time' minutes
def check(self, n, batteries, time):
# Compute the total available battery time
total = sum(min(battery, time) for battery in batteries)
# Return true if total available battery time is at least 'time * n'
return total >= time * n
# Function to find the maximum runtime for 'n' computers
def maxRunTime(self, n, batteries):
# Compute the total sum of all battery capacities
total_sum = sum(batteries)
# Set the lower bound to 0
low = 0
# Set the upper bound to total_sum // n (maximum possible runtime per computer)
high = total_sum // n
# Variable to store the final answer
ans = 0
# Iterate over all possible runtimes from 'low' to 'high'
for i in range(low, high + 1):
# Check if we can sustain 'i' minutes runtime for 'n' computers
if self.check(n, batteries, i):
# Update the answer if it's valid
ans = i
# Return the maximum valid runtime
return ans
4. Maximum Running Time of N Computers solution in Javascript Try on Compiler
/**
* @param {number} n
* @param {number[]} batteries
* @return {number}
*/
// Function to check if we can run 'n' computers for 'time' minutes
var check = function (n, batteries, time) {
// Compute the total available battery time
let sum = batteries.reduce((acc, battery) => acc + Math.min(battery, time), 0);
// Return true if total available battery time is at least 'time * n'
return sum >= time * n;
}
var maxRunTime = function (n, batteries) {
// Compute the total sum of all battery capacities
let sum = batteries.reduce((acc, battery) => acc + battery, 0);
// Set the lower bound to 0
let low = 0;
// Set the upper bound to sum / n (maximum possible runtime per computer)
let high = Math.floor(sum / n);
// Variable to store the final answer
let ans = 0;
// Iterate over all possible runtimes from 'low' to 'high'
for (let i = low; i <= high; i++) {
// Check if we can sustain 'i' minutes runtime for 'n' computers
if (check(n, batteries, i)) {
// Update the answer if it's valid
ans = i;
}
}
// Return the maximum valid runtime
return ans;
};Complexity Analysis of Maximum Running Time of N Computers (brute force):
Time Complexity: O(T*m)
Let's analyze the time complexity of the given approach step by step:
- Computing the total sum of batteries
- This is done using reduce(), which iterates over the batteries array.
- Time Complexity: O(m) (where m is the number of batteries).
- Iterating from low = 0 to high = sum / n
- The number of iterations in the worst case is sum / n.
- Let's denote this value as T.
- Time Complexity: O(T).
- Checking for each i in the loop (check(n, batteries, i))
- Iterates over the batteries array (m elements).
- Time Complexity: O(m) per iteration.
Overall Complexity
Since we are iterating O(T) times and each iteration takes O(m), the final complexity is: O(T*m)
where:
- T = sum / n, which in the worst case can be very large.
- m is the number of batteries.
Space Complexity: O(m)
- Auxiliary Space Complexity: O(1)
The algorithm uses only a few integer variables (sum, low, high, ans) and does not allocate any additional data structures.
Therefore, the auxiliary space complexity is O(1). - Total Space Complexity: O(m)
The only input-dependent space used is the batteries array itself, which contains m elements.
Therefore, the total space complexity is O(m).
Will Brute Force Work Against the Given Constraints?
For the current solution, the time complexity is O(T * m), where m is the number of battery packs (batteries.length) (upper limit: 10⁵) and T is the number of iterations from 0 to sum / n (upper limit: 10⁹ / 10⁵ = 10⁴).
In the worst-case scenario, T could be as large as 10⁴, and m could be 10⁵, leading to a time complexity of O(10⁴ * 10⁵) = O(10⁹).
This time complexity can become inefficient when the sum of all battery capacities is large, particularly when sum / n is close to its upper bound (10⁴) and m is large (10⁵). In such cases, the algorithm may perform up to 10⁹ operations, making it impractical for large inputs.
This solution may not execute efficiently for all test cases, particularly when sum / n is near its upper limit. While it may work for smaller values of sum / n, it could exceed time limits for large inputs where sum / n is close to its maximum constraint.
In competitive programming environments, the typical time complexity limit is around 10⁶ operations per test case. Therefore, for inputs with large values in the batteries array, this time complexity could lead to inefficient execution. To make the solution more optimal and handle all possible cases, optimizations such as binary search could be considered to reduce the time complexity further.
How to optimize it?
In the previous approach, we checked every possible value of the number of minutes each computer can run (from 0 to sum(batteries) // n) and verified if it was possible to run n computers for that many minutes. This gave us O(n * sum(batteries) // n) time complexity, which was too slow and caused TLE (Time Limit Exceeded).
Now, let’s think about improving this.
The main issue was that we checked every possible value of the number of minutes from 0 to sum(batteries) // n, which took a lot of time.
Can we make this part faster?
Yes! Here’s the hint:
We are searching for the maximum number of minutes all n computers can run simultaneously. We know this maximum lies between 0 (minimum possible time) and the sum of all battery capacities divided by n (maximum possible time, assuming batteries are optimally distributed).
Now that we know the two endpoints, 0 and sum(batteries) // n, let's make a few observations:
- The data structure is sorted:
The range of possible minutes is naturally sorted from 0 to sum(batteries) // n. - The search space is monotonic:
- If a certain number of minutes allows us to run n computers, then any smaller number will also work.
- If a certain number does not allow us to run n computers, then any larger number will also fail.
- For example: Suppose the batteries are [3, 3, 3] and n = 2.
- Trying 5 minutes (F) fails to keep 2 computers running.
- Starting from 4 minutes (T), we succeed in running the computers.
- This illustrates the monotonic property: once a number works, it will continue to work for smaller numbers.
- The middle element helps minimize or maximize the search space:
- If we take the middle value of the current range and check if it works (i.e., can we run n computers for that many minutes), we can narrow the search space:If it works, we move to the right half to find a larger valid number of minutes.If it doesn’t work, we move to the left half to find a smaller valid number of minutes.
If we plot a graph with the range of possible minutes on the x-axis and the number of computers we can run on the y-axis, we can observe the following:
- Before the maximum valid number (denoted as maxminutes), we can successfully run n computers. This condition will continue to hold true as we go lower.
- Once we exceed maxminutes, we cannot run n computers for that duration.
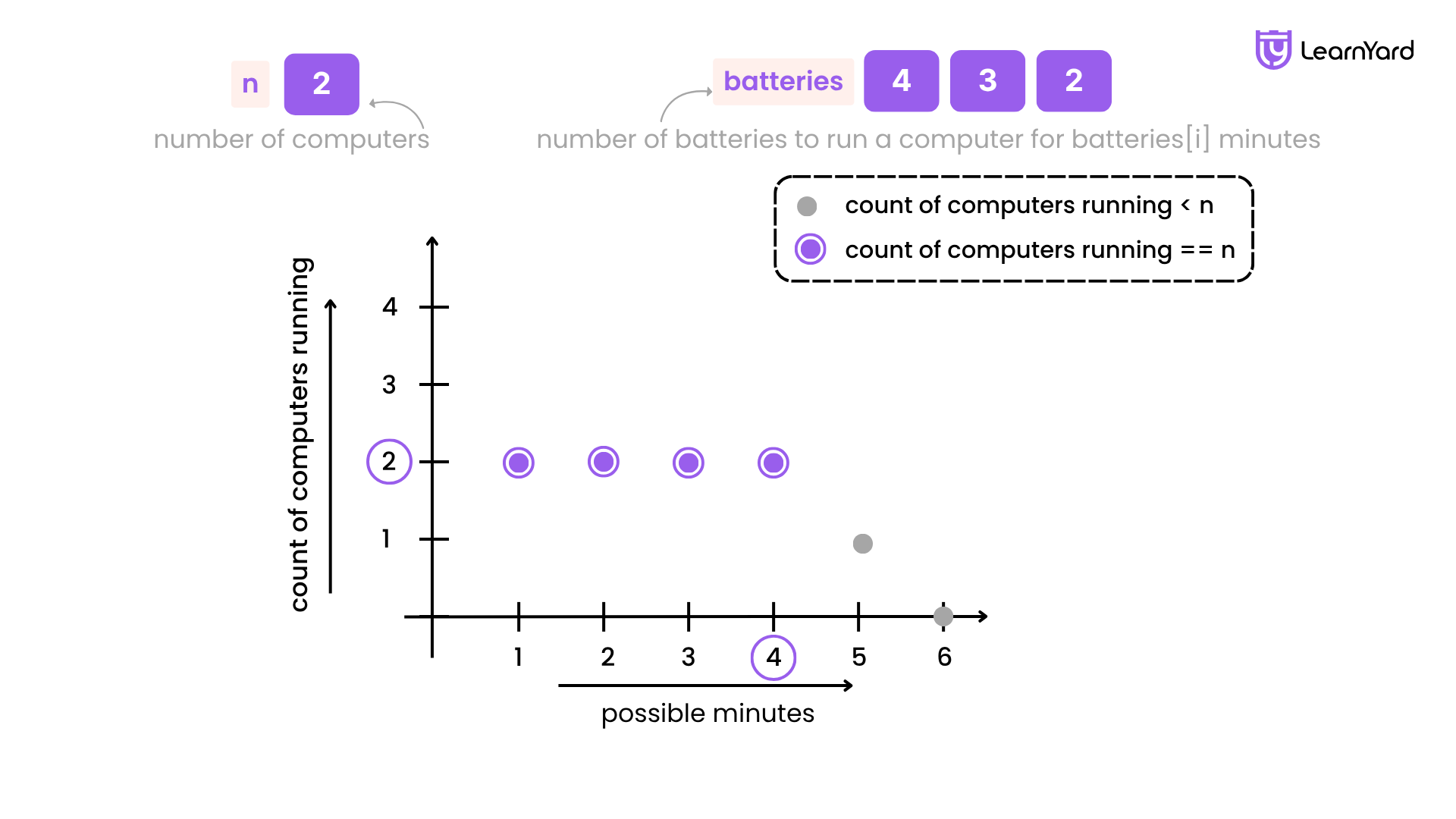
Thus, maxminutes represents the largest number of minutes we can run all n computers simultaneously. Once this number is found, achieving this number of minutes remains feasible for any number less than or equal to maxminutes.
With these points in mind, it's clear that instead of linearly checking all possible values from 0 to sum(batteries) // n, we can take the middle value and continually reduce the search space.
Does this approach remind you of something you've seen before?
Yes, we are applying binary search here. By leveraging the sorted and monotonic properties of the range of possible minutes each computer can run, we efficiently narrow down the search space to find the maximum number that works instead of checking each value linearly.
Maximum Running Time of N Computers Binary Search Approach:
We can simply use binary search to determine the maximum number of minutes all n computers can run simultaneously.
- Start by taking the middle value between low (0) and high (sum(batteries) // n).
- If this mid value satisfies the condition that we can run n computers for at least mid minutes, we store it as a potential answer and narrow the search space to the right half, looking for a larger valid value.
- Otherwise, we move the search to the left half to find a smaller valid value.
- We continue this process as long as low <= high.
- Once the condition breaks, the stored answer is returned as the maximum number of minutes all n computers can run simultaneously.
By using binary search, we can cut the search space in half at each step, which makes the solution much faster and avoids the TLE issue.
This solution follows a greedy approach combined with binary search to efficiently determine the maximum number of minutes the computers can run. By leveraging the sorted nature of the search space, we narrow down the possible runtime values using binary search, ensuring optimal efficiency. The solution also utilizes the array of battery capacities strategically, where each battery's contribution is minimized to either its full capacity or the desired runtime. This ensures that power is distributed in the most efficient way, aligning perfectly with the greedy strategy. The combination of these techniques allows the solution to handle large inputs effectively.
Let us understand this with a video,
Let's understand with an example:
Maximum Running Time of N Computers Example:
Dry Run for Input: n = 2, batteries = [3, 3, 3]
Step 1: Initialize search space
- low = 0, high = (3 + 3 + 3) // 2 = 4
Step 2: Binary Search Iterations
- mid = (0 + 4) // 2 = 2
- Check if 2 minutes is possible:
- Total contribution = 3 + 3 + 3 = 9 (Sufficient for 2 computers × 2 minutes)
- Possible → Update answer = 2 → low = 3
- mid = (3 + 4) // 2 = 3
- Check if 3 minutes is possible:
- Total contribution = 9 (Sufficient for 2 computers × 3 minutes)
- Possible → Update answer = 3 → low = 4
- mid = (4 + 4) // 2 = 4
- Check if 4 minutes is possible:
- Total contribution = 9 (Sufficient for 2 computers × 4 minutes)
- Possible → Update answer = 4 → low = 5
Step 3: Termination
- low > high → Exit loop
Final Answer: 4 minutes
How to code it up:
Step 1: Identify the Problem Requirements
- Understand the problem statement carefully.
- Key requirement: Find the maximum possible runtime for n computers using the given batteries.
Step 2: Binary Search Setup
- Define Search Boundaries:
- Low = 0 (minimum possible runtime).
- High = sum(batteries) / n (maximum possible runtime assuming optimal battery usage).
Step 3: Implement the check() Function
- Purpose: Determine if a given mid value (potential runtime) is achievable.
- Steps:
- Iterate through the batteries array.
- For each battery:
- Add min(battery[i], mid) to a running total (this ensures no battery contributes more than mid).
- Return true if the total accumulated value meets or exceeds mid * n.
Step 4: Binary Search Logic
- While low <= high:
- Compute mid = (low + high) / 2.
- Call the check() function:
- If check(mid) is true, update ans = mid and shift the search space right (low = mid + 1).
- If check(mid) is false, reduce the search space left (high = mid - 1).
Step 5: Return the Final Answer
- The variable ans will hold the maximum achievable runtime.
Maximum Running Time of N Computers leetcode solution
Maximum Running Time of N Computers solution / Code Implementation
1. Maximum Running Time of N Computers solution in c++ Try on Compiler
// C++ Solution with detailed comments
class Solution {
// Function to check if it's possible to run 'n' computers for 'time' minutes
bool check(int n, vector<int>& batteries, long time)
{
// Accumulate the total contribution possible for the given 'time'
long sum = 0;
for(int i : batteries)
{
// Each battery can contribute either its full capacity or 'time' (whichever is smaller)
sum += min((long)i, time);
}
// Return true if total contribution meets or exceeds the required time*n
return sum >= time * n;
}
public:
// Function to calculate the maximum possible runtime for 'n' computers
long long maxRunTime(int n, vector<int>& batteries) {
// Calculate the total battery capacity
long long sum = accumulate(batteries.begin(), batteries.end(), 0LL);
// Set binary search boundaries
long long low = 0;
long long high = sum / n; // Maximum possible runtime in the best case
// Variable to store the result (maximum runtime found)
long long ans = 0;
// Binary search logic
while (low <= high)
{
// Calculate mid-point of the current search space
long long mid = low + (high - low) / 2;
// If 'mid' minutes is achievable, update 'ans' and search for larger value
if (check(n, batteries, mid)) {
ans = mid;
low = mid + 1;
}
// Otherwise, reduce the search space to the left side
else {
high = mid - 1;
}
}
// Return the maximum achievable runtime
return ans;
}
};
2. Maximum Running Time of N Computers solution in Java Try on Compiler
// Java Solution with detailed comments
class Solution {
// Function to check if 'n' computers can run for 'time' minutes
private boolean check(int n, int[] batteries, long time) {
// Accumulate total contribution possible for the given 'time'
long sum = 0;
for(int battery : batteries) {
// Each battery can contribute either its full capacity or 'time'
sum += Math.min((long)battery, time);
}
// Return true if total contribution meets or exceeds the required time*n
return sum >= time * n;
}
// Function to calculate maximum runtime for 'n' computers
public long maxRunTime(int n, int[] batteries) {
// Calculate the total battery capacity
long sum = 0;
for(int battery : batteries) sum += battery;
// Set binary search boundaries
long low = 0, high = sum / n;
// Variable to store the result (maximum runtime found)
long ans = 0;
// Binary search logic
while (low <= high) {
// Calculate mid-point of the current search space
long mid = low + (high - low) / 2;
// If 'mid' minutes is achievable, update 'ans' and search for larger value
if (check(n, batteries, mid)) {
ans = mid;
low = mid + 1;
} else {
high = mid - 1;
}
}
// Return the maximum achievable runtime
return ans;
}
}3. Maximum Running Time of N Computers solution in Python Try on Compiler
# Python Solution with detailed comments
class Solution:
# Function to check if 'n' computers can run for 'time' minutes
def check(self, n, batteries, time):
# Accumulate total contribution possible for the given 'time'
total = sum(min(battery, time) for battery in batteries)
# Return true if total contribution meets or exceeds the required time*n
return total >= time * n
# Function to calculate maximum runtime for 'n' computers
def maxRunTime(self, n, batteries):
# Calculate the total battery capacity
total_sum = sum(batteries)
# Set binary search boundaries
low, high = 0, total_sum // n
# Variable to store the result (maximum runtime found)
ans = 0
# Binary search logic
while low <= high:
# Calculate mid-point of the current search space
mid = (low + high) // 2
# If 'mid' minutes is achievable, update 'ans' and search for larger value
if self.check(n, batteries, mid):
ans = mid
low = mid + 1
else:
high = mid - 1
# Return the maximum achievable runtime
return ans4. Maximum Running Time of N Computers solution in Javascript Try on Compiler
// JavaScript Solution with detailed comments
var maxRunTime = function(n, batteries) {
// Function to check if 'n' computers can run for 'time' minutes
function check(n, batteries, time) {
// Accumulate total contribution possible for the given 'time'
let total = 0;
for (let battery of batteries) {
total += Math.min(battery, time);
}
// Return true if total contribution meets or exceeds the required time*n
return total >= time * n;
}
// Calculate the total battery capacity
let totalSum = batteries.reduce((a, b) => a + b, 0);
// Set binary search boundaries
let low = 0, high = Math.floor(totalSum / n);
// Variable to store the result (maximum runtime found)
let ans = 0;
// Binary search logic
while (low <= high) {
// Calculate mid-point of the current search space
let mid = Math.floor((low + high) / 2);
// If 'mid' minutes is achievable, update 'ans' and search for larger value
if (check(n, batteries, mid)) {
ans = mid;
low = mid + 1;
} else {
high = mid - 1;
}
}
// Return the maximum achievable runtime
return ans;
};
Complexity Analysis of Maximum Running Time of N Computers (Binary Search):
Time Complexity : O(m × log(sum(batteries)/n))
Let's break down the time complexity step by step:
1. Binary Search Complexity
- In the binary search loop, we start with the search space ranging from 0 to sum(batteries) / n.
- The maximum possible number of iterations in the binary search is O(log(sum(batteries) / n)).
- Since sum(batteries) can be as large as 10⁹ × 10⁵ in the worst case, this range can be significant.
- Therefore, the binary search complexity is O(log(sum(batteries) / n)).
2. Checking Function Complexity
- In each iteration of the binary search, the check function iterates through the entire batteries array to calculate the total usable battery time.
- This step takes O(m) where m = batteries.length.
3. Overall Complexity
Combining both parts: O(m×log(sum(batteries)/n))
Space Complexity : O(m)
- Auxiliary Space Complexity: O(1)
The algorithm uses only a few integer variables (sum, low, high, ans) and does not allocate any additional data structures.
Therefore, the auxiliary space complexity is O(1). - Total Space Complexity: O(m)
The only input-dependent space used is the batteries array itself, which contains m elements.
Therefore, the total space complexity is O(m).
Similar Problems
Now that we have successfully tackled this problem, let's try these similar problems: Minimize the Maximum Difference of Pairs, Time to Equality, and Maximum Value of Difference of a Pair of Elements and Their Index.
These problems also involve techniques like greedy strategies, binary search, efficient use of arrays, and sometimes leveraging the sorted nature of data for optimal solutions. Applying these concepts can help efficiently solve a wide range of optimization challenges.
Given an integer array nums of size n, return the minimum number of moves required to make all array elements equal.
In one move, you can increment n - 1 elements of the array by 1.
You have an inventory of different colored balls, and there is a customer that wants orders balls of any color.
The customer weirdly values the colored balls. Each colored ball's value is the number of balls of that color you currently have in your inventory. For example, if you own 6 yellow balls, the customer would pay 6 for the first yellow ball. After the transaction, there are only 5 yellow balls left, so the next yellow ball is then valued at 5 (i.e., the value of the balls decreases as you sell more to the customer).
You are given an integer array, inventory, where inventory[i] represents the number of balls of the ith color that you initially own. You are also given an integer orders, which represents the total number of balls that the customer wants. You can sell the balls in any order.
Return the maximum total value that you can attain after selling orders colored balls. As the answer may be too large, return it modulo 109 + 7
You have n tasks and m workers. Each task has a strength requirement stored in a 0-indexed integer array tasks, with the ith task requiring tasks[i] strength to complete. The strength of each worker is stored in a 0-indexed integer array workers, with the jth worker having workers[j] strength. Each worker can only be assigned to a single task and must have a strength greater than or equal to the task's strength requirement (i.e., workers[j] >= tasks[i]).
Additionally, you have pills magical pills that will increase a worker's strength by strength. You can decide which workers receive the magical pills, however, you may only give each worker at most one magical pill.
Given the 0-indexed integer arrays tasks and workers and the integers pills and strength, return the maximum number of tasks that can be completed.
You are given an array time where time[i] denotes the time taken by the ith bus to complete one trip.
Each bus can make multiple trips successively; that is, the next trip can start immediately after completing the current trip. Also, each bus operates independently; that is, the trips of one bus do not influence the trips of any other bus.
You are also given an integer totalTrips, which denotes the number of trips all buses should make in total. Return the minimum time required for all buses to complete at least totalTrips trips.
You have a water dispenser that can dispense cold, warm, and hot water. Every second, you can either fill up 2 cups with different types of water, or 1 cup of any type of water.
You are given a 0-indexed integer array amount of length 3 where amount[0], amount[1], and amount[2] denote the number of cold, warm, and hot water cups you need to fill respectively. Return the minimum number of seconds needed to fill up all the cups.