Maximum Number of Vowels in a Substring of Given Length Solution In C++/Java/Python/JS
Problem Description
Given a string s and an integer k, return the maximum number of vowel letters in any substring of s with length k.
Vowel letters in English are 'a', 'e', 'i', 'o', and 'u'.
What is a Substring?
A substring is a continuous sequence of characters taken from a string, without changing their order.
For example, if the string is "abcde", then "abc", "bcd", and "de" are all valid substrings.
It must be contiguous, meaning we cannot skip characters (e.g., "ace" is not a substring).

Example
Input: s = "abciiidef", k = 3
Output: 3
Explanation: The substring "iii" contains 3 vowel letters.
Input: s = "aeiou", k = 2
Output: 2
Explanation: Any substring of length 2 contains 2 vowels.
Input: s = "leetcode", k = 3
Output: 2
Explanation: "lee", "eet" and "ode" contain 2 vowels.
Constraints
- 1 <= s.length <= 10^5
- s consists of lowercase English letters.
- 1 <= k <= s.length
The very first question that comes to our mind after reading the problem is: How can we determine the maximum number of vowels present in any substring of length k within the given string s?
A natural and straightforward approach is to examine every possible substring of length k and count how many vowels are present in each of them.
To build a strong foundation, let's first understand this brute-force solution step by step.
This will not only help us grasp the core logic clearly but also prepare us to appreciate and transition toward more optimized approach in the future.
Brute-Force Approach
Intuition
We are given a string and asked to find the substring of length k that contains the maximum number of vowels. The first idea that naturally comes to our mind is to try every possible substring of length k, count how many vowels it contains, and track the maximum one. This is a classic brute-force approach where we leave no possibility unchecked. For this, we can use a nested loop. The outer loop will fix the starting index of the substring, and the inner loop will help us build substrings of the same length as k from that starting point.
Generating Substrings of Length k using Nested Loops
To implement this, we’ll fix the starting index of a substring in the outer loop, just like we do when forming subarrays. This loop runs from i = 0 to i = string.length - k, ensuring we only consider valid substrings of length exactly k.
For each fixed starting index i, we use an inner loop with index j to manually collect characters from the string and check whether each character is a vowel. This inner loop runs from j = i to j < i + k. We initialize a variable count = 0 before entering the inner loop, and for each character, we simply check if it is a vowel and increment the count. After the loop, we compare this count with the maximum vowel count found so far to update our result. This manual technique helps us understand how contiguous substrings are formed and how character-based conditions can be checked step by step, just like we manually formed subarrays element by element.
Let’s take an example to understand this clearly. Suppose the string is "abciiidef" and k = 3. Here's how the substrings are collected:
At i = 0, the inner loop collects characters [a, b, c] → substring = "abc"
At i = 1, the inner loop collects characters [b, c, i] → substring = "bci"
At i = 2, the inner loop collects characters [c, i, i] → substring = "cii"
At i = 3, the inner loop collects characters [i, i, i] → substring = "iii"
At i = 4, the inner loop collects characters [i, i, d] → substring = "iid"
At i = 5, the inner loop collects characters [i, d, e] → substring = "ide"
At i = 6, the inner loop collects characters [d, e, f] → substring = "def"
Each substring is of size k = 3, and we count the vowels in each one and keep track of the maximum count found. This step-by-step construction builds strong clarity for learners who are just getting started with string operations and substring-based pattern problems.
Approach
Step 1: Calculate the Length of the String
We first calculate the length of the string s and store it in an integer variable len.
This will help us determine how many substrings of length k we can extract from the string.
Step 2: Initialize the Variable to Track Maximum Vowels
We create a variable maxVowelCount and initialize it to 0.
This variable will store the maximum number of vowels found in any substring of length k.
Step 3: Traverse All Possible Substrings of Length k
We use a loop starting from i = 0 to i <= len - k.
This ensures we cover all possible substrings of length k in the string s.
For each value of i, we consider the substring from index i to i + k - 1.
Step 4: Count Vowels in the Current Substring
Inside the outer loop, we initialize another variable currentCount to 0.
This will count the number of vowels in the current substring of length k.
We then use an inner loop from j = i to j < i + k, and for each character s[j], we check if it is a vowel.
Step 5: Check if the Character is a Vowel
For each character ch = s[j], we check whether it is one of the vowels: 'a', 'e', 'i', 'o', or 'u'.
If yes, we increment currentCount by 1.
Step 6: Update Maximum Vowel Count if Needed
After counting vowels in the current substring, we compare currentCount with maxVowelCount.
If currentCount is greater, we update maxVowelCount with currentCount.
This way, maxVowelCount always holds the highest number of vowels found so far.
Step 7: Return the Final Result
After all iterations, we return maxVowelCount as the final result.
It represents the maximum number of vowels present in any substring of length k within the string s.

Dry Run
Let's do a detailed dry run of the brute-force approach using nested loops for the input:
s = "abciiidef", k = 3
We want to find the maximum number of vowels in any substring of length 3.
Step 1: Initialize Variables
We calculate len = 9, since the string has 9 characters.
We initialize maxVowelCount = 0.
Step 2: Loop Over s to Check All Substrings of Length k = 3
We want to check every substring of length 3.
The outer loop will go from i = 0 to i = 6 (i.e., len - k = 9 - 3).
For each starting index i, we’ll count how many vowels are in the substring s[i..i+2].
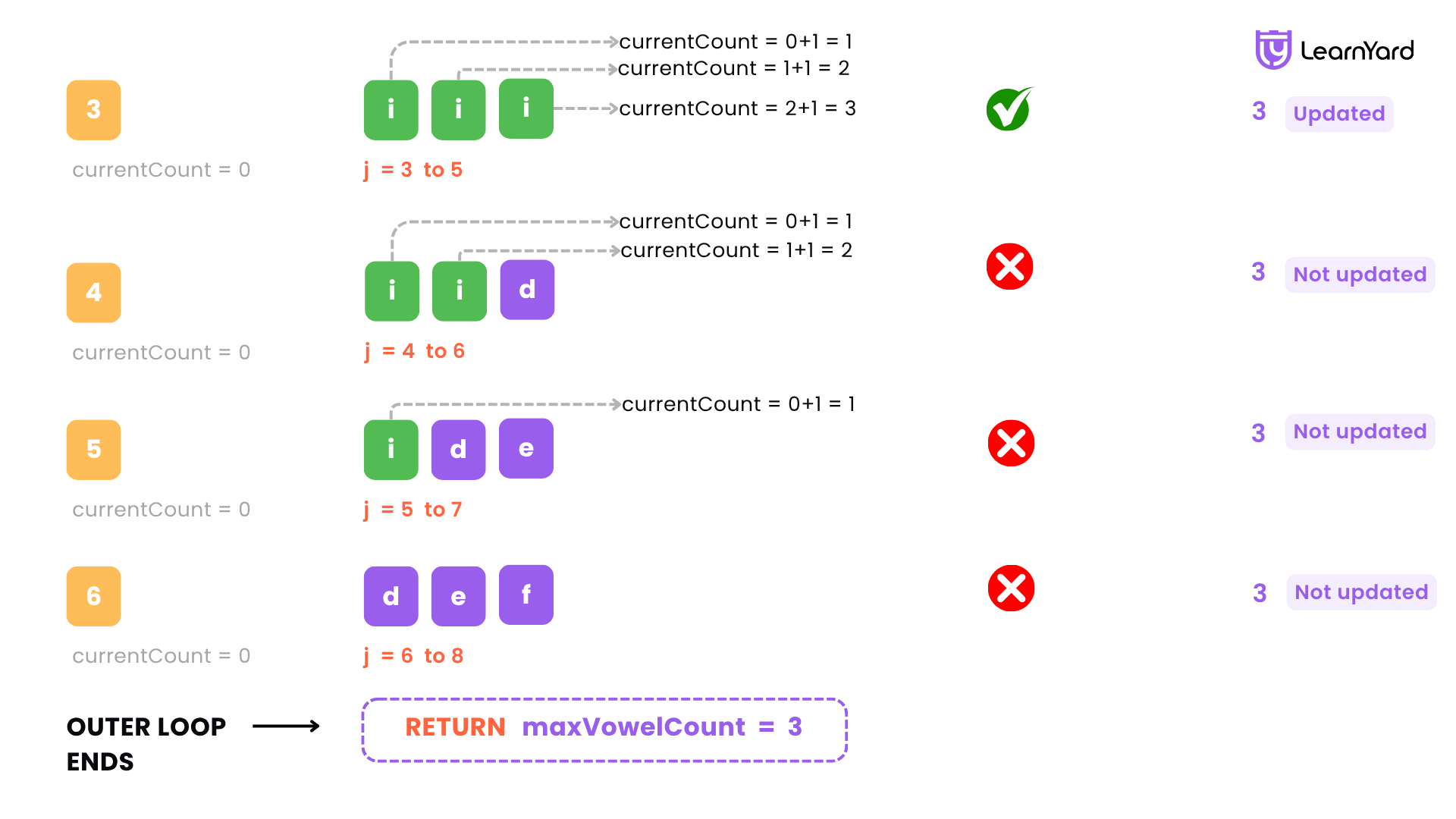
Iteration-Wise Dry Run
i = 0
Substring: s[0..2] = "abc"
Count vowels:
- j = 0 → ch = 'a' → vowel → currentCount = 1
- j = 1 → ch = 'b' → not vowel
- j = 2 → ch = 'c' → not vowel
→ currentCount = 1
maxVowelCount = max(0, 1) → 1
i = 1
Substring: s[1..3] = "bci"
Count vowels:
- j = 1 → ch = 'b' → not vowel
- j = 2 → ch = 'c' → not vowel
- j = 3 → ch = 'i' → vowel → currentCount = 1
→ currentCount = 1
maxVowelCount = max(1, 1) → 1
i = 2
Substring: s[2..4] = "cii"
Count vowels:
- j = 2 → ch = 'c' → not vowel
- j = 3 → ch = 'i' → vowel → currentCount = 1
- j = 4 → ch = 'i' → vowel → currentCount = 2
→ currentCount = 2
maxVowelCount = max(1, 2) → 2
i = 3
Substring: s[3..5] = "iii"
Count vowels:
- j = 3 → ch = 'i' → vowel → currentCount = 1
- j = 4 → ch = 'i' → vowel → currentCount = 2
- j = 5 → ch = 'i' → vowel → currentCount = 3
→ currentCount = 3
maxVowelCount = max(2, 3) → 3
i = 4
Substring: s[4..6] = "iid"
Count vowels:
- j = 4 → ch = 'i' → vowel → currentCount = 1
- j = 5 → ch = 'i' → vowel → currentCount = 2
- j = 6 → ch = 'd' → not vowel
→ currentCount = 2
maxVowelCount = max(3, 2) → 3
i = 5
Substring: s[5..7] = "ide"
Count vowels:
- j = 5 → ch = 'i' → vowel → currentCount = 1
- j = 6 → ch = 'd' → not vowel
- j = 7 → ch = 'e' → vowel → currentCount = 2
→ currentCount = 2
maxVowelCount = max(3, 2) → 3
i = 6
Substring: s[6..8] = "def"
Count vowels:
- j = 6 → ch = 'd' → not vowel
- j = 7 → ch = 'e' → vowel → currentCount = 1
- j = 8 → ch = 'f' → not vowel
→ currentCount = 1
maxVowelCount = max(3, 1) → 3
Final Result
After checking all substrings, the maximum number of vowels found in any substring of length 3 is 3.
This occurs in the substring "iii", which contains three vowels.
Output: 3
Code for All Languages
C++
#include <iostream> // for cin and cout
#include <string> // for using string
using namespace std;
class Solution {
public:
int maxVowels(string s, int k) {
int len = s.length();
int maxVowelCount = 0; // To store the maximum number of vowels found in any substring
// Step 1: Traverse all possible substrings of length k
for (int i = 0; i <= len - k; i++) {
int currentCount = 0; // Count vowels in the current substring
// Step 2: From index i, count vowels in the next k characters
for (int j = i; j < i + k; j++) {
char ch = s[j];
// Step 3: Check if the character is a vowel
if (ch == 'a' || ch == 'e' || ch == 'i' || ch == 'o' || ch == 'u') {
currentCount++;
}
}
// Step 4: Update maxVowelCount if we found a substring with more vowels
if (currentCount > maxVowelCount) {
maxVowelCount = currentCount;
}
}
// Step 5: Return the maximum number of vowels found in any k-length substring
return maxVowelCount;
}
};
// Driver code
int main() {
string s;
int k;
// Input string and integer k
cin >> s >> k;
Solution sol;
int result = sol.maxVowels(s, k);
// Output the maximum number of vowels
cout << result << endl;
return 0;
}Java
import java.util.Scanner; // for taking input
class Solution {
public int maxVowels(String s, int k) {
int len = s.length();
int maxVowelCount = 0; // To store the maximum number of vowels found in any substring
// Step 1: Traverse all possible substrings of length k
for (int i = 0; i <= len - k; i++) {
int currentCount = 0; // Count vowels in the current substring
// Step 2: From index i, count vowels in the next k characters
for (int j = i; j < i + k; j++) {
char ch = s.charAt(j);
// Step 3: Check if the character is a vowel
if (ch == 'a' || ch == 'e' || ch == 'i' || ch == 'o' || ch == 'u') {
currentCount++;
}
}
// Step 4: Update maxVowelCount if we found a substring with more vowels
if (currentCount > maxVowelCount) {
maxVowelCount = currentCount;
}
}
// Step 5: Return the maximum number of vowels found in any k-length substring
return maxVowelCount;
}
}
// Driver code
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
String s = sc.next();
int k = sc.nextInt();
Solution sol = new Solution();
int result = sol.maxVowels(s, k);
// Output the maximum number of vowels
System.out.println(result);
sc.close();
}
}Python
class Solution:
def maxVowels(self, s: str, k: int) -> int:
len_s = len(s)
maxVowelCount = 0 # To store the maximum number of vowels found in any substring
# Step 1: Traverse all possible substrings of length k
for i in range(0, len_s - k + 1):
currentCount = 0 # Count vowels in the current substring
# Step 2: From index i, count vowels in the next k characters
for j in range(i, i + k):
ch = s[j]
# Step 3: Check if the character is a vowel
if ch == 'a' or ch == 'e' or ch == 'i' or ch == 'o' or ch == 'u':
currentCount += 1
# Step 4: Update maxVowelCount if we found a substring with more vowels
if currentCount > maxVowelCount:
maxVowelCount = currentCount
# Step 5: Return the maximum number of vowels found in any k-length substring
return maxVowelCount
# Driver code
if __name__ == "__main__":
s = input()
k = int(input())
sol = Solution()
result = sol.maxVowels(s, k)
# Output the maximum number of vowels
print(result)Javascript
/**
* @param {string} s
* @param {number} k
* @return {number}
*/
var maxVowels = function(s, k) {
let len = s.length;
let maxVowelCount = 0; // To store the maximum number of vowels found in any substring
// Step 1: Traverse all possible substrings of length k
for (let i = 0; i <= len - k; i++) {
let currentCount = 0; // Count vowels in the current substring
// Step 2: From index i, count vowels in the next k characters
for (let j = i; j < i + k; j++) {
let ch = s[j];
// Step 3: Check if the character is a vowel
if (ch === 'a' || ch === 'e' || ch === 'i' || ch === 'o' || ch === 'u') {
currentCount++;
}
}
// Step 4: Update maxVowelCount if we found a substring with more vowels
if (currentCount > maxVowelCount) {
maxVowelCount = currentCount;
}
}
// Step 5: Return the maximum number of vowels found in any k-length substring
return maxVowelCount;
};
// Driver code
const readline = require('readline');
const rl = readline.createInterface({
input: process.stdin,
output: process.stdout
});
let input = [];
rl.on('line', (line) => {
input.push(line.trim());
if (input.length === 2) {
const s = input[0];
const k = parseInt(input[1]);
const result = maxVowels(s, k);
console.log(result);
rl.close();
}
});Time Complexity: O(n * k)
Outer Loop: O(n - k + 1)
The outer loop runs from i = 0 to i = len - k.
Let’s denote:
- n = length of the string s
- k = length of the substring to check
So, the loop executes approximately (n - k + 1) times, which is O(n) in the worst case.
Inner Loop to Count Vowels: O(k)
For each iteration of the outer loop, we run an inner loop from j = i to j < i + k.
In this loop, we access and check each of the k characters of the current substring.
Each character is checked for being a vowel, which is a constant-time operation.
Therefore, this step takes O(k) time per outer iteration.
Vowel Check Operation: O(1)
The condition (ch == 'a' || ch == 'e' || ch == 'i' || ch == 'o' || ch == 'u') is a simple comparison chain.
Checking if a character is a vowel takes constant time, i.e., O(1).
Update Maximum Vowel Count: O(1)
The comparison if (currentCount > maxVowelCount) and the update, if needed, both happen in constant time.
So this step also takes O(1) time per outer loop iteration.
Total Time per Outer Loop Iteration: O(k)
Each iteration of the outer loop involves:
- Counting vowels in a k-length substring → O(k)
- Comparing and updating max → O(1)
Total work per iteration = O(k + 1) = O(k)
Final Time Complexity: O(n * k)
Since the outer loop runs O(n) times and each iteration takes O(k) time,
the total time complexity is O(n * k).
Where:
- n = length of the input string s
- k = length of the substring window
Space Complexity: O(1)
Auxiliary Space Complexity: O(1)
This refers to the extra space used by the algorithm that is independent of the input and output storage.
In our brute-force approach, we use:
- An integer variable maxVowelCount to keep track of the maximum number of vowels found so far
- A temporary variable currentCount in each outer loop iteration to count the vowels in the current substring
- A character variable ch to hold the current character while checking for vowels
All of these are simple primitive data types, and none of them depend on the size of the input.
No additional data structures such as arrays or hash tables are used in this approach.
Therefore, the auxiliary space used by the algorithm is constant, i.e., O(1).
Total Space Complexity: O(n)
This includes the space required for:
- Input space: The input string s of length n occupies O(n) space
- Output space: The function returns an integer value, which takes O(1) space
- Auxiliary space: As analyzed above, this is O(1)
Combining all the space requirements:
Total Space Complexity = O(n) + O(1) + O(1) = O(n)
Why this Approach will give TLE?
The main reason this approach is slow and can time out is because of its high time complexity combined with the input size constraints.
According to the constraints:
1 <= s.length <= 10⁵, which means the input string can be as long as 100,000 characters.
Let’s break down why this becomes a problem:
- The outer loop runs from i = 0 to i <= s.length() - k, which can be up to (n - k + 1) ≈ 100,000 in the worst case.
- Inside each iteration, we:
- Traverse a substring of length k
- Count the number of vowels by checking each character one-by-one → O(k) per iteration
So, if k = 100,000 (maximum possible value), the inner loop does 100,000 operations per outer loop iteration.
Now multiplying by the number of starting positions (≈ n = 100,000) gives:
100,000 * 100,000 = 10,000,000,000 operations
That’s 10 billion operations, which is far too many for a program to run within the time limits of most online judges.
Most competitive programming platforms (like LeetCode, Codeforces, etc.) allow around 1 to 2 seconds per test case, with an average of 10⁷ (10 million) operations per second.
When the number of operations exceeds this range, it results in a Time Limit Exceeded (TLE) error.
We have seen the brute-force solution, which taught us how to check for for vowels by exploring all substrings. However, checking each substring costs us extra O(k), which can be quite expensive. Is it possible to eliminate the nested loops and improve the time complexity? Let’s find out as we move on to the optimal approach.
Optimal Approach
Intuition
Let’s take a moment to understand what this problem is really asking. We’re given an array and a number k, and we’re supposed to find a subarray of length k that has the highest average. A subarray, as we know, is a group of elements that are contiguous — right next to each other in the array.
Now, let’s think about how we’d solve this problem without worrying about efficiency — just the simplest way that comes to mind. That means we’ll look at every possible subarray of size k. For each one, we’ll calculate the sum of the k elements, divide it by k to get the average, and then keep track of the maximum average we’ve seen so far.
To do this, we’d use a nested loop: the outer loop would pick the starting point of the subarray, and the inner loop would go k steps forward to calculate the sum of those k elements. It’s straightforward and works just fine — but as the array gets longer, this method starts to slow down. Why?
Because we’re repeating a lot of work. When we move from one subarray to the next, we’re throwing away the entire previous sum and starting fresh, even though most of the elements are the same. That’s why this brute-force approach takes O(n * k) time — and becomes inefficient for large arrays.
So naturally, we ask: can we avoid this repeated work and speed things up?
That’s where the sliding window technique comes in. But before we go there, understanding this brute-force idea gives us a solid foundation — because every optimization starts with identifying what’s being repeated and finding a smarter way to handle it.
Approach
Step 1: Create a Helper Function to Check for Vowels
We define a function isVowel(char ch) that returns true if the given character is one of the lowercase vowels: 'a', 'e', 'i', 'o', or 'u'.
This makes our code cleaner and avoids repeating the same condition multiple times.
Step 2: Calculate the Length of the Input String
We store the length of the input string s in an integer variable len.
This helps us control the window movement and loop conditions as we slide the window across the string.
Step 3: Initialize Variables for Tracking Vowel Counts
We create two variables:
- maxVowelCount initialized to 0, to track the maximum number of vowels in any k-length window.
- currentCount initialized to 0, to count the vowels in the current sliding window.
Step 4: Count Vowels in the First Window of Size k
We loop through the first k characters (from index 0 to k-1).
For each character, we use the isVowel function to check if it's a vowel.
If it is, we increment currentCount.
After this loop, we set maxVowelCount = currentCount, as this is our starting window.
Step 5: Slide the Window One Character at a Time
We now start a loop from i = k to len - 1 to move the window forward by one character in each iteration.
In each iteration:
- If the new character entering the window (s[i]) is a vowel, we increase currentCount.
- If the character leaving the window (s[i - k]) is a vowel, we decrease currentCount.
Step 6: Update Maximum Vowel Count After Each Slide
After adjusting the currentCount, we check if it's greater than the current maxVowelCount.
If so, we update maxVowelCount with currentCount.
Step 7: Return the Final Answer
Once the loop finishes, maxVowelCount holds the highest number of vowels found in any window of size k.
We return this value as the final result.
Dry Run
Let's do a detailed dry run of the sliding window approach for the input:
s = "abciiidef", k = 3
We want to find the maximum number of vowels in any substring of length 3.
Step 1: Initialize Variables
We calculate len = 9, since the string has 9 characters.
We initialize maxVowelCount = 0 and currentCount = 0.
Step 2: Initialize the First Window of Size k = 3
We count vowels in the first 3 characters:
- i = 0 → 'a' → vowel → currentCount = 1
- i = 1 → 'b' → not vowel → currentCount = 1
- i = 2 → 'c' → not vowel → currentCount = 1
Set maxVowelCount = 1.
Step 3: Slide the Window from Left to Right
Now, we slide the window by one character at a time, from i = 3 to 8.
Iteration-Wise Dry Run
i = 3 (Window: s[1..3] = "bci")
- Add s[3] = 'i' → vowel → currentCount = 2
- Remove s[0] = 'a' → vowel → currentCount = 1
Update maxVowelCount = max(1, 1) = 1
i = 4 (Window: s[2..4] = "cii")
- Add s[4] = 'i' → vowel → currentCount = 2
- Remove s[1] = 'b' → not vowel → currentCount = 2
Update maxVowelCount = max(1, 2) = 2
i = 5 (Window: s[3..5] = "iii")
- Add s[5] = 'i' → vowel → currentCount = 3
- Remove s[2] = 'c' → not vowel → currentCount = 3
Update maxVowelCount = max(2, 3) = 3
i = 6 (Window: s[4..6] = "iid")
- Add s[6] = 'd' → not vowel → currentCount = 3
- Remove s[3] = 'i' → vowel → currentCount = 2
Update maxVowelCount = max(3, 2) = 3
i = 7 (Window: s[5..7] = "ide")
- Add s[7] = 'e' → vowel → currentCount = 3
- Remove s[4] = 'i' → vowel → currentCount = 2
Update maxVowelCount = max(3, 2) = 3
i = 8 (Window: s[6..8] = "def")
- Add s[8] = 'f' → not vowel → currentCount = 2
- Remove s[5] = 'i' → vowel → currentCount = 1
Update maxVowelCount = max(3, 1) = 3
Final Result
After sliding through all windows of size 3, the maximum number of vowels found is 3.
This occurs in the substring "iii" at s[3..5].
Output: 3
Code for All Languages
C++
#include <iostream> // for cin and cout
#include <string> // for using string
using namespace std;
class Solution {
public:
// Helper function to check if a character is a vowel
bool isVowel(char ch) {
return (ch == 'a' || ch == 'e' || ch == 'i' || ch == 'o' || ch == 'u');
}
int maxVowels(string s, int k) {
int len = s.length();
int maxVowelCount = 0; // To store the maximum number of vowels found in any substring
int currentCount = 0; // To count vowels in the current sliding window
// Step 1: Initialize the first window of size k
for (int i = 0; i < k; i++) {
if (isVowel(s[i])) {
currentCount++;
}
}
maxVowelCount = currentCount;
// Step 2: Slide the window from left to right
for (int i = k; i < len; i++) {
if (isVowel(s[i])) {
currentCount++;
}
if (isVowel(s[i - k])) {
currentCount--;
}
// Step 3: Update maxVowelCount if current window has more vowels
if (currentCount > maxVowelCount) {
maxVowelCount = currentCount;
}
}
// Step 4: Return the maximum number of vowels found in any k-length window
return maxVowelCount;
}
};
// Driver code
int main() {
string s;
int k;
// Input string and integer k
cin >> s >> k;
Solution sol;
int result = sol.maxVowels(s, k);
// Output the maximum number of vowels
cout << result << endl;
return 0;
}
Java
import java.util.Scanner; // for taking input
class Solution {
// Helper function to check if a character is a vowel
public boolean isVowel(char ch) {
return (ch == 'a' || ch == 'e' || ch == 'i' || ch == 'o' || ch == 'u');
}
public int maxVowels(String s, int k) {
int len = s.length();
int maxVowelCount = 0; // To store the maximum number of vowels found in any substring
int currentCount = 0; // To count vowels in the current sliding window
// Step 1: Initialize the first window of size k
for (int i = 0; i < k; i++) {
if (isVowel(s.charAt(i))) {
currentCount++;
}
}
maxVowelCount = currentCount;
// Step 2: Slide the window from left to right
for (int i = k; i < len; i++) {
if (isVowel(s.charAt(i))) {
currentCount++;
}
if (isVowel(s.charAt(i - k))) {
currentCount--;
}
// Step 3: Update maxVowelCount if current window has more vowels
if (currentCount > maxVowelCount) {
maxVowelCount = currentCount;
}
}
// Step 4: Return the maximum number of vowels found in any k-length window
return maxVowelCount;
}
}
// Driver class
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
String s = sc.next();
int k = sc.nextInt();
Solution sol = new Solution();
int result = sol.maxVowels(s, k);
// Output the maximum number of vowels
System.out.println(result);
}
}Python
class Solution:
# Helper function to check if a character is a vowel
def isVowel(self, ch):
return ch in ('a', 'e', 'i', 'o', 'u')
def maxVowels(self, s: str, k: int) -> int:
len_s = len(s)
maxVowelCount = 0 # To store the maximum number of vowels found in any substring
currentCount = 0 # To count vowels in the current sliding window
# Step 1: Initialize the first window of size k
for i in range(k):
if self.isVowel(s[i]):
currentCount += 1
maxVowelCount = currentCount
# Step 2: Slide the window from left to right
for i in range(k, len_s):
if self.isVowel(s[i]):
currentCount += 1
if self.isVowel(s[i - k]):
currentCount -= 1
# Step 3: Update maxVowelCount if current window has more vowels
if currentCount > maxVowelCount:
maxVowelCount = currentCount
# Step 4: Return the maximum number of vowels found in any k-length window
return maxVowelCount
# Driver code
if __name__ == "__main__":
s = input()
k = int(input())
sol = Solution()
result = sol.maxVowels(s, k)
# Output the maximum number of vowels
print(result)Javascript
/**
* Helper function to check if a character is a vowel
* @param {char} ch
* @return {boolean}
*/
function isVowel(ch) {
return ch === 'a' || ch === 'e' || ch === 'i' || ch === 'o' || ch === 'u';
}
/**
* @param {string} s
* @param {number} k
* @return {number}
*/
var maxVowels = function(s, k) {
let len = s.length;
let maxVowelCount = 0; // To store the maximum number of vowels found in any substring
let currentCount = 0; // To count vowels in the current sliding window
// Step 1: Initialize the first window of size k
for (let i = 0; i < k; i++) {
if (isVowel(s[i])) {
currentCount++;
}
}
maxVowelCount = currentCount;
// Step 2: Slide the window from left to right
for (let i = k; i < len; i++) {
if (isVowel(s[i])) {
currentCount++;
}
if (isVowel(s[i - k])) {
currentCount--;
}
// Step 3: Update maxVowelCount if current window has more vowels
if (currentCount > maxVowelCount) {
maxVowelCount = currentCount;
}
}
// Step 4: Return the maximum number of vowels found in any k-length window
return maxVowelCount;
};
// Driver code
const readline = require("readline");
const rl = readline.createInterface({
input: process.stdin,
output: process.stdout
});
let inputLines = [];
rl.on("line", function(line) {
inputLines.push(line.trim());
if (inputLines.length === 2) {
let s = inputLines[0];
let k = parseInt(inputLines[1]);
let result = maxVowels(s, k);
console.log(result);
rl.close();
}
});Time Complexity: O(n)
Outer Loop: O(n - k + 1)
The outer loop runs from i = k to i < len, effectively sliding the window across the string from the start to the end minus k.
Let’s denote:
n = length of the string s
k = length of the substring window
So, the loop executes approximately (n - k) times, which is O(n) in the worst case.
Initial Window Setup: O(k)
Before the sliding starts, we initialize the first window of size k by counting vowels in the first k characters.
This involves iterating through k characters and checking if each is a vowel, which takes O(k) time.
Vowel Check Operation: O(1)
The check to determine if a character is a vowel (ch == 'a' || ch == 'e' || ch == 'i' || ch == 'o' || ch == 'u') is a simple constant-time operation.
This occurs every time we add or remove a character from the sliding window.
Sliding Window Updates: O(1) per iteration
For each step when the window slides by one position:
- We add the next character and check if it’s a vowel (constant time)
- We remove the character that is no longer in the window and check if it was a vowel (constant time)
- We update maxVowelCount if needed (constant time)
Total Time per Sliding Step: O(1)
Each slide of the window involves a constant amount of work: two vowel checks and one max update, all O(1).
Final Time Complexity: O(n)
- Initial window setup takes O(k) time
- Sliding over the remaining n - k positions takes O(n - k) ≈ O(n) time with O(1) work per step
Since k ≤ n, the total time complexity simplifies to O(n).
Where:
n = length of the input string s
k = length of the sliding window
Space Complexity: O(1)
Auxiliary Space Complexity: O(1)
This refers to the extra space used by the algorithm that is independent of the input and output storage.
In this sliding window approach, we use:
- An integer variable maxVowelCount to keep track of the maximum number of vowels found so far
- An integer variable currentCount to count the vowels in the current sliding window
- A helper function variable to check if a character is a vowel (which does not use additional space)
All these are simple primitive data types, and none of them depend on the size of the input.
No additional data structures such as arrays, hash tables, or strings are used to store intermediate data.
Therefore, the auxiliary space used by the algorithm is constant, i.e., O(1).
Total Space Complexity: O(n)
This includes the space required for:
- Input space: The input string s of length n occupies O(n) space
- Output space: The function returns an integer value, which takes O(1) space
- Auxiliary space: As analyzed above, this is O(1)
Combining all the space requirements:
Total Space Complexity = O(n) + O(1) + O(1) = O(n)
Learning Tip
Now we have successfully tackled this problem, let's try these similar problems.
Given two strings s and p, return an array of all the start indices of p's anagrams in s. You may return the answer in any order.
Given two strings s1 and s2, return true if s2 contains a permutation of s1, or false otherwise.
In other words, return true if one of s1's permutations is the substring of s2.