Maximum Number of Robots Within Budget Solution In C++/Java/Python/JS
Maximum Number of Robots Within Budget Problem Description:
You have n robots. You are given two 0-indexed integer arrays, chargeTimes and runningCosts, both of length n. The i-th robot costs chargeTimes[i] units to charge and costs runningCosts[i] units to run. You are also given an integer budget.
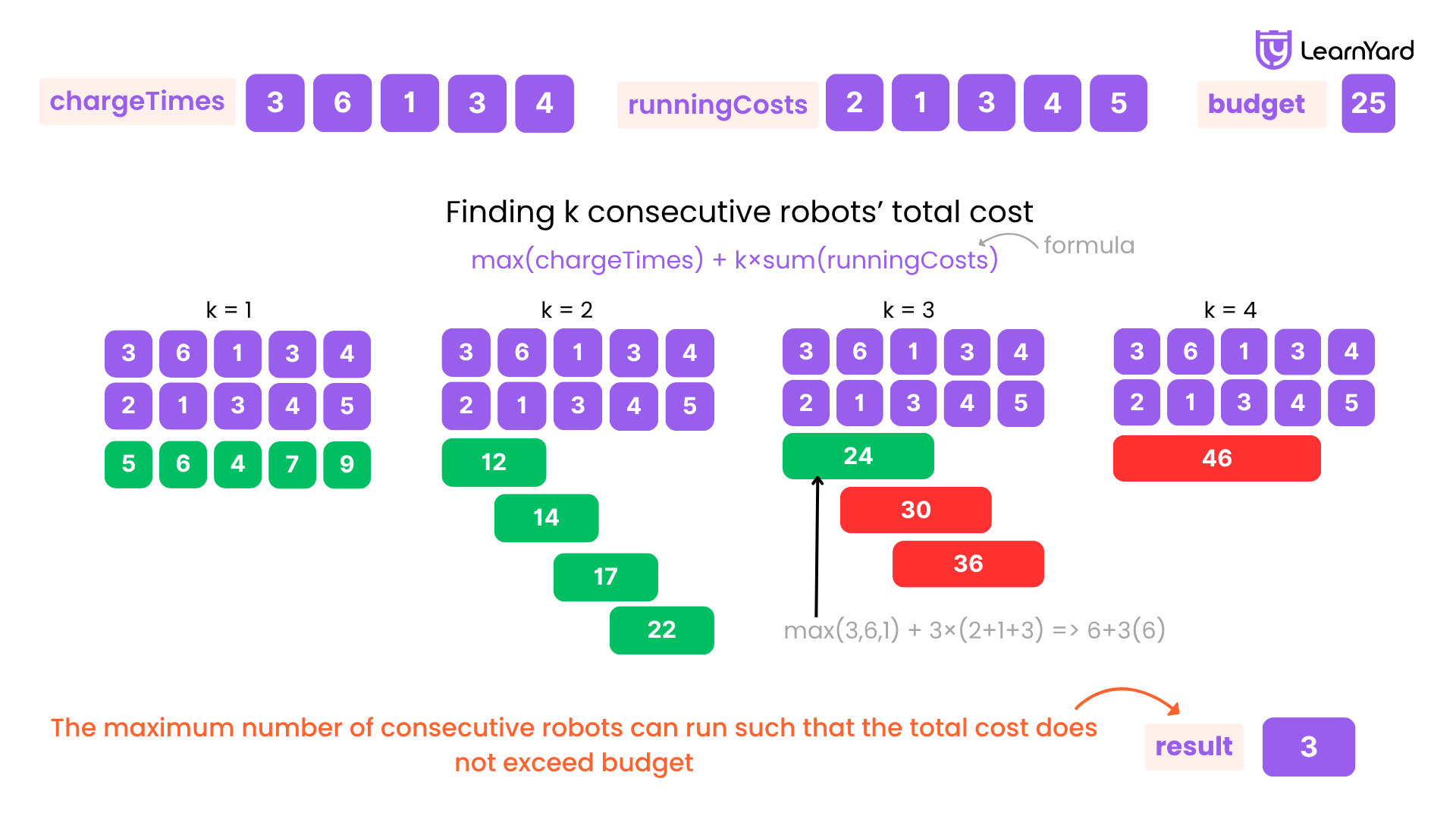
The total cost of running k chosen robots is equal to: max(chargeTimes) + k×sum(runningCosts)
where max(chargeTimes) is the largest charge cost among the k robots and sum(runningCosts) is the sum of running costs among the k robots.
Return the maximum number of consecutive robots you can run such that the total cost does not exceed budget.
Examples:
Input: chargeTimes = [3,6,1,3,4], runningCosts = [2,1,3,4,5], budget = 25
Output: 3
Explanation:
It is possible to run all individual and consecutive pairs of robots within budget.
To obtain answer 3, consider the first 3 robots.
The total cost will be: max(3,6,1) + 3×∑(2,1,3) = 6+3×6 = 24
which is less than 25.
It can be shown that it is not possible to run more than 3 consecutive robots within budget, so we return 3.
Input: chargeTimes = [11,12,19], runningCosts = [10,8,7], budget = 19
Output: 0
Explanation: No robot can be run that does not exceed the budget, so we return 0.
Constraints:
chargeTimes.length == runningCosts.length == n
1 ≤ n ≤ 5 × 10⁴
1 ≤ chargeTimes[i], runningCosts[i] ≤ 10⁵
1 ≤ budget ≤ 10¹⁵
Brute Force Approach
To approach the problem, we are given an integer n representing the number of robots and two integer arrays chargeTimes and runningCosts, where chargeTimes[i] represents the charging cost of the i-th robot and runningCosts[i] represents the running cost per unit time of the i-th robot. We are also given an integer budget that represents the maximum cost we can spend.
Our task is to determine the maximum number of consecutive robots we can run while ensuring that the total cost does not exceed the budget.
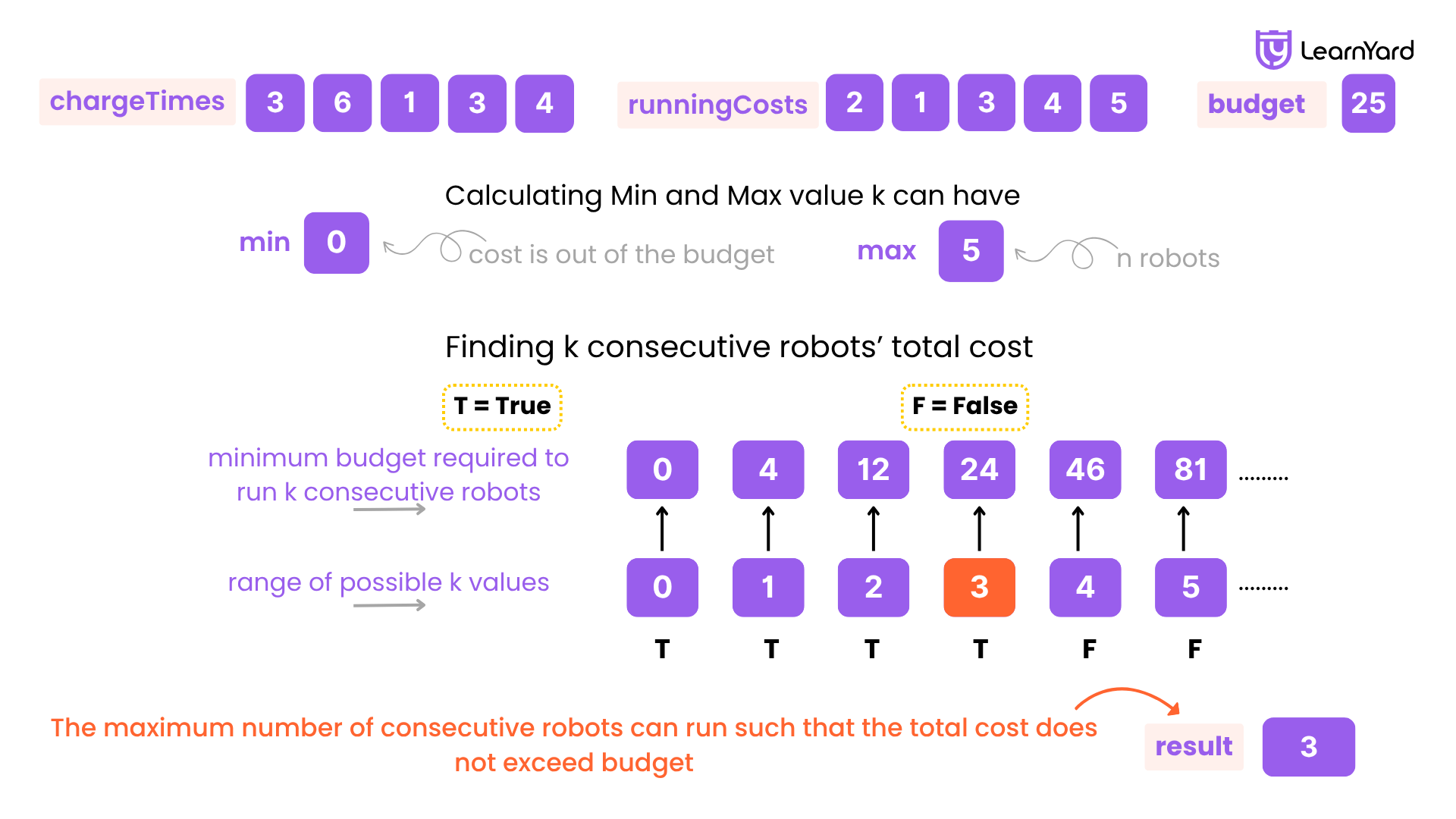
What can be the minimum number of consecutive robots we can run?
The minimum number of consecutive robots required should be 0 because if the smallest possible robot group exceeds the budget, then we cannot run any robots at all, and the answer must be 0.
What would be the maximum number of consecutive robots we can run?
The maximum number of robots we can run should be n because, in the best case, if the budget allows, we can run all robots together. However, if the budget is too small, we may only be able to run fewer robots.
Thus, our search space for the answer ranges from 0 to n. Now, the problem reduces to finding the maximum number of consecutive robots we can run while ensuring the total cost remains within the budget.
A basic approach is to iterate through all possible values from 0 to n and check whether it is possible to keep that many consecutive robots running within the budget.
If it is possible, then it is a valid solution. We continue this process until we find the maximum number of consecutive robots that allow us to stay within the budget. We can either start from 0 to n and stop whenever we find the point where it's not possible, or start from n down to 0 and return the first valid number.
Consider chargeTimes = [3,6,1,3,4], runningCosts = [2,1,3,4,5], and budget = 25.
We start by setting the smallest possible value as 0 and the largest possible value as n = 5.
We then check if it is possible to run all n robots for different values of consecutive robots:
- If we try running 0 robots, it trivially works.
- If we try running 1, 2, or 3 robots, we can manage within the budget, so they are valid.
- If we try running 4 robots, we check:
- Total Cost = max(6,1,3,4) + 4 × sum(2,1,3,4)
- Total Cost = 6 + 4 × 10 = 46, which exceeds the budget.
- This means we cannot run 4 robots.
Since 4 is the first point where it's not possible, we return 3, the last valid number. Thus, the answer is 3.
We can see that any number of robots from 0 to 3 allows us to stay within budget. However, as soon as we try 4 or more, it’s no longer possible because the cost exceeds the budget.
Let's call the maximum number of consecutive robots we can run as maxRobots. Any number of robots from maxRobots + 1 to n won’t work because it will always exceed the budget. However, any number from 0 to maxRobots will be valid.
Therefore, maxRobots is the largest number of consecutive robots we can run while ensuring that we stay within the budget, and we return maxRobots as the answer. Any number from 0 to maxRobots will work, but as soon as we try maxRobots + 1 or more, it won’t be possible anymore.
Explaining the Robot Running Process in Real-World Terms
Imagine you have n robots that need to be run, and each robot has two associated costs:
- Charging Cost → Represents the initial cost to charge the robot.
- Running Cost → Represents the cost incurred per unit time while the robot is running.
Your goal is to determine how many consecutive robots can be run while ensuring that the total cost remains within the given budget. The challenge is to maximize the number of robots while efficiently managing costs.
Step 1: Setting Up the Process
To start, you need to determine if it’s possible to run k consecutive robots within the budget. Think of k as the number of robots you want to keep running at the same time.
- If k is too high, the cost may exceed the budget.
- If k is too low, you might not be maximizing the number of robots you can run.
Thus, we need to check if running k robots is feasible under the given budget.
Step 2: Tracking the Maximum Charge Cost in the k Robots
Each robot has a charging cost, which represents the initial expense required to power it up. When selecting k consecutive robots, the total cost includes the most expensive charge cost among these robots.
To compute the total cost for a given set of k consecutive robots, we use the formula:
Total Cost = max(chargeTimes) + k × sum(runningCosts)
- The term max(chargeTimes) represents the highest charge cost among the selected robots.
- Since max(chargeTimes) directly affects the total cost, it is critical to track this value efficiently.
- If we calculate max(chargeTimes) from scratch for every possible k-sized window, the solution becomes too slow (brute force would require O(n × k) time).
Thus, the challenge is: How do we efficiently find the maximum charge cost for any k-sized window as we slide through the array?
To solve this problem efficiently, we use a deque (double-ended queue), which helps us track the maximum charge cost dynamically as we slide the window.
Why use a deque?
- A deque allows efficient removal and insertion from both ends.
- Instead of recomputing max(chargeTimes) from scratch every time the window moves, the deque helps us maintain the maximum value dynamically.
- The maximum value is always stored at the front of the deque, and we update it efficiently as we slide through the array.
How does the deque maintain max(chargeTimes)?
- Adding a new robot to the window
- We compare the new robot’s chargeTime with elements already in the deque.
- If the new robot has a higher chargeTime than the last element in the deque, we remove the smaller elements.
- This ensures that the deque always maintains values in decreasing order.
- Finally, we add the new robot’s index to the deque.
- Maintaining the maximum charge cost
- The front of the deque always stores the index of the maximum chargeTime for the current window.
- This allows us to retrieve max(chargeTimes) in constant time O(1).
- Sliding the window
- When we move the left boundary of the window forward, we check if the maximum element (stored in the deque’s front) is out of the current window.
- If it is, we remove it from the deque.
Step 3: Calculating the Running Cost in the k Robots
Each robot also has a running cost, which accumulates over time. Since we are running k robots, the total running cost is given by:
Total Running Cost = k × sum(runningCosts)
- We maintain a running sum (runSum) to efficiently calculate this value in a sliding window manner.
- As we add new robots to the window, we update runSum by adding their running cost.
- If the window size exceeds k, we slide it forward by removing the leftmost robot's running cost from runSum.
For example, if runningCosts = [2,1,3,4,5] and we are considering k = 3 robots:
- sum(2,1,3) = 6, so the total running cost is 3 × 6 = 18.
Step 4: Checking the Budget Constraint
Once we have both components (max charge cost and total running cost), we calculate the total cost as:
Total Cost = max(chargeTimes) + k × sum(runningCosts)
- If totalCost ≤ budget, it means running k robots is feasible.
- If totalCost > budget, then we cannot afford to run these k robots.
For example, using:
- maxCharge = 6
- sum(runningCosts) = 6
- Total Cost = 6 + 3 × 6 = 24
If budget = 25, this is valid, so we can run these k = 3 robots.
Why This Works?
To efficiently check different values of k, we use a sliding window approach:
- Expand the window by adding the next robot.
- Maintain the max charge cost using a deque.
- Keep track of the running cost sum dynamically.
- If the window exceeds k, remove the leftmost robot and update the values.
- If the total cost for the current k robots is within the budget, return true.
- If no valid k is found, return false.
Let's understand with an example:
Maximum Number of Robots Within Budget Example:
Input:
- chargeTimes = [3,6,1,3,4]
- runningCosts = [2,1,3,4,5]
- budget = 25
Checking window size k = 1
- (3) → 3 + 1 × (2) = 5 → Valid
- (6) → 6 + 1 × (1) = 7 → Valid
- (1) → 1 + 1 × (3) = 4 → Valid
- (3) → 3 + 1 × (4) = 7 → Valid
- (4) → 4 + 1 × (5) = 9 → Valid
All valid, move to k = 2
Checking window size k = 2
- (3,6) → 6 + 2 × (2+1) = 12 → Valid
- (6,1) → 6 + 2 × (1+3) = 14 → Valid
- (1,3) → 3 + 2 × (3+4) = 17 → Valid
- (3,4) → 4 + 2 × (4+5) = 22 → Valid
All valid, move to k = 3
Checking window size k = 3
- (3,6,1) → 6 + 3 × (2+1+3) = 24 → Valid
- (6,1,3) → 6 + 3 × (1+3+4) = 30 → Not valid
- (1,3,4) → 4 + 3 × (3+4+5) = 34 → Not valid
Valid for one subarray, move to k = 4
Checking window size k = 4
- (3,6,1,3) → 6 + 4 × (2+1+3+4) = 46 → Not valid
- (6,1,3,4) → 6 + 4 × (1+3+4+5) = 58 → Not valid
No valid subarray, break
Final Answer: Maximum k = 3
Steps to Implement the Solution:
Define the Helper Function (isValid)
- Check if it's possible to run k consecutive robots within the budget.
- Use a deque to track the maximum charge time in a sliding window.
- Maintain a running sum of the running costs within the window.
- Adjust the window size dynamically to keep it within k.
- If max(chargeTimes) + k × sum(runningCosts) ≤ budget, return true.
Implement the Main Function (maximumRobots)
- Initialize low = 0 and high = n (total number of robots).
- Iterate over possible values of k, checking validity using isValid().
- Update answer with the largest valid k.
Return the Maximum Number of Robots
- Return the largest k that satisfies the budget condition.
Maximum Number of Robots Within Budget Solution
Maximum Number of Robots Within Budget solution / Code Implementation
1. Maximum Number of Robots Within Budget solution in C++ Try on Compiler
class Solution {
// Function to check if we can run 'k' robots within the given budget
bool isValid(vector<int>& chargeTimes, vector<int>& runningCosts, long long budget, int k)
{
// If k is 0, it's always possible to run 0 robots
if (k == 0)
return true;
// Deque to maintain the maximum chargeTime in the current window
deque<int> maxChargeDeque;
// Variable to store the sum of running costs in the current window
long long runSum = 0;
// Left pointer of the sliding window
int left = 0;
// Iterate through each robot (right pointer of the window)
for (int right = 0; right < chargeTimes.size(); right++) {
// Maintain the deque to store max chargeTimes efficiently
while (!maxChargeDeque.empty() && chargeTimes[maxChargeDeque.back()] <= chargeTimes[right])
{
maxChargeDeque.pop_back();
}
maxChargeDeque.push_back(right);
// Update the running cost sum by adding the current robot's cost
runSum += runningCosts[right];
// If the window size exceeds k, remove the leftmost element
if (right - left + 1 > k)
{
// If the maximum chargeTime is at index 'left', remove it from deque
if (maxChargeDeque.front() == left)
{
maxChargeDeque.pop_front();
}
// Subtract the leftmost running cost and move the left pointer
runSum -= runningCosts[left];
left++;
}
// Check if the total cost is within budget when the window reaches size k
if (right - left + 1 == k) {
long long maxCharge = chargeTimes[maxChargeDeque.front()];
long long totalCost = maxCharge + (long long)k * runSum;
// If the total cost fits within the budget, return true
if (totalCost <= budget) {
return true;
}
}
}
// If no valid subarray of size k is found, return false
return false;
}
public:
// Function to determine the maximum number of robots that can run within budget
int maximumRobots(vector<int>& chargeTimes, vector<int>& runningCosts, long long budget)
{
// Number of robots
int n = chargeTimes.size();
// Initialize search range
int low = 0, high = n, answer = 0;
// Iterate through possible robot counts and check validity
for (int i = low; i <= high; i++)
{
if (isValid(chargeTimes, runningCosts, budget, i)) {
answer = i;
}
}
// Return the maximum number of robots that can be powered within budget
return answer;
}
};
2. Maximum Number of Robots Within Budget solution in Java Try on Compiler
import java.util.*;
class Solution {
// Function to check if we can run 'k' robots within the given budget
private boolean isValid(int[] chargeTimes, int[] runningCosts, long budget, int k) {
// If k is 0, it's always possible to run 0 robots
if (k == 0)
return true;
// Deque to maintain the maximum chargeTime in the current window
Deque<Integer> maxChargeDeque = new ArrayDeque<>();
// Variable to store the sum of running costs in the current window
long runSum = 0;
// Left pointer of the sliding window
int left = 0;
// Iterate through each robot (right pointer of the window)
for (int right = 0; right < chargeTimes.length; right++) {
// Maintain the deque to store max chargeTimes efficiently
while (!maxChargeDeque.isEmpty() && chargeTimes[maxChargeDeque.peekLast()] <= chargeTimes[right]) {
maxChargeDeque.pollLast();
}
maxChargeDeque.addLast(right);
// Update the running cost sum by adding the current robot's cost
runSum += runningCosts[right];
// If the window size exceeds k, remove the leftmost element
if (right - left + 1 > k) {
// If the maximum chargeTime is at index 'left', remove it from deque
if (maxChargeDeque.peekFirst() == left) {
maxChargeDeque.pollFirst();
}
// Subtract the leftmost running cost and move the left pointer
runSum -= runningCosts[left];
left++;
}
// Check if the total cost is within budget when the window reaches size k
if (right - left + 1 == k) {
long maxCharge = chargeTimes[maxChargeDeque.peekFirst()];
long totalCost = maxCharge + (long) k * runSum;
// If the total cost fits within the budget, return true
if (totalCost <= budget) {
return true;
}
}
}
// If no valid subarray of size k is found, return false
return false;
}
// Function to determine the maximum number of robots that can run within budget
public int maximumRobots(int[] chargeTimes, int[] runningCosts, long budget) {
// Number of robots
int n = chargeTimes.length;
// Initialize search range
int low = 0, high = n, answer = 0;
// Iterate through possible robot counts and check validity
for (int i = low; i <= high; i++) {
if (isValid(chargeTimes, runningCosts, budget, i)) {
answer = i;
}
}
// Return the maximum number of robots that can be powered within budget
return answer;
}
}
3. Maximum Number of Robots Within Budget solution in Python Try on Compiler
from collections import deque
class Solution:
# Function to check if we can run 'k' robots within the given budget
def isValid(self, chargeTimes, runningCosts, budget, k):
# If k is 0, it's always possible to run 0 robots
if k == 0:
return True
# Deque to maintain the maximum chargeTime in the current window
maxChargeDeque = deque()
# Variable to store the sum of running costs in the current window
runSum = 0
# Left pointer of the sliding window
left = 0
# Iterate through each robot (right pointer of the window)
for right in range(len(chargeTimes)):
# Maintain the deque to store max chargeTimes efficiently
while maxChargeDeque and chargeTimes[maxChargeDeque[-1]] <= chargeTimes[right]:
maxChargeDeque.pop()
maxChargeDeque.append(right)
# Update the running cost sum by adding the current robot's cost
runSum += runningCosts[right]
# If the window size exceeds k, remove the leftmost element
if right - left + 1 > k:
if maxChargeDeque[0] == left:
maxChargeDeque.popleft()
runSum -= runningCosts[left]
left += 1
# Check if the total cost is within budget when the window reaches size k
if right - left + 1 == k:
maxCharge = chargeTimes[maxChargeDeque[0]]
totalCost = maxCharge + k * runSum
# If the total cost fits within the budget, return True
if totalCost <= budget:
return True
# If no valid subarray of size k is found, return False
return False
# Function to determine the maximum number of robots that can run within budget
def maximumRobots(self, chargeTimes, runningCosts, budget):
n = len(chargeTimes)
low, high, answer = 0, n, 0
for i in range(low, high + 1):
if self.isValid(chargeTimes, runningCosts, budget, i):
answer = i
return answer
4. Maximum Number of Robots Within Budget solution in Javascript Try on Compiler
/**
* Function to check if we can run 'k' robots within the given budget
* @param {number[]} chargeTimes - Array of charge times for each robot
* @param {number[]} runningCosts - Array of running costs for each robot
* @param {number} budget - Available budget
* @param {number} k - Number of consecutive robots to check
* @return {boolean} - Returns true if k robots can run within the budget, otherwise false
*/
function isValid(chargeTimes, runningCosts, budget, k) {
// If k is 0, it's always possible to run 0 robots
if (k === 0) return true;
// Deque to maintain the maximum chargeTime in the current window
let maxChargeDeque = [];
// Variable to store the sum of running costs in the current window
let runSum = 0;
// Left pointer of the sliding window
let left = 0;
// Iterate through each robot (right pointer of the window)
for (let right = 0; right < chargeTimes.length; right++) {
// Maintain the deque to store max chargeTimes efficiently
while (maxChargeDeque.length > 0 && chargeTimes[maxChargeDeque[maxChargeDeque.length - 1]] <= chargeTimes[right]) {
maxChargeDeque.pop();
}
maxChargeDeque.push(right);
// Update the running cost sum by adding the current robot's cost
runSum += runningCosts[right];
// If the window size exceeds k, remove the leftmost element
if (right - left + 1 > k) {
// If the maximum chargeTime is at index 'left', remove it from deque
if (maxChargeDeque[0] === left) {
maxChargeDeque.shift();
}
// Subtract the leftmost running cost and move the left pointer
runSum -= runningCosts[left];
left++;
}
// Check if the total cost is within budget when the window reaches size k
if (right - left + 1 === k) {
let maxCharge = chargeTimes[maxChargeDeque[0]];
let totalCost = maxCharge + k * runSum;
// If the total cost fits within the budget, return true
if (totalCost <= budget) {
return true;
}
}
}
// If no valid subarray of size k is found, return false
return false;
}
/**
* Function to determine the maximum number of robots that can run within budget
* @param {number[]} chargeTimes - Array of charge times for each robot
* @param {number[]} runningCosts - Array of running costs for each robot
* @param {number} budget - Available budget
* @return {number} - Maximum number of robots that can be powered within budget
*/
var maximumRobots = function(chargeTimes, runningCosts, budget) {
// Number of robots
let n = chargeTimes.length;
// Initialize search range
let low = 0, high = n, answer = 0;
// Iterate through possible robot counts and check validity
for (let i = low; i <= high; i++) {
if (isValid(chargeTimes, runningCosts, budget, i)) {
answer = i;
}
}
// Return the maximum number of robots that can be powered within budget
return answer;
};
Maximum Number of Robots Within Budget Complexity Analysis (brute force)
Time Complexity: O(n²)
The code consists of two main functions:
- isValid() - Checks if k robots can be powered within the budget.
- maximumRobots() - Uses a linear search approach to find the maximum valid k.
isValid() Function Complexity
- Maintaining the Deque:
- Each element is added and removed from the deque at most once, leading to O(1) amortized operations per element.
- Across all elements, this results in O(n) total time for deque operations.
- Sliding Window Execution:
- The right pointer iterates O(n) times.
- The left pointer moves at most O(n) times across the entire array.
- This results in O(n) total time for maintaining the window.
Total Complexity of isValid() = O(n)
- maximumRobots() Function Complexity
- The function iterates through all possible values of k from 0 to n.
- For each k, it calls isValid() once.
- This results in O(n) calls to isValid().
Total Complexity of maximumRobots() = O(n) * O(n) = O(n²)
Overall Time Complexity
Since maximumRobots() calls isValid() O(n) times, and each call to isValid() takes O(n) time, the overall worst-case time complexity is:
O(n²) (Quadratic Time Complexity)
This brute-force approach is inefficient for large inputs, and a binary search optimization could reduce the complexity to O(n log n).
Space Complexity: O(n)
- Auxiliary Space Complexity: O(n)
The algorithm uses a deque (maxChargeDeque) to store indices, which at most holds O(n) elements in the worst case.
A few integer and long long variables (runSum, left, right, etc.) use O(1) space.
Therefore, the auxiliary space complexity is O(n). - Total Space Complexity: O(n+m)
The input consists of two arrays: - chargeTimes of size n
- runningCosts of size n
The total space complexity includes input storage, which is O(n + n) = O(n). Additional space is only used for the deque and a few variables, keeping it at O(n) overall.
Final Total Space Complexity = O(n)
Will Brute Force Work Against the Given Constraints?
For the current solution, the time complexity is O(n²), where n is the number of robots.
- The algorithm iterates over all possible window sizes k (from 0 to n).
- For each k, it checks all possible subarrays of size k to verify if they satisfy the budget constraint.
- The validation step for each k runs in O(n) using a sliding window approach with a deque.
Thus, since we perform this check for every possible k, the overall time complexity is O(n²).
In the worst-case scenario, when n is at its maximum constraint (5 × 10⁴), the total number of operations can be as large as (5 × 10⁴)² = 2.5 × 10⁹.
This time complexity can become inefficient when n is large, particularly when n = 5 × 10⁴, leading to nearly 2.5 × 10⁹ operations. While this may be feasible for small inputs, it could lead to inefficient execution and exceed time limits for larger inputs.
In competitive programming, the typical acceptable time complexity limit is around 10⁶ operations per test case. Since this solution may perform significantly more operations (10⁹ in the worst case), it may become impractical for large inputs.
Given these constraints, the O(n²) approach may exceed time limits for large values of n.
How to optimize it?
In the previous approach, we checked every possible value of k (from 0 to n) and verified if it was possible to run k consecutive robots within the budget. This resulted in O(n²) time complexity, which was too slow and caused TLE (Time Limit Exceeded).
Now, let’s think about improving this.
The main issue was that we checked every possible value of k from 0 to n, which took too much time.
Can we make this part faster?
Yes! Here’s the hint:
We are searching for the maximum number of consecutive robots (k) that can run without exceeding the budget. We know this maximum lies between 0 (minimum possible robots) and n (maximum possible robots).
Now that we know the two endpoints, 0 and n, let's make a few observations:
1. The Search Space is Sorted:
The range of possible k is naturally sorted from 0 to n.
2. The Search Space is Monotonic:
- If a certain number of consecutive robots (k) can run within the budget, then any smaller value of k will also work.
- If a certain number k exceeds the budget, then any larger k will also fail.
For example: Suppose the chargeTimes = [3,6,1,3,4], runningCosts = [2,1,3,4,5], and budget = 25.
- Trying k = 4 (F) fails to keep 4 consecutive robots running.
- Trying k = 3 (T) works successfully within the budget.
This illustrates the monotonic property: once a number works, it will continue to work for smaller values.
3. The middle element helps minimize or maximize the search space:
Instead of checking every k linearly, we can use binary search to find the largest valid k efficiently.
- We take the middle value of the current range and check if it works (i.e., can we run k consecutive robots within the budget?).
- If it works, we move to the right half to find a larger valid k.
- If it doesn’t work, we move to the left half to find a smaller valid k.
If we plot a graph with the range of possible k values on the x-axis and the minimum budget required to run k consecutive robots on the y-axis, we can observe the following:
- Before the maximum valid k (denoted as maxK), we can successfully run k robots. This condition will continue to hold for smaller values.
- Once we exceed maxK, we cannot run k robots for that duration.
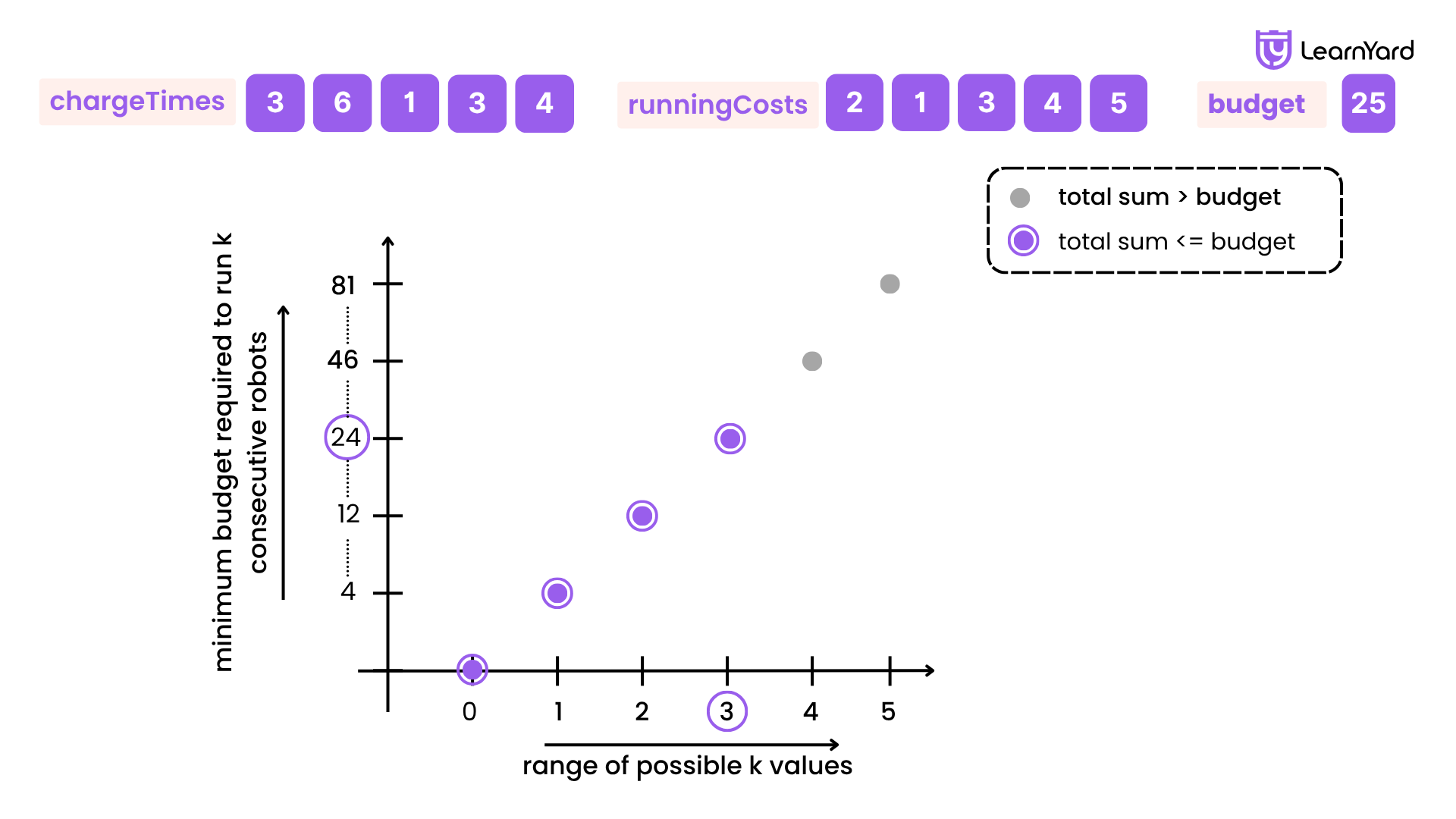
Thus, maxK represents the largest number of consecutive robots we can run within the budget. Once this number is found, achieving this number remains feasible for any k ≤ maxK.
With these points in mind, it's clear that instead of linearly checking all values from 0 to n, we can take the middle value and continually reduce the search space using binary search.
Does this approach remind you of something you've seen before?
Yes! This is a classic binary search optimization for a monotonic search space!
Maximum Consecutive Robots with Binary Search Algorithm:
We can simply use binary search to determine the maximum number of consecutive robots that can run without exceeding the budget.
- Define the search space:
- The possible values of k (number of consecutive robots) range from 0 to n.
- Start with low = 0 and high = n.
- Use binary search:
- Take the middle value mid = (low + high) / 2 as a potential k.
- Check if it is possible to run mid consecutive robots within the budget.
- Adjust the search range based on validity:
- If running mid robots is valid, store it as a potential answer and move to the right half (low = mid + 1) to find a larger valid k.
- If running mid robots exceeds the budget, move to the left half (high = mid - 1) to find a smaller valid k.
- Continue until convergence:
- The process continues as long as low ≤ high.
- Once the condition breaks, the stored answer is returned as the maximum number of consecutive robots that can run within the budget.
Why Binary Search Works?
By using binary search, we cut the search space in half at each step, making the solution much faster and avoiding the TLE issue that occurs with brute force approaches (O(n²)).
This solution follows a greedy approach combined with binary search to efficiently determine the maximum number of consecutive robots that can run.
- The search space is naturally sorted, allowing binary search to be applied.
- The solution optimally distributes the budget, ensuring that resources are used in the most efficient way.
- By checking feasibility in O(n) time per search step, the overall complexity is O(n log n), making it scalable for large inputs.
Let us understand this with a video,
Let's understand with an example:
Maximum Number of Robots Within Budget Example:
Input:
chargeTimes = [3,6,1,3,4]
runningCosts = [2,1,3,4,5]
budget = 25
Step-by-Step Execution:
- Initialize Search Space:
- low = 0, high = 5 (n), answer = 0
- Binary Search Iterations:
- Mid = (0+5)/2 = 2 → Check if k = 2 is valid:
- Possible windows:
- (3,6) → 6 + 2 × (2+1) = 12 Valid
- (6,1) → 6 + 2 × (1+3) = 14 Valid
- (1,3) → 3 + 2 × (3+4) = 17 Valid
- (3,4) → 4 + 2 × (4+5) = 22 Valid
- Valid → Move right → low = 3, answer = 2
- Mid = (3+5)/2 = 4 → Check if k = 4 is valid:
- Possible windows:
- (3,6,1,3) → 6 + 4 × (2+1+3+4) = 46 Not Valid
- (6,1,3,4) → 6 + 4 × (1+3+4+5) = 58 Not Valid
- Not Valid → Move left → high = 3
- Mid = (3+3)/2 = 3 → Check if k = 3 is valid:
- Possible windows:
- (3,6,1) → 6 + 3 × (2+1+3) = 24 Valid
- (6,1,3) → 6 + 3 × (1+3+4) = 30 Not Valid
- Valid → Move right → low = 4, answer = 3
- Exit Binary Search:
- Final Answer = 3
How to code it up:
Define the isValid function
- Maintain a sliding window of k consecutive robots.
- Use a deque to track the maximum chargeTime in the window.
- Keep track of the sum of runningCosts in the window.
- Slide the window if its size exceeds k.
- Check the budget constraint:
- If max(chargeTimes) + k * sum(runningCosts) ≤ budget, return true.
- Otherwise, continue sliding the window.
- Return false if no valid subarray of size k is found.
Implement the maximumRobots function
- Initialize Binary Search:
- low = 0, high = n, answer = 0.
- Perform Binary Search:
- Compute mid = (low + high) / 2.
- If isValid(mid) returns true, update answer = mid and try a larger k (low = mid + 1).
- Otherwise, try a smaller k (high = mid - 1).
- Return the maximum valid k (answer).
Maximum Number of Robots Within Budget Solution
Maximum Number of Robots Within Budget solution / Code Implementation
1. Maximum Number of Robots Within Budget solution in C++ Try on Compiler
class Solution {
// Function to check if it's possible to run 'k' consecutive robots within budget
bool isValid(vector<int>& chargeTimes, vector<int>& runningCosts, long long budget, int k)
{
// If k is 0, it's always valid to run 0 robots
if (k == 0)
return true;
// Deque to store indices of max chargeTimes in the current sliding window
deque<int> maxChargeDeque;
// Variable to maintain the sum of running costs in the current window
long long runSum = 0;
// Left boundary of the sliding window
int left = 0;
// Iterate through the chargeTimes array using right pointer
for (int right = 0; right < chargeTimes.size(); right++) {
// Maintain deque to store max chargeTimes for the current window
while (!maxChargeDeque.empty() && chargeTimes[maxChargeDeque.back()] <= chargeTimes[right])
{
maxChargeDeque.pop_back();
}
// Push current index into the deque
maxChargeDeque.push_back(right);
// Update the sum of running costs in the current window
runSum += runningCosts[right];
// If the window size exceeds 'k', slide the left boundary
if (right - left + 1 > k)
{
// Remove outdated max chargeTime if it is at the left boundary
if (maxChargeDeque.front() == left)
{
maxChargeDeque.pop_front();
}
// Subtract the running cost of the robot at the left boundary
runSum -= runningCosts[left];
// Move the left boundary to the right
left++;
}
// When the window size reaches 'k', check if the budget constraint is met
if (right - left + 1 == k)
{
// Maximum chargeTime in the current window
long long maxCharge = chargeTimes[maxChargeDeque.front()];
// Calculate the total cost for running 'k' robots
long long totalCost = maxCharge + (long long)k * runSum;
// If total cost is within budget, return true
if (totalCost <= budget)
{
return true;
}
}
}
// Return false if no valid subarray of size 'k' is found
return false;
}
public:
// Function to find the maximum number of consecutive robots that can run within budget
int maximumRobots(vector<int>& chargeTimes, vector<int>& runningCosts, long long budget)
{
// Get the number of robots
int n = chargeTimes.size();
// Initialize binary search bounds
int low = 0, high = n, answer = 0;
// Perform binary search on 'k' (length of consecutive robots)
while (low <= high)
{
// Find the middle value
int mid = (low + high) / 2;
// Check if it's valid to run 'mid' consecutive robots within budget
if (isValid(chargeTimes, runningCosts, budget, mid))
{
// Update answer and try for a larger 'k'
answer = mid;
low = mid + 1;
}
else
{
// Try for a smaller 'k'
high = mid - 1;
}
}
// Return the maximum number of robots that can run within budget
return answer;
}
};
2. Maximum Number of Robots Within Budget solution in Java Try on Compiler
import java.util.*;
class Solution {
private boolean isValid(int[] chargeTimes, int[] runningCosts, long budget, int k) {
if (k == 0)
return true;
Deque<Integer> maxChargeDeque = new LinkedList<>();
long runSum = 0;
int left = 0;
for (int right = 0; right < chargeTimes.length; right++) {
while (!maxChargeDeque.isEmpty() && chargeTimes[maxChargeDeque.peekLast()] <= chargeTimes[right]) {
maxChargeDeque.pollLast();
}
maxChargeDeque.addLast(right);
runSum += runningCosts[right];
if (right - left + 1 > k) {
if (maxChargeDeque.peekFirst() == left) {
maxChargeDeque.pollFirst();
}
runSum -= runningCosts[left];
left++;
}
if (right - left + 1 == k) {
long maxCharge = chargeTimes[maxChargeDeque.peekFirst()];
long totalCost = maxCharge + (long) k * runSum;
if (totalCost <= budget) {
return true;
}
}
}
return false;
}
public int maximumRobots(int[] chargeTimes, int[] runningCosts, long budget) {
int n = chargeTimes.length;
int low = 0, high = n, answer = 0;
while (low <= high) {
int mid = (low + high) / 2;
if (isValid(chargeTimes, runningCosts, budget, mid)) {
answer = mid;
low = mid + 1;
} else {
high = mid - 1;
}
}
return answer;
}
}
3. Maximum Number of Robots Within Budget solution in Python Try on Compiler
from collections import deque
class Solution:
def isValid(self, chargeTimes, runningCosts, budget, k):
if k == 0:
return True
maxChargeDeque = deque()
runSum = 0
left = 0
for right in range(len(chargeTimes)):
while maxChargeDeque and chargeTimes[maxChargeDeque[-1]] <= chargeTimes[right]:
maxChargeDeque.pop()
maxChargeDeque.append(right)
runSum += runningCosts[right]
if right - left + 1 > k:
if maxChargeDeque[0] == left:
maxChargeDeque.popleft()
runSum -= runningCosts[left]
left += 1
if right - left + 1 == k:
maxCharge = chargeTimes[maxChargeDeque[0]]
totalCost = maxCharge + k * runSum
if totalCost <= budget:
return True
return False
def maximumRobots(self, chargeTimes, runningCosts, budget):
n = len(chargeTimes)
low, high, answer = 0, n, 0
while low <= high:
mid = (low + high) // 2
if self.isValid(chargeTimes, runningCosts, budget, mid):
answer = mid
low = mid + 1
else:
high = mid - 1
return answer
4. Maximum Number of Robots Within Budget solution in Javascript Try on Compiler
var maximumRobots = function(chargeTimes, runningCosts, budget) {
function isValid(k) {
if (k === 0) return true;
let maxChargeDeque = [];
let runSum = 0;
let left = 0;
for (let right = 0; right < chargeTimes.length; right++) {
while (maxChargeDeque.length > 0 && chargeTimes[maxChargeDeque[maxChargeDeque.length - 1]] <= chargeTimes[right]) {
maxChargeDeque.pop();
}
maxChargeDeque.push(right);
runSum += runningCosts[right];
if (right - left + 1 > k) {
if (maxChargeDeque[0] === left) {
maxChargeDeque.shift();
}
runSum -= runningCosts[left];
left++;
}
if (right - left + 1 === k) {
let maxCharge = chargeTimes[maxChargeDeque[0]];
let totalCost = maxCharge + k * runSum;
if (totalCost <= budget) {
return true;
}
}
}
return false;
}
let low = 0, high = chargeTimes.length, answer = 0;
while (low <= high) {
let mid = Math.floor((low + high) / 2);
if (isValid(mid)) {
answer = mid;
low = mid + 1;
} else {
high = mid - 1;
}
}
return answer;
};
Maximum Number of Robots Within Budget Complexity Analysis (binary search)
Time Complexity: O(n log n)
The solution consists of two main parts:
- Binary Search on k (maximum number of consecutive robots that can run)
- Sliding Window (Deque-based optimization) inside isValid function
Binary Search on k
- We perform binary search on the possible values of k, where k can range from 0 to n.
- The number of iterations of binary search is O(log n).
Sliding Window with Deque (Inside isValid function)
- The isValid function iterates through the chargeTimes array once, making it O(n).
- Inside the loop:
- We maintain a deque (double-ended queue) for the maximum chargeTimes in the window.
- Each element is pushed into and popped out of the deque at most once.
- This makes deque operations O(n) in total across all iterations.
- Other operations inside the loop:
- Computing the running sum takes O(1) per iteration.
- Checking the budget condition takes O(1) per iteration.
- Thus, the isValid function runs in O(n).
Final Complexity Calculation
- The outer binary search runs O(log n) times.
- The inner isValid function runs O(n) each time.
Thus, the total complexity is: O(n log n)
Space Complexity: O(n)
- Auxiliary Space Complexity: O(n)
The only significant extra space used is for the deque that stores indices of chargeTimes, which in the worst case can be O(n).
Therefore, the auxiliary space complexity is O(n). - Total Space Complexity: O(n)
The input arrays chargeTimes and runningCosts each have a size of n, but they are given as input and do not contribute to extra space usage.
The deque takes O(n) in the worst case.
Other variables (such as runSum, left, right, and budget) take O(1) space.
Thus, the total space complexity remains O(n)
Is there any scope for further optimizations?
Imagine you are given a set of robots, and each one has a chargeTime and a runningCost per minute. You have a fixed budget, and your goal is to determine the maximum number of consecutive robots that can operate together without exceeding this budget.
If we choose k consecutive robots, then the total cost of running them is determined by two things:
- The most expensive chargeTime among them → This is a one-time cost.
- The sum of all runningCosts multiplied by k → This is the recurring cost.
Thus, the total cost for a window of k robots is:
- maxChargeTime_in_window + k * sum_of_runningCosts_in_window
- This must be ≤ budget for it to be valid.
The tricky part here is that both maxChargeTime and sum of runningCosts are changing dynamically as we slide through the array. If we were to recalculate maxChargeTime for every possible k, it would make the solution very slow (O(n²) or worse). Instead, we need a way to track the maximum chargeTime efficiently.
We saw in the above approach how we efficiently used a deque to maintain the maximum chargeTime in every valid k-sized window. The deque helped us efficiently track the maximum chargeTime in the window, preventing the need for recalculating it from scratch every time.
But do we really need to check for every k-sized window explicitly? Can we find the maximum number of robots without explicitly enforcing a fixed k-sized window?
Yes! Instead of fixing a window size k and checking if it fits the budget, we can simply slide through the array and dynamically adjust the window size while keeping track of the maximum number of robots that can run together.
How Can We Achieve This?
We will use a sliding window approach to dynamically expand and shrink the window to ensure the robots inside it can run within the budget constraints. This way, we don’t need to explicitly check every k-sized window, but rather greedily try to keep as many robots running together as possible.
Expanding the Window
We start with two pointers: left, which marks the beginning of the window, and right, which expands the window to include more robots. As we expand the window by moving right forward, we add the new robot’s runningCost to the sum and track the maxChargeTime efficiently using a deque.
For example, consider chargeTimes = [3, 6, 1, 3, 4], runningCosts = [2, 1, 3, 4, 5], and budget = 15. We begin with the first robot at right = 0, making the window [3] with a runningCost sum of 2. Moving to right = 1, the window becomes [3, 6] with a runningCost sum of 3. As we expand further to right = 2, the window is [3, 6, 1], and the sum is now 6.
Checking Budget Constraint
For the robots inside the window, we compute the total running cost using the formula:
maxChargeTime + (number of robots * sum of runningCosts). If this value is within the budget, we continue expanding the window. However, if it exceeds the budget, we begin shrinking the window from the left.
Continuing with our example, at right = 3, the window becomes [3, 6, 1, 3], and the sum of runningCosts reaches 10. The maxChargeTime is 6, making the totalCost = 6 + (4 * 10) = 46, which exceeds the budget. Since the total cost is too high, we must shrink the window by removing the leftmost robot.
Shrinking the Window If Needed
If the total cost exceeds the budget, we shrink the window by moving left forward. While doing this, we also remove the chargeTime from the deque if it corresponds to the leftmost position and subtract the runningCost[left] from the total sum.
Going back to our example, the window [3, 6, 1, 3] exceeds the budget, so we remove chargeTime[0] = 3 and runningCost[0] = 2. This updates our window to [6, 1, 3], and we recalculate the totalCost, which now fits within the budget.
Tracking the Maximum Number of Robots
At every step, we update max_k, which stores the largest valid window size seen so far. In our example, at right = 2, the window [3, 6, 1] is valid, so max_k = 3. When we reach right = 3, we exceed the budget and shrink, but the new window [6, 1, 3] is still valid, keeping max_k = 3. At right = 4, the window [6, 1, 3, 4] is valid, so we update max_k = 4.
Instead of checking every k-sized window, we dynamically expand and shrink the window while always trying to keep the maximum number of robots running. This approach avoids unnecessary recalculations and efficiently finds the answer in O(n) time complexity. By maintaining a monotonic deque for maxChargeTime and using a sliding window, we efficiently determine the largest group of robots that can operate within the given budget.
Let us understand this with a video,
Let's understand with an example:
Maximum Number of Robots Within Budget Example:
Input:
chargeTimes = [3,6,1,3,4]
runningCosts = [2,1,3,4,5]
budget = 25
Step-by-Step Execution:
- Initialize: left = 0, max_k = 0, runSum = 0, maxChargeDeque = {}
Expanding the Window (Right Pointer Moves)
- right = 0, window = [3], runSum = 2, maxCharge = 3
- TotalCost = 3 + (1 * 2) = 5 (valid)
- max_k = 1
- right = 1, window = [3,6], runSum = 3, maxCharge = 6
- TotalCost = 6 + (2 * 3) = 12 (valid)
- max_k = 2
- right = 2, window = [3,6,1], runSum = 6, maxCharge = 6
- TotalCost = 6 + (3 * 6) = 24 (valid)
- max_k = 3
- right = 3, window = [3,6,1,3], runSum = 10, maxCharge = 6
- TotalCost = 6 + (4 * 10) = 46 (invalid )
- Shrink from left → left = 1, runSum = 8, window = [6,1,3]
- TotalCost = 6 + (3 * 8) = 30 (invalid )
- Shrink from left → left = 2, runSum = 7, window = [1,3]
- TotalCost = 3 + (2 * 7) = 17 (valid )
- right = 4, window = [1,3,4], runSum = 12, maxCharge = 4
- TotalCost = 4 + (3 * 12) = 40 (invalid )
- Shrink from left → left = 3, runSum = 9, window = [3,4]
- TotalCost = 4 + (2 * 9) = 22 (valid )
Final Answer:
max_k = 3 (largest valid window)
Steps to Implement the Solution:
- Initialize Variables:
- n = chargeTimes.size()
- maxChargeDeque (monotonic deque for tracking max charge times in the window)
- runSum = 0 (sum of running costs in the current window)
- left = 0 (left boundary of the sliding window)
- max_k = 0 (stores the maximum valid robots count)
- Expand the Window (Iterate right from 0 to n-1):
- Maintain the deque for max charge time:
- Remove elements from the back if they are smaller than chargeTimes[right].
- Push right into the deque.
- Update runSum by adding runningCosts[right].
- Check and Adjust the Window (Shrink left if needed):
- Compute totalCost = maxCharge + k * runSum.
- If totalCost > budget:
- Remove left element if it was the maximum charge in the deque.
- Subtract runningCosts[left] from runSum.
- Move left forward.
- Update the Maximum Valid Window Size (max_k).
- Return max_k as the final answer.
Maximum Number of Robots Within Budget Solution
Maximum Number of Robots Within Budget solution / Code Implementation
1. Maximum Number of Robots Within Budget solution in c++ Try on Compiler
class Solution {
public:
int maximumRobots(vector<int>& chargeTimes, vector<int>& runningCosts, long long budget) {
// Get the number of robots available
int n = chargeTimes.size();
// Monotonic deque to track the maximum charge time in the window
deque<int> maxChargeDeque;
// Variable to store the sum of running costs in the current window
long long runSum = 0;
// Left pointer for the sliding window
int left = 0;
// Variable to store the maximum valid number of robots that can be activated
int max_k = 0;
// Iterate over each robot using the right pointer
for (int right = 0; right < n; right++) {
// Maintain the monotonic deque to track the maximum charge time in the window
while (!maxChargeDeque.empty() && chargeTimes[maxChargeDeque.back()] <= chargeTimes[right]) {
maxChargeDeque.pop_back();
}
maxChargeDeque.push_back(right);
// Add the running cost of the new robot to the running sum
runSum += runningCosts[right];
// Shrink the window from the left if the total cost exceeds the budget
while (!maxChargeDeque.empty()) {
// Get the maximum charge time from the deque
long long maxCharge = chargeTimes[maxChargeDeque.front()];
// Calculate the total cost for the current window
long long totalCost = maxCharge + (long long)(right - left + 1) * runSum;
// If the total cost exceeds the budget, shrink the window
if (totalCost > budget) {
// If the leftmost element in the deque is at the left pointer, remove it
if (maxChargeDeque.front() == left) {
maxChargeDeque.pop_front();
}
// Subtract the leftmost running cost from the running sum
runSum -= runningCosts[left];
// Move the left pointer to reduce window size
left++;
} else {
// If the window is valid, stop shrinking
break;
}
}
// Update the maximum valid window size found so far
max_k = max(max_k, right - left + 1);
}
// Return the maximum number of robots that can be activated
return max_k;
}
};2. Maximum Number of Robots Within Budget solution in Java Try on Compiler
import java.util.*;
class Solution {
public int maximumRobots(int[] chargeTimes, int[] runningCosts, long budget) {
// Get the size of the chargeTimes array
int n = chargeTimes.length;
// Monotonic deque to store indices of max chargeTime values in the window
Deque<Integer> maxChargeDeque = new LinkedList<>();
// Variable to store the sum of running costs in the current window
long runSum = 0;
// Left pointer for sliding window
int left = 0;
// Variable to store the maximum valid window size
int max_k = 0;
// Iterate through the array using the right pointer
for (int right = 0; right < n; right++) {
// Maintain the deque to keep track of the max chargeTime in the current window
while (!maxChargeDeque.isEmpty() && chargeTimes[maxChargeDeque.peekLast()] <= chargeTimes[right]) {
maxChargeDeque.pollLast();
}
maxChargeDeque.addLast(right);
// Update the sum of running costs
runSum += runningCosts[right];
// Check if the current window is valid, if not, shrink it
while (!maxChargeDeque.isEmpty()) {
// Get the maximum chargeTime in the window
long maxCharge = chargeTimes[maxChargeDeque.peekFirst()];
// Calculate the total cost of the current window
long totalCost = maxCharge + (long) (right - left + 1) * runSum;
// If totalCost exceeds budget, shrink the window from the left
if (totalCost > budget) {
// Remove outdated max chargeTime if it is at the left pointer
if (maxChargeDeque.peekFirst() == left) {
maxChargeDeque.pollFirst();
}
// Remove leftmost runningCost from sum
runSum -= runningCosts[left];
// Move the left pointer to shrink the window
left++;
}
else {
break; // If within budget, stop shrinking
}
}
// Update the maximum valid window size
max_k = Math.max(max_k, right - left + 1);
}
// Return the maximum number of robots that can be run
return max_k;
}
}
3. Maximum Number of Robots Within Budget solution in Python Try on Compiler
from collections import deque
class Solution:
def maximumRobots(self, chargeTimes, runningCosts, budget):
# Get the size of the chargeTimes array
n = len(chargeTimes)
# Monotonic deque to store indices of max chargeTime values in the window
maxChargeDeque = deque()
# Variable to store the sum of running costs in the current window
runSum = 0
# Left pointer for sliding window
left = 0
# Variable to store the maximum valid window size
max_k = 0
# Iterate through the array using the right pointer
for right in range(n):
# Maintain the deque to keep track of the max chargeTime in the current window
while maxChargeDeque and chargeTimes[maxChargeDeque[-1]] <= chargeTimes[right]:
maxChargeDeque.pop()
maxChargeDeque.append(right)
# Update the sum of running costs
runSum += runningCosts[right]
# Check if the current window is valid, if not, shrink it
while maxChargeDeque:
# Get the maximum chargeTime in the window
maxCharge = chargeTimes[maxChargeDeque[0]]
# Calculate the total cost of the current window
totalCost = maxCharge + (right - left + 1) * runSum
# If totalCost exceeds budget, shrink the window from the left
if totalCost > budget:
# Remove outdated max chargeTime if it is at the left pointer
if maxChargeDeque[0] == left:
maxChargeDeque.popleft()
# Remove leftmost runningCost from sum
runSum -= runningCosts[left]
# Move the left pointer to shrink the window
left += 1
else:
break # If within budget, stop shrinking
# Update the maximum valid window size
max_k = max(max_k, right - left + 1)
# Return the maximum number of robots that can be run
return max_k
4. Maximum Number of Robots Within Budget solution in Javascript Try on Compiler
var maximumRobots = function(chargeTimes, runningCosts, budget) {
// Get the size of the chargeTimes array
let n = chargeTimes.length;
// Monotonic deque to store indices of max chargeTime values in the window
let maxChargeDeque = [];
// Variable to store the sum of running costs in the current window
let runSum = 0;
// Left pointer for sliding window
let left = 0;
// Variable to store the maximum valid window size
let max_k = 0;
// Iterate through the array using the right pointer
for (let right = 0; right < n; right++) {
// Maintain the deque to keep track of the max chargeTime in the current window
while (maxChargeDeque.length && chargeTimes[maxChargeDeque[maxChargeDeque.length - 1]] <= chargeTimes[right]) {
maxChargeDeque.pop();
}
maxChargeDeque.push(right);
// Update the sum of running costs
runSum += runningCosts[right];
// Check if the current window is valid, if not, shrink it
while (maxChargeDeque.length) {
let maxCharge = chargeTimes[maxChargeDeque[0]];
let totalCost = maxCharge + (right - left + 1) * runSum;
if (totalCost > budget) {
if (maxChargeDeque[0] === left) maxChargeDeque.shift();
runSum -= runningCosts[left];
left++;
} else {
break;
}
}
// Update the maximum valid window size
max_k = Math.max(max_k, right - left + 1);
}
// Return the maximum number of robots that can be run
return max_k;
};
Maximum Number of Robots Within Budget Complexity Analysis (two pointers)
Time Complexity: O(n)
The solution efficiently finds the maximum number of robots that can operate within a given budget using a sliding window and a monotonic deque. Let's break down the time complexity step by step.
1. Outer Loop (Right Pointer)
The for loop iterates through the chargeTimes array once, meaning the right pointer moves from 0 to n-1.
Number of iterations: O(n)
2. Maintaining the Monotonic Deque
The monotonic deque stores indices of elements in chargeTimes in decreasing order, ensuring that the maximum element in the window can be accessed in O(1) time.
- Insertion into the deque:
- Each element is added at most once.
- If an element smaller than the current one is at the back, we remove it before adding the new element.
- Each element is pushed and popped at most once, making this operation O(n) in total.
- Removing from the front of the deque:
- The left pointer moves forward when shrinking the window.
- Each element is removed at most once when it exits the window.
- This results in O(n) total pops from the front of the deque.
Overall time complexity for deque operations: O(n)
3. Inner While Loop (Shrinking the Window)
The inner while loop is responsible for shrinking the window when the budget constraint is exceeded.
- The left pointer only moves forward.
- Since each element is processed at most once in the entire array, the total number of left pointer movements is at most n.
- Thus, this loop also runs in O(n) total.
Final Complexity Calculation
- Outer loop (right pointer): O(n)
- Deque operations (inserting and removing elements): O(n)
- Inner while loop (shrinking window using left pointer): O(n)
Since each part is O(n), the overall complexity is:
Final Time Complexity: O(n)
Space Complexity: O(n)
- Auxiliary Space Complexity: O(n)
The most significant extra space used is the monotonic deque, which stores indices of chargeTimes. In the worst case, all n elements are stored in the deque (when elements are in strictly decreasing order).
Additionally, we use a few integer variables (left, max_k) and a long long variable (runSum), which take O(1) constant space.
Therefore, the auxiliary space complexity is O(n) due to the deque storage. - Total Space Complexity: O(n)
The input arrays chargeTimes and runningCosts are given as input and do not count towards extra space.
Apart from the deque, no additional data structures (like hash maps or auxiliary arrays) are used.
Thus, the total space complexity remains O(n).
Similar Problems
To efficiently solve this problem, we use several fundamental data structures and techniques. Since we are dealing with a sequence of robots and their associated charge times and running costs, an array naturally stores these values for easy access. The challenge is to determine the maximum number of consecutive robots that can operate within a given budget, which hints at using the sliding window technique to maintain a valid subarray dynamically. Within this window, we must frequently determine the maximum charge time, making a monotonic queue (implemented using a deque) an optimal choice to fetch the maximum value in constant time. The sum of running costs within the window must be efficiently maintained, and a prefix sum could help in scenarios where we need cumulative sums quickly. Since we are testing different window sizes, we can optimize our approach by applying binary search to determine the largest possible window size that satisfies the budget condition. A heap (priority queue) could also be considered to track the maximum charge time, but the monotonic queue serves the same purpose more efficiently. By carefully combining these techniques, we ensure that the solution remains optimized in terms of both time and space complexity.
Now we have successfully tackled this problem, let's try these similar problems.
You are given an array of integers nums, there is a sliding window of size k which is moving from the very left of the array to the very right. You can only see the k numbers in the window. Each time the sliding window moves right by one position.
Return the max sliding window.
Given two sorted 0-indexed integer arrays nums1 and nums2 as well as an integer k, return the kth (1-based) smallest product of nums1[i] * nums2[j] where 0 <= i < nums1.length and 0 <= j < nums2.length.
You have n tasks and m workers. Each task has a strength requirement stored in a 0-indexed integer array tasks, with the ith task requiring tasks[i] strength to complete. The strength of each worker is stored in a 0-indexed integer array workers, with the jth worker having workers[j] strength. Each worker can only be assigned to a single task and must have a strength greater than or equal to the task's strength requirement (i.e., workers[j] >= tasks[i]).
Additionally, you have pills magical pills that will increase a worker's strength by strength. You can decide which workers receive the magical pills, however, you may only give each worker at most one magical pill.
Given the 0-indexed integer arrays tasks and workers and the integers pills and strength, return the maximum number of tasks that can be completed.
You are given an integer n indicating there are n specialty retail stores. There are m product types of varying amounts, which are given as a 0-indexed integer array quantities, where quantities[i] represents the number of products of the ith product type.
You need to distribute all products to the retail stores following these rules:
A store can only be given at most one product type but can be given any amount of it.
After distribution, each store will have been given some number of products (possibly 0). Let x represent the maximum number of products given to any store. You want x to be as small as possible, i.e., you want to minimize the maximum number of products that are given to any store.
Return the minimum possible x.
You are given an array time where time[i] denotes the time taken by the ith bus to complete one trip.
Each bus can make multiple trips successively; that is, the next trip can start immediately after completing the current trip. Also, each bus operates independently; that is, the trips of one bus do not influence the trips of any other bus.
You are also given an integer totalTrips, which denotes the number of trips all buses should make in total. Return the minimum time required for all buses to complete at least totalTrips trips.