Maximum Erasure Value Solution In C++/Java/Python/JS
Problem Description
You are given an array of positive integers nums and want to erase a subarray containing unique elements. The score you get by erasing the subarray is equal to the sum of its elements.
Return the maximum score you can get by erasing exactly one subarray.
An array b is called to be a subarray of a if it forms a contiguous subsequence of a, that is, if it is equal to a[l],a[l+1],...,a[r] for some (l , r).
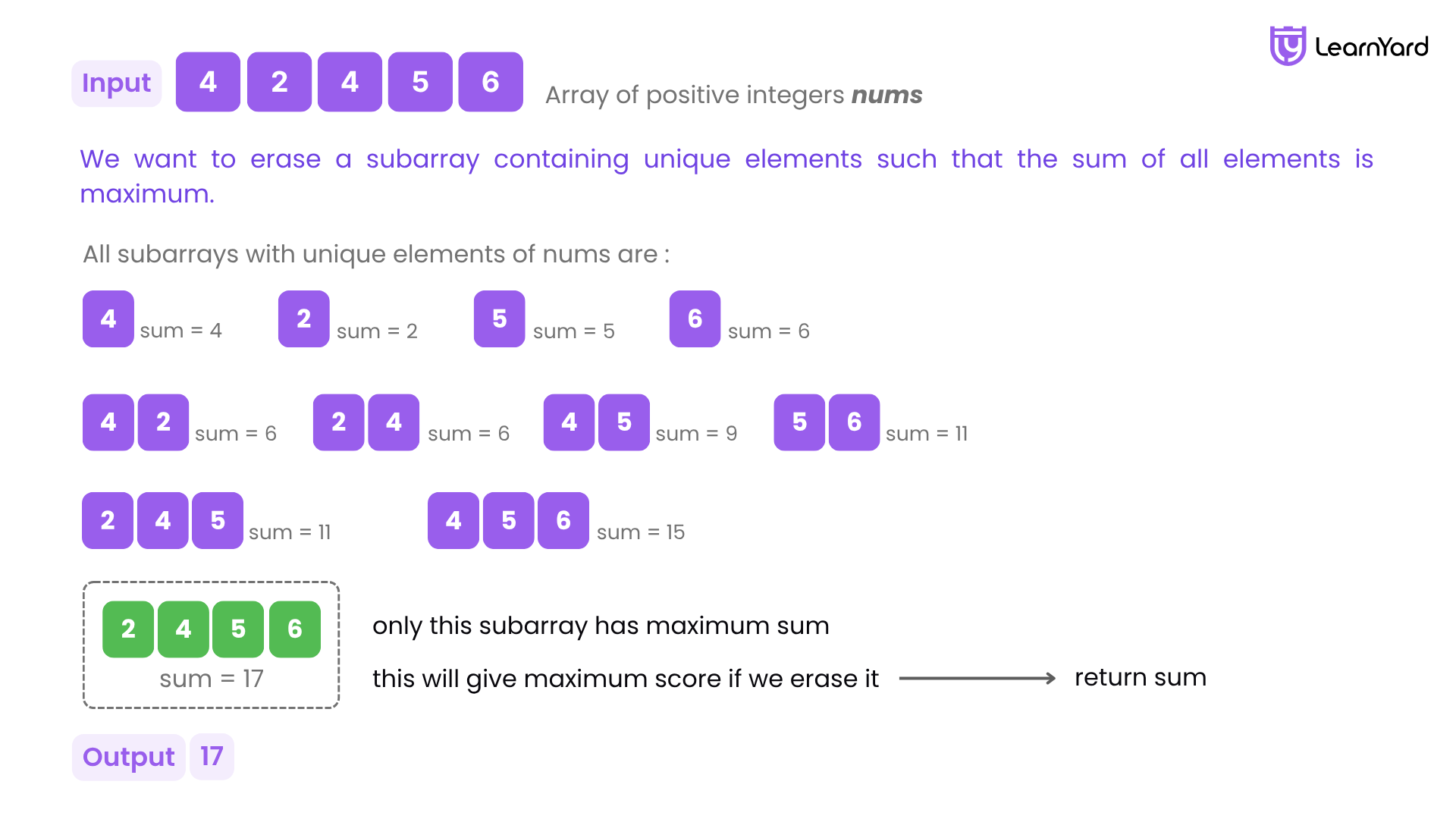
Example
Input: nums = [4,2,4,5,6]
Output: 17
Explanation: The optimal subarray here is [2,4,5,6].
Input: nums = [5,2,1,2,5,2,1,2,5]
Output: 8
Explanation: The optimal subarray here is [5,2,1] or [1,2,5].
Constraints
- 1 <= nums.length <= 10^5
- 1 <= nums[i] <= 10^4
Let's tackle the problem “Maximum Erasure Value” step by step. We'll start by understanding the most intuitive solution and then work our way toward a more optimized approach, if one exists. So, grab a pen and paper, and let's break down the algorithm together!
Brute Force Approach
Intuition
If we break down this problem, we are given an array nums consisting of positive integers. The task is to find the maximum sum of any subarray that contains only unique elements.
Now, if we observe carefully, we realize that the challenge is to find the contiguous subarray where:
- All elements are distinct (no duplicates)
- And the sum of elements is maximized
So, the first idea that comes to our mind is:
Why don’t we try checking every possible subarray and for each one, verify if all elements are unique?
If they are, calculate the sum and compare it with the current maximum.
This makes sense because:
- A brute force solution can explore all subarrays by picking every starting index and expanding forward.
- During this process, if we encounter a duplicate, we stop that subarray (as it violates the uniqueness condition).
- For every valid (unique) subarray found, we compute its sum and keep track of the maximum.
Let’s illustrate this with an example:
nums = [4, 2, 1, 2, 5, 3]
We start from index 0:
- Subarray: [4] → unique → sum = 4
- Subarray: [4, 2] → unique → sum = 6
- Subarray: [4, 2, 1] → unique → sum = 7
- Subarray: [4, 2, 1, 2] → contains duplicate 2 → stop here
Start from index 1:
- Subarray: [2] → unique → sum = 2
- Subarray: [2, 1] → unique → sum = 3
- Subarray: [2, 1, 2] → duplicate → stop
Start from index 2:
- Subarray: [1], [1, 2], [1, 2, 5], [1, 2, 5, 3] → all unique → sum = 11
Maximum sum of unique subarray = 11
So if we do this for every starting point, we’ll eventually find the maximum erasure value.
But there is one important edge case we must handle:
What if the array contains all unique elements already?
Example:
nums = [1, 2, 3, 4]
In this case:
- Any subarray of the full array is valid
- The entire array itself is the longest unique subarray → sum = 10
Therefore:
- If no duplicates appear during traversal, we should still compute the full sum of that subarray.
- We must ensure we don’t stop early just because the array is already optimal.
Maximum Erasure Value Algorithm
Step 1: Initialize Variables
- Create an integer ans = 0 to store the final result (maximum sum of unique subarray).
- Create an integer n = nums.length for easier access to array size.
Step 2: Try Every Starting Index
- Loop through each index i from 0 to n - 1:
- Create a HashSet<Integer> set to store unique elements in the current subarray.
- Initialize currSum = 0 to store the sum of current unique subarray.
Step 3: Expand the Subarray from i
- Loop through each index j from i to n - 1:
- If nums[j] is not in the set:
- Add nums[j] to set.
- Add nums[j] to currSum.
- Update ans = max(ans, currSum).
- Else (duplicate found):
- Break the inner loop (this subarray is no longer valid).
- If nums[j] is not in the set:
Step 4: Return the Result
- After checking all possible unique subarrays:
- Return ans as the maximum erasure value (i.e., the maximum sum of a unique-elements subarray).
Dry-Run
Input : nums = [4, 2, 1, 2, 5, 3]
Step 1: Initialize Variables:
ans = 0 (to store the maximum unique subarray sum)
n = nums.length = 6
Step 2: Try Every Starting Index
First Iteration (i = 0)
- Initialize set = {}, currSum = 0
Loop j from 0 to 5:
- j = 0 → nums[0] = 4 → not in set → add to set → currSum = 4 → ans = 4
- j = 1 → nums[1] = 2 → add → currSum = 6 → ans = 6
- j = 2 → nums[2] = 1 → add → currSum = 7 → ans = 7
- j = 3 → nums[3] = 2 → duplicate → break
Result from i = 0 → subarray [4, 2, 1] → sum = 7 → ans = 7
Second Iteration (i = 1)
- set = {}, currSum = 0
Loop j:
- j = 1 → nums[1] = 2 → add → currSum = 2 → ans = 7
- j = 2 → nums[2] = 1 → add → currSum = 3 → ans = 7
- j = 3 → nums[3] = 2 → duplicate → break
Result from i = 1 → subarray [2, 1] → sum = 3 → ans = 7
Third Iteration (i = 2)
- set = {}, currSum = 0
Loop j:
- j = 2 → nums[2] = 1 → add → currSum = 1 → ans = 7
- j = 3 → nums[3] = 2 → add → currSum = 3 → ans = 7
- j = 4 → nums[4] = 5 → add → currSum = 8 → ans = 8
- j = 5 → nums[5] = 3 → add → currSum = 11 → ans = 11
Result from i = 2 → subarray [1, 2, 5, 3] → sum = 11 → ans = 11
Fourth Iteration (i = 3)
- set = {}, currSum = 0
Loop j:
- j = 3 → nums[3] = 2 → add → currSum = 2 → ans = 11
- j = 4 → nums[4] = 5 → add → currSum = 7 → ans = 11
- j = 5 → nums[5] = 3 → add → currSum = 10 → ans = 11
Result from i = 3 → subarray [2, 5, 3] → sum = 10 → ans = 11
Fifth Iteration (i = 4)
- set = {}, currSum = 0
Loop j:
- j = 4 → nums[4] = 5 → add → currSum = 5 → ans = 11
- j = 5 → nums[5] = 3 → add → currSum = 8 → ans = 11
Result from i = 4 → subarray [5, 3] → sum = 8 → ans = 11
Sixth Iteration (i = 5)
- set = {}, currSum = 0
Loop j:
- j = 5 → nums[5] = 3 → add → currSum = 3 → ans = 11
Result from i = 5 → subarray [3] → sum = 3 → ans = 11
Final Step: Return the Result
Return ans = 11
Maximum Erasure Value Solution
Now lets checkout the Maximum Erasure Value in C++ , Java, Python and JavaScript.
"Maximum Erasure Value" Code in all Languages.
1.Maximum Erasure Value solution in C++ Try on Compiler
#include <iostream>
#include <unordered_set>
#include <vector>
using namespace std;
// Function to calculate the maximum sum of a subarray with unique elements
int maximumUniqueSubarray(vector<int>& nums) {
int ans = 0; // Stores the maximum sum found
int n = nums.size();
// Try every starting index i
for (int i = 0; i < n; i++) {
unordered_set<int> st; // Set to store unique elements
int currSum = 0; // Sum of the current subarray
// Extend the subarray from index i to j
for (int j = i; j < n; j++) {
if (st.count(nums[j])) break; // Stop if duplicate found
st.insert(nums[j]); // Add to set
currSum += nums[j]; // Add value to current sum
ans = max(ans, currSum); // Update result if this sum is greater
}
}
return ans;
}
int main() {
int n;
cin >> n; // Read the number of elements
vector<int> nums(n);
for (int i = 0; i < n; i++) {
cin >> nums[i]; // Read the elements of the array
}
cout << maximumUniqueSubarray(nums) << endl; // Output the result
return 0;
}2. Maximum Erasure Value Solution in Java Try on Compiler
import java.util.*;
public class Main {
// Function to return the maximum sum of a subarray with unique elements
public static int maximumUniqueSubarray(int[] nums) {
int ans = 0;
int n = nums.length;
// Try every starting index
for (int i = 0; i < n; i++) {
Set<Integer> set = new HashSet<>(); // Track unique elements
int currSum = 0;
// Expand the subarray
for (int j = i; j < n; j++) {
if (set.contains(nums[j])) break; // Duplicate found, stop
set.add(nums[j]); // Add to set
currSum += nums[j]; // Add to sum
ans = Math.max(ans, currSum); // Update answer
}
}
return ans;
}
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt(); // Read number of elements
int[] nums = new int[n];
for (int i = 0; i < n; i++) {
nums[i] = sc.nextInt(); // Read elements
}
System.out.println(maximumUniqueSubarray(nums)); // Print result
}
}
3. Maximum Erasure Value Solution in Python Try on Compiler
# Function to return the maximum sum of subarray with unique elements
def maximumUniqueSubarray(nums):
ans = 0 # Final result
n = len(nums)
# Try every starting index
for i in range(n):
seen = set() # To store unique elements in current subarray
curr_sum = 0 # To store sum of current subarray
# Expand the subarray starting from i
for j in range(i, n):
if nums[j] in seen:
break # Stop if duplicate found
seen.add(nums[j])
curr_sum += nums[j]
ans = max(ans, curr_sum) # Update max sum if current is greater
return ans
if __name__ == "__main__":
n = int(input()) # Read number of elements
nums = list(map(int, input().split())) # Read list elements
print(maximumUniqueSubarray(nums)) # Print the result
4. Maximum Erasure Value solution in JavaScript Try on Compiler
process.stdin.resume();
process.stdin.setEncoding('utf8');
let input = '';
process.stdin.on('data', function (chunk) {
input += chunk;
});
process.stdin.on('end', function () {
// Split input into lines and parse numbers
const lines = input.trim().split('\n');
const n = parseInt(lines[0]); // First line is the size
const nums = lines[1].split(' ').map(Number); // Second line is the array
console.log(maximumUniqueSubarray(nums)); // Output result
});
function maximumUniqueSubarray(nums) {
let ans = 0;
let n = nums.length;
for (let i = 0; i < n; i++) {
const set = new Set(); // Set to track unique elements
let currSum = 0;
for (let j = i; j < n; j++) {
if (set.has(nums[j])) break; // Stop if duplicate found
set.add(nums[j]);
currSum += nums[j];
ans = Math.max(ans, currSum); // Update result
}
}
return ans;
}
Maximum Erasure Value Complexity Analysis
Time Complexity: O(n^2)
Initial Input Reading Loop: O(n)
- The code reads n elements from input.
- This takes linear time with respect to the size of the array.
- Time: O(n)
Outer Loop (Try Every Starting Index): O(n)
- We loop over each possible starting index i from 0 to n - 1.
- So the outer loop runs n times.
- Time: O(n)
Inner Loop (Expand Subarray Until Duplicate): O(n)
- For each starting index i, we try to extend the subarray to the right until we hit a duplicate.
- In the worst case (all unique values), the inner loop also runs up to n times.
- Important Note:
The Set is used for constant-time duplicate checks and insertions (O(1) on average per operation),
but since each inner loop may run up to n steps, its overall contribution is O(n) per outer iteration. - Time: O(n)
Total Work Done: O(n^2)
- Outer loop runs n times
- Inner loop runs O(n) each time
- So total time = O(n) * O(n) = O(n²)
Final Time Complexity: O(n²)
Space Complexity: O(n)
Auxiliary Space Complexity: O(n)
This refers to any extra space used by the algorithm, excluding the input and output space.
In this approach, we use:
- A Set to store unique elements during each subarray iteration → can grow up to size n
- A few integer variables (ans, currSum, i, j)
Since the Set size depends on the number of elements (in the worst case all elements are unique),
the auxiliary space used is O(n).
Input Space: O(n)
- The input array nums contains n integers → occupies O(n) space.
Output Space: O(1)
- The function returns a single integer value (the max erasure value).
- This takes constant space → O(1).
Total Space Complexity: O(n)
Combining all the components:
- Input array: O(n)
- Output value: O(1)
- Extra space used (set + variables): O(n)
Total Space Complexity = O(n) + O(1) + O(n) = O(n)
Optimal Approach
Intuition
In the brute force approach, we fix a starting index i and expand the subarray to the right (j) until we hit a duplicate. At every step, we check if the current subarray contains only unique elements, and if so, we compute the sum and track the maximum.
This involves nested loops—an outer loop over all possible starts, and an inner loop to grow the subarray until it breaks.
This gives us O(n²) time complexity, which is inefficient for large inputs.
So what are we really doing with brute force?
We’re trying to find the maximum sum of a subarray that contains only unique elements.
But notice something:
In brute force, we’re restarting the subarray every time we find a duplicate — even if the duplicate was far back. What if we could reuse part of the already checked subarray instead of starting over?
Instead of starting fresh every time like brute force, what if we slide a window over the array and maintain a set of unique elements?
That way:
- We expand the window to the right as long as the elements are unique.
- If we hit a duplicate, we shrink the window from the left until the duplicate is removed.
- We keep track of the sum dynamically as the window grows or shrinks.
This reduces the time complexity to O(n) because each element is inserted and removed from the set at most once.
Maximum Erasure Value Algorithm
Step 1: Initialize Variables
- Create an empty set seen to store the current unique elements in the window.
- Initialize two pointers:
- left = 0 → start of the sliding window
- right = 0 → end of the sliding window
- Initialize two integers:
- currSum = 0 → sum of current window
- ans = 0 → to store the maximum sum found so far
Step 2: Slide the Window
- While right < n, repeat:
- If nums[right] is not in seen:
- Add nums[right] to the seen set.
- Add nums[right] to currSum.
- Update ans = max(ans, currSum).
- Increment right by 1 to expand the window.
- Else (duplicate element found):
- While nums[right] is already in seen:
- Remove nums[left] from the seen set.
- Subtract nums[left] from currSum.
- Increment left by 1 to shrink the window.
- While nums[right] is already in seen:
- If nums[right] is not in seen:
Step 3: Return the Result
- After the loop ends, return ans as the final answer.
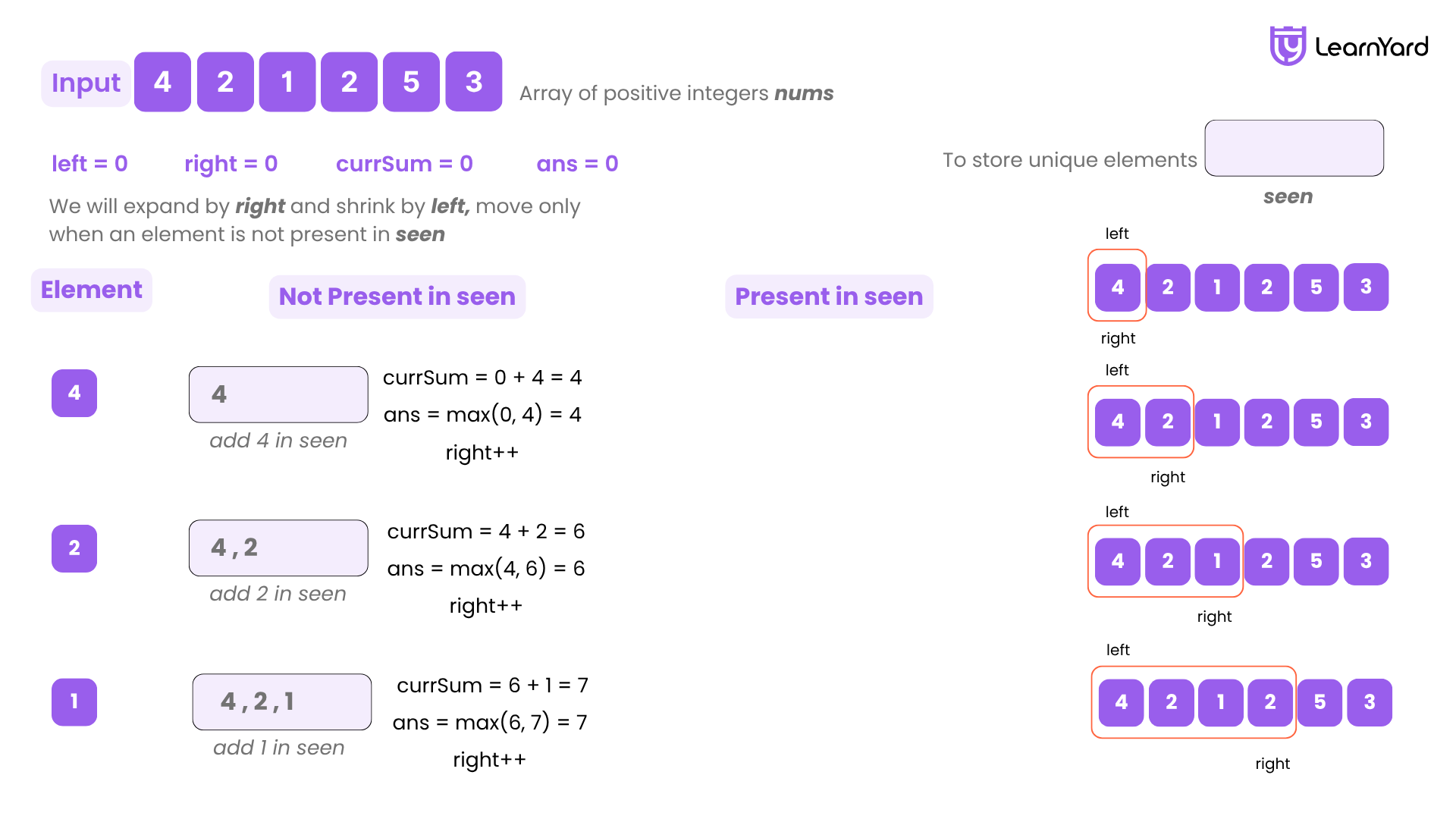
Dry-Run
Input: nums = [4, 2, 1, 2, 5, 3]
Step 1: Initialize Variables
left = 0
right = 0
seen = {} # Set to store unique elements
currSum = 0
ans = 0
Step 2: Traverse the Array Using Sliding Window
First Iteration (right = 0)
nums[0] = 4
- 4 is not in seen
- Add 4 to seen → seen = {4}
- Update currSum = 0 + 4 = 4
- Update ans = max(0, 4) = 4
- Increment right → right = 1
Second Iteration (right = 1)
nums[1] = 2
- 2 is not in seen
- Add 2 → seen = {2, 4}
- Update currSum = 4 + 2 = 6
- Update ans = max(4, 6) = 6
- Increment right → right = 2
Third Iteration (right = 2)
nums[2] = 1
- 1 is not in seen
- Add 1 → seen = {1, 2, 4}
- Update currSum = 6 + 1 = 7
- Update ans = max(6, 7) = 7
- Increment right → right = 3
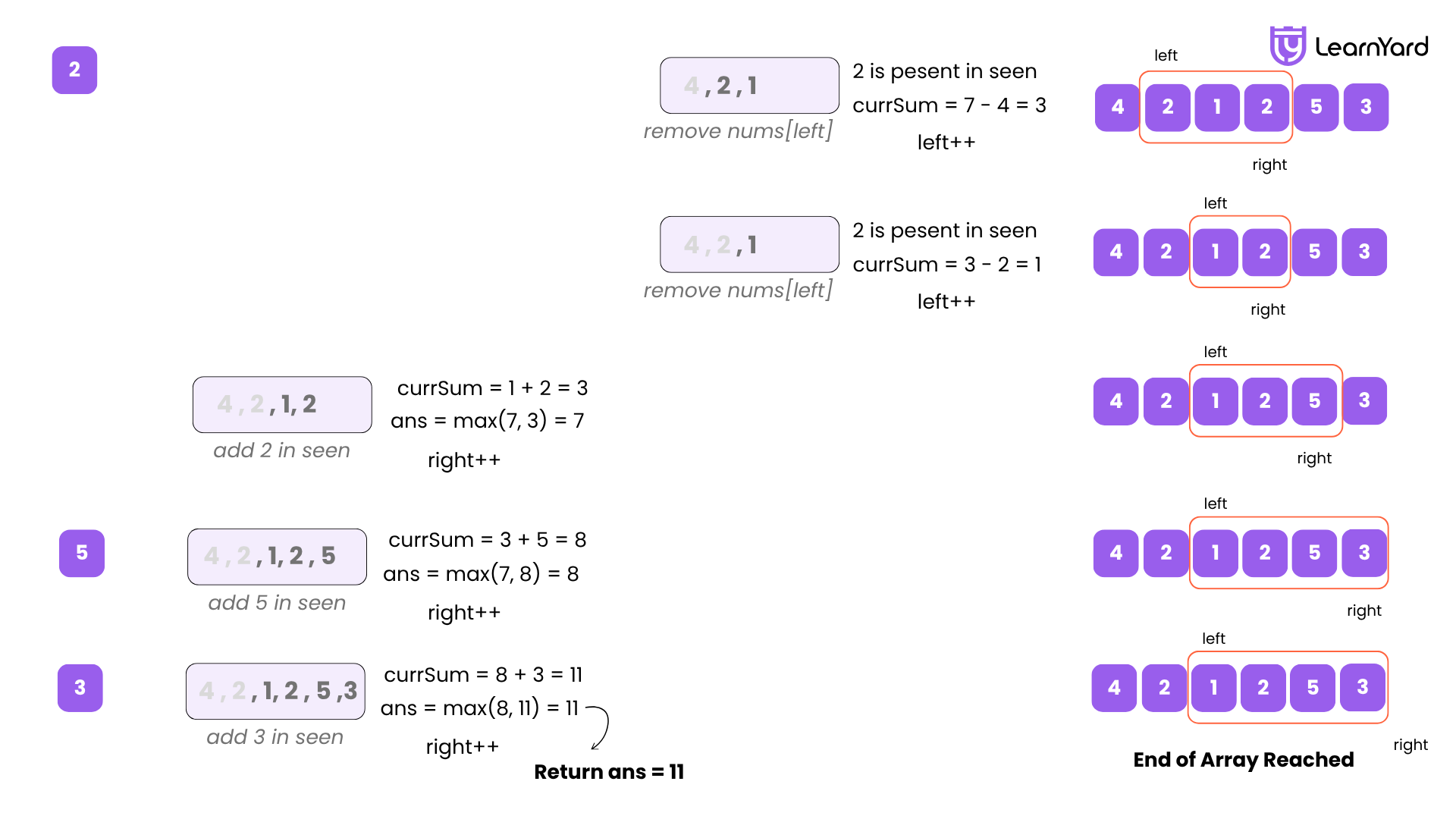
Fourth Iteration (right = 3)
nums[3] = 2
- 2 is already in seen
- Start shrinking window from the left until 2 is removed:
- Remove nums[0] = 4 → seen = {1, 2} → currSum = 7 - 4 = 3 → left = 1
- Remove nums[1] = 2 → seen = {1} → currSum = 3 - 2 = 1 → left = 2
- Now 2 is not in seen
- Add 2 → seen = {1, 2}
- Update currSum = 1 + 2 = 3
- ans = max(7, 3) = 7 (no change)
- Increment right → right = 4
Fifth Iteration (right = 4)
nums[4] = 5
- 5 is not in seen
- Add 5 → seen = {1, 2, 5}
- Update currSum = 3 + 5 = 8
- Update ans = max(7, 8) = 8
- Increment right → right = 5
Sixth Iteration (right = 5)
nums[5] = 3
- 3 is not in seen
- Add 3 → seen = {1, 2, 3, 5}
- Update currSum = 8 + 3 = 11
- Update ans = max(8, 11) = 11
- Increment right → right = 6
Step 3: End of Array Reached
- Final right = 6 → loop ends
Step 4: Return the Result
- Return ans = 11
Final Output: 11
Maximum Erasure Value Solution
Now lets checkout the Maximum Erasure Valuelet's check out code in C++, Java, Python, and JavaScript.
Maximum Erasure Value Code in all Languages.
1. Maximum Erasure Value solution in C++ Try on Compiler
#include <iostream>
#include <unordered_set>
#include <vector>
using namespace std;
int maximumUniqueSubarray(vector<int>& nums) {
unordered_set<int> seen; // To store unique elements
int left = 0, right = 0;
int currSum = 0, ans = 0;
while (right < nums.size()) {
if (seen.find(nums[right]) == seen.end()) {
// Unique element → expand window
seen.insert(nums[right]);
currSum += nums[right];
ans = max(ans, currSum);
right++;
} else {
// Duplicate found → shrink window
seen.erase(nums[left]);
currSum -= nums[left];
left++;
}
}
return ans;
}
int main() {
int n;
cin >> n; // Input size
vector<int> nums(n);
for (int i = 0; i < n; i++)
cin >> nums[i]; // Input array elements
cout << maximumUniqueSubarray(nums); // Output result
return 0;
}
2. Maximum Erasure Value Solution in Java Try on Compiler
import java.util.*;
public class Main {
public static int maximumUniqueSubarray(int[] nums) {
Set<Integer> seen = new HashSet<>(); // To store unique elements
int left = 0, right = 0;
int currSum = 0, ans = 0;
while (right < nums.length) {
if (!seen.contains(nums[right])) {
// Unique element → expand window
seen.add(nums[right]);
currSum += nums[right];
ans = Math.max(ans, currSum);
right++;
} else {
// Duplicate → shrink window
seen.remove(nums[left]);
currSum -= nums[left];
left++;
}
}
return ans;
}
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt(); // Input size
int[] nums = new int[n];
for (int i = 0; i < n; i++)
nums[i] = sc.nextInt(); // Input array
System.out.print(maximumUniqueSubarray(nums)); // Output result
}
}
3. Maximum Erasure Value Solution in Python Try on Compiler
def maximumUniqueSubarray(nums):
seen = set() # To store unique elements
left = 0
curr_sum = 0
ans = 0
for right in range(len(nums)):
while nums[right] in seen:
# Remove from window until duplicate is gone
seen.remove(nums[left])
curr_sum -= nums[left]
left += 1
seen.add(nums[right])
curr_sum += nums[right]
ans = max(ans, curr_sum)
return ans
# Input from user
n = int(input()) # Size of array
nums = list(map(int, input().split())) # Space-separated integers
print(maximumUniqueSubarray(nums)) # Output result
4. Maximum Erasure Value solution in JavaScript Try on Compiler
function maximumUniqueSubarray(nums) {
const seen = new Set(); // To store unique elements in current window
let left = 0;
let currSum = 0;
let ans = 0;
for (let right = 0; right < nums.length; right++) {
// If current number is already in window, shrink from left
while (seen.has(nums[right])) {
seen.delete(nums[left]);
currSum -= nums[left];
left++;
}
// Add current number to window
seen.add(nums[right]);
currSum += nums[right];
ans = Math.max(ans, currSum); // Update max sum
}
return ans;
}
// Reading input from user
const readline = require('readline');
const rl = readline.createInterface({
input: process.stdin,
output: process.stdout
});
let inputLines = [];
rl.on('line', (line) => {
inputLines.push(line.trim());
if (inputLines.length === 2) {
const n = parseInt(inputLines[0]); // Size of array
const nums = inputLines[1].split(' ').map(Number); // Array elements
console.log(maximumUniqueSubarray(nums)); // Output result
rl.close();
}
});
Maximum Erasure Value Complexity Analysis
Time Complexity: O(n)
Outer Loop: O(n)
The main loop runs from right = 0 to right = n - 1.
Let’s denote:
n = number of elements in the input array
So, the outer loop executes n times, which is O(n).
Inner While Loop: O(n)
The inner while (seen.has(nums[right])) loop shrinks the window from the left.
Although it appears nested, the left pointer only moves forward and never backtracks.
Each element is added to the set once and removed at most once.
Therefore, the total number of operations in both loops combined is linear — O(n).
Input Reading Loop: O(n)
Reading n elements from input takes O(n) time.
Final Time Complexity: O(n)
We perform O(1) operations for each element, and both pointers (left and right) move across the array at most once.
So, the total time complexity is: O(n)
Where:
n is the number of elements in the input array.
Space Complexity: O(n)
Auxiliary Space Complexity: O(n)
This refers to any extra space used by the algorithm that is independent of the input and output space.
In this approach, we use:
- A Set to store unique elements in the current window → can grow up to size n in worst case
Hence, the extra space used is O(n).
Total Space Complexity: O(n)
This includes the space required for:
- Input space: The input array of length n → O(n)
- Output space: A single integer is returned → O(1)
- Extra space used by the algorithm: A Set to store elements → O(n)
Combining all the space requirements:
Total Space Complexity = O(n) (input) + O(n) (set) + O(1) (variables + output) = O(n)
Where:
n is the number of elements in the input array.
Similar Problems
Given a string s, find the length of the longest substring without duplicate characters.