Maximum Bags With Full Capacity of Rocks Solution In C++/Java/Python/JS
Problem Description
You have n bags numbered from 0 to n - 1. You are given two 0-indexed integer arrays capacity and rocks. The ith bag can hold a maximum of capacity[i] rocks and currently contains rocks[i] rocks. You are also given an integer additionalRocks, the number of additional rocks you can place in any of the bags.
Return the maximum number of bags that could have full capacity after placing the additional rocks in some bags.
Example
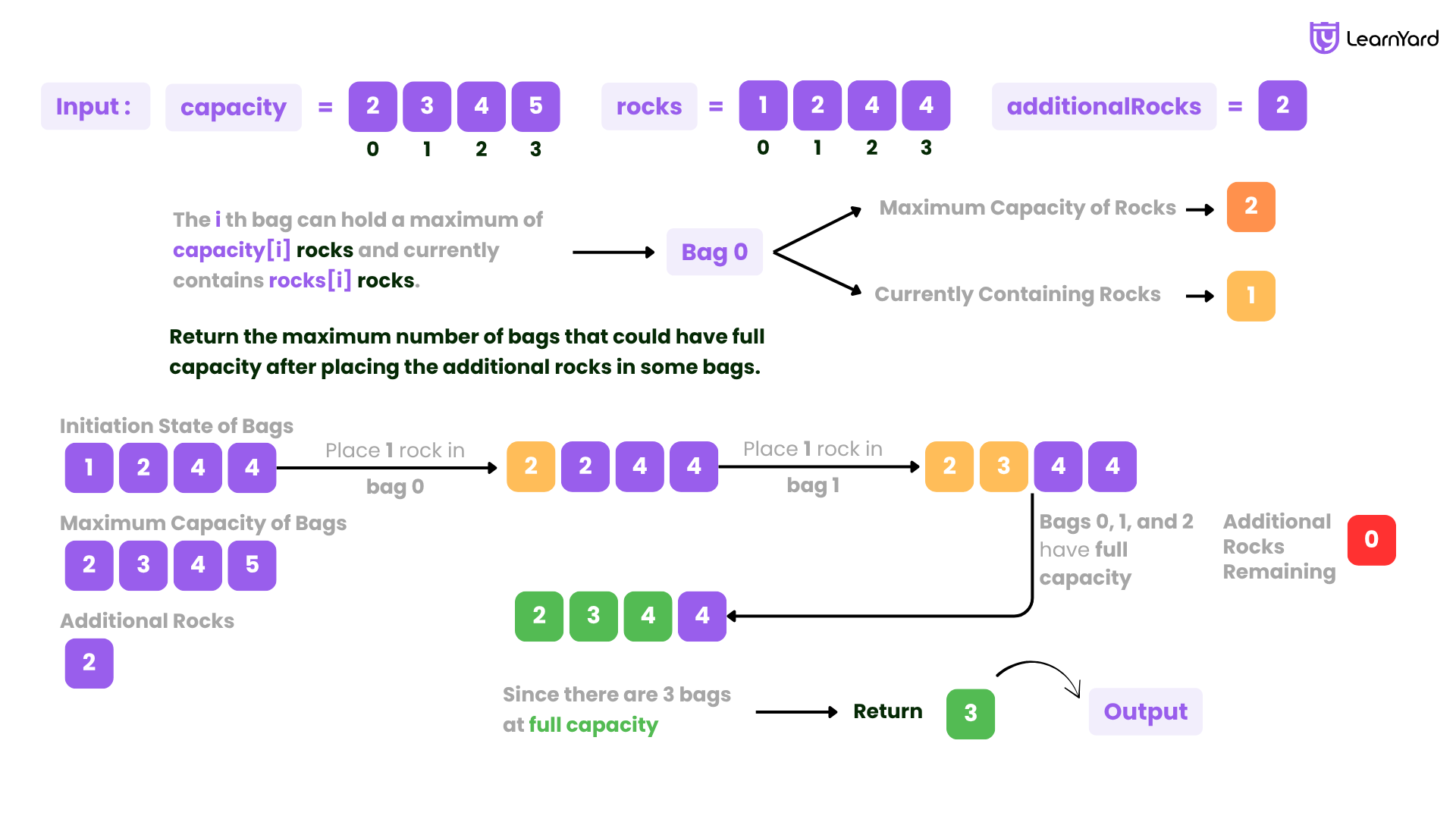
Input: capacity = [2,3,4,5], rocks = [1,2,4,4], additionalRocks = 2
Output: 3
Explanation:
Place 1 rock in bag 0 and 1 rock in bag 1.
The number of rocks in each bag are now [2,3,4,4].
Bags 0, 1, and 2 have full capacity.
There are 3 bags at full capacity, so we return 3.
It can be shown that it is not possible to have more than 3 bags at full capacity.
Note that there may be other ways of placing the rocks that result in an answer of 3.
Input: capacity = [10,2,2], rocks = [2,2,0], additionalRocks = 100
Output: 3
Explanation:
Place 8 rocks in bag 0 and 2 rocks in bag 2.
The number of rocks in each bag are now [10,2,2].
Bags 0, 1, and 2 have full capacity.
There are 3 bags at full capacity, so we return 3.
It can be shown that it is not possible to have more than 3 bags at full capacity.
Note that we did not use all of the additional rocks.
Constraints
- n == capacity.length == rocks.length
- 1 <= n <= 5 * 104
- 1 <= capacity[i] <= 109
- 0 <= rocks[i] <= capacity[i]
- 1 <= additionalRocks <= 109
Figuring out "Maximum Bags With Full Capacity of Rocks solution" can be solved using different approaches. We will first figure out the most intuitive approach and move to the optimal approach if exists. Let's sit with a pen and paper and figure out the algorithm !!
Optimal Approach
Intuition
We have a set of n bags, each with a certain capacity. Some of these bags already contain rocks, and we are given a limited number of "additionalRocks" that we can distribute. Our goal is to maximize the number of bags that reach full capacity.
How do you think we should approach this problem? Maybe we should just distribute the rocks evenly among all the bags?
That sounds reasonable at first! But let’s test that idea with a small example.
Suppose we have:
capacity = [5, 3, 7]
rocks = [4, 2, 3]
additionalRocks = 4
So we have three bags:
- Bag 0 has a capacity of 5 but currently holds 4 rocks.
- Bag 1 has a capacity of 3 but currently holds 2 rocks.
- Bag 2 has a capacity of 7 but currently holds 3 rocks.
Now, if we spread the rocks evenly, we might give 1 rock to each bag, but does that seem like the best approach? Actually, no. Some bags need way more rocks than others to be full. What If we focus on the ones that are almost full ?
We can complete them quickly!
Exactly! So let’s shift our approach.
Instead of randomly distributing rocks, let’s first determine how many rocks each bag needs to reach full capacity.
For each bag, we can calculate
"needed_rocks = capacity[i] - rocks[i]"
So in our example:
- Bag 0 needs 1 rock (5 - 4 = 1).
- Bag 1 needs 1 rock (3 - 2 = 1).
- Bag 2 needs 4 rocks (7 - 3 = 4).
Which bags should we prioritize?
Shall we focus on the ones that need the fewest rocks first, because they can be completed with minimal effort!
Exactly! That means we should fill the bags that need the least number of rocks first.
To do this, let’s sort the needed_rocks list in ascending order:
needed_rocks = [1, 1, 4]
Now, we go step by step:
Fill Bag 0 (needs 1 rock) → We use 1 rock, and now we have additionalRocks = 3 left.
Fill Bag 1 (needs 1 rock) → We use another rock, and now we have additionalRocks = 2 left.
Bag 2 needs 4 rocks, but we only have 2 left, so we can’t fully fill it.
At this point, we have 2 fully filled bags.
- Did we always make the best choice at every step?
- Were we looking ahead, or were we making a decision based on what seemed best in the moment?
We always picked the bag that needed the fewest rocks, without thinking about the others. So, we were making a decision at every step that seemed best at that moment.
That’s the definition of a greedy approach—we always make the best local decision at each step.
Oh! So the greedy choice here was to fill the smallest gaps first, since that gave us the most fully-filled bags.
Let's now see how our algorithm looks like!!
Maximum Bags With Full Capacity of Rocks Algorithm
- Compute how many rocks each bag needs to be full.
- Sort the bags based on how many rocks they need (smallest to largest).
- Start filling the bags in this order until we run out of additionalRocks.
- Count how many bags we successfully filled.
That makes a lot of sense! But how to code up this approach?
Approach
Step 1: Calculate Remaining Capacity
- For each bag, compute how many more rocks are needed to fill it completely by subtracting the current number of rocks from its capacity.
- Store these values in a new list.
Step 2: Sort the List
- Sort the list of remaining capacities in ascending order.
- This ensures that bags requiring the fewest rocks are prioritized.
Step 3: Fill the Bags Greedily
- Initialize a counter to track the number of completely filled bags.
- Iterate through the sorted list:
- If the current bag can be filled with the available rocks, fill it, increase the counter, and decrease the available rock count accordingly.
- If the remaining rocks are insufficient to fill the next bag, stop the process.
Step 4: Return the Result: Return the count of completely filled bags.
Let us understand this with a video,
Dry-Run
Sample Input
capacity = [5, 8, 7, 6, 4]
rocks = [3, 5, 3, 6, 2]
additionalRocks = 5
Output:- 3
Step 1: Calculate Remaining Capacity
- For each bag: remaining = capacity[i] - rocks[i]
- Result: remainingCapacity = [2, 3, 4, 0, 2]
Step 2: Sort the Remaining Capacity
- Before sort: [2, 3, 4, 0, 2]
- After sort: [0, 2, 2, 3, 4]
Step 3: Fill Bags Using Additional Rocks
- Start with:
- maxFilledBags = 0
- additionalRocks = 5
- Loop through remainingCapacity:
1. 0 rocks needed:
- ✅ 0 ≤ 5 → fill it
- ➕ maxFilledBags = 1
- ➖ additionalRocks = 5 - 0 = 5
2. 2 rocks needed:
- ✅ 2 ≤ 5 → fill it
- ➕ maxFilledBags = 2
- ➖ additionalRocks = 5 - 2 = 3
3. 2 rocks needed:
- ✅ 2 ≤ 3 → fill it
- ➕ maxFilledBags = 3
- ➖ additionalRocks = 3 - 2 = 1
4. 3 rocks needed
❌ 3 > 1 → cannot fill, break loop
Final Output: return maxFilledBags = 3
Maximum Bags With Full Capacity of Rocks Solution
Now, let's checkout the Maximum Bags With Full Capacity of Rocks in c++, Java, Python and JavaScript
"Maximum Bags With Full Capacity of Rocks" Code in all Languages.
1. Maximum Bags With Full Capacity of Rocks solution in C++ Try on Compiler
class Solution {
public:
int maximumBags(vector<int>& capacity, vector<int>& rocks, int additionalRocks) {
// Get the number of bags
int numBags = capacity.size();
// Create an array to store the remaining capacity of each bag
vector<int> remainingCapacity(numBags);
// Calculate the remaining capacity for each bag
for (int i = 0; i < numBags; ++i) {
remainingCapacity[i] = capacity[i] - rocks[i];
}
// Sort the remaining capacities in ascending order
sort(remainingCapacity.begin(), remainingCapacity.end());
// Variable to count the number of completely filled bags
int maxFilledBags = 0;
// Iterate through the sorted remaining capacities
for (int requiredRocks : remainingCapacity) {
// If we have enough additional rocks to fill this bag
if (requiredRocks <= additionalRocks) {
// Increase the count of completely filled bags
maxFilledBags++;
// Deduct the used rocks from additionalRocks
additionalRocks -= requiredRocks;
} else {
// If we can't fill the current bag, break out of the loop
break;
}
}
// Return the number of completely filled bags
return maxFilledBags;
}
};2. Maximum Bags With Full Capacity of Rocks Solution in Java Try on Compiler
class Solution {
public int maximumBags(int[] capacity, int[] rocks, int additionalRocks) {
// Get the number of bags
int numBags = capacity.length;
// Create an array to store the remaining capacity of each bag
int[] remainingCapacity = new int[numBags];
// Calculate the remaining capacity for each bag
for (int i = 0; i < numBags; ++i) {
remainingCapacity[i] = capacity[i] - rocks[i];
}
// Sort the remaining capacities in ascending order
Arrays.sort(remainingCapacity);
// Variable to count the number of completely filled bags
int maxFilledBags = 0;
// Iterate through the sorted remaining capacities
for (int requiredRocks : remainingCapacity) {
// If we have enough additional rocks to fill this bag
if (requiredRocks <= additionalRocks) {
// Increase the count of completely filled bags
maxFilledBags++;
// Deduct the used rocks from additionalRocks
additionalRocks -= requiredRocks;
} else {
// If we can't fill the current bag, break out of the loop
break;
}
}
// Return the number of completely filled bags
return maxFilledBags;
}
}
3. Maximum Bags With Full Capacity of Rocks Solution in Python Try on Compiler
class Solution:
def maximumBags(self, capacity, rocks, additionalRocks):
# Calculate the remaining capacity for each bag
remaining_capacity = [capacity[i] - rocks[i] for i in range(len(capacity))]
# Sort the remaining capacities in ascending order
remaining_capacity.sort()
# Variable to count the number of completely filled bags
max_filled_bags = 0
# Iterate through the sorted remaining capacities
for required_rocks in remaining_capacity:
# If we have enough additional rocks to fill this bag
if required_rocks <= additionalRocks:
# Increase the count of completely filled bags
max_filled_bags += 1
# Deduct the used rocks from additionalRocks
additionalRocks -= required_rocks
else:
# If we can't fill the current bag, break out of the loop
break
# Return the number of completely filled bags
return max_filled_bags4. Maximum Bags With Full Capacity of Rocks solution in JavaScript Try on Compiler
class Solution {
maximumBags(capacity, rocks, additionalRocks) {
// Calculate the remaining capacity for each bag
let remainingCapacity = capacity.map((cap, i) => cap - rocks[i]);
// Sort the remaining capacities in ascending order
remainingCapacity.sort((a, b) => a - b);
// Variable to count the number of completely filled bags
let maxFilledBags = 0;
// Iterate through the sorted remaining capacities
for (let requiredRocks of remainingCapacity) {
// If we have enough additional rocks to fill this bag
if (requiredRocks <= additionalRocks) {
// Increase the count of completely filled bags
maxFilledBags++;
// Deduct the used rocks from additionalRocks
additionalRocks -= requiredRocks;
} else {
// If we can't fill the current bag, break out of the loop
break;
}
}
// Return the number of completely filled bags
return maxFilledBags;
}
}Maximum Bags With Full Capacity of Rocks Complexity Analysis
Time Complexity: O(n*logn)
Time Complexity
Computing remaining capacity → O(n)
We iterate through capacity and rocks arrays once to compute remainingCapacity.
Sorting remainingCapacity → O(nlogn)
Sorting takes O(nlogn) using a comparison-based sorting algorithm like QuickSort or MergeSort.
Filling the bags greedily → O(n)
We iterate through remainingCapacity once, processing at most nnn elements.
Total Time Complexity: O(n)+O(nlogn)+O(n)=O(nlogn)
Space Complexity: O(n)
Auxiliary Space Complexity
Auxiliary space refers to the extra space required by an algorithm other than the input space.
remainingCapacity array → O(n)
This stores the remaining space for each bag.
Sorting space → O(1)
(if in-place sorting like QuickSort is used) or O(n) (if MergeSort is used).
Total Auxiliary Space Complexity:O(n)
Total Space Complexity
- Input arrays (capacity and rocks) → O(n) (given as input, not extra space).
- Extra storage (remainingCapacity) → O(n).
- Other variables (numBags, maxFilledBags, etc.) → O(1).
Total Space Complexity: O(n)
Similar Problems
A conveyor belt has packages that must be shipped from one port to another within days days.
The ith package on the conveyor belt has a weight of weights[i]. Each day, we load the ship with packages on the conveyor belt (in the order given by weights). We may not load more weight than the maximum weight capacity of the ship.
Return the least weight capacity of the ship that will result in all the packages on the conveyor belt being shipped within days days.
You are assigned to put some amount of boxes onto one truck. You are given a 2D array boxTypes, where boxTypes[i] = [numberOfBoxesi, numberOfUnitsPerBoxi]:
- numberOfBoxesi is the number of boxes of type i.
- numberOfUnitsPerBoxi is the number of units in each box of the type i.
You are also given an integer truckSize, which is the maximum number of boxes that can be put on the truck. You can choose any boxes to put on the truck as long as the number of boxes does not exceed truckSize.
Return the maximum total number of units that can be put on the truck.