Maximum Average Subarray I Solution In C++/Java/Python/JS
Problem Description
You are given an integer array nums consisting of n elements, and an integer k.
Find a contiguous subarray whose length is equal to k that has the maximum average value and return this value. Any answer with a calculation error less than 10^-5 will be accepted.
What is a Subarray?
A subarray is a contiguous (i.e., continuous) part of an array.
This means all the elements in the subarray are next to each other in the original array, and they maintain the original order.
It’s important not to confuse a subarray with a subset, because a subset can have elements from any position, but a subarray must be unbroken, like a slice or a window of the original array.
Example
nums = [3, 5, 7, 2]
Here are some valid subarrays:
[3] → takes just the first element
[5, 7] → starts at index 1, ends at index 2
[3, 5, 7] → starts from the beginning, includes the first 3 elements
[7, 2] → starts at index 2, ends at index 3
[3, 5, 7, 2] → the entire array is also a subarray
But these are not valid subarrays:
[3, 7] → skips 5, so it's not contiguous
[5, 2] → skips 7, again not allowed
Examples
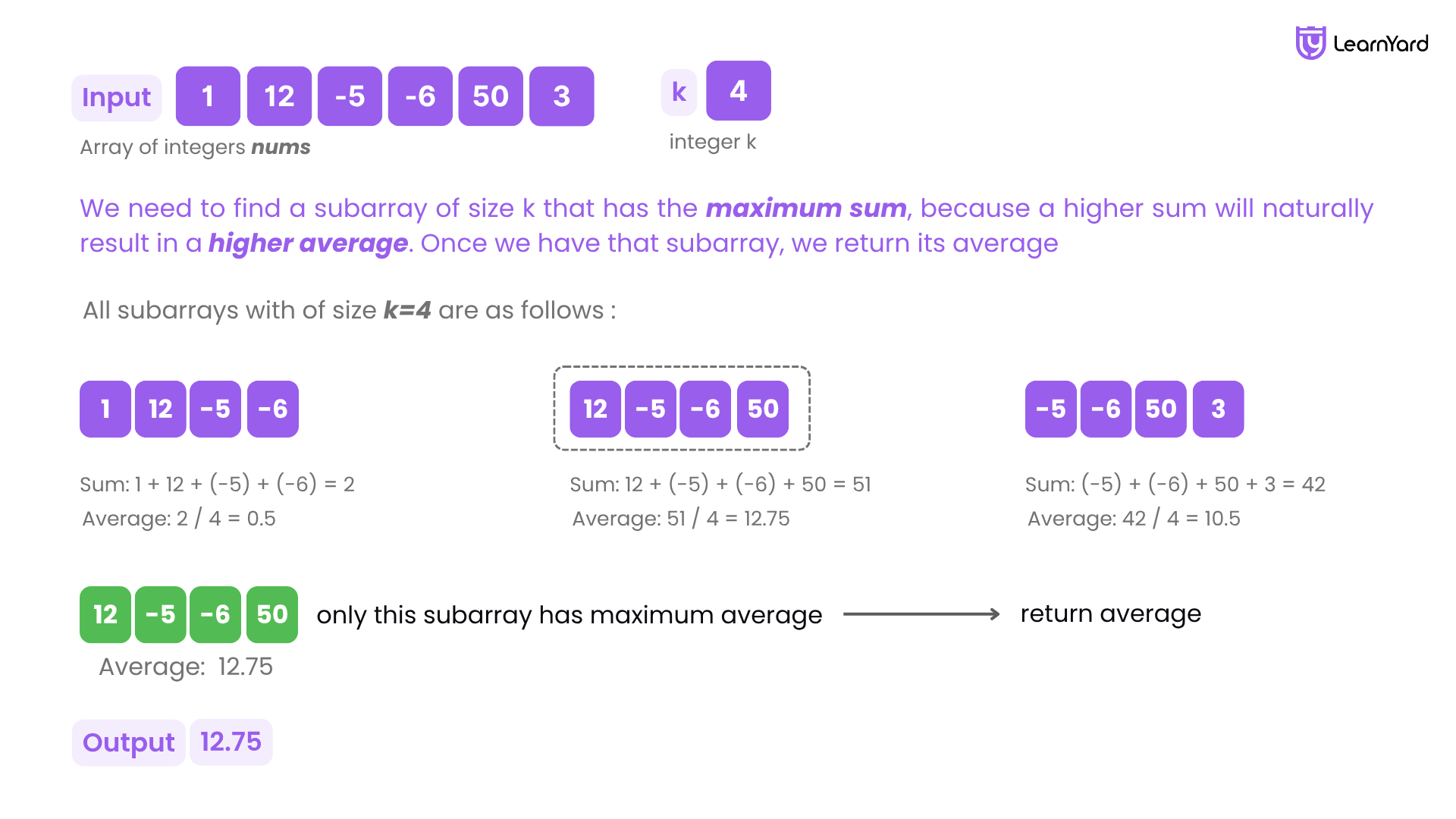
Input: nums = [1,12,-5,-6,50,3], k = 4
Output: 12.75000
Explanation: The subarray [12, -5, -6, 50] gives the maximum sum 51, so the maximum average is (12 - 5 - 6 + 50) / 4 = 51 / 4 = 12.75
Input: nums = [5], k = 1
Output: 5.00000
Explanation: With only one element and k = 1, the maximum average is simply the element itself, 5.0
Constraints
- n == nums.length
- 1 <= k <= n <= 105
- -10^4 <= nums[i] <= 10^4
The very first question that comes to our mind after reading the problem is: How can we find which subarray of length k has the maximum average? Most of us already know that one straightforward way is to check every possible subarray of size k and calculate its average. To build a solid understanding, let's start by exploring this brute-force approach in detail. This will help us grasp the core idea clearly before moving on to more optimized techniques like sliding window.
Brute-Force Approach
Intuition
We are given an array of numbers and asked to find the subarray of length k that has the highest average value. The first idea that naturally comes to our mind is to try every possible subarray of length k, calculate its average, and track the maximum one. This is a classic brute-force approach where we leave no possibility unchecked. For this, we can use a nested loop. The outer loop will fix the starting index of the subarray, and the inner loop will help us build subarrays of the same length as k from that starting point.
Generating Subarrays of Length k using Nested Loops
To implement this we’ll fix the starting index of a subarray in the outer loop, just like we did with substrings. This loop runs from i = 0 to i = nums.length - k, ensuring we only consider valid subarrays of length exactly k.
For each fixed starting index i, we use an inner loop with index j to manually collect elements from the array and calculate their sum. This inner loop runs from j = i to j < i + k. We initialize a variable sum = 0 before entering the inner loop, and for each element, we simply do sum += nums[j]. After the loop, we compute the average by dividing sum by k, and then compare it with the maximum average found so far to update our result. This manual technique helps us understand how contiguous subarrays are formed and how their sum or average can be computed step by step, similar to how we manually formed substrings character by character.
Let’s take an example to understand this clearly. Suppose nums = [1, 12, -5, -6, 50, 3] and k = 4. Here's how the subarrays are collected:
- At i = 0, the inner loop collects nums[0], nums[1], nums[2], nums[3] → subarray = [1, 12, -5, -6]
- At i = 1, the inner loop collects nums[1], nums[2], nums[3], nums[4] → subarray = [12, -5, -6, 50]
- At i = 2, the inner loop collects nums[2], nums[3], nums[4], nums[5] → subarray = [-5, -6, 50, 3]
Each subarray is of size k = 4, and we calculate its average and keep track of the maximum average found. This step-by-step construction builds strong clarity for learners who are just getting started with array operations and sliding window concepts.
Approach
Step 1: Initialize the Maximum Average
We start by initializing a variable maxAverage to a very small value (e.g., -1e9) to ensure that any valid average we calculate will be larger. This variable will keep track of the highest average found so far.
Step 2: Iterate Over All Possible Subarrays of Size k
We use an outer loop that starts from index i = 0 and runs until i = n - k, where n is the size of the input array. This loop ensures that we check every possible contiguous subarray of size k in the array.
Step 3: Calculate the Sum of Each Subarray
Inside the outer loop, we initialize a variable currentSum to 0.
We then use an inner loop from j = i to j = i + k - 1 to add up the elements of the current subarray of size k. This sum is stored in currentSum.
Step 4: Compute the Average and Update maxAverage
After calculating the sum of the current subarray, we compute its average by dividing currentSum by k.
We then compare this currentAverage with maxAverage, and if it is greater, we update maxAverage.
This step ensures that after all subarrays are checked, maxAverage holds the highest average value.
Step 5: Return the Maximum Average
After the outer loop completes (i.e., all subarrays of size k are processed), we return the value of maxAverage as the final result. This value represents the maximum average of any subarray of size k in the input array.
Dry Run
Let’s do a step-by-step dry run of the nested loop approach for the input:
nums = [1, 12, -5, -6, 50, 3], k = 4
We aim to find the maximum average of any subarray of size 4.
Step 1: Start outer loop to consider all subarrays of size k
The outer loop runs from i = 0 to i = n - k = 2 (because 6 - 4 = 2).
For each i, we calculate the sum of the next k elements using the inner loop.
Iteration i = 0
- Initialize currentSum = 0
Inner loop from j = 0 to j = 3 (i + k - 1)
- j = 0 → currentSum = 0 + 1 = 1
- j = 1 → currentSum = 1 + 12 = 13
- j = 2 → currentSum = 13 + (-5) = 8
- j = 3 → currentSum = 8 + (-6) = 2
Sum of subarray [1, 12, -5, -6] = 2
Calculate average: currentAverage = 2 / 4 = 0.5
Update maxAverage: maxAverage = max(-1e9, 0.5) = 0.5
Iteration i = 1
- Initialize currentSum = 0
Inner loop from j = 1 to j = 4
- j = 1 → currentSum = 0 + 12 = 12
- j = 2 → currentSum = 12 + (-5) = 7
- j = 3 → currentSum = 7 + (-6) = 1
- j = 4 → currentSum = 1 + 50 = 51
Sum of subarray [12, -5, -6, 50] = 51
Calculate average: currentAverage = 51 / 4 = 12.75
Update maxAverage: maxAverage = max(0.5, 12.75) = 12.75
Iteration i = 2
- Initialize currentSum = 0
Inner loop from j = 2 to j = 5
- j = 2 → currentSum = 0 + (-5) = -5
- j = 3 → currentSum = -5 + (-6) = -11
- j = 4 → currentSum = -11 + 50 = 39
- j = 5 → currentSum = 39 + 3 = 42
Sum of subarray [-5, -6, 50, 3] = 42
Calculate average: currentAverage = 42 / 4 = 10.5
Update maxAverage:maxAverage = max(12.75, 10.5) = 12.75
Step 2: Return the maximum average
After all iterations, maxAverage = 12.75
Return maxAverage = 12.75000 (formatted to 5 decimal places)
Final Output:
12.75000
Code for All Languages
C++
#include <iostream> // For input and output functions like cin and cout
#include <vector> // For using the vector data structure
using namespace std;
class Solution {
public:
double findMaxAverage(vector<int>& nums, int k) {
int n = nums.size();
// Step 1: Initialize the maximum average with a very small value
double maxAverage = -1e9;
// Step 2: Use a nested loop to check all subarrays of size k
for (int i = 0; i <= n - k; i++) {
double currentSum = 0;
// Sum the next 'k' elements starting from index i
for (int j = i; j < i + k; j++) {
currentSum += nums[j];
}
// Step 3: Calculate average of current window and update maxAverage if it's higher
double currentAverage = currentSum / k;
if (currentAverage > maxAverage) {
maxAverage = currentAverage;
}
}
// Step 4: Return the maximum average found
return maxAverage;
}
};
int main() {
int n, k;
// Input the size of the array and the window size k (no prompt as requested)
cin >> n >> k;
vector<int> nums(n);
// Input the elements of the array
for (int i = 0; i < n; i++) {
cin >> nums[i];
}
Solution sol;
// Call the function to find the maximum average subarray of size k
double result = sol.findMaxAverage(nums, k);
// Output the result with 5 digits precision as required
printf("%.5f\n", result);
return 0;
}Java
import java.util.Scanner; // For input
import java.util.Locale; // For setting locale to use dot as decimal separator
class Solution {
public double findMaxAverage(int[] nums, int k) {
int n = nums.length;
// Step 1: Initialize the maximum average with a very small value
double maxAverage = -1e9;
// Step 2: Use a nested loop to check all subarrays of size k
for (int i = 0; i <= n - k; i++) {
double currentSum = 0;
// Sum the next 'k' elements starting from index i
for (int j = i; j < i + k; j++) {
currentSum += nums[j];
}
// Step 3: Calculate average of current window and update maxAverage if it's higher
double currentAverage = currentSum / k;
if (currentAverage > maxAverage) {
maxAverage = currentAverage;
}
}
// Step 4: Return the maximum average found
return maxAverage;
}
}
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
sc.useLocale(Locale.US); // Ensure '.' is used as decimal separator
int n = sc.nextInt(); // Input the size of the array
int k = sc.nextInt(); // Input the window size
int[] nums = new int[n];
// Input the elements of the array
for (int i = 0; i < n; i++) {
nums[i] = sc.nextInt();
}
Solution sol = new Solution();
// Call the function to find the maximum average subarray of size k
double result = sol.findMaxAverage(nums, k);
// Output the result with 5 digits precision as required
System.out.printf("%.5f\n", result);
}
}
Python
from typing import List # For specifying the return type as a list of integers
class Solution:
def findMaxAverage(self, nums: List[int], k: int) -> float:
n = len(nums)
# Step 1: Initialize the maximum average with a very small value
max_average = -1e9
# Step 2: Use a nested loop to check all subarrays of size k
for i in range(n - k + 1):
current_sum = 0
# Sum the next 'k' elements starting from index i
for j in range(i, i + k):
current_sum += nums[j]
# Step 3: Calculate average of current window and update max_average if it's higher
current_average = current_sum / k
if current_average > max_average:
max_average = current_average
# Step 4: Return the maximum average found
return max_average
# Driver code
if __name__ == "__main__":
# Input the size of the array and the window size k (no prompt as requested)
n, k = map(int, input().split())
# Input the elements of the array
nums = list(map(int, input().split()))
sol = Solution()
# Call the function to find the maximum average subarray of size k
result = sol.findMaxAverage(nums, k)
# Output the result with 5 digits precision as required
print("{:.5f}".format(result))
Javascript
/**
* @param {number[]} nums - The input array of integers
* @param {number} k - The length of the subarray
* @return {number} - The maximum average of any subarray of length k
*/
var findMaxAverage = function(nums, k) {
const n = nums.length;
// Step 1: Initialize the maximum average with a very small value
let maxAverage = -1e9;
// Step 2: Use a nested loop to check all subarrays of size k
for (let i = 0; i <= n - k; i++) {
let currentSum = 0;
// Sum the next 'k' elements starting from index i
for (let j = i; j < i + k; j++) {
currentSum += nums[j];
}
// Step 3: Calculate average of current window and update maxAverage if it's higher
let currentAverage = currentSum / k;
if (currentAverage > maxAverage) {
maxAverage = currentAverage;
}
}
// Step 4: Return the maximum average found
return maxAverage;
};
// Example usage:
// Input reading (Node.js style - for online judges or terminals)
const readline = require('readline');
const rl = readline.createInterface({
input: process.stdin,
output: process.stdout
});
let inputLines = [];
rl.on('line', function(line) {
inputLines.push(line.trim());
if (inputLines.length === 2) {
rl.close();
}
});
rl.on('close', function() {
const [n, k] = inputLines[0].split(' ').map(Number);
const nums = inputLines[1].split(' ').map(Number);
const result = findMaxAverage(nums, k);
// Output the result with 5 digits precision as required
console.log(result.toFixed(5));
});Time Complexity: O(n * k)
Outer Loop: O(n - k + 1)
The outer loop runs from i = 0 to i <= n - k, where n is the length of the array and k is the window size.
So, the loop executes approximately (n - k + 1) times, which is O(n) in the worst case.
Inner Loop to Sum k Elements: O(k)
For each iteration of the outer loop, we run an inner loop from j = i to j < i + k.
This inner loop computes the sum of k elements of the current subarray.
Each access nums[j] is a constant-time operation, so this loop takes O(k) time per outer iteration.
Average Calculation and Max Update: O(1)
The division currentSum / k and comparison if (currentAverage > maxAverage) both take constant time.
So, this step takes O(1) time per outer iteration.
Total Time per Outer Loop Iteration: O(k)
Each iteration of the outer loop involves:
- Summing k elements → O(k)
- Calculating average and updating max → O(1)
Total work per iteration = O(k + 1) = O(k)
Final Time Complexity: O(n * k)
Since the outer loop runs O(n) times and each iteration takes O(k) time,
the total time complexity is O(n * k).
Where:
- n = number of elements in the array
- k = size of the subarray (window) to consider for average
Space Complexity: O(1)
Auxiliary Space Complexity: O(1)
This refers to any extra space used by the algorithm that is independent of the input and output space.
In this nested loop brute-force approach, we use only a few extra variables such as:
- maxAverage to store the maximum average found so far,
- currentSum and currentAverage to calculate sums and averages for each window.
No additional data structures or arrays proportional to the input size are used.
Therefore, the auxiliary space complexity is constant, i.e., O(1).
Total Space Complexity: O(n)
This includes:
- Input Space: The input array nums of size n occupies O(n) space.
- Auxiliary Space: As analyzed above, constant space O(1).
There is no extra output space required other than the returned value.
Combining these:
Total Space Complexity = O(n) + O(1) = O(n)
This makes the approach space-efficient, using only the space needed for the input and a fixed number of extra variables.
Why this Approach will give TLE?
The main reason this approach will give Time Limit Exceeded (TLE) is because of its high time complexity combined with large input sizes.
If the length of the array n is very large (for example, up to 10^5 or more), then:
- The outer loop runs approximately (n - k + 1) times, which is roughly O(n).
- For each iteration of the outer loop, the inner loop runs k times to calculate the sum of the current window.
This results in a total time complexity of approximately O(n * k).
If both n and k are large (e.g., n = 10^5 and k = 10^5), the total operations can reach up to 10^10, which is far beyond what can be executed within typical time limits (usually 1-3 seconds).
Competitive programming platforms expect solutions to run within around 10^7 to 10^8 operations per second.
Thus, the nested loop approach becomes too slow for large inputs and exceeds the allowed time, resulting in Time Limit Exceeded (TLE) errors.
We have seen the brute-force solution, which taught us how to check for subarrays using nested loops which can be quite expensive. Is it possible to eliminate the nested loops and improve the time complexity? Let’s find out as we move on to the optimal approach.
Optimal Approach
Intuition
Let’s take a moment to understand what this problem is really asking. We want to find a subarray of length k that has the highest average. A subarray means the elements must be contiguous — sitting next to each other in the array.
Now think about how we’d do this naively: check every subarray of length k, calculate its sum, divide by k, and track the maximum. But that gets inefficient as the array grows. Why? Because when we move from one subarray to the next, almost all the elements are the same — only one element leaves the window, and one new element enters. But brute-force ignores that and recalculates the whole sum from scratch. That’s what makes it inefficient: O(n * k) time in the worst case.
There has to be a better way, right?
That’s where the sliding window technique comes in — a super handy tool when dealing with problems like this. Instead of starting from scratch for every new subarray, we reuse the previous work.
What is Sliding Window Technique?
Imagine you’re looking at a long line of items — like numbers in an array or letters in a string — and you want to examine small parts (subarrays or substrings) of it one at a time.
The Sliding Window Technique helps us do this efficiently, without starting over every time.
Instead of recalculating everything from scratch for each part, we slide a “window” over the data, reusing most of the previous work.
What is a “Window”?
A window is just a small segment or a range within the array or string.
For example:
Let’s say we have this array: arr = [1, 2, 3, 4, 5, 6]
If we want to look at subarrays of size 3:
- First window: [1, 2, 3]
- Next window: [2, 3, 4]
- Then: [3, 4, 5], and so on...
Each time, we just move the window one step forward, dropping the first element and including the next.
Why Do We Use It?
Because it's efficient!
Let’s say we wanted the sum of each window of size 3:
Naive Way (Brute Force):
- For every window, loop through the 3 elements and sum them → O(n * k), where n = length of array, k = window size.
Sliding Window Way:
Sum the first window once. For the next window:
- Subtract the element going out of the window.
- Add the element coming in.
This makes each new window sum in O(1) time → total O(n).
Types of Sliding Windows
There are mainly two types:
1. Fixed-size Sliding Window - Window size stays the same.
2. Variable-size Sliding Window - The window grows or shrinks based on conditions.
In this problem, we are using fixed size Sliding Window as the window size if fixed, i.e. length of k.
We calculate the sum of the first k elements normally. Then, as we move the window forward:
- We subtract the element that’s leaving the window (on the left),
- And add the element that’s entering the window (on the right).
Just like that, we’ve updated the sum in O(1) time! No need to scan the entire k elements again.
Approach
Step 1: Initialize the First Window Sum
We prepare the initial state by calculating the sum of the first k elements of the array.
- We initialize a variable currentSum to 0.
- Using a loop from index 0 to k - 1, we add each element to currentSum.
This sum represents the total of the first sliding window and sets up our starting point for the algorithm.
Step 2: Set maxSum to the Initial Window Sum
We introduce a variable maxSum to track the highest sum encountered among all windows.
Initially, maxSum = currentSum, because the first window is the only one we've processed so far. This will later help us compare with future windows and update the maximum accordingly.
Step 3: Slide the Window Through the Array
We now process all other windows by sliding one element at a time from left to right. Loop from i = k to i < n. At each step:
- Subtract the element that is leaving the window: nums[i - k]
- Add the new element that is entering the window: nums[i]
- Update currentSum with this new value
- If currentSum is greater than maxSum, update maxSum
This efficient window update ensures we are not recalculating the entire window sum repeatedly.
Step 4: Return the Maximum Average
Once the window has moved through the entire array. Divide maxSum by k to get the maximum average value. Return this value as the final result.

Dry Run
Let’s do a step-by-step dry run of the optimized sliding window approach for the input:
nums = [1, 12, -5, -6, 50, 3], k = 4
We aim to find the maximum average of any subarray of size 4.
Step 1: Initialize the First Window Sum
We compute the sum of the first k = 4 elements of the array:
- currentSum = 1 + 12 + (-5) + (-6) = 2
We also set:
- maxSum = currentSum = 2
So the first window is [1, 12, -5, -6] with sum = 2 and average = 0.5
Step 2: Slide the Window Across the Array
We begin sliding the window one element at a time starting from index k = 4 up to n - 1 = 5
i = 4
- Element going out of the window: nums[4 - 4] = nums[0] = 1
- Element coming into the window: nums[4] = 50
Update currentSum:
- currentSum = 2 - 1 + 50 = 51
Update maxSum:
- maxSum = max(2, 51) = 51
Current window: [12, -5, -6, 50]
Window sum: 51
Window average: 51 / 4 = 12.75 → so far this is the maximum
i = 5
- Element going out of the window: nums[5 - 4] = nums[1] = 12
- Element coming into the window: nums[5] = 3
Update currentSum:
- currentSum = 51 - 12 + 3 = 42
Update maxSum:
- maxSum = max(51, 42) = 51
Current window: [-5, -6, 50, 3]
Window sum: 42
Window average: 42 / 4 = 10.5 → not greater than current max
Step 3: Return the Maximum Average
After the loop, the final value of maxSum = 51
We return:
- maxSum / k = 51 / 4 = 12.75000
This is the maximum average of all subarrays of size 4.
Final Output:
12.75000
Code for All Languages
C++
#include <iostream> // For input and output functions like cin and cout
#include <vector> // For using the vector data structure
using namespace std;
class Solution {
public:
double findMaxAverage(vector<int>& nums, int k) {
int n = nums.size();
// Step 1: Compute the sum of the first 'k' elements to initialize the sliding window
double currentSum = 0;
for (int i = 0; i < k; i++) {
currentSum += nums[i];
}
// Step 2: Initialize maxSum with the sum of the first window
double maxSum = currentSum;
// Step 3: Slide the window across the array from index k to n-1
for (int i = k; i < n; i++) {
// Subtract the element that’s sliding out and add the new element coming into the window
currentSum = currentSum - nums[i - k] + nums[i];
// Update maxSum if current window sum is greater
if (currentSum > maxSum) {
maxSum = currentSum;
}
}
// Step 4: Return the maximum average found (maxSum divided by window size k)
return maxSum / k;
}
};
int main() {
int n, k;
// Input the size of the array and the window size k (no prompt as requested)
cin >> n >> k;
vector<int> nums(n);
// Input the elements of the array
for (int i = 0; i < n; i++) {
cin >> nums[i];
}
Solution sol;
// Call the function to find the maximum average subarray of size k
double result = sol.findMaxAverage(nums, k);
// Output the result with 5 digits precision as required
printf("%.5f\n", result);
return 0;
}Java
import java.util.Scanner; // For input
import java.util.Locale; // For setting locale to use dot as decimal separator
class Solution {
public double findMaxAverage(int[] nums, int k) {
int n = nums.length;
// Step 1: Compute the sum of the first 'k' elements to initialize the sliding window
double currentSum = 0;
for (int i = 0; i < k; i++) {
currentSum += nums[i];
}
// Step 2: Initialize maxSum with the sum of the first window
double maxSum = currentSum;
// Step 3: Slide the window across the array from index k to n-1
for (int i = k; i < n; i++) {
// Subtract the element that’s sliding out and add the new element coming into the window
currentSum = currentSum - nums[i - k] + nums[i];
// Update maxSum if current window sum is greater
if (currentSum > maxSum) {
maxSum = currentSum;
}
}
// Step 4: Return the maximum average found (maxSum divided by window size k)
return maxSum / k;
}
}
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
sc.useLocale(Locale.US); // Ensure '.' is used as decimal separator
int n = sc.nextInt(); // Input the size of the array
int k = sc.nextInt(); // Input the window size
int[] nums = new int[n];
// Input the elements of the array
for (int i = 0; i < n; i++) {
nums[i] = sc.nextInt();
}
Solution sol = new Solution();
// Call the function to find the maximum average subarray of size k
double result = sol.findMaxAverage(nums, k);
// Output the result with 5 digits precision as required
System.out.printf("%.5f\n", result);
}
}
Python
from typing import List
class Solution:
def findMaxAverage(self, nums: List[int], k: int) -> float:
n = len(nums)
# Step 1: Compute the sum of the first 'k' elements to initialize the sliding window
current_sum = sum(nums[:k])
# Step 2: Initialize max_sum with the sum of the first window
max_sum = current_sum
# Step 3: Slide the window across the array from index k to n-1
for i in range(k, n):
# Subtract the element that’s sliding out and add the new element coming into the window
current_sum = current_sum - nums[i - k] + nums[i]
# Update max_sum if current window sum is greater
if current_sum > max_sum:
max_sum = current_sum
# Step 4: Return the maximum average found (max_sum divided by window size k)
return max_sum / k
if __name__ == "__main__":
# Input the size of the array and the window size k (no prompt as requested)
n, k = map(int, input().split())
# Input the elements of the array
nums = list(map(int, input().split()))
sol = Solution()
# Call the function to find the maximum average subarray of size k
result = sol.findMaxAverage(nums, k)
# Output the result with 5 digits precision as required
print(f"{result:.5f}")
Javascript
/**
* @param {number[]} nums - The input array of integers
* @param {number} k - The length of the subarray
* @return {number} - The maximum average of any subarray of length k
*/
var findMaxAverage = function(nums, k) {
const n = nums.length;
// Step 1: Compute the sum of the first 'k' elements to initialize the sliding window
let currentSum = 0;
for (let i = 0; i < k; i++) {
currentSum += nums[i];
}
// Step 2: Initialize maxSum with the sum of the first window
let maxSum = currentSum;
// Step 3: Slide the window across the array from index k to n-1
for (let i = k; i < n; i++) {
// Subtract the element that’s sliding out and add the new element coming into the window
currentSum = currentSum - nums[i - k] + nums[i];
// Update maxSum if current window sum is greater
if (currentSum > maxSum) {
maxSum = currentSum;
}
}
// Step 4: Return the maximum average found (maxSum divided by window size k)
return maxSum / k;
};
// Example usage:
// Input reading (Node.js style - for online judges or terminals)
const readline = require('readline');
const rl = readline.createInterface({
input: process.stdin,
output: process.stdout
});
let inputLines = [];
rl.on('line', function(line) {
inputLines.push(line.trim());
if (inputLines.length === 2) {
rl.close();
}
});
rl.on('close', function() {
const [n, k] = inputLines[0].split(' ').map(Number);
const nums = inputLines[1].split(' ').map(Number);
const result = findMaxAverage(nums, k);
// Output the result with 5 digits precision as required
console.log(result.toFixed(5));
});Time Complexity: O(n)
Let:
- n = length of the input array nums
- k = size of the sliding window
Initial Window Sum Calculation – O(k)
We compute the sum of the first k elements using a loop from index 0 to k - 1.
This loop runs exactly k times.
So, this step takes O(k) time.
Sliding Window Loop – O(n - k)
We slide the window from index k to n - 1.
At each step:
- Subtract the element going out of the window: nums[i - k]
- Add the element coming into the window: nums[i]
- Compare/update the maxSum if needed
Each operation (subtraction, addition, comparison) takes constant time O(1). The loop runs for (n - k) iterations. Hence, this step takes O(n - k) time.
Final Division – O(1)
After computing the maximum sum, we return the average by dividing by k.
This is a single arithmetic operation and takes O(1) time.
Final Time Complexity: O(n)
- Initial sum calculation: O(k)
- Sliding window updates: O(n - k)
- Total: O(k + n - k) = O(n)
So, the overall time complexity is O(n), where n is the number of elements in the array.
Space Complexity: O(1)
Auxiliary Space Complexity: O(1)
This refers to any extra space used by the algorithm that is independent of the input and output sizes.
In this sliding window approach, we only use a few variables:
- currentSum: to store the sum of the current window
- maxSum: to keep track of the maximum window sum
- n: to store the size of the array
These are all scalar variables (not data structures), and they take constant space regardless of the input size.
Thus, the auxiliary space complexity is O(1).
Total Space Complexity: O(n)
This includes:
Input Space:
- The input vector nums contains n integers. So, the input space is O(n).
Output Space:
- The output is a single floating-point number representing the maximum average. Since this is a single value, it takes O(1) space.
Auxiliary Space:
- As analyzed above, it is O(1).
Total Space Complexity = O(n) + O(1) + O(1) = O(n)
Learning Tip
Now we have successfully tackled this problem, let's try these similar problems.
Given two strings s1 and s2, return true if s2 contains a permutation of s1, or false otherwise.
In other words, return true if one of s1's permutations is the substring of s2.
Given a string s and an integer k, return the maximum number of vowel letters in any substring of s with length k. Vowel letters in English are 'a', 'e', 'i', 'o', and 'u'.