Longest Subarray of 1's After Deleting One Element Solution In C++/Java/Python/JS
Problem Description
Given a binary array nums, you should delete one element from it.
Return the size of the longest non-empty subarray containing only 1's in the resulting array. Return 0 if there is no such subarray.
Example
Example 1:
Input: nums = [1,1,0,1]
Output: 3
Explanation: After deleting the number in position 2, [1,1,1] contains 3 numbers with value of 1's.
Example 2:
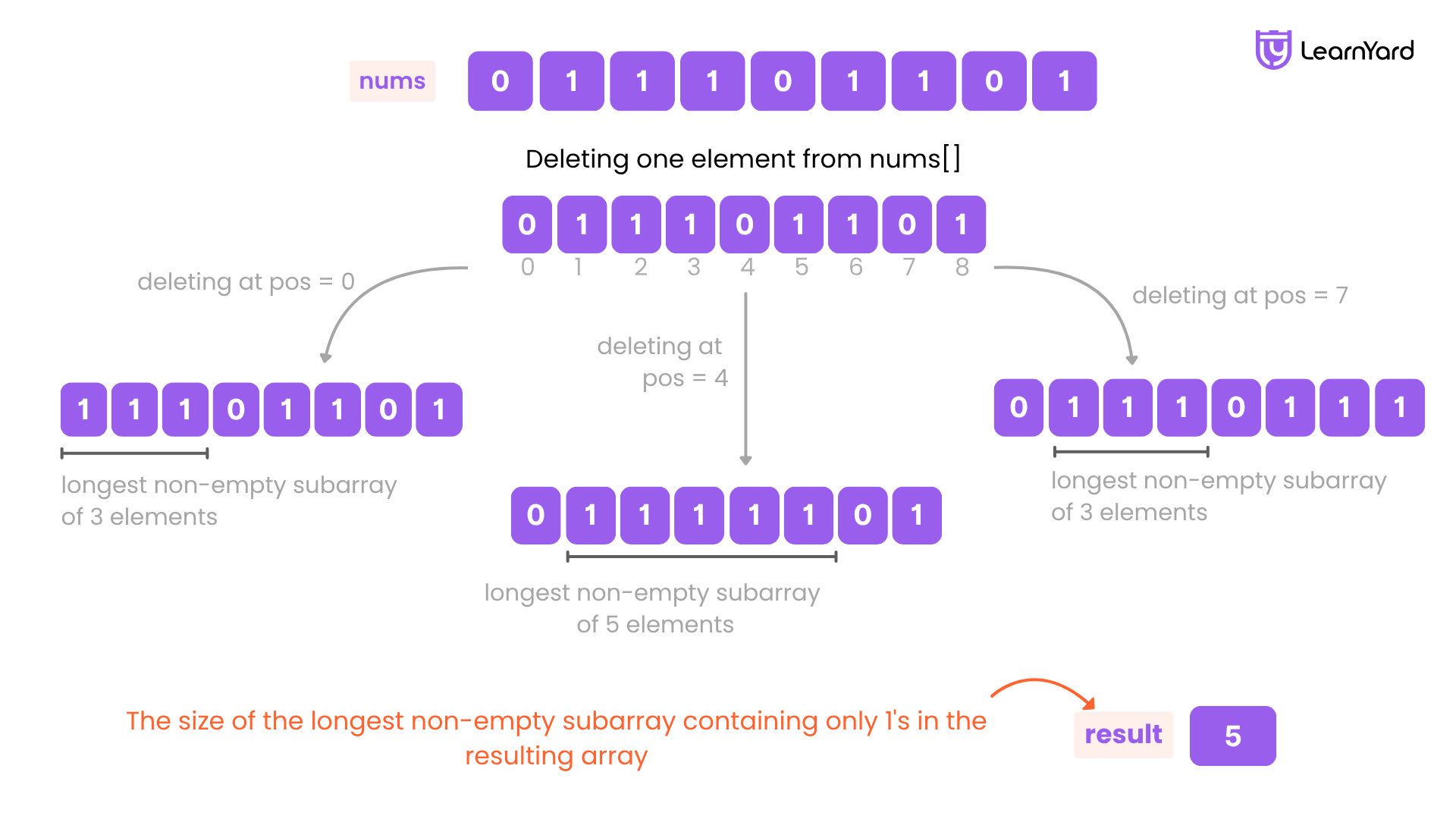
Input: nums = [0,1,1,1,0,1,1,0,1]
Output: 5
Explanation: After deleting the number in position 4, [0,1,1,1,1,1,0,1] longest subarray with value of 1's is [1,1,1,1,1].
Example 3:
Input: nums = [1,1,1]
Output: 2
Explanation: You must delete one element.
Constraints
- 1 <= nums.length <= 10^5
- nums[i] is either 0 or 1.
Let's tackle the problem “Longest Subarray of 1's After Deleting One Element” step by step. We'll start by understanding the most intuitive solution and then work our way toward a more optimized approach, if one exists. So, grab a pen and paper, and let's break down the algorithm together!
Brute Force Approach
Intuition
If we break down this problem, we are given a binary array nums consisting of only 0s and 1s. The task is to delete exactly one element and then find the length of the longest contiguous subarray that contains only 1s.
Now, if we observe carefully, we realize that the challenge is to find the longest stretch of 1s after deleting a single element, which could be either:
- A 0 that is breaking a sequence of 1s, or
- A 1, in case the array has all 1s (we’re forced to delete one).
So, the first idea that comes to our mind is:
Why don't we try deleting every 0 from the array and check the longest sequence of 1's results from that?
This makes sense because:
- Deleting a 0 can merge two sequences of 1's on either side of it.
- This might give us a longer contiguous subarray of 1's.
Let’s illustrate this with an example:
nums = [1, 1, 0, 1, 1]
If we delete the 0 at index 2 We get:
[1, 1, 1, 1] → length = 4
Clearly, deleting a 0 connects the left and right 1s and increases the length of the 1's streak.
So if we do the same for every 0 in the array and finds the longest Sequence from them then result will be longest Sequence of 1's in array.
But there is one important edge case we must handle:
What if the array contains all 1's and no 0s at all?
Example:
nums = [1, 1, 1, 1, 1]
In this case:
- There is no 0 to delete.
- But the problem says we must delete exactly one element.
- So we have no choice but to delete a 1.
Resulting array:
[1, 1, 1, 1] → length = 4
Therefore:
- If the array contains only 1's, we should return n - 1 where n is the length of the array.
This ensures that we still follow the rule of deleting exactly one element.
Longest Subarray of 1's After Deleting One Element Algorithm
Step 1: Initialize Variables
- Create an integer ans = 0 to store the final result.
- Create a boolean flag check = true to check if all elements are 1.
Step 2: Check if All Elements are 1
- Loop through the array nums[]:
- If any element is 0, set check = false and break the loop.
- If check is still true:
- Return nums.length - 1 (since we must delete one element).
Step 3: Try Deleting Every 0 in the Array
- Loop through each index i from 0 to nums.length - 1:
- If nums[i] == 0, simulate deleting this element:
- Initialize curr = 0 to count current sequence of 1's.
- Loop through each index j from 0 to nums.length - 1:
- If j == i, continue (skip the deleted element).
- If nums[j] == 1, increment curr.
- Update ans = max(ans, curr).
- Else (nums[j] == 0), reset curr = 0.
- If nums[i] == 0, simulate deleting this element:
Step 4: Return the Result
- After all possible deletions are tested, return ans.
Dry-Run
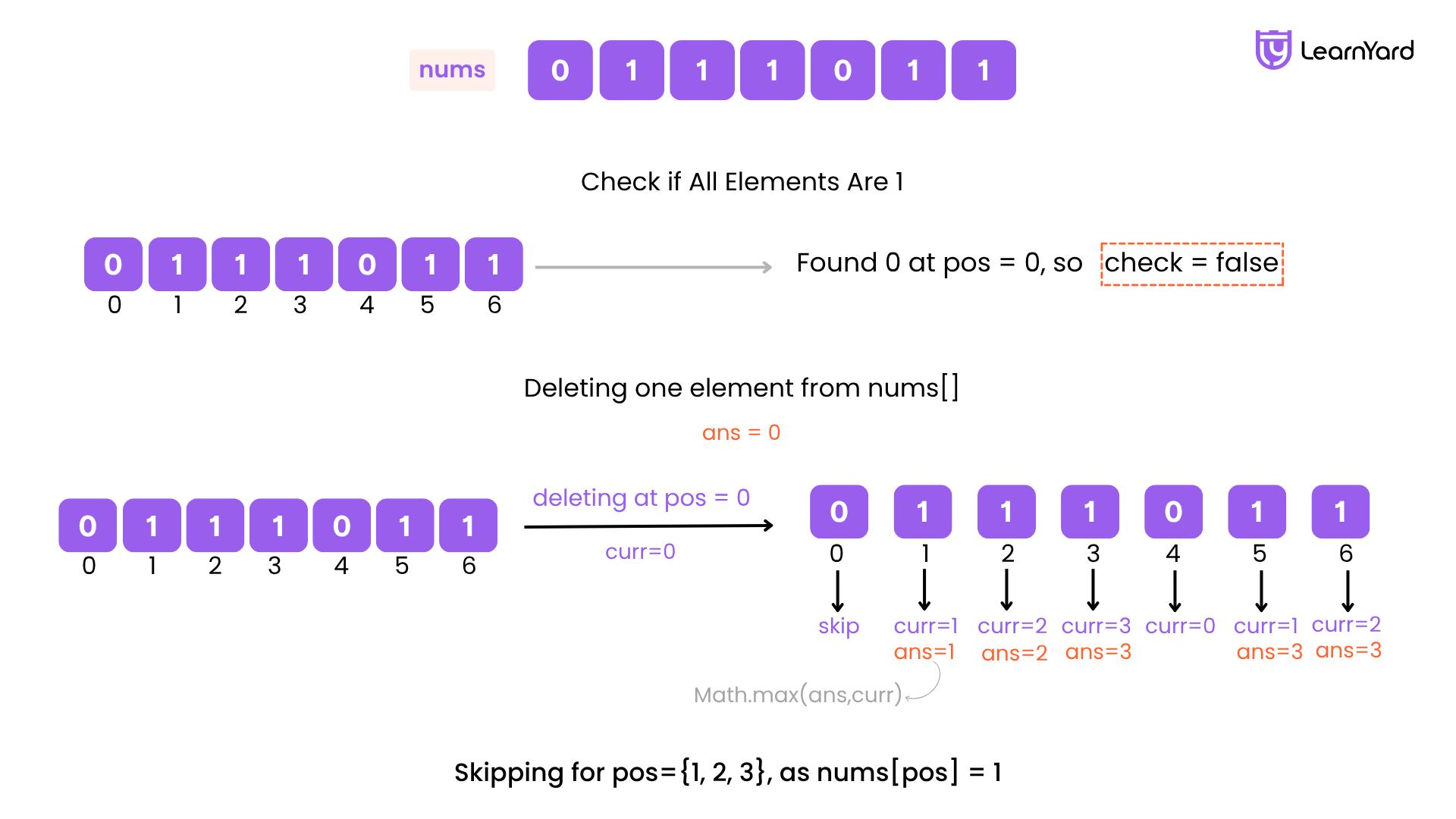
Input: nums = [1, 1, 0, 1, 1]
Step 1: Initialize Variables:
ans = 0
check = true
Step 2: Check if All Elements Are 1
Loop through each element:
- nums[0] = 1 → check = true
- nums[1] = 1 → check = true
- nums[2] = 0 → check = false → break the loop
So, not all elements are 1 → we do not return early
Step 3: Try Deleting Every 0 in the Array
Loop i from 0 to nums.length - 1:
First Iteration (i = 0)
nums[0] = 1 → skip (we only delete 0s)
Second Iteration (i = 1)
nums[1] = 1 → skip
Third Iteration (i = 2)
nums[2] = 0 → simulate deletion at index 2
curr = 0
Loop j = 0 to 4:
- j = 0: j ≠ i, nums[0] = 1 → curr = 1 → ans = max(0, 1) = 1
- j = 1: j ≠ i, nums[1] = 1 → curr = 2 → ans = max(1, 2) = 2
- j = 2: j == i → skip
- j = 3: j ≠ i, nums[3] = 1 → curr = 3 → ans = max(2, 3) = 3
- j = 4: j ≠ i, nums[4] = 1 → curr = 4 → ans = max(3, 4) = 4
Result after deleting nums[2]: curr = 4, ans = 4
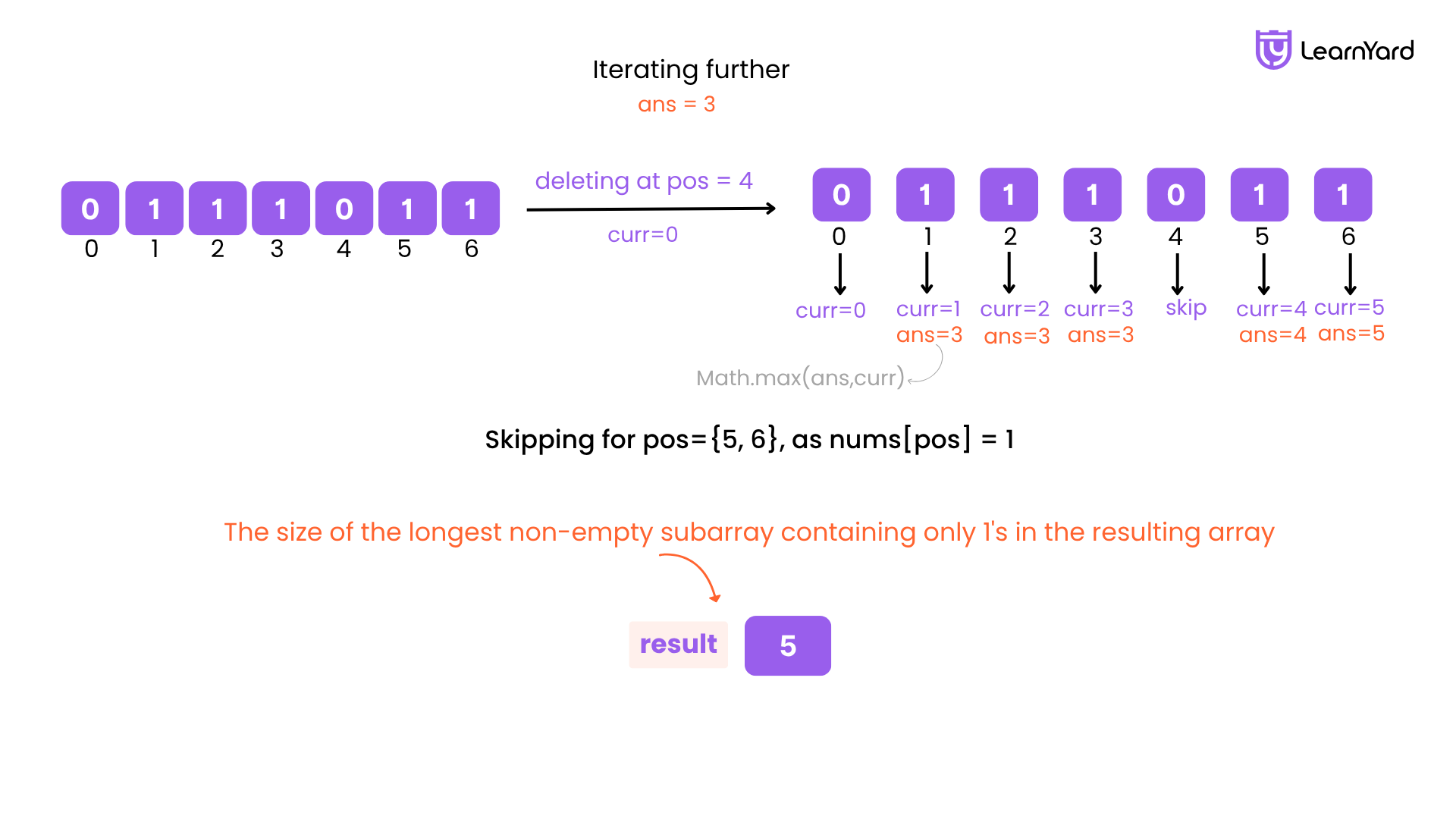
Fourth Iteration (i = 3)
nums[3] = 1 → skip
Fifth Iteration (i = 4)
nums[4] = 1 → skip
Final Step: Return the Result:
Return ans = 4
Longest Subarray of 1's After Deleting One Element Solution
Now let's check out the Longest Subarray of 1's After Deleting One Element code in C++ , Java, Python and JavaScript.
"Longest Subarray of 1's After Deleting One Element" Code in all Languages.
1. Longest Subarray of 1's After Deleting One Element solution in C++ Try on Compiler
#include <iostream>
#include <vector>
using namespace std;
class Solution {
public:
int longestSubarray(vector<int>& nums) {
int ans = 0;
bool check = true;
for (int i = 0; i < nums.size(); i++) {
if (nums[i] == 0) {
check = false;
break;
}
}
if (check) return nums.size() - 1;
for (int i = 0; i < nums.size(); i++) {
if (nums[i] == 0) {
int curr = 0;
for (int j = 0; j < nums.size(); j++) {
if (i == j) continue;
if (nums[j] == 1) {
curr++;
ans = max(ans, curr);
} else {
curr = 0;
}
}
}
}
return ans;
}
};
int main() {
int n;
cin >> n;
vector<int> nums(n);
for (int i = 0; i < n; i++) cin >> nums[i];
Solution sol;
cout << sol.longestSubarray(nums) << endl;
}
2. Longest Subarray of 1's After Deleting One Element Solution in Java Try on Compiler
import java.util.*;
public class Main {
public static int longestSubarray(int[] nums) {
int ans = 0;
boolean check = true;
for (int i = 0; i < nums.length; i++) {
if (nums[i] == 0) {
check = false;
break;
}
}
if (check) return nums.length - 1;
for (int i = 0; i < nums.length; i++) {
if (nums[i] == 0) {
int curr = 0;
for (int j = 0; j < nums.length; j++) {
if (i == j) continue;
if (nums[j] == 1) {
curr++;
ans = Math.max(ans, curr);
} else {
curr = 0;
}
}
}
}
return ans;
}
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
int[] nums = new int[n];
for (int i = 0; i < n; i++) {
nums[i] = sc.nextInt();
}
System.out.println(longestSubarray(nums));
}
}
3. Longest Subarray of 1's After Deleting One Element Solution in Python Try on Compiler
class Solution:
def longestSubarray(self, nums):
ans = 0
check = True
for num in nums:
if num == 0:
check = False
break
if check:
return len(nums) - 1
for i in range(len(nums)):
if nums[i] == 0:
curr = 0
for j in range(len(nums)):
if j == i:
continue
if nums[j] == 1:
curr += 1
ans = max(ans, curr)
else:
curr = 0
return ans
n = int(input())
nums = list(map(int, input().split()))
print(Solution().longestSubarray(nums))
4. Longest Subarray of 1's After Deleting One Element solution in JavaScript Try on Compiler
class Solution {
longestSubarray(nums) {
let ans = 0;
let check = true;
for (let i = 0; i < nums.length; i++) {
if (nums[i] === 0) {
check = false;
break;
}
}
if (check) return nums.length - 1;
for (let i = 0; i < nums.length; i++) {
if (nums[i] === 0) {
let curr = 0;
for (let j = 0; j < nums.length; j++) {
if (j === i) continue;
if (nums[j] === 1) {
curr++;
ans = Math.max(ans, curr);
} else {
curr = 0;
}
}
}
}
return ans;
}
}
const readline = require("readline");
const rl = readline.createInterface({
input: process.stdin,
output: process.stdout
});
let input = [];
rl.on("line", function (line) {
input.push(line.trim());
if (input.length === 2) {
const n = parseInt(input[0]);
const nums = input[1].split(" ").map(Number);
const sol = new Solution();
console.log(sol.longestSubarray(nums));
rl.close();
}
});
Longest Subarray of 1's After Deleting One Element: Complexity Analysis
Time Complexity: O(n^2)
Initial Check Loop: O(n)
The loop runs from index i = 0 to i = n - 1, scanning all elements to check if all are 1s.
Let’s denote:
- n = number of elements in the input array
So, the loop executes n times, which is O(n).
Outer Loop (for each 0): O(n)
This loop iterates through the entire array once to identify indices with value 0.
So, the outer loop runs at most n times → O(n)
Inner Loop (skipping one element): O(n)
For each 0 found at index i, the inner loop runs from j = 0 to j = n - 1, skipping index i.
Each such inner loop takes O(n) time.
Total Work Done: O(n^2)
In the worst case, if the array has multiple zeros, the outer loop could run multiple times and each time invoke an inner loop of size n.
Thus, total time = O(n) * O(n) = O(n²)
Input Reading Loop: O(n)
Reading n elements from input takes O(n) time.
Final Time Complexity: O(n²)
We perform O(n) operations multiple times in the worst case, leading to total time complexity of O(n²)
Where:
- n is the number of elements in the input array.
Space Complexity: O(1)
Auxiliary Space Complexity: O(1)
This refers to any extra space used by the algorithm that is independent of the input and output space.
In this approach, we use:
- A few integer variables (ans, curr, i, j)
- A boolean flag (check)
All of these take constant space → O(1)
Total Space Complexity: O(n)
This includes the space required for:
- Input space: The input array of length n → O(n)
- Output space: A single integer is returned → O(1)
- Extra space used by the algorithm: As analyzed above → O(1)
Combining all the space requirements:
Total Space Complexity = O(n) + O(1) + O(1) = O(n)
Where:
- n is the number of elements in the input array.
Optimal Approach
Intuition
In brute force approach, we try deleting each 0 in the array one by one and then count the length of the longest contiguous subarray consisting only of 1s after that deletion. This involves nested loops and leads to a time complexity of O(n²), which becomes inefficient for large arrays. So, what are we doing with brute force? We're trying to find the longest sequence of consecutive 1s that we can get after removing one element, usually a 0. That naturally leads to the question: instead of deleting each 0 one by one, can we somehow keep track of a range in the array where we allow just one 0?
That’s exactly the kind of condition where a sliding window can help. What if instead of manually deleting every 0, we maintain a window that contains at most one 0 at any time?
Using two pointers, we can dynamically maintain a window that contains at most one 0 and slide the window across the array in a single pass. Whenever we encounter more than one 0, we shrink the window from the left until the condition is satisfied again. Throughout this process, we track the maximum valid window size. Since the problem requires deleting exactly one element, we subtract 1 from the final window length. This will be our final answer. This makes our time complexity to O(n) that is much efficient.
Longest Subarray of 1's After Deleting One Element Algorithm
Step 1: Initialize Pointers and Variables
- Set two pointers: left = 0 and right = 0
- Initialize zeroCount = 0 → to count the number of 0's in the current window
- Initialize maxLen = 0 → to store the maximum window length
Step 2: Traverse the Array Using Right Pointer
While right < n:
- If nums[right] == 0, increment zeroCount
- While zeroCount > 1:
- If nums[left] == 0, decrement zeroCount
- Move left pointer forward (left++)
- Update maxLen = max(maxLen, right - left)
- Move right++
Step 3: Return Final Answer
- Since we must delete one element, return maxLen (already adjusted by right - left)
Let us understand this with a video,
Dry-Run
Input:
nums = [1, 1, 0, 1, 1]
Step 1: Initialize Variables
left = 0
right = 0
zeroCount = 0
maxLen = 0
Step 2: Traverse the Array Using Sliding Window
First Iteration (right = 0)
- nums[0] = 1 → zeroCount remains 0
- zeroCount ≤ 1 → valid window
- maxLen = max(0, 0 - 0) = 0
- right++ → right = 1
Second Iteration (right = 1)
- nums[1] = 1 → zeroCount remains 0
- zeroCount ≤ 1 → valid window
- maxLen = max(0, 1 - 0) = 1
- right++ → right = 2
Third Iteration (right = 2)
- nums[2] = 0 → zeroCount = 1
- zeroCount ≤ 1 → valid window
- maxLen = max(1, 2 - 0) = 2
- right++ → right = 3
Fourth Iteration (right = 3)
- nums[3] = 1 → zeroCount = 1
- zeroCount ≤ 1 → valid window
- maxLen = max(2, 3 - 0) = 3
- right++ → right = 4
Fifth Iteration (right = 4)
- nums[4] = 1 → zeroCount = 1
- zeroCount ≤ 1 → valid window
- maxLen = max(3, 4 - 0) = 4
- right++ → right = 5
Step 3: End of Array Reached
- Final right = 5 → loop ends
Step 4: Return the Result
Return maxLen = 4
Longest Subarray of 1's After Deleting One Element Solution
Now let's check out the Longest Subarray of 1's After Deleting One Element code in C++ , Java, Python and JavaScript.
"Longest Subarray of 1's After Deleting One Element" Code in all Languages.
1. Longest Subarray of 1's After Deleting One Element solution in C++ Try on Compiler
#include <iostream>
#include <vector>
using namespace std;
class Solution {
public:
int longestSubarray(vector<int>& nums) {
int left = 0; // Left pointer of the window
int zeroCount = 0; // Count of zeros in the current window
int maxLen = 0; // Maximum length found
for (int right = 0; right < nums.size(); right++) {
if (nums[right] == 0) {
zeroCount++; // Count the zero
}
while (zeroCount > 1) {
if (nums[left] == 0) {
zeroCount--; // Shrink window to remove extra zero
}
left++; // Move left pointer forward
}
maxLen = max(maxLen, right - left); // Update maximum length
}
return maxLen;
}
};
int main() {
int n;
cin >> n; // Input size
vector<int> nums(n);
for (int i = 0; i < n; i++) {
cin >> nums[i]; // Input array elements
}
Solution sol;
cout << sol.longestSubarray(nums) << endl; // Print result
}
2. Longest Subarray of 1's After Deleting One Element Solution in Java Try on Compiler
import java.util.*;
class Main {
public static int longestSubarray(int[] nums) {
int left = 0; // Left pointer of window
int zeroCount = 0; // Count of zeros in the window
int maxLen = 0; // Maximum length found
for (int right = 0; right < nums.length; right++) {
if (nums[right] == 0) {
zeroCount++; // Count the zero
}
while (zeroCount > 1) {
if (nums[left] == 0) {
zeroCount--; // Shrink window from left
}
left++;
}
maxLen = Math.max(maxLen, right - left); // Update max length
}
return maxLen;
}
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt(); // Input size
int[] nums = new int[n];
for (int i = 0; i < n; i++) {
nums[i] = sc.nextInt(); // Input array elements
}
System.out.println(longestSubarray(nums)); // Print result
}
}
3. Longest Subarray of 1's After Deleting One Element Solution in Python Try on Compiler
class Solution:
def longestSubarray(self, nums):
left = 0 # Left pointer of the window
zero_count = 0 # Count of zeros in the window
max_len = 0 # Maximum length found
for right in range(len(nums)):
if nums[right] == 0:
zero_count += 1 # Count the zero
while zero_count > 1:
if nums[left] == 0:
zero_count -= 1 # Shrink window
left += 1
max_len = max(max_len, right - left) # Update maximum
return max_len
n = int(input()) # Input size
nums = list(map(int, input().split())) # Input array elements
print(Solution().longestSubarray(nums)) # Print result
4. Longest Subarray of 1's After Deleting One Element solution in JavaScript Try on Compiler
class Solution {
longestSubarray(nums) {
let left = 0; // Left pointer
let zeroCount = 0; // Count of zeros in the window
let maxLen = 0; // Maximum length found
for (let right = 0; right < nums.length; right++) {
if (nums[right] === 0) {
zeroCount++; // Count zero
}
while (zeroCount > 1) {
if (nums[left] === 0) {
zeroCount--; // Shrink window
}
left++;
}
maxLen = Math.max(maxLen, right - left); // Update max length
}
return maxLen;
}
}
const readline = require("readline");
const rl = readline.createInterface({
input: process.stdin,
output: process.stdout
});
let input = [];
rl.on("line", function (line) {
input.push(line.trim());
if (input.length === 2) {
const n = parseInt(input[0]); // Input size
const nums = input[1].split(" ").map(Number); // Input array
const sol = new Solution();
console.log(sol.longestSubarray(nums)); // Print result
rl.close();
}
});
Longest Subarray of 1's After Deleting One Element Complexity Analysis
Time Complexity: O(n)
Outer Loop: O(n)
The loop runs from right = 0 to right = n - 1.
Let’s denote:
- n = number of elements in the input array
So, the outer loop executes n times, which is O(n).
Inner While Loop: O(n)
The inner while (zeroCount > 1) loop shrinks the window from the left.
Although it’s nested, the left pointer only moves forward and never backtracks.
Over the entire algorithm, both right and left traverse the array at most once.
Therefore, the total number of operations in both loops combined is linear — O(n).
Input Reading Loop: O(n)
Reading n elements from input takes O(n) time.
Final Time Complexity: O(n)
We perform O(1) operations for each element, and each pointer (left and right) moves across the array once.
So, the total time complexity is: O(n)
Where:
- n is the number of elements in the input array.
Space Complexity: O(1)
Auxiliary Space Complexity: O(1)
This refers to any extra space used by the algorithm that is independent of the input and output space.
In this approach, we use:
- Integer variables: left, right, zeroCount, maxLen
All of these take constant space → O(1)
Total Space Complexity: O(n)
This includes the space required for:
- Input space: The input array of length
n→ O(n) - Output space: A single integer is returned → O(1)
- Extra space used by the algorithm: As analyzed above → O(1)
Combining all the space requirements:
Total Space Complexity = O(n) + O(1) + O(1) = O(n)
Where:
- n is the number of elements in the input array.
Similar Problems
Given a binary array nums and an integer k, return the maximum number of consecutive 1's in the array if you can flip at most k 0's.