Largest Merge Of Two Strings Solution In C++/Java/Python/JS
Problem Description
You are given two strings word1 and word2. You want to construct a string merge in the following way: while either word1 or word2 are non-empty, choose one of the following options:
If word1 is non-empty, append the first character in word1 to merge and delete it from word1.
For example, if word1 = "abc" and merge = "dv", then after choosing this operation, word1 = "bc" and merge = "dva".
If word2 is non-empty, append the first character in word2 to merge and delete it from word2.
For example, if word2 = "abc" and merge = "", then after choosing this operation, word2 = "bc" and merge = "a".
Return the lexicographically largest merge you can construct.
A string a is lexicographically larger than a string b (of the same length) if in the first position where a and b differ, a has a character strictly larger than the corresponding character in b. For example, "abcd" is lexicographically larger than "abcc" because the first position they differ is at the fourth character, and d is greater than c.

Example
Input: word1 = "cabaa", word2 = "bcaaa"
Output: "cbcabaaaaa"
Explanation: One way to get the lexicographically largest merge is:
- Take from word1: merge = "c", word1 = "abaa", word2 = "bcaaa"
- Take from word2: merge = "cb", word1 = "abaa", word2 = "caaa"
- Take from word2: merge = "cbc", word1 = "abaa", word2 = "aaa"
- Take from word1: merge = "cbca", word1 = "baa", word2 = "aaa"
- Take from word1: merge = "cbcab", word1 = "aa", word2 = "aaa"
- Append the remaining 5 a's from word1 and word2 at the end of merge.
Input: word1 = "abcabc", word2 = "abdcaba"
Output: abdcabcabcaba
Explanation: Compare prefixes and pick from word2: "a", "b", "d" → merge = "abd".
- word2 = "caba" > word1 = "abcabc", so take "c" from word2 → merge = "abdc"
- Now word1 > word2, take "a", "b", "c" from word1 → merge = "abdcabc"
- word1 > word2, continue taking from word1 → "a", "b", "c"
- Append leftover "aba" from word2 → final merge = "abdcabcabcaba"
Constraints
- 1 <= word1.length, word2.length <= 3000
- word1 and word2 consist only of lowercase English letters.
Figuring out "Largest Merge Of Two Strings" can be solved using different approaches. We will first figure out the most intuitive approach and move to the optimal approach if exists. Let's sit with a pen and paper and figure out the algorithm !!
Optimal Approach
Intuition
We’re given two strings — we’ll call them word1 and word2. We can create a merged string by taking characters one-by-one from either word1 or word2, but only from the front of each. Think of it like peeling letters off the left side and attaching them to a new result string.
The challenge? We can only take one character at a time, from the start of either string, and we want the final merged string to be lexicographically the largest possible.
So how do we do that?
Maybe you're thinking: just compare the first characters of word1 and word2 at each step, and always take the larger one, right? That feels natural — it's the greedy thing to do.
What Does “Lexicographically Largest” Mean?
When we say a string is lexicographically larger, we’re talking about the same way words are sorted in a dictionary. You go letter by letter, left to right, and compare. The first difference you find decides which word comes first.
Here’s how it works:
- 'z' > 'a' — because 'z' comes after 'a'
- 'dog' < 'zebra' — because 'd' comes before 'z'
- 'abc' < 'abcd' — because 'abc' ends earlier, and a shorter word is smaller if all letters match
- 'bed' > 'be' — even though both start with 'b' and 'e', 'd' > nothing, so 'bed' wins
A good mental trick:
Think of comparing strings like this — you’re lining them up and reading left to right, and the first place they differ? That’s the tie-breaker.
So, when we say we want the lexicographically largest string, we mean:
The one that would appear last if we listed all the possible options in dictionary order.
Basically:
Later = greater.
The further down in the dictionary, the better.
Let’s Try It: One Letter at a Time
Let’s walk through an example and see what happens when we stick with the most obvious approach — comparing just one character from each string at a time. No fancy strategies yet. Just look at the first character of word1 and the first of word2, and pick whichever is bigger.
We’ll use these two strings:
- word1 = "ebdbba"
- word2 = "debbbd"
Our goal is to merge them into one string — by always taking a letter from the front of either string — and end up with the best, most lexicographically “last” result we can. So let’s start merging:
The first letters are 'e' and 'd'. Easy — 'e' is bigger. So we take that from word1. Now we have:
- merged = "e"
- word1 = "bdbba", word2 = "debbbd"
Now it's 'b' vs 'd'. 'd' wins, so we pull that from word2:
- merged = "ed"
- word1 = "bdbba", word2 = "ebbbd"
Next: 'b' vs 'e'. 'e' again is larger, so:
- merged = "ede"
- word1 = "bdbba", word2 = "bbbd"
Now we have a tie: 'b' vs 'b'. Hmm. There's no obvious winner. So... let’s just pick from word1. Seems harmless:
- merged = "edeb"
- word1 = "dbba", word2 = "bbbd"
Next: 'd' vs 'b'. 'd' is greater, so:
- merged = "edebd"
- word1 = "bba", word2 = "bbbd"
Again, tie: 'b' vs 'b'. We’ll stick with our earlier tie-breaking style — just pick from word1 again:
- merged = "edebdb"
- word1 = "ba", word2 = "bbbd"
Still 'b' vs 'b'. Same move:
- merged = "edebdbb"
- word1 = "a", word2 = "bbbd"
Now 'a' vs 'b'. 'b' wins:
- merged = "edebdbbb"
- word1 = "a", word2 = "bbd"
Again 'a' vs 'b'. Take 'b':
- merged = "edebdbbbb"
- word1 = "a", word2 = "bd"
Again 'a' vs 'b'. Take 'b':
- merged = "edebdbbbbb"
- word1 = "a", word2 = "d"
Now 'a' vs 'd'. 'd' wins:
- merged = "edebdbbbbbd"
- word1 = "a", word2 = ""
One letter left. We drop in 'a':
- Final result: "edebdbbbbbda"
Done. That’s twelve characters — everything accounted for. Looks decent, right? Every time, we just picked whichever character looked bigger at that moment. It felt simple. Natural.
But… is this actually the best we can do?
Something Feels Off...
Let’s sit with this result for a second: "edebdbbbbbda". Not bad. But someone tells us: “Hey, there’s actually a better version. The real best answer is this: "edebdbbbdbba".”
Wait. What?
They look so similar. You almost miss the difference. But then you spot it — somewhere in the middle, we ended up with this long streak of 'b's, and then 'd', and then 'a'. Meanwhile, the better answer breaks that streak up: it sneaks in a 'd' earlier, and delays some of those 'b's. And somehow... that gives us a bigger word overall.
So now we're wondering: why did our version fall short? We never did anything obviously wrong — we just kept picking the biggest visible letter. That felt like the right move. But maybe — maybe — that was the problem.
Are We Missing Something?
Let’s go back to one of those tie moments. Remember when we had:
- word1 = "bba"
- word2 = "bbbd"
And we saw 'b' vs 'b', and thought, “Eh, they’re the same — doesn’t matter — just take from word1.” But what if it does matter?
Let’s try looking past that first character. After the 'b's, what’s coming next in each string?
- word1 = "bba" → after the 'b', we get another 'b', then 'a'
- word2 = "bbbd" → after the 'b', another 'b', then... 'd'
Wait — 'd' is bigger than 'a'. So even though both strings started with 'b', their future is very different. If we had picked from word2 instead of word1, we’d be setting ourselves up for a stronger ending. We didn’t see that coming — we were too focused on the current character. But that tiny difference in the remaining letters actually steered the whole result in a different direction.
It makes you wonder: what if every time the letters look the same — or even close — we should be looking further ahead? Not just what letter is next, but what world are we entering if we go down this path?
That’s a much deeper question. Maybe, to truly find the best merged string, we can’t just make quick calls based on a single character. Maybe we need to peek down the road a bit.
Is it possible that choosing the best path forward isn't about picking the best right now, but about choosing the path that gives us the best later on?
We might need to rethink this whole strategy.
Rebuilding the Merge — Carefully, Step by Step
Let’s walk through the merge process with:
word1 = "ebdbba"
word2 = "debbbd"
merged = ""
Step 1:
Compare "ebdbba" vs "debbbd"
→ "ebdbba" > "debbbd"
→ Take 'e' from word1
→ merged = "e"
→ word1 = "bdbba", word2 = "debbbd"
Step 2:
Compare "bdbba" vs "debbbd"
→ "bdbba" < "debbbd"
→ Take 'd' from word2
→ merged = "ed"
→ word1 = "bdbba", word2 = "ebbbd"
Step 3:
Compare "bdbba" vs "ebbbd"
→ "bdbba" < "ebbbd"
→ Take 'e' from word2
→ merged = "ede"
→ word1 = "bdbba", word2 = "bbbd"
Step 4:
Compare "bdbba" vs "bbbd"
→ First 'b' == 'b', then 'd' > 'b'
→ "bdbba" > "bbbd"
→ Take 'b' from word1
→ merged = "edeb"
→ word1 = "dbba", word2 = "bbbd"
Step 5:
Compare "dbba" vs "bbbd"
→ 'd' > 'b'
→ "dbba" > "bbbd"
→ Take 'd' from word1
→ merged = "edebd"
→ word1 = "bba", word2 = "bbbd"
Step 6:
Compare "bba" vs "bbbd"
→ 'b' == 'b', 'b' == 'b', 'a' < 'd'
→ "bba" < "bbbd"
→ Take 'b' from word2
→ merged = "edebdb"
→ word1 = "bba", word2 = "bbd"
Step 7:
Compare "bba" vs "bbd"
→ 'b' == 'b', 'b' == 'b', 'a' < 'd'
→ "bba" < "bbd"
→ Take 'b' from word2
→ merged = "edebdbb"
→ word1 = "bba", word2 = "bd"
Step 8:
Compare "bba" vs "bd"
→ 'b' == 'b', 'b' > 'd'
→ "bba" > "bd"
→ Take 'b' from word1
→ merged = "edebdbbb"
→ word1 = "ba", word2 = "bd"
Step 9:
Compare "ba" vs "bd"
→ 'b' == 'b', 'a' < 'd'
→ "ba" < "bd"
→ Take 'b' from word2
→ merged = "edebdbbbd"
→ word1 = "ba", word2 = "d"
Step 10:
Compare "ba" vs "d"
→ 'b' < 'd'
→ "ba" < "d"
→ Take 'd' from word2
→ merged = "edebdbbbdb"
→ word1 = "ba", word2 = ""
Step 11:
word2 is empty — append the rest of word1: "ba"
→ Final result: "edebdbbbdbba"
Final Answer: "edebdbbbdbba"
That’s It — The True Largest Merge
And now we’ve got it. The biggest, boldest, most lexicographically “late” string we can make from these two words:
"edebdbbbdbba"
And what’s wild is, we didn’t do anything radical. We just… paused. Looked ahead. Asked smarter questions at each fork in the road.
Turns out, that single-character comparison — the strategy that seemed so safe — wasn’t enough. It missed the big picture. Because choosing the better-looking step isn’t the same as choosing the better path.
Sometimes the next letter isn’t the most important thing. Sometimes it’s the rest of the story that really decides how far you go.
Well wrapped up! Now, if you take a step back and ask — what kind of thinking are we actually doing here?
We’re making the best possible choice at each step by looking at both remaining strings and choosing the one that gives us the better future. We're not trying out every possible way to merge them — just making smart decisions as we go.
And that kind of thinking? It lines up perfectly with what’s known as a greedy strategy.
Exactly — in this case, the approach works beautifully because at every point, we're steering the result toward the best possible outcome without needing to brute-force every merge. We're not guessing — we're just paying attention to what comes next, and that’s enough.
Let's now see how our algorithm looks!
Largest Merge Of Two Strings Algorithm
We implement a Largest Merge Of Two Strings solution using a greedy approach.
- We start by initializing a StringBuilder named merge, which will store the final merged result.
- We also set up two pointers, i and j, to keep track of our current positions in word1 and word2.
- As long as there are still characters left in both words:
- We compare the remaining suffixes starting at word1[i] and word2[j].
- If the suffix from word1 is lexicographically larger, we take word1[i], append it to merge, and move i forward.
- Otherwise, we take word2[j], append it to merge, and move j forward.
- Once one word runs out, we simply append whatever is left of the other word to the end of merge.
- Finally, we return the full merged string we've built.
Approach
- Initialize:
- A StringBuilder called merge to build the result.
- Two pointers i and j to track current positions in word1 and word2.
- While neither string is exhausted:
- Compare the remaining suffixes word1[i:] and word2[j:].
- If word1[i:] is greater, append word1[i] to merge and increment i.
- Otherwise, append word2[j] to merge and increment j.
- Once one word is fully consumed: Append the rest of the other word to merge.
- Return: Return the merged string as the result.

Dry-Run
Input: word1 = "cbacba", word2 = "cbcba"
We’re building a result string by always comparing the remaining suffixes of word1[i:] and word2[j:], and taking the first character from the larger one (in lexicographic terms).
Step 1:
word1 = "cbacba"
word2 = "cbcba"
Compare: "cbacba" vs "cbcba"
→ "cbcba" is greater → take 'c' from word2
Merged: "c"
Step 2:
word1 = "cbacba"
word2 = "bcba"
Compare: "cbacba" vs "bcba"
→ "cbacba" is greater → take 'c' from word1
Merged: "cc"
Step 3:
word1 = "bacba"
word2 = "bcba"
Compare: "bacba" vs "bcba"
→ "bcba" is greater → take 'b' from word2
Merged: "ccb"
Step 4:
word1 = "bacba"
word2 = "cba"
Compare: "bacba" vs "cba"
→ "cba" is greater → take 'c' from word2
Merged: "ccbc"
Step 5:
word1 = "bacba"
word2 = "ba"
Compare: "bacba" vs "ba"
→ "bacba" is greater → take 'b' from word1
Merged: "ccbcb"
Step 6:
word1 = "acba"
word2 = "ba"
Compare: "acba" vs "ba"
→ "ba" is greater → take 'b' from word2
Merged: "ccbcbb"
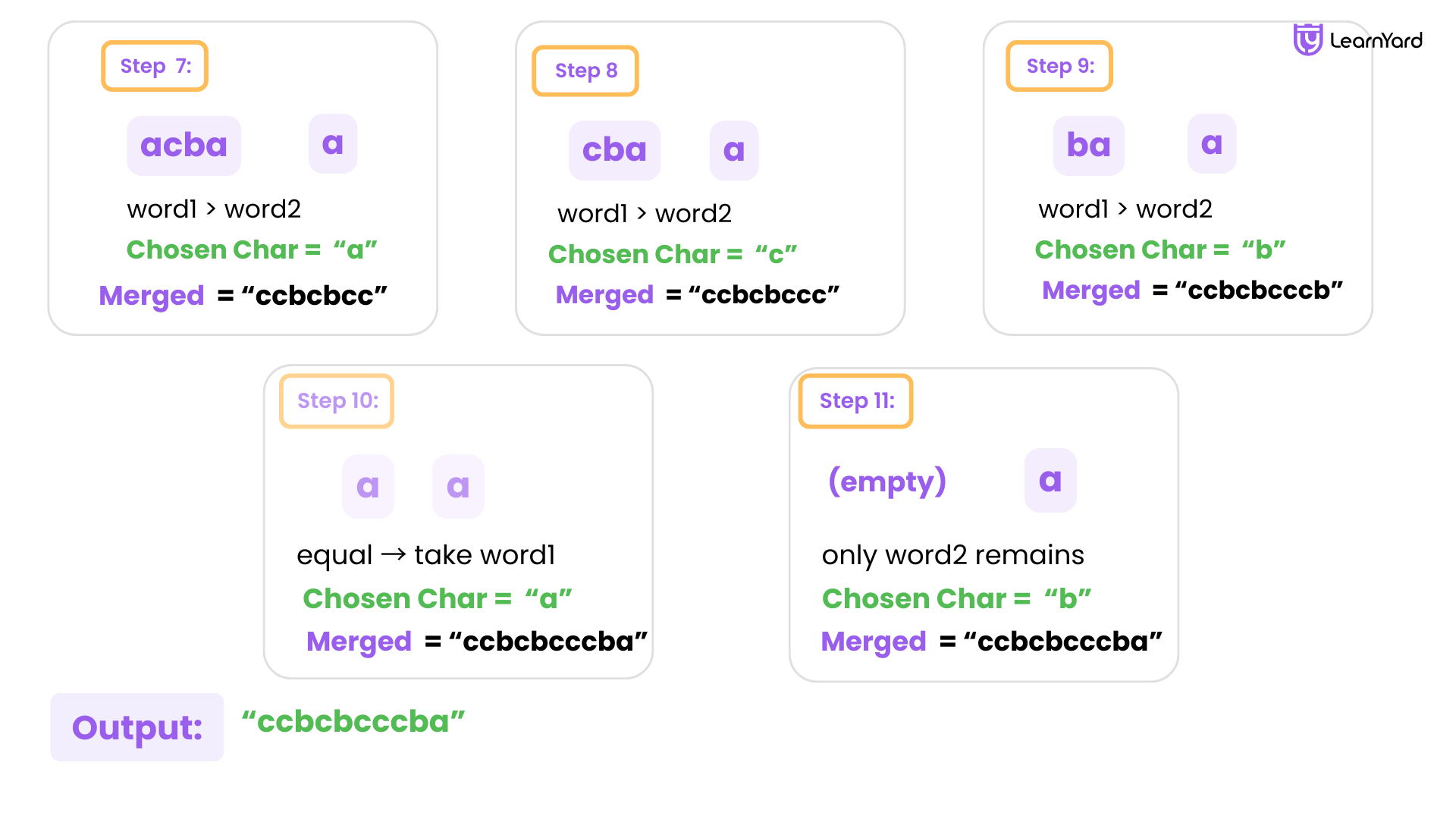
Step 7:
word1 = "acba"
word2 = "a"
Compare: "acba" vs "a"
→ "acba" is greater → take 'a' from word1
Merged: "ccbcbba"
Step 8:
word1 = "cba"
word2 = "a"
Compare: "cba" vs "a"
→ "cba" is greater → take 'c' from word1
Merged: "ccbcbbac"
Step 9:
word1 = "ba"
word2 = "a"
Compare: "ba" vs "a"
→ "ba" is greater → take 'b' from word1
Merged: "ccbcbbacb"
Step 10:
word1 = "a"
word2 = "a"
Compare: "a" vs "a"
→ equal → doesn't matter, compare suffixes: "a" vs "a" → equal → can take from either → take from word1
Merged: "ccbcbbacba"
Step 11:
word1 = ""
word2 = "a"
Only word2 remains → append it
Merged: "ccbcbbacbaa"
Final Merged String: "ccbcbbacbaa"
Largest Merge Of Two Strings Solution
Now let's checkout the "Largest Merge Of Two Strings" in C++, Java, Python and JavaScript.
"Largest Merge Of Two Strings" Code in all Languages.
1. Largest Merge Of Two Strings solution in C++ Try on Compiler
class Solution {
public:
// Function to create the lexicographically largest merge
string largestMerge(string word1, string word2) {
// Result string to store merge
string merge;
// While both strings have characters left
while (!word1.empty() && !word2.empty()) {
// Compare suffixes and pick the larger one
if (word1 > word2) {
merge += word1[0];
word1.erase(0, 1);
} else {
merge += word2[0];
word2.erase(0, 1);
}
}
// Append remaining characters from word1
merge += word1;
// Append remaining characters from word2
merge += word2;
return merge;
}
};2. Largest Merge Of Two Strings Solution in Java Try on Compiler
class Solution {
// Function to create the lexicographically largest merge
public String largestMerge(String word1, String word2) {
// StringBuilder to efficiently build the result
StringBuilder merge = new StringBuilder();
// Pointers for both words
int i = 0, j = 0;
// Process until one string is exhausted
while (i < word1.length() && j < word2.length()) {
// Compare suffixes from i and j onwards
if (word1.substring(i).compareTo(word2.substring(j)) > 0) {
merge.append(word1.charAt(i++));
} else {
merge.append(word2.charAt(j++));
}
}
// Append remaining part of word1 if any
merge.append(word1.substring(i));
// Append remaining part of word2 if any
merge.append(word2.substring(j));
return merge.toString();
}
}3. Largest Merge Of Two Strings Solution in Python Try on Compiler
class Solution:
# Function to create the lexicographically largest merge
def largestMerge(self, word1: str, word2: str) -> str:
# Result list for efficient concatenation
merge = []
# While both strings are non-empty
while word1 and word2:
# Compare entire suffixes and pick larger
if word1 > word2:
merge.append(word1[0])
word1 = word1[1:]
else:
merge.append(word2[0])
word2 = word2[1:]
# Append remaining characters from word1
merge.extend(word1)
# Append remaining characters from word2
merge.extend(word2)
return ''.join(merge)4. Largest Merge Of Two Strings solution in JavaScript Try on Compiler
/**
* @param {string} word1
* @param {string} word2
* @return {string}
*/
var largestMerge = function(word1, word2) {
// Result string to accumulate characters
let merge = "";
// While both strings are non-empty
while (word1.length && word2.length) {
// Compare entire suffixes and choose larger
if (word1 > word2) {
merge += word1[0];
word1 = word1.slice(1);
} else {
merge += word2[0];
word2 = word2.slice(1);
}
}
// Append any leftover from word1
merge += word1;
// Append any leftover from word2
merge += word2;
return merge;
};Largest Merge Of Two Strings Complexity Analysis
Time Complexity: O(n x k)
The Largest Merge algorithm involves two key operations:
- Iterating through both strings while comparing suffixes:
We use two pointers to traverse word1 and word2. At each step, we compare the suffixes starting from these pointers to decide which character to append next.
This ensures we always pick the lexicographically larger suffix’s current character.
Since each character is appended exactly once, the loop runs at most len(word1) + len(word2) times. - Appending leftover characters after one string is exhausted:
Once one string is fully consumed, we append the remaining part of the other string to the merge.
This step takes linear time proportional to the leftover length.
Thus, the overall time complexity is dominated by the suffix comparisons inside the loop, making it approximately: O(n×k)
where
- n = total length of word1 and word2
- k = average length of suffix comparisons done at each step
Space Complexity: O(n)
Auxiliary Space Complexity: Auxiliary space refers to the extra space required by the algorithm excluding the input.
- Result builder: We use a StringBuilder (or equivalent) to store the merged result, which can grow up to size O(n), where n = len(word1) + len(word2).
- Suffix comparisons: Although we use suffixes like word1[i:] and word2[j:] for comparisons, these are views/references and do not create new copies in optimized implementations, so their space usage is O(1).
- Pointers and counters: We maintain two pointers (i and j) and a few other variables, which use constant space O(1).
Thus, the auxiliary space complexity is O(n + 1) = O(n).
Total Space Complexity:
- Input strings word1 and word2 occupy O(len(word1) + len(word2)) = O(n) space.
- Extra space (result builder + variables) is O(n) as explained above.
Hence, the total space complexity is O(n).
Similar Problems
You are given a 0-indexed integer array players, where players[i] represents the ability of the ith player. You are also given a 0-indexed integer array trainers, where trainers[j] represents the training capacity of the jth trainer.
The ith player can match with the jth trainer if the player's ability is less than or equal to the trainer's training capacity. Additionally, the ith player can be matched with at most one trainer, and the jth trainer can be matched with at most one player.
Return the maximum number of matchings between players and trainers that satisfy these conditions.
You are given a 0-indexed array words containing n strings.
Let's define a join operation join(x, y) between two strings x and y as concatenating them into xy. However, if the last character of x is equal to the first character of y, one of them is deleted.
For example join("ab", "ba") = "aba" and join("ab", "cde") = "abcde".
You are to perform n - 1 join operations. Let str0 = words[0]. Starting from i = 1 up to i = n - 1, for the ith operation, you can do one of the following:
- Make stri = join(stri - 1, words[i])
- Make stri = join(words[i], stri - 1)
Your task is to minimize the length of strn - 1.
Return an integer denoting the minimum possible length of strn - 1.