Kth Missing Positive Number Solution In C++/Java/Python/JS
Problem Description:
Given an array arr of positive integers sorted in a strictly increasing order, and an integer k.
Return the k-th positive integer that is missing from this array.
Examples:
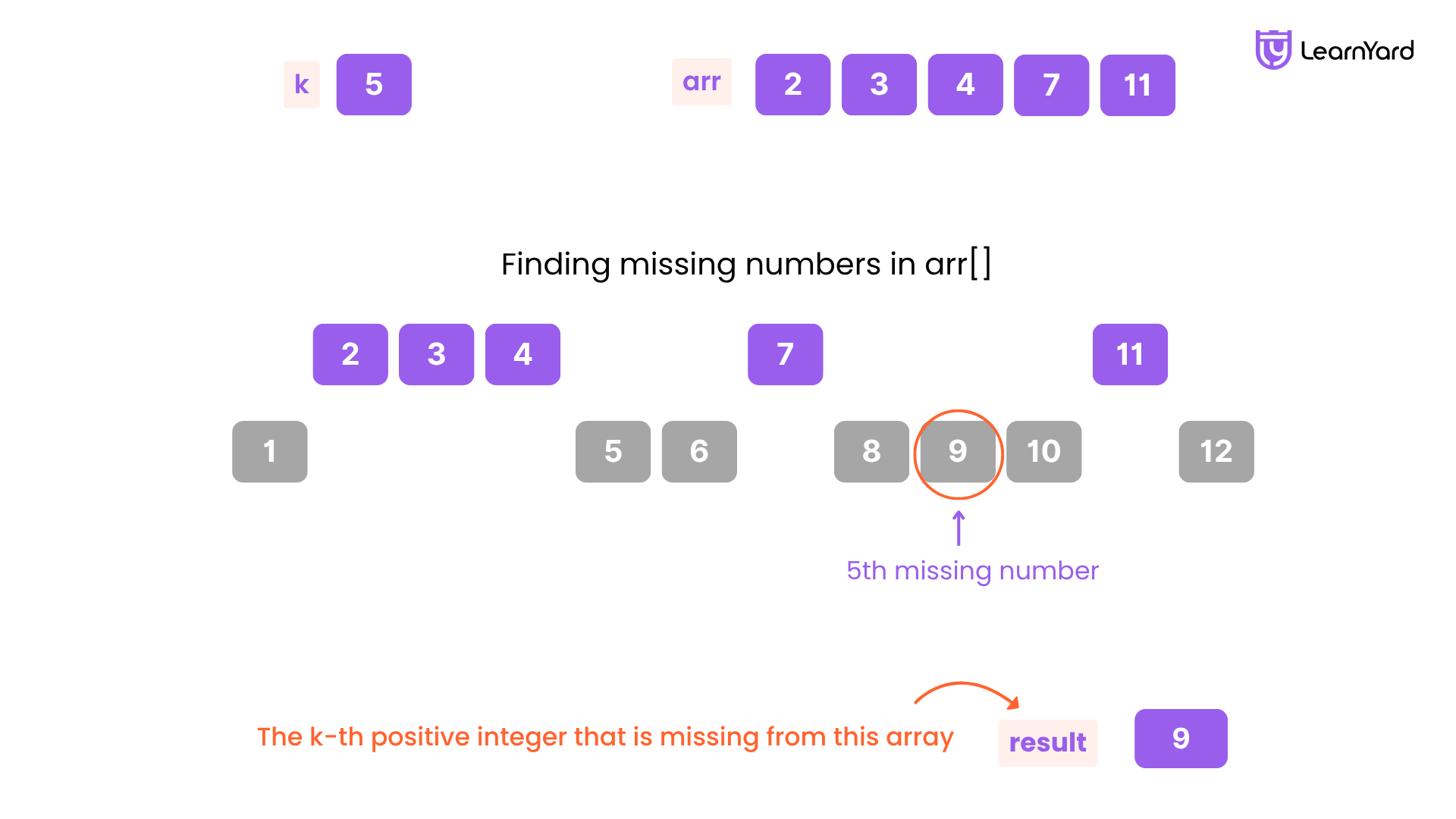
Input: arr = [2, 3, 4, 7, 11], k = 5
Output: 9
Explanation: The missing positive integers are [1, 5, 6, 8, 9, 10, 12, 13, ...]. The 5th missing positive integer is 9.
Input: arr = [1, 2, 3, 4], k = 2
Output: 6
Explanation: The missing positive integers are [5, 6, 7, ...]. The 2nd missing positive integer is 6.
Constraints:
1 <= arr.length <= 1000
1 <= arr[i] <= 1000
1 <= k <= 1000
arr[i] < arr[j] for 1 <= i < j <= arr.length
Brute Force Approach
Okay, so here's the thought process:
What comes to mind after reading the problem statement?
We need to find the k-th missing positive integer from the given sorted array. To approach this problem, we need to consider both present and missing numbers. Here's a simple and systematic approach.
First, observe the sequence of numbers and the gaps between them. For instance, in the array [2, 3, 4, 7, 11], the missing numbers are [1, 5, 6, 8, 9, 10, 12, 13, ...]. The 5th missing number is 9.
Similarly, in the array [1, 2, 3, 4], the missing numbers are [5, 6, 7, ...]. The 2nd missing number is 6.
This observation helps us identify the pattern and limits the range we need to track.
One straightforward solution is to traverse the sequence starting from 1 and count how many numbers are missing.
To find the kth missing positive number efficiently, we can use a two-pointer approach that aligns with the natural sequence and the given sorted array. Imagine the natural number sequence starting from 1.
As we iterate through this sequence, we'll use one pointer (i) to track the current number in the natural sequence and another pointer (j) to track elements in the given array. The idea is straightforward — if the current number matches the element in the array (i.e., arr[j] == i), it’s not missing, so we move both pointers forward. However, if the current number does not match the element in the array, that number is missing, so we increment a missing count. We continue this process until the missing count reaches k.
For example, consider the array [2, 3, 4, 7, 11] and k = 5. Starting with i = 1 and j = 0, the first missing number is 1. As we proceed, numbers 2, 3, and 4 are found in the array, so we skip them.
The next missing numbers are 5, 6, 8, and 9. Once we reach the 5th missing number (which is 9), we stop. If the array ends before reaching k missing numbers, we can directly compute the remaining missing numbers by extending the sequence beyond the last element of the array.
Let's understand with an example:
Kth Missing Positive Number Example :
Input: arr = [2, 3, 4, 7, 11], k = 5
Step 1: Initialize count = 0, i = 1, j = 0
- i = 1, arr[j] = 2 → 1 is missing → count = 1
- i = 2, arr[j] = 2 → 2 is present → Move j to 1
- i = 3, arr[j] = 3 → 3 is present → Move j to 2
- i = 4, arr[j] = 4 → 4 is present → Move j to 3
- i = 5, arr[j] = 7 → 5 is missing → count = 2
- i = 6, arr[j] = 7 → 6 is missing → count = 3
- i = 7, arr[j] = 7 → 7 is present → Move j to 4
- i = 8, arr[j] = 11 → 8 is missing → count = 4
- i = 9, arr[j] = 11 → 9 is missing → count = 5
Since count = k, the loop stops, and the result is i - 1 = 9.
Final Answer: 9
How to code it up:
- Initialize Variables:
- count = 0 → Tracks the number of missing integers found.
- i = 1 → Starts checking from the first positive integer.
- j = 0 → Points to the current index in the array.
- Iterate Until Conditions Met:
- While j < array size and count < k:
- If array[j] == i → Number is present, move to the next element (j++).
- Else → Number is missing, increment count.
- Always increment i to check the next integer.
- Return Result:
- If count == k → Return i - 1 (the k-th missing number).
- Else → Return last element in array + k - count (remaining missing numbers appear after the array ends).
Kth Missing Positive Number Solution
Code Implementation
1. Kth Missing Positive Number Leetcode Solution C++ Try on Compiler
class Solution {
public:
int findKthPositive(vector<int>& arr, int k) {
// Initialize count to track missing numbers
int count = 0;
// Start checking numbers from 1
int i = 1;
// Initialize pointer to traverse the array
int j = 0;
// Iterate until either the array is exhausted or k missing numbers are found
while (j < arr.size() && count < k) {
// If the current number matches the array element
if (arr[j] == i) {
// Move to the next element in the array
j++;
}
else {
// Otherwise, it's a missing number; increment count
count++;
}
// Move to the next number
i++;
}
// If exactly k missing numbers are found, return the last identified missing number
if (count == k)
return i - 1;
// Otherwise, compute the remaining missing numbers after the array ends
return arr.back() + k - count;
}
};
2. Kth Missing Positive Number Leetcode Solution Java Try on Compiler
class Solution {
public int findKthPositive(int[] arr, int k) {
// Initialize count to track missing numbers
int count = 0;
// Start checking numbers from 1
int i = 1;
// Initialize pointer to traverse the array
int j = 0;
// Iterate until either the array is exhausted or k missing numbers are found
while (j < arr.length && count < k) {
// If the current number matches the array element
if (arr[j] == i) {
// Move to the next element in the array
j++;
}
else {
// Otherwise, it's a missing number; increment count
count++;
}
// Move to the next number
i++;
}
// If exactly k missing numbers are found, return the last identified missing number
if (count == k)
return i - 1;
// Otherwise, compute the remaining missing numbers after the array ends
return arr[arr.length - 1] + k - count;
}
}
3. Kth Missing Positive Number Leetcode Solution Python Try on Compiler
class Solution:
def findKthPositive(self, arr, k):
# Initialize count to track missing numbers
count = 0
# Start checking numbers from 1
i = 1
# Initialize pointer to traverse the array
j = 0
# Iterate until either the array is exhausted or k missing numbers are found
while j < len(arr) and count < k:
# If the current number matches the array element
if arr[j] == i:
# Move to the next element in the array
j += 1
else:
# Otherwise, it's a missing number; increment count
count += 1
# Move to the next number
i += 1
# If exactly k missing numbers are found, return the last identified missing number
if count == k:
return i - 1
# Otherwise, compute the remaining missing numbers after the array ends
return arr[-1] + k - count
4. Kth Missing Positive Number Leetcode Solution Javascript Try on Compiler
var findKthPositive = function(arr, k) {
// Initialize count to track missing numbers
let count = 0;
// Start checking numbers from 1
let i = 1;
// Initialize pointer to traverse the array
let j = 0;
// Iterate until either the array is exhausted or k missing numbers are found
while (j < arr.length && count < k) {
// If the current number matches the array element
if (arr[j] === i) {
// Move to the next element in the array
j++;
}
else {
// Otherwise, it's a missing number; increment count
count++;
}
// Move to the next number
i++;
}
// If exactly k missing numbers are found, return the last identified missing number
if (count === k)
return i - 1;
// Otherwise, compute the remaining missing numbers after the array ends
return arr[arr.length - 1] + k - count;
};
Complexity Analysis for Kth Missing Positive Number LeetCode Solution
Time Complexity: O(n + k)
The given approach essentially iterates through the array and the missing numbers between elements. Let's break down the key steps and analyze their time complexity.
Key Observations
- Pointer j Traverses the Array:
- The pointer j only moves forward when an element in the array matches the current number i.
- Therefore, j will iterate through all elements in the array once, resulting in O(n) steps where n is the length of the array.
- Pointer i Traverses Numbers Sequentially:
- The pointer i continues incrementing even when numbers are missing.
- In the worst case, the algorithm may need to check numbers until the k-th missing number is found.
- This requires iterating up to arr[n-1] + k in the worst case.
The worst-case occurs when all numbers in the range 1 to k are missing. For example:
Input: arr = [1000], k = 999. The loop would iterate through numbers from 1 to 999 to reach the k-th missing number.
So, the total number of iterations is max(n, arr[n-1] + k).
Since the loop iterates both:
1. Up to arr[n-1] elements in the array (O(n))
2. Plus additional steps to count remaining missing numbers (O(k))
The final complexity is: O(n + k)
Space Complexity: O(n)
Auxiliary Space Complexity: O(1 )
Explanation: We are only using a few integer variables — count, i, and j — to track the missing numbers and array traversal. No additional data structures like arrays or lists are used.
Thus, the auxiliary space complexity is O(1), as only a constant amount of extra space is required.
Total Space Complexity: O(n)
Explanation: The input array arr is provided as an argument, and no extra space is allocated for new data structures during execution.
Therefore, the total space used by the algorithm is O(n).
Will Brute Force Work Against the Given Constraints?
For the current solution with O(n + k) time complexity, the approach efficiently handles the given constraints.
Since the maximum possible value for n (array length) is 1000, and the maximum possible value for k is also 1000, the solution may require up to 2000 steps in the worst case.
In competitive programming environments, problems typically handle up to 10⁶ operations per test case. With a maximum of 2000 steps, the solution easily fits these limits.
Therefore, the O(n + k) time complexity ensures the solution works efficiently within the given problem constraints and will not result in Time Limit Exceeded (TLE) errors, even when handling maximum input values.
Can we optimize it?
Let's look at optimizing the Kth Missing Positive Number solution further.
In our previous solution, we iterated over values until we counted k missing numbers, which resulted in O(n + k) time complexity. Now, we want to make this process more efficient.
We know that the missing positive integers follow a predictable pattern. For each index i, the number of missing positive integers before arr[i] can be calculated using this formula:
Missing Numbers Before arr[i] = arr[i] - (i + 1)
For example:
- In arr = [2, 3, 4, 7, 11], at index 0, there’s 1 missing number before arr[0] (since 2 - (0 + 1) = 1).
- At index 3, there are 3 missing numbers before arr[3] (since 7 - (3 + 1) = 3).
Using this observation, we can now use a more efficient approach.
Let's Make a Few More Observations
To solve the problem efficiently, we can identify some key properties about the array and the missing numbers:
- The Array is Sorted:
The given array arr is sorted in strictly increasing order.
➔ This sorted property allows us to confidently divide the array into two halves and decide which half might contain the kth missing number. - The Search Space is Monotonic:
The count of missing numbers strictly increases as we move forward in the array.
➔ This monotonic behavior ensures that once a portion of the array is ruled out, the target cannot exist in that discarded part. - The middle element helps minimize or maximize the search space:
For any element arr[mid], the number of missing positive integers before it can be calculated using the formula:
Missing Numbers Before arr[mid] is equal to arr[mid] - (mid + 1)
➔ If this value is less than k, the kth missing number must be in the right half.
➔ If this value is greater than or equal to k, the kth missing number must be in the left half.
This observation helps us efficiently decide which half of the array to search.
Since we've seen that the array is sorted, the number of missing elements increases steadily, and we can efficiently decide which half to search based on the count of missing numbers — this aligns perfectly with the conditions for applying binary search. So, we can now use binary search to efficiently locate the kth missing number.
To apply binary search in this problem, we can build the logic based on key observations.
Kth Missing Positive Number Binary Search Algorithm
First, notice that if no elements were missing, the sequence would follow the pattern [1, 2, 3, 4, ...]. However, since some numbers are missing, each element in the given array effectively shifts the sequence forward by a certain number of values.
For any element arr[i], the number of missing elements before it can be calculated as arr[i] - (i + 1). This formula works because arr[i] is the actual number at index i, while (i + 1) is what the value should have been if no numbers were missing. The difference between these two gives the count of missing numbers up to that point.
Using this observation, we can efficiently determine where the kth missing number lies. If the count of missing numbers before arr[mid] is less than k, the kth missing number must be in the right half of the array. Conversely, if the count of missing numbers before arr[mid] is greater than or equal to k, the kth missing number must be on the left side or could even be arr[mid] itself.
Once the binary search ends, the pointer low will represent the position where the kth missing number would have been if no numbers were missing. However, since the given array arr skips some numbers, we must compensate for those missing values.
In an ideal scenario where no numbers were missing, the index position and the actual value at that position would be the same (e.g., position 3 would hold the value 3). However, because numbers are missing, the value at low is actually smaller than expected.
To adjust for these missing numbers, we recognize that the number of missing values before position low is exactly k. Since each missing number shifts our expected value by one, we can determine the correct kth missing number by adding k to low. This effectively shifts our position forward by the exact amount needed to land on the kth missing value.
Thus, the final answer can be calculated as low + k, ensuring we correctly identify the kth missing number without scanning each element individually.
Let us understand this with a video,
Understand with an example:
Kth Missing Positive Number Example:
Let's dry run the binary search approach with the example:
Input: arr = [2, 3, 4, 7, 11], k = 5
Missing numbers: [1, 5, 6, 8, 9, 10, 12, ...]
Step 1: Initial Setup
- low = 0, high = 4 (array indices)
Step 2: First Binary Search Iteration
- mid = (0 + 4) / 2 = 2
- Missing numbers before arr[2] = 4 → 4 - (2 + 1) = 1
- Since 1 < k, the kth missing number must be on the right side.
- low = mid + 1 = 3
Step 3: Second Binary Search Iteration
- mid = (3 + 4) / 2 = 3
- Missing numbers before arr[3] = 7 → 7 - (3 + 1) = 3
- Since 3 < k, the kth missing number must be on the right side.
- low = mid + 1 = 4
Step 4: Third Binary Search Iteration
- mid = (4 + 4) / 2 = 4
- Missing numbers before arr[4] = 11 → 11 - (4 + 1) = 5
- Since 5 ≥ k, the kth missing number could be here or on the left side.
- high = mid - 1 = 3
Step 5: Binary Search Ends
- low = 4, high = 3
- Binary search stops when low > high.
Step 6: Calculate the Final Answer
- The kth missing number is low + k = 4 + 5 = 9.
Output: 9
How to code it up?
Initialize Pointers:
Set low = 0 and high = n - 1 (where n is the size of the array).
Binary Search Logic:
- Calculate mid = low + (high - low) / 2.
- Check the number of missing numbers before arr[mid] using the formula:
Missing Numbers Before arr[mid] = arr[mid] - (mid + 1) - If the number of missing numbers before arr[mid] is less than k, move to the right half by setting low = mid + 1.
- If the number of missing numbers before arr[mid] is greater than or equal to k, move to the left half by setting high = mid - 1.
Termination Condition:
The binary search loop will end when low > high. At this point:
- The kth missing number is given by the formula:
kth Missing Number = low + k
Kth Missing Positive Number Solution
Kth Missing Positive Number leetcode solution / Code Implementation
1. Kth Missing Positive Number Leetcode Solution C++ Try on Compiler
class Solution {
public:
int findKthPositive(vector<int>& arr, int k) {
// Initialize binary search boundaries
int low = 0, high = arr.size() - 1;
// Binary Search Loop
while (low <= high) {
int mid = low + (high - low) / 2;
// Count missing numbers before arr[mid]
int missingCount = arr[mid] - (mid + 1);
if (missingCount < k)
low = mid + 1; // Search on the right side
else
high = mid - 1; // Search on the left side
}
// Final calculation for the kth missing number
return low + k;
}
};
2. Kth Missing Positive Number Leetcode Solution Java Try on Compiler
class Solution {
public int findKthPositive(int[] arr, int k) {
// Initialize binary search boundaries
int low = 0, high = arr.length - 1;
// Binary Search Loop
while (low <= high) {
int mid = low + (high - low) / 2;
// Count missing numbers before arr[mid]
int missingCount = arr[mid] - (mid + 1);
if (missingCount < k)
low = mid + 1; // Search on the right side
else
high = mid - 1; // Search on the left side
}
// Final calculation for the kth missing number
return low + k;
}
}
3. Kth Missing Positive Number Leetcode Solution Python Try on Compiler
class Solution:
def findKthPositive(self, arr, k):
# Initialize binary search boundaries
low, high = 0, len(arr) - 1
# Binary Search Loop
while low <= high:
mid = low + (high - low) // 2
# Count missing numbers before arr[mid]
missingCount = arr[mid] - (mid + 1)
if missingCount < k:
low = mid + 1 # Search on the right side
else:
high = mid - 1 # Search on the left side
# Final calculation for the kth missing number
return low + k
4. Kth Missing Positive Number Leetcode Solution Javascript Try on Compiler
var findKthPositive = function(arr, k) {
// Initialize binary search boundaries
let low = 0, high = arr.length - 1;
// Binary Search Loop
while (low <= high) {
let mid = Math.floor(low + (high - low) / 2);
// Count missing numbers before arr[mid]
let missingCount = arr[mid] - (mid + 1);
if (missingCount < k)
low = mid + 1; // Search on the right side
else
high = mid - 1; // Search on the left side
}
// Final calculation for the kth missing number
return low + k;
};
Complexity Analysis for Kth Missing Positive Number LeetCode Solution
Time Complexity: O(log n)
Step 1: Binary Search Iterations
- In each iteration, the binary search algorithm reduces the search space by half.
- This halving process continues until only one element remains.
- Since the array has n elements, the number of iterations is O(log n).
Step 2: Missing Number Calculation
- After exiting the binary search loop, the final step involves computing the result using the formula:
low + k - This calculation is constant time, i.e., O(1).
Final Time Complexity: O(log n)
Space Complexity: O(n)
Auxiliary Space Complexity: O(1)
Explanation: The space complexity of this solution is O(1) because we only use a few variables such as low, high, mid, and missingCount to store intermediate results. No additional data structures are used that grow with the size of the input.
Total Space Complexity: O(1)
Explanation: The input array arr is provided as an argument, and no extra space is allocated for new data structures during execution.
Therefore, the total space used by the algorithm is O(n).
Similar Problems
The Kth Missing Positive Number problem requires identifying the kth missing integer in a sorted array of distinct positive numbers. A straightforward approach is to find the kth missing number by iterating through the array while counting missing values. However, a more efficient method involves using Binary Search to quickly determine where the missing numbers accumulate. By leveraging properties of a sorted array, we can optimize the search and reduce the time complexity significantly. This problem is commonly encountered in coding challenges where efficient searching techniques are required.
Now that we have successfully tackled this problem, let's try similar problems.
You are given an integer array nums and an integer k. Append k unique positive integers that do not appear in nums to nums such that the resulting total sum is minimum.
Return the sum of the k integers appended to nums.