Kth Bit is Set or Not Solution In C++/Java/Python/JS
Problem Description
Given two positive integer n and k, check if the kth index bit of n is set or not.
What is a Kth Bit and Set Bit?
What is the k-th bit?
Every number in binary is made up of bits (0s and 1s). These bits are like positions in a list:
- The rightmost bit is the 1st bit (Least Significant Bit or LSB),
- The next is the 2nd bit, and so on until the 32nd bit (since it's a 32-bit number).
Example:
Take the number 70. In binary, it is 1000110. From right to left, the bits are:
- Bit-1 = 0
- Bit-2 = 1
- Bit-3 = 1
- Bit-4 = 0
- Bit-5 = 0
- Bit-6 = 0
- Bit-7 = 1
So the 3rd bit (from the right) is 1.
“Is the k-th bit of n set?”, it's really asking: Is the digit at position k in the binary representation of n a 1?
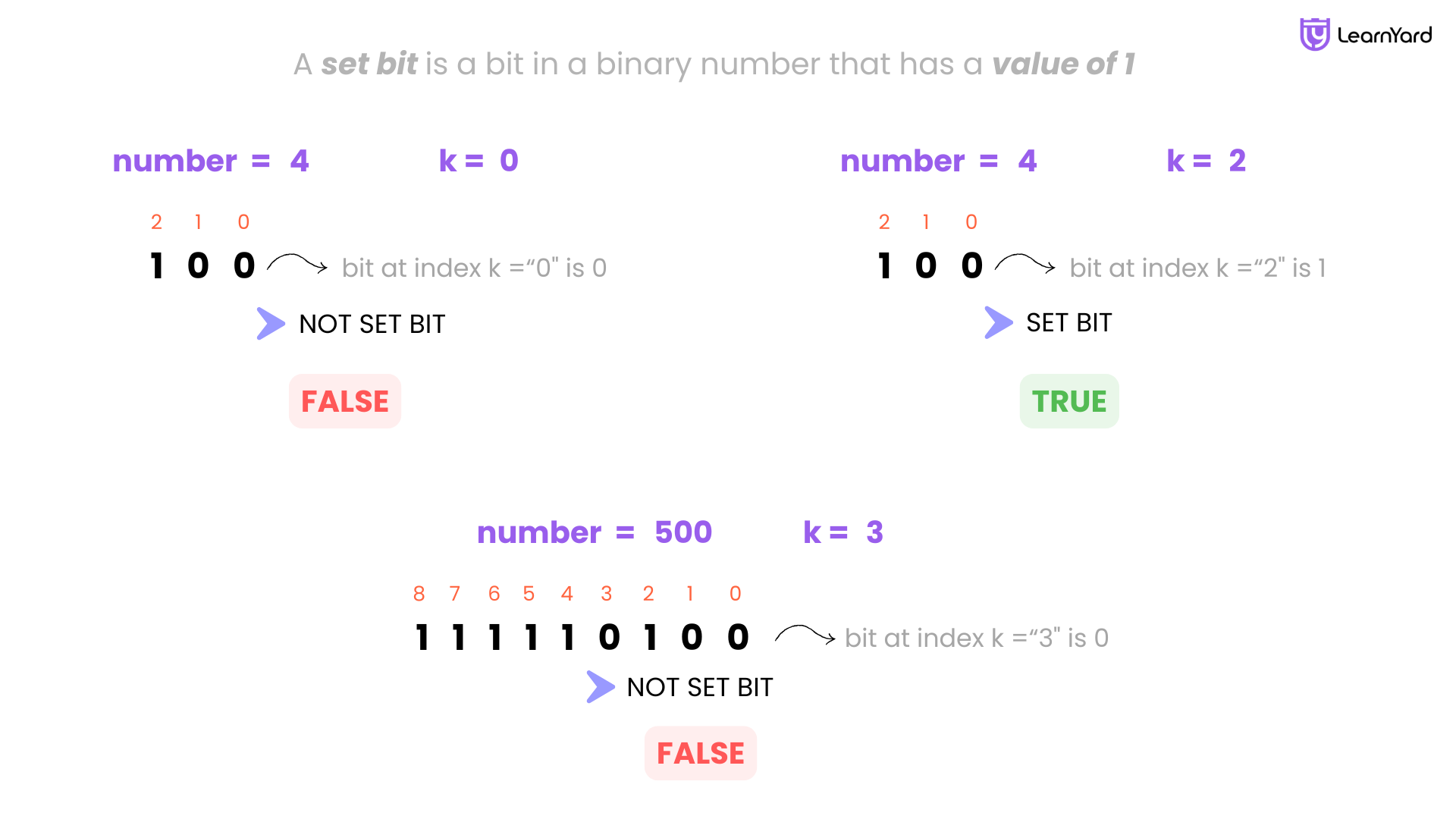
Example
Input: n = 4, k = 0
Output: false
Explanation: Binary representation of 4 is 100, in which 0th index bit from LSB is not set. So, return false.
Input: n = 4, k = 2
Output: true
Explanation: Binary representation of 4 is 100, in which 2nd index bit from LSB is set. So, return true.
Input: n = 500, k = 3
Output: false
Explanation: Binary representation of 500 is 111110100, in which 3rd index bit from LSB is not set. So, return false.
Constraints
- 1 <= n <= 10^9
- 0 <= i <= 31
Think of a number as a sequence of bits lined up, each one holding a small but critical piece of information. Now imagine if we had direct control to read any specific bit i.e. if it is 0 or 1 —how powerful would that be while working at the lowest level of data?
Optimal Approach
Intuition
The main idea is to find how do we isolate a single bit from a number and check if it is set (i.e., it is 1)?. We create a mask where only the i-th bit is 1, and the rest are 0, using 1 << i.
What is Mask and Left Shift (<<) Operator?
A mask is simply a number that helps us focus on specific bits within another number. Think of it like using a stencil when painting — the stencil (mask) allows us to paint only in specific areas and ignore the rest. Similarly, in programming, a bitmask helps us isolate, set, or clear particular bits in a number.
But the mask has to be smartly constructed — it should have a 1 only at the position we care about and 0 everywhere else.
For example, if we want to work with the 3rd bit (from the right), we make a mask like this:
00000100 (which is 4 in decimal) — this has 1 only at the 3rd position and zeroes elsewhere.
This kind of mask helps us target the 3rd bit only, without disturbing others.
What is the Left Shift (<<) Operator?
The Left Shift (<<) operator is how we create such masks or shift bits to the left.
Here’s what happens when we do something like:
1 << 3
Let’s understand this step-by-step:
- Start with the number 1 → in binary: 00000001
- Shift it 3 positions to the left → becomes 00001000
- This is now 8 in decimal.
So, doing 1 << i creates a number where only the i-th bit is 1 and the rest are 0s.
That’s exactly what we want in a mask when we want to work with the i-th bit.
Then we use bitwise AND (&) with the original number. Why? Because AND only returns 1 when both bits are 1. So if the k-th bit of n is also 1, then the result of n & mask will be non-zero. Otherwise, it will be 0.
If the result is non-zero, it means the bit was 1.
If the result is zero, it means the bit was 0.
Example:
Let’s say our number is 13, and we want to check the 2nd bit (i = 2).
- Binary of 13: 1101
- Mask: 1 << 2 = 0100 (which is 4)
- Now do: 1101 & 0100 = 0100 (which is 4, non-zero)
So, the 2nd bit is set (it's 1).
Approach
Step 1: Create a Bit Mask to Target the k-th Bit
To check whether the k-th bit is set, we first need to create a mask that has 1 only at the k-th position, and 0s elsewhere.
This is done using the left shift operation:
mask = 1 << k
This places the binary 1 exactly at the k-th position.
Step 2: Perform Bitwise AND Operation
Use the bitwise AND operation between the number n and the mask:
n & mask
- If the result is 0, it means the k-th bit is not set (bit is 0).
- If the result is non-zero, the k-th bit is set (bit is 1).
Step 3: Use if-else to Return True or False
Check the result of the AND operation and return:
- false if the result is 0 (bit is not set)
- true if the result is not 0 (bit is set)
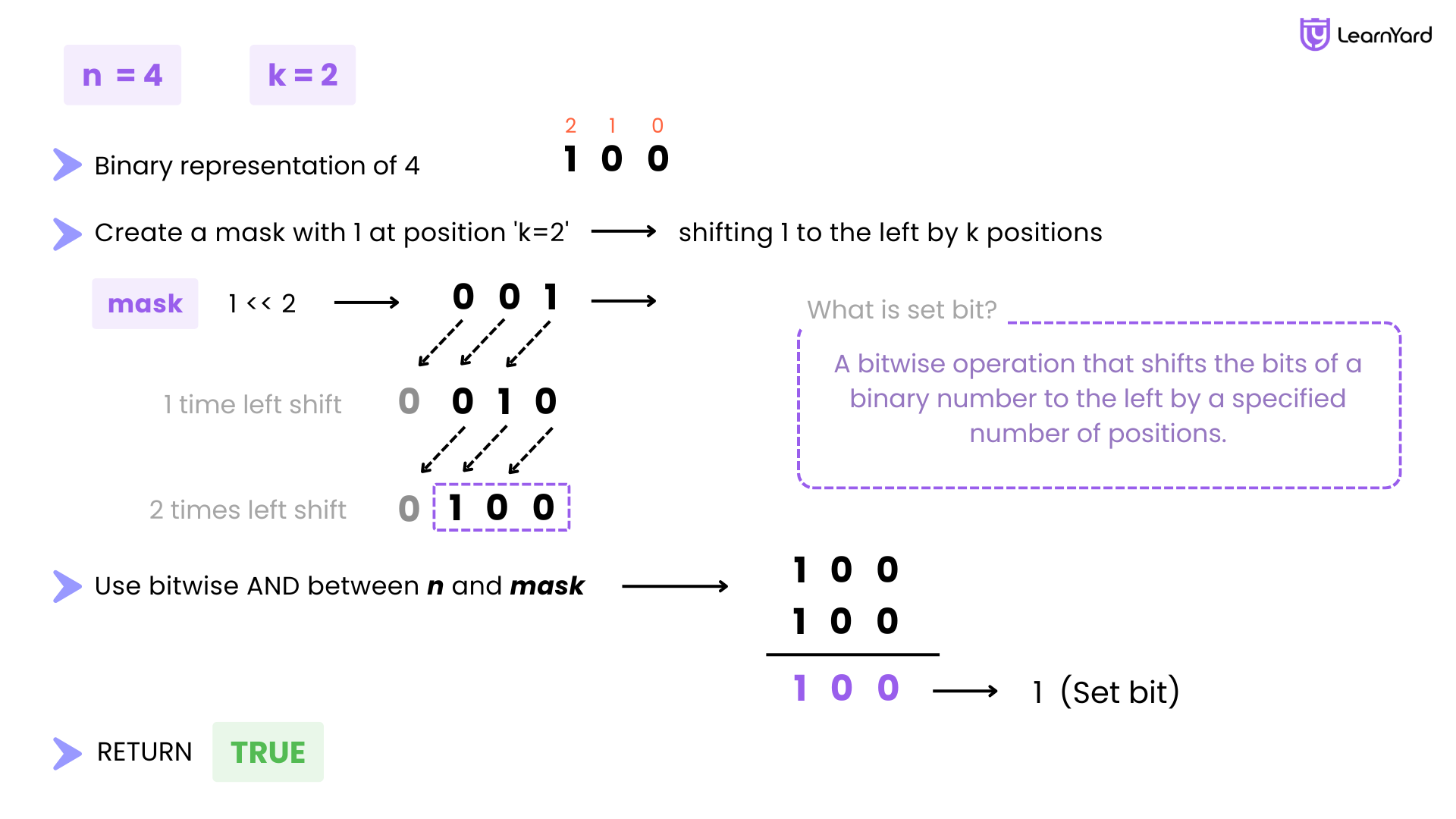
Dry Run
Let's do a detailed Dry Run for the given input to understand how the function checks whether the kth bit is set or not.
Input: n = 4, k = 2
Step 1: Understand the target bit position
We're asked to check the 2nd bit (0-based) of the number 4.
This means we're interested in the third bit from the right in the binary representation.
Step 2: Convert number to binary
Convert 4 to binary:
4 = 100 (in binary)
Now label the bit positions from right to left (0-based indexing):
Position: 2 1 0
Binary : 1 0 0
We can see that the bit at position 2 is 1, which means it is set.
Step 3: Create the mask
We now create a mask to target the 2nd bit:
mask = 1 << k = 1 << 2 = 4
Binary of mask = 100
Step 4: Perform bitwise AND operation
Now we check whether the 2nd bit is set using bitwise AND:
(n & mask) = (4 & 4)
Binary representation:
n = 100
mask = 100
AND = 100 → which is 4
Since the result is not zero, the bit at position 2 is set.
Step 5: Return the result
The function returns true, indicating that the 2nd bit is set.
Final Output: true
Code for All Languages
C++
#include <iostream> // for cin and cout
using namespace std;
class Solution {
public:
// Function to check if the kth bit is set (1) or not
bool checkKthBit(int n, int k) {
// Step 1: Create a mask with 1 at position 'k'
// This is done by shifting 1 to the left by k positions
int mask = 1 << k;
// Step 2: Use bitwise AND between n and mask
// If the result is 0, it means kth bit was 0 (not set)
// Otherwise, the kth bit was 1 (set)
if ((n & mask) == 0) {
return false; // kth bit is not set
} else {
return true; // kth bit is set
}
}
};
// Driver code
int main() {
int n, k;
// Input the number and the bit position (0-based index)
cin >> n >> k;
Solution sol;
// Call the function to check if kth bit is set
bool result = sol.checkKthBit(n, k);
// Output true if set, false otherwise
if (result == true) {
cout << "true" << endl;
} else {
cout << "false" << endl;
}
return 0;
}Java
import java.util.Scanner; // for Scanner class
class Solution {
// Function to check if the kth bit is set (1) or not
static boolean checkKthBit(int n, int k) {
// Step 1: Create a mask with 1 at position 'k'
// This is done by shifting 1 to the left by k positions
int mask = 1 << k;
// Step 2: Use bitwise AND between n and mask
// If the result is 0, it means kth bit was 0 (not set)
// Otherwise, the kth bit was 1 (set)
if ((n & mask) == 0) {
return false; // kth bit is not set
} else {
return true; // kth bit is set
}
}
}
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt(); // Input the number
int k = sc.nextInt(); // Input the bit position (0-based index)
// Call the function to check if kth bit is set
boolean result = Solution.checkKthBit(n, k);
// Output true if set, false otherwise
if (result == true) {
System.out.println("true");
} else {
System.out.println("false");
}
}
}
Python
class Solution:
# Function to check if the kth bit is set (1) or not
def checkKthBit(self, n, k):
# Step 1: Create a mask with 1 at position 'k'
# This is done by shifting 1 to the left by k positions
mask = 1 << k
# Step 2: Use bitwise AND between n and mask
# If the result is 0, it means kth bit was 0 (not set)
# Otherwise, the kth bit was 1 (set)
if (n & mask) == 0:
return False # kth bit is not set
else:
return True # kth bit is set
# Driver code
if __name__ == "__main__":
n, k = map(int, input().split())
sol = Solution()
# Call the function to check if kth bit is set
result = sol.checkKthBit(n, k)
# Output true if set, false otherwise
if result == True:
print("true")
else:
print("false")
Javascript
/**
* @param {Number} n
* @param {Number} k
* @returns {boolean}
*/
class Solution {
checkKthBit(n, k) {
// Step 1: Create a mask with 1 at position 'k'
// This is done by shifting 1 to the left by k positions
let mask = 1 << k;
// Step 2: Use bitwise AND between n and mask
// If the result is 0, it means kth bit was 0 (not set)
// Otherwise, the kth bit was 1 (set)
if ((n & mask) === 0) {
return false; // kth bit is not set
} else {
return true; // kth bit is set
}
}
}
// Driver code
const readline = require('readline');
const rl = readline.createInterface({
input: process.stdin,
output: process.stdout
});
rl.question('', function (input) {
let [n, k] = input.split(' ').map(Number);
const sol = new Solution();
let result = sol.checkKthBit(n, k);
// Output true if set, false otherwise
if (result === true) {
console.log("true");
} else {
console.log("false");
}
rl.close();
});
Time Complexity: O(1)
Bit Manipulation Operations: O(1)
The task involves checking whether the kth bit of a number n is set using basic bitwise operations. These are known to run in constant time, as they directly manipulate bits at the hardware level without any looping or recursion.
Mask Creation: O(1)
We use 1 << k to generate a bitmask with a 1 only at the kth position. The left shift operator is a low-level CPU operation that runs in constant time.
Bitwise AND Check: O(1)
We perform n & mask, which checks whether the kth bit in n is 1 or 0. This is a simple bitwise AND operation and runs in O(1) time.
Conditional Check: O(1)
The result of the bitwise operation is compared with 0 in an if condition. This comparison is a basic boolean check and does not depend on the size of n or k. So, it also executes in O(1) time.
Final Time Complexity: O(1)
Every step — bitmask creation, bitwise AND, comparison, return, and printing — is performed in constant time.
There are no loops, no recursive calls, and no operations that depend on the value or size of n or k.
Hence, the entire function executes in O(1) time.
Space Complexity: O(1)
Auxiliary Space Complexity: O(1)
This refers to the extra space used during the execution of the function, excluding input and output. In this program:
- A few fixed-size integer variables are declared: n, k, mask, and the internal result of the bitwise operation.
- No dynamic memory allocation, arrays, or large data structures are used.
- The function performs all its computation using constant-sized data types.
Hence, the auxiliary space used is constant, i.e., O(1).
Total Space Complexity: O(1)
This includes both the auxiliary space and the space used for input and output. In this program:
- Inputs n and k are simple integer variables.
- No extra storage is required for handling output beyond these fixed-size operations.
- No additional memory is used throughout the program beyond what’s needed for basic variables.
Thus, the total space requirement remains constant, resulting in a total space complexity of O(1).
Similar Problems
Given a 32 bit unsigned integer num and an integer i. Perform following operations on the number -
1. Get i-th bit
2. Set i-th bit
3. Clear i-th bit
Given a non-negative number n. The problem is to set the rightmost unset bit in the binary representation of n.