Jump Game Solution In C++/Java/Python/JS
Problem Description
You are given an integer array nums. You are initially positioned at the array's first index, and each element in the array represents your maximum jump length at that position.
Return true if you can reach the last index, or false otherwise.
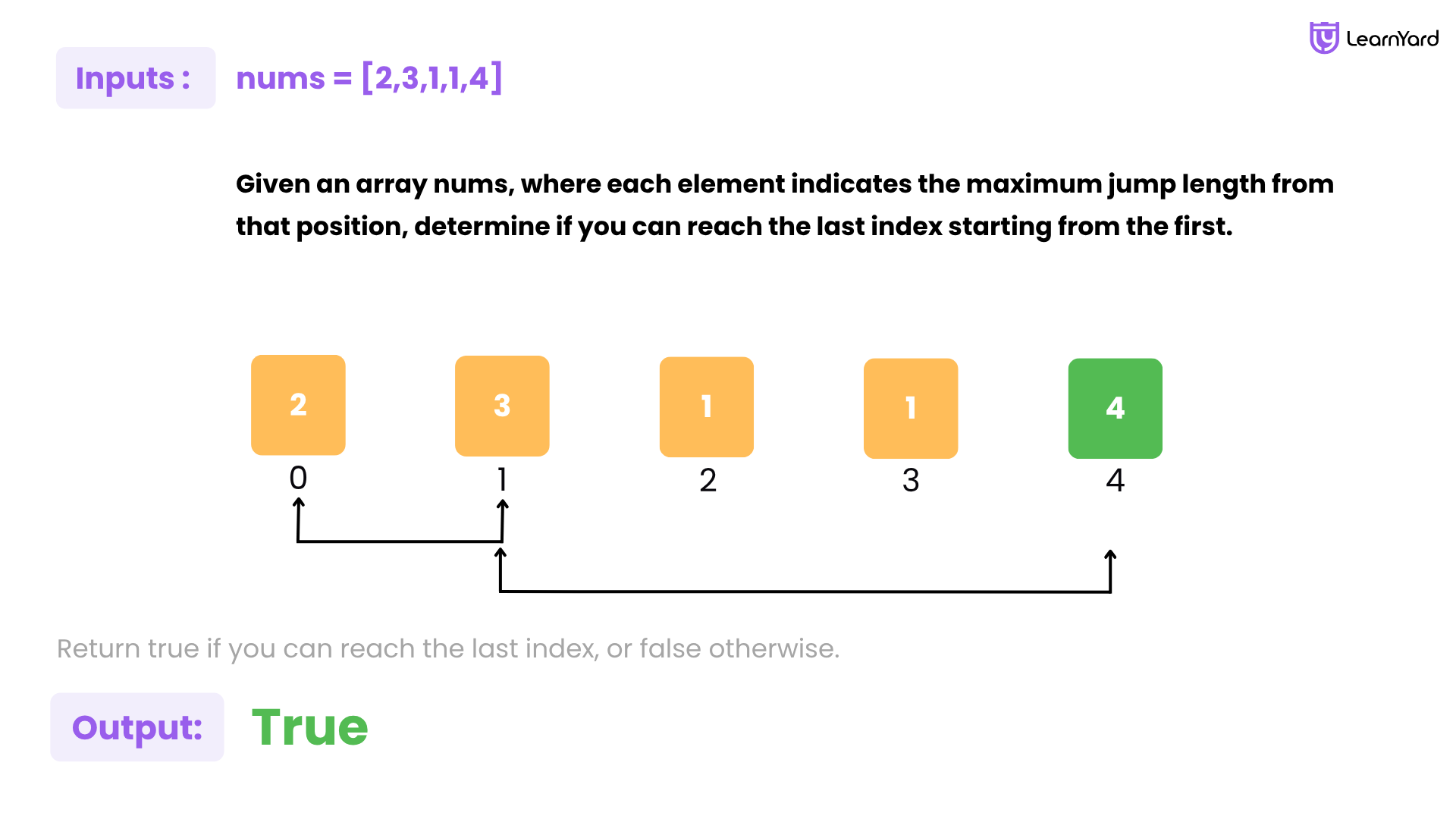
Example
Input: nums = [2,3,1,1,4]
Output: true
Explanation: Jump 1 step from index 0 to 1, then 3 steps to the last index.
Input: nums = [3,2,1,0,4]
Output: false
Explanation: You will always arrive at index 3 no matter what. Its maximum jump length is 0, which makes it impossible to reach the last index.
Constraints
- 1 <= nums.length <= 104
- 0 <= nums[i] <= 105
Figuring out "Jump Game" can be solved using different approaches. We will first figure out the most intuitive approach and move to the optimal approach if exists. Let's sit with a pen and paper and figure out the algorithm !!
Brute Force Approach
Intuition
We are given an array where each element represents the maximum steps we can move forward from that index. Our goal is to determine if we can reach the last index starting from the first index. To do this, we need to check every possible path from each index, exploring all reachable positions, and see if any of them lead to the last index.
Let's understand with an Example: nums = {2, 0, 2, 1, 4}
Exploring All Possible Paths for nums = {2, 0, 2, 1, 4}
Start at Index 0 (value = 2)
Since we have 2 jumps available, we have multiple choices:
- Jump 1 step → Go to index 1
- Jump 2 steps → Go to index 2
Path so far: {0}
From Index 0, Jump 1 Step to Index 1 (value = 0)
From index 1, we cannot jump anywhere since the value is 0. This path fails as we are stuck at index 1.
Path so far: {0 → 1} (Stuck, going back to explore other options from index 0)
So, Path so far: {0}
From Index 0, Jump 2 Steps to Index 2 (value = 2)
From index 2, we can jump up to 2 steps:
- Jump 1 step → Go to index 3
- Jump 2 steps → Go to index 4
Path so far: {0 → 2}
From Index 2, Jump 1 Step to Index 3 (value = 1)
From index 3, we can jump up to 1 step:
- Jump 1 step → Go to index 4
Path so far: {0 → 2 → 3}
From Index 3, Jump 1 More Step to Index 4 (Last Index)
We successfully reached the last index.
Path so far: {0 → 2 → 3 → 4} (Reached Last Index)
Since we found a path that reaches the last index, the answer is true.
We also have a possibility from index 2 as below:
From Index 2, Jump 2 Steps to Index 4 (Last Index)
We successfully reached the last index.
Path so far: {0 → 2 → 4} (Reached Last Index)
Since we found a path that reaches the last index, the answer is true.
Let's now see how our algorithm looks!
Jump Game Algorithm
- We start at index 0 and try to reach the last index.
- We check if the current index is at or beyond the last index; if yes, we return true.
- We try all possible jumps from 1 to nums[index], moving forward.
- We recursively check if any jump allows reaching the last index.
- We return true if we find a valid path; otherwise, we return false.
Approach
1. Start the Process: We begin by calling canReach(nums, 0), starting at index 0.
2. Check If We Reached the Last Index: If the current index is at or beyond the last index (index >= nums.length - 1), we return true.
3. Explore All Possible Jumps: From the current index, we check all possible jumps from 1 to nums[index], trying each forward movement.
4. Recursively Check for a Valid Path: For each jump, we recursively call canReach(nums, index + jump). If any of these calls return true, we immediately return true.
5. Return False If No Path Works: If none of the jumps lead to the last index, we return false, indicating that reaching the end is not possible.
Dry-Run
Example Input : nums = [2, 0, 1, 3, 0, 2]
Output: True
Explanation
Start at index = 0
- nums[0] = 2, meaning we can jump to:
→ index = 1 (jump of 1)
→ index = 2 (jump of 2) - We explore index = 2 first.
Move to index = 2
- nums[2] = 1, meaning we can jump to:
→ index = 3 (jump of 1) - We move to index = 3.
Move to index = 3
- nums[3] = 3, meaning we can jump to:
→ index = 4 (jump of 1)
→ index = 5 (jump of 2) - We explore index = 5 first.
Move to index = 5
- index = 5 is the last index, so we return True.
Recursive Calls Breakdown:
canReach(0) → canReach(2) → canReach(3) → canReach(5) → True
- Since we reached index = 5, all recursive calls return True.
Final Output: True
Jump Game Solution
Now let's checkout the "Jump Game code" in C++, Java, Python and JavaScript.
"Jump Game" Code in all Languages.
1. Jump Game solution in C++ Try on Compiler
class Solution {
public:
// Recursive function to check if we can reach the last index
bool canReach(vector<int>& nums, int index) {
// Base case: If we reach or exceed the last index, return true
if (index >= nums.size() - 1) return true;
// Try all possible jumps from the current position
for (int jump = 1; jump <= nums[index]; jump++) {
// If any jump leads to a solution, return true
if (canReach(nums, index + jump)) {
return true;
}
}
// If no jump works, return false
return false;
}
// Wrapper function to start recursion from index 0
bool canJump(vector<int>& nums) {
return canReach(nums, 0);
}
};2. Jump Game Solution in Java Try on Compiler
class Solution {
// Recursive function to check if we can reach the last index
private boolean canReach(int[] nums, int index) {
// Base case: If we reach or exceed the last index, return true
if (index >= nums.length - 1) return true;
// Try all possible jumps from the current position
for (int jump = 1; jump <= nums[index]; jump++) {
// If any jump leads to a solution, return true
if (canReach(nums, index + jump)) {
return true;
}
}
// If no jump works, return false
return false;
}
// Wrapper function to start recursion from index 0
public boolean canJump(int[] nums) {
return canReach(nums, 0);
}
}3. Jump Game Solution in Python Try on Compiler
class Solution:
# Recursive function to check if we can reach the last index
def canReach(self, nums: List[int], index: int) -> bool:
# Base case: If we reach or exceed the last index, return True
if index >= len(nums) - 1:
return True
# Try all possible jumps from the current position
for jump in range(1, nums[index] + 1):
# If any jump leads to a solution, return True
if self.canReach(nums, index + jump):
return True
# If no jump works, return False
return False
# Wrapper function to start recursion from index 0
def canJump(self, nums: List[int]) -> bool:
return self.canReach(nums, 0)4. Jump Game solution in JavaScript Try on Compiler
/**
* Recursive function to check if we can reach the last index
* @param {number[]} nums
* @param {number} index
* @return {boolean}
*/
function canReach(nums, index) {
// Base case: If we reach or exceed the last index, return true
if (index >= nums.length - 1) return true;
// Try all possible jumps from the current position
for (let jump = 1; jump <= nums[index]; jump++) {
// If any jump leads to a solution, return true
if (canReach(nums, index + jump)) {
return true;
}
}
// If no jump works, return false
return false;
}
/**
* Wrapper function to start recursion from index 0
* @param {number[]} nums
* @return {boolean}
*/
function canJump(nums) {
return canReach(nums, 0);
}
Jump Game Complexity Analysis
Time Complexity: O(2ⁿ)
Recursive Calls:
- From each index i, we make at most nums[i] recursive calls.
- In the worst case, if nums[i] allows n-1 jumps (e.g., nums = [n-1, n-2, ..., 1, 0]), the recursion forms a tree-like structure with a branching factor of nearly n.
- The number of recursive calls can grow exponentially, leading to O(2ⁿ) complexity in the worst case.
Thus, the time complexity is O(2ⁿ) (exponential).
Space Complexity: O(n)
Auxiliary Space for Recursion:
- The recursion depth is at most O(n) (in case of a worst-case scenario where all jumps are 1).
- No additional data structures are used apart from recursive calls.
Thus, the space complexity is O(n) due to recursive stack space.
This brute force approach takes exponential time complexity (O(2ⁿ)), which is highly inefficient. This approach will fail for large inputs. The interviewer will not be satisfied with this, so let's figure out an optimal solution.
Optimal Approach
Intuition
We are given an array nums, where each element tells us the maximum number of steps we can jump forward from that position. Our goal is to determine whether we can reach the last index.
Let's Understand with an example:
nums = [2, 3, 1, 0, 2, 0, 4]
Start at index 0 (Farthest reach = 2, so we can go up to index 2)
Value at index 0 is 2, so we can jump to index 1 or 2.
Farthest reach is now 2.
Move to index 1 (Farthest reach = 2, so we can come here)
Value at index 1 is 3, so we can jump to index 2, 3, or 4.
So, Farthest reach is now 4.
Move to index 2 (Farthest reach = 4, so we can come here)
Value at index 2 is 1, so we can jump to index 3.
Farthest reach remains 4 (since 3 is within 4).
Move to index 3 (Farthest reach = 4, so we can come here)
Value at index 3 is 0, so we cannot jump forward.
Farthest reach remains 4.
Move to index 4 (Farthest reach = 4, so we can come here)
Value at index 4 is 2, so we can jump to index 5 or 6.
So, Farthest reach is now 6 (which is the last index!).
Move to index 5 (Farthest reach = 6, so we can come here)
Value at index 5 is 0, so we cannot jump forward.
Farthest reach remains 6.
Move to index 6 (Farthest reach = 6, so we can come here, and we reached the last index!)
We successfully reached the last index.
Even though we encountered 0s at index 3 and index 5, we were still able to move beyond them because our previous reach extended past them.Since we reached the last index, the answer is true.
Key Observations
- At each step, we check if we are within our farthest known reach.
- If we encounter a 0, we don’t stop as long as we had already calculated a way to go past it.
- We only track the farthest position we can reach, rather than considering every possible jump.
Well summarized! Now, if you think about it, what kind of approach are we using here?
We are making the best possible choice at each step without looking ahead too much. This sounds like a greedy algorithm!
Exactly! The greedy approach works perfectly here because, at each step, we maximize our reach by updating the farthest index we can get to. without needing to explore all possible paths exhaustively.
Jump Game Algorithm
- We initialize reachable = 0 to track the farthest index we can reach.
- We iterate through nums and check if the current index i is within reachable.
- If i goes beyond reachable, we return false since we are stuck.
- We update reachable by extending it to the maximum possible index from i
- If we finish the loop, we return true, as we have successfully reached or passed the last index.
Approach
Initialize Variables
- Define reachable to keep track of the farthest index that can be reached.
- Initially, reachable is set to 0 since the starting position is at index 0.
Iterate Through Each Index
- Use a loop to traverse every index i in nums.
- At each step, check whether movement beyond the current index is possible based on reachable.
Check If Movement Is Blocked
- If the current index i is greater than reachable, then index i is beyond the maximum reach, making further progress impossible.
- In this case, return false immediately, as reaching the last index is not feasible.
Update the Maximum Reach
- If index i is within reachable, calculate the maximum index that can be reached from this position.
- Update reachable to track the farthest possible position that can be reached at any point.
- This ensures that movement continues as long as an extended reach is available.
Return the Result: If the loop completes without encountering an unreachable index, the last index has been reached or surpassed. In this case, return true, indicating that reaching the last index is possible.
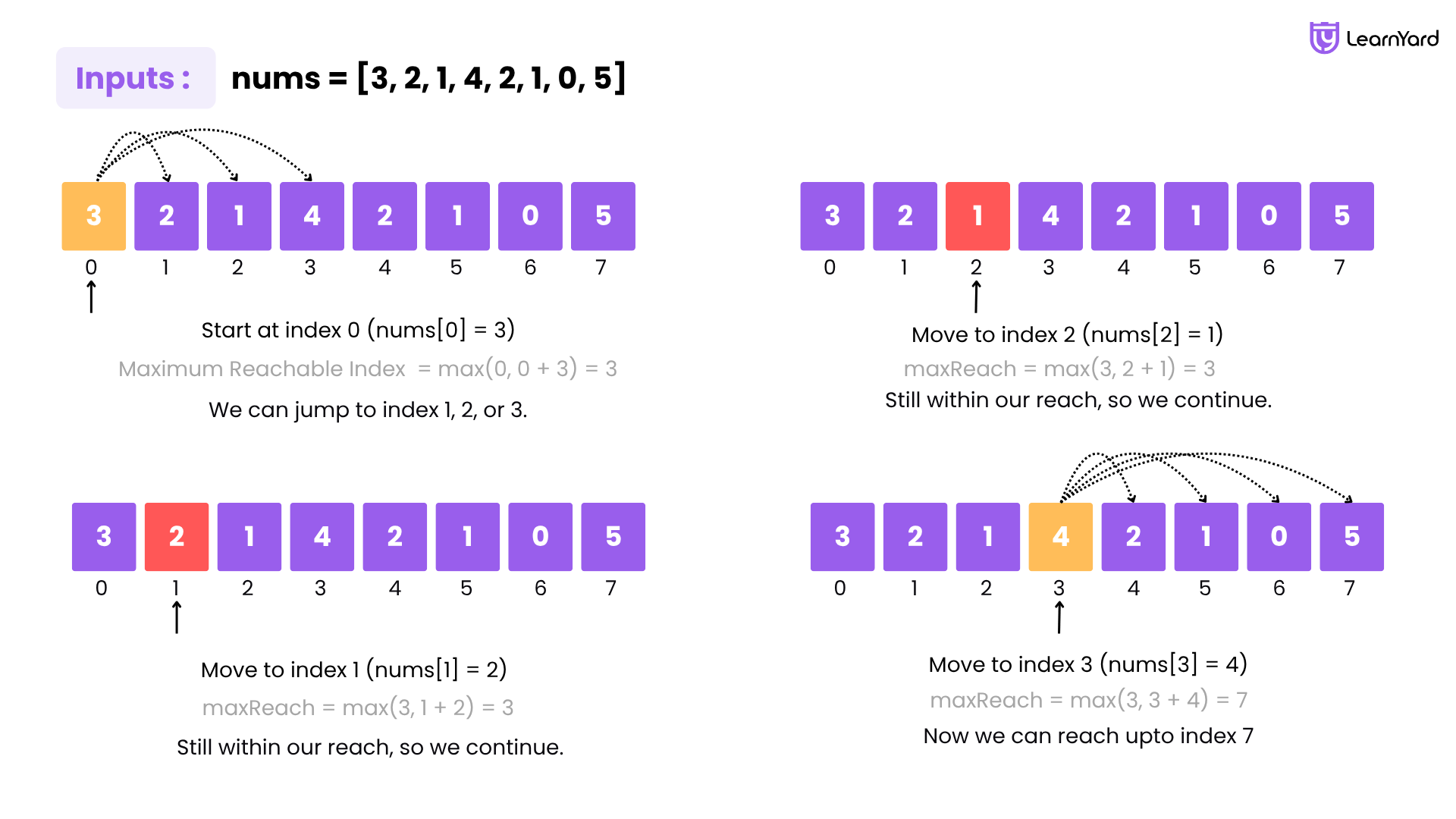
Dry-Run
Example Input: nums = [3, 2, 1, 4, 2, 1, 0, 5]
Output: true
Step-by-Step Dry run:
1. Start at index 0 (nums[0] = 3):
- Maximum Reachable Index (maxReach) = max(0, 0 + 3) = 3
- We can jump to index 1, 2, or 3.
2. Move to index 1 (nums[1] = 2):
- maxReach = max(3, 1 + 2) = 3
- Still within our reach, so we continue.
3. Move to index 2 (nums[2] = 1):
- maxReach = max(3, 2 + 1) = 3
- Still within our reach, so we continue.
4. Move to index 3 (nums[3] = 4):
- maxReach = max(3, 3 + 4) = 7
- Now we can reach index 7!
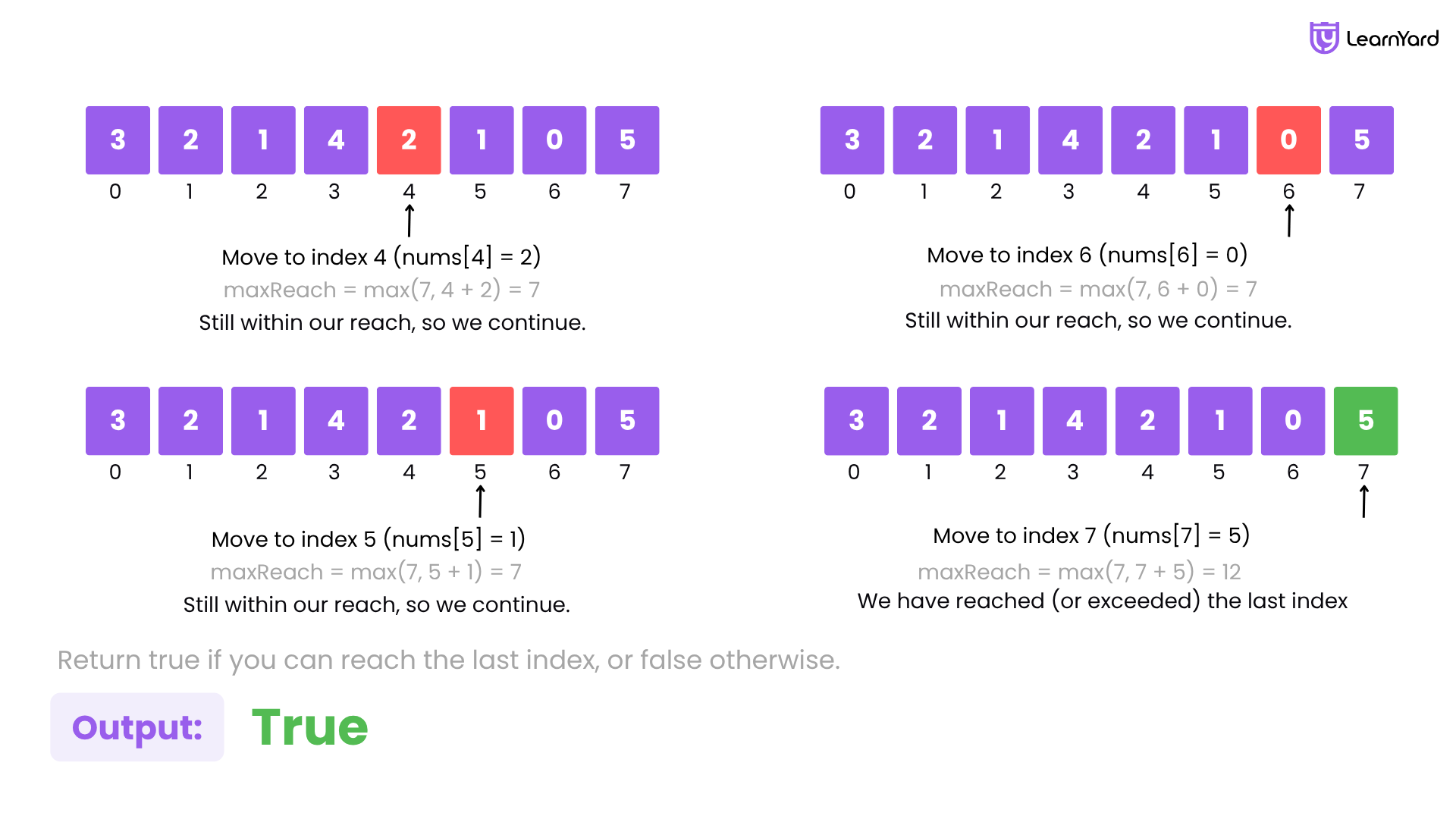
5. Move to index 4 (nums[4] = 2):
- maxReach = max(7, 4 + 2) = 7
- Still within reach, so we continue.
6. Move to index 5 (nums[5] = 1):
- maxReach = max(7, 5 + 1) = 7
- Still within reach, so we continue.
7. Move to index 6 (nums[6] = 0):
- maxReach = max(7, 6 + 0) = 7
- Still within reach, so we continue.
8. Move to index 7 (nums[7] = 5):
- maxReach = max(7, 7 + 5) = 12
- We have reached (or exceeded) the last index!
Final Answer: true
Jump Game Solution
Now let's checkout the "Jump Game code" in C++, Java, Python and JavaScript.
"Jump Game" Code in all Languages.
1. Jump Game solution in C++ Try on Compiler
class Solution {
public:
// Function to check if we can reach the last index
bool canJump(vector<int>& nums) {
// Variable to store the maximum index we can reach
int maxReach = 0;
// Traverse the array
for (int i = 0; i < nums.size(); i++) {
// If our current index exceeds the maximum reachable index, return false
if (i > maxReach) return false;
// Update maxReach by considering the jump from the current index
maxReach = max(maxReach, i + nums[i]);
}
// If we complete the loop, we can reach the last index
return true;
}
};
2. Jump Game Solution in Java Try on Compiler
class Solution {
public boolean canJump(int[] nums) {
// Variable to store the maximum index we can reach
int maxReach = 0;
// Traverse the array
for (int i = 0; i < nums.length; i++) {
// If our current index exceeds the maximum reachable index, return false
if (i > maxReach) return false;
// Update maxReach by considering the jump from the current index
maxReach = Math.max(maxReach, i + nums[i]);
}
// If we complete the loop, we can reach the last index
return true;
}
}3. Jump Game Solution in Python Try on Compiler
class Solution:
# Function to check if we can reach the last index
def canJump(self, nums: List[int]) -> bool:
# Variable to store the maximum index we can reach
maxReach = 0
# Traverse the array
for i in range(len(nums)):
# If our current index exceeds the maximum reachable index, return False
if i > maxReach:
return False
# Update maxReach by considering the jump from the current index
maxReach = max(maxReach, i + nums[i])
# If we complete the loop, we can reach the last index
return True4. Jump Game solution in JavaScript Try on Compiler
/**
* @param {number[]} nums
* @return {boolean}
*/
var canJump = function(nums) {
// Variable to store the maximum index we can reach
let maxReach = 0;
// Traverse the array
for (let i = 0; i < nums.length; i++) {
// If our current index exceeds the maximum reachable index, return false
if (i > maxReach) return false;
// Update maxReach by considering the jump from the current index
maxReach = Math.max(maxReach, i + nums[i]);
}
// If we complete the loop, we can reach the last index
return true;
};Jump Game Complexity Analysis
Time Complexity: O(n)
Iterating through the array while maintaining maxReach:
- We traverse the array once, updating maxReach at each step.
- This operation takes O(n) time.
Checking if we can reach the last index:
- Each index is processed in constant time.
- This takes O(1) time.
Thus, the total time complexity is, O(n)+O(1) = O(n)
Space Complexity: O(1)
Space Complexity Analysis:
Auxiliary Space Complexity:
- The algorithm only uses one extra variable (maxReach).
- No additional data structures are used.
- Thus, auxiliary space complexity is O(1).
Total Space Complexity:
- Input storage (array of size n): O(n)
- In-place iteration → No extra space
- Variables (constant space) → O(1)
Thus, the total space complexity is O(1)
Similar Problems
You are given a 0-indexed array of integers nums of length n. You are initially positioned at nums[0].
Each element nums[i] represents the maximum length of a forward jump from index i. In other words, if you are at nums[i], you can jump to any nums[i + j] where:
- 0 <= j <= nums[i] and
- i + j < n
Return the minimum number of jumps to reach nums[n - 1]. The test cases are generated such that you can reach nums[n - 1].
Given an array of non-negative integers arr, you are initially positioned at start index of the array. When you are at index i, you can jump to i + arr[i] or i - arr[i], check if you can reach any index with value 0.
Notice that you can not jump outside of the array at any time.