Get, Set, Clear ith Bit Solution In C++/Java/Python/JS
Problem Description
Given a 32 bit unsigned integer num and an integer i. Perform following operations on the number -
1. Get i-th bit
2. Set i-th bit
3. Clear i-th bit
Note : For better understanding, we are starting bits from 1 instead 0. (1-based). You have to print space three space separated values ( as shown in output without a line break) and do not have to return anything.
What is meant by Get, Set and Clear?
What is the i-th bit?
Every number in binary is made up of bits (0s and 1s). These bits are like positions in a list:
- The rightmost bit is the 1st bit (Least Significant Bit or LSB),
- The next is the 2nd bit, and so on until the 32nd bit (since it's a 32-bit number).
Example:
Take the number 70. In binary, it is 1000110. From right to left, the bits are:
- Bit-1 = 0
- Bit-2 = 1
- Bit-3 = 1
- Bit-4 = 0
- Bit-5 = 0
- Bit-6 = 0
- Bit-7 = 1
So the 3rd bit (from the right) is 1.
- Get the i-th Bit
This means: "Tell me whether the i-th bit is 1 or 0?" - Set the i-th Bit
This means: "Make the i-th bit to become 1, even if it was 0." - Clear the i-th Bit
This means: "Make the i-th bit to become 0, even if it was 1."
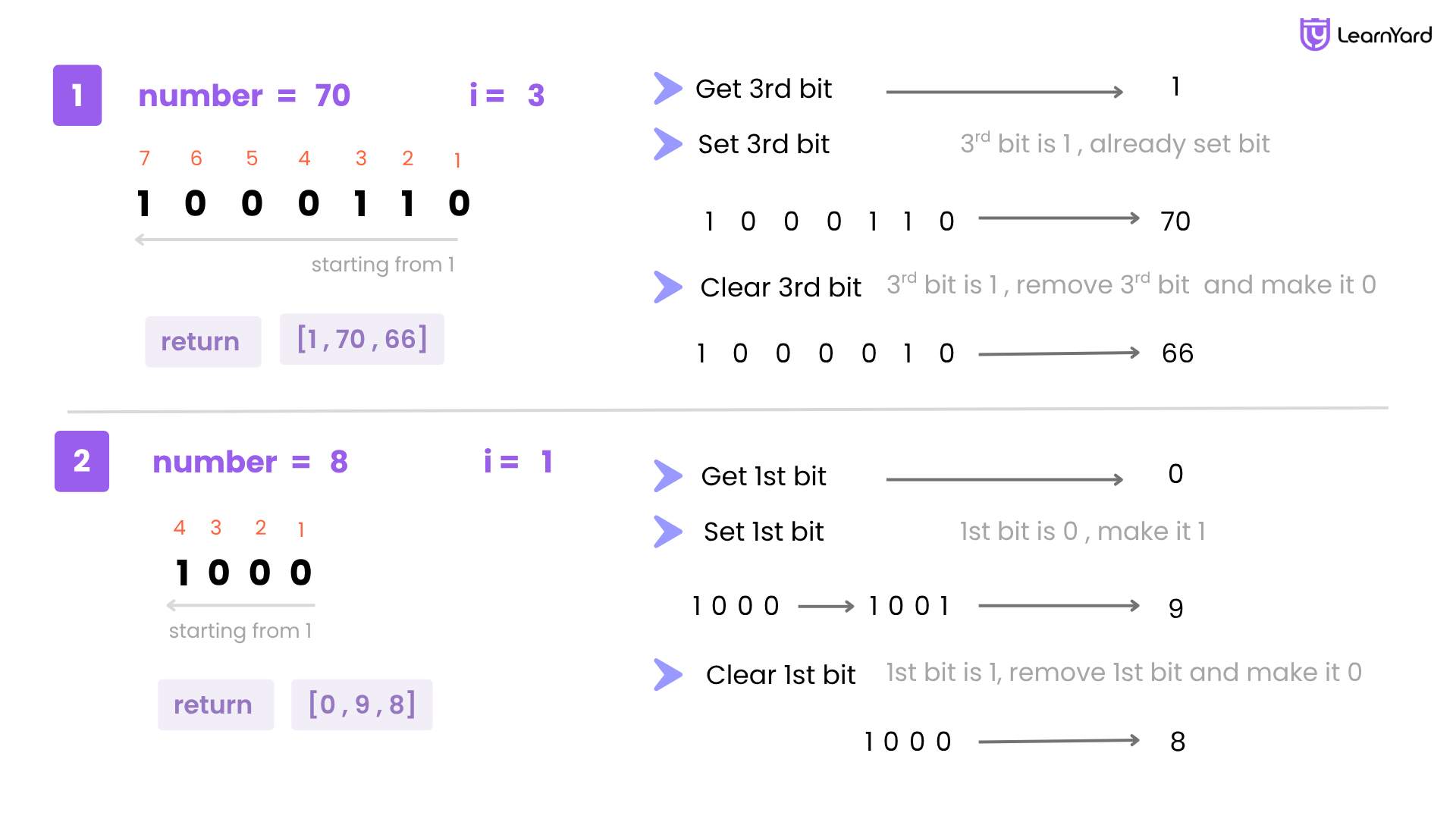
Example
Input: num = 70, i = 3
Output: 1 70 66
Explanation: Bit at the 3rd position from LSB is 1. (1 0 0 0 1 1 0) .The value of the given number after setting the 3rd bit is 70. The value of the given number after clearing 3rd bit is 66. (1 0 0 0 0 1 0)
Input: num = 8, i = 1
Output: 0 9 8
Explanation: Bit at the first position from LSB is 0. (1 0 0 0). The value of the given number after setting the 1st bit is 9. (1 0 0 1). The value of the given number after clearing 1st bit is 8. (1 0 0 0)
Constraints
- 1 <= num <= 10^9
- 1<= i <=32
Think of a number as a sequence of bits lined up, each one holding a small but critical piece of information. Now imagine if we had direct control to read, modify, or even reset any specific bit—how powerful would that be while working at the lowest level of data?
Optimal Approach
Intuition
Let’s start with the basic observation — when we deal with any number in computers, it is internally stored as a sequence of bits (0s and 1s). Each bit holds a power of 2, and by turning specific bits on (1) or off (0), the number holds its value. So, if we want to perform specific operations like getting, setting, or clearing a bit at a particular position, we need to directly interact with those individual bits using bitwise operators. And that’s exactly what this problem is about — it’s not about converting to binary and counting bits manually, but learning how to access, modify, or reset bits efficiently using logic.
Now let’s build some intuition. Say we’re given a number like 70, and we’re asked to check or modify its 3rd bit (from the right). First thing to note — the input gives us the position in 1-based indexing, but computers work in 0-based indexing, so we subtract 1. Once we know the right position, we want to point a finger directly to that bit — that’s where bitmasking comes in. We create a mask using 1 shifted to the left by our target position, so that only that bit is set. For example, 1 << 2 gives 00000100, meaning only the 3rd bit is 1.
What is mask and Left Shift (<<) Operator?
A mask is simply a number that helps us focus on specific bits within another number. Think of it like using a stencil when painting — the stencil (mask) allows us to paint only in specific areas and ignore the rest. Similarly, in programming, a bitmask helps us isolate, set, or clear particular bits in a number.
But the mask has to be smartly constructed — it should have a 1 only at the position we care about and 0 everywhere else.
For example, if we want to work with the 3rd bit (from the right), we make a mask like this:
00000100 (which is 4 in decimal) — this has 1 only at the 3rd position and zeroes elsewhere.
This kind of mask helps us target the 3rd bit only, without disturbing others.
What is the Left Shift (<<) Operator?
The Left Shift (<<) operator is how we create such masks or shift bits to the left.
Here’s what happens when we do something like:
1 << 3
Let’s understand this step-by-step:
- Start with the number 1 → in binary: 00000001
- Shift it 3 positions to the left → becomes 00001000
- This is now 8 in decimal.
So, doing 1 << i creates a number where only the i-th bit is 1 and the rest are 0s.
That’s exactly what we want in a mask when we want to work with the i-th bit.
Now we use this mask cleverly:
- To get the bit, we use AND. If that bit is 1, the result will be non-zero.
Detailed Explanation
We create a mask where only the i-th bit is 1, and the rest are 0, using 1 << i.
Then we use bitwise AND (&) with the original number.
If the result is non-zero, it means the bit was 1.
If the result is zero, it means the bit was 0.
Example:
Let’s say our number is 13, and we want to check the 2nd bit (i = 2).
- Binary of 13: 1101
- Mask: 1 << 2 = 0100 (which is 4)
- Now do: 1101 & 0100 = 0100 (which is 4, non-zero)
So, the 2nd bit is set (it's 1).
- To set the bit, we use OR, which will turn it to 1 no matter what.
Detailed Explanation
We again create a mask using 1 << i, and use bitwise OR (|) with the original number.
Why OR?
Because anything OR 1 = 1, and anything OR 0 = original.
So, only the i-th bit changes — rest stay the same.
Example:
Let’s take 9, and we want to set the 1st bit (i = 1).
- Binary of 9: 1001
- Mask: 1 << 1 = 0010 (which is 2)
- Now do: 1001 | 0010 = 1011 (which is 11)
So, we’ve turned ON the 1st bit.
- To clear the bit, we invert the mask and use AND, which turns only that bit off and keeps the rest intact.
Detailed Explanation
We again make the mask 1 << i, but we invert it (~mask) to get 0 at the i-th position and 1s elsewhere.
Then we use bitwise AND (&).
Why AND with ~mask?
Because:
- 1 & 1 = 1
- 1 & 0 = 0
So, only the i-th bit becomes 0, the rest remain untouched.
Example:
Let’s take 13, and we want to clear the 2nd bit (i = 2).
- Binary of 13: 1101
- Mask: 1 << 2 = 0100
- Inverted mask: ~0100 = 1011
- Now do: 1101 & 1011 = 1001 (which is 9)
So, the 2nd bit is now cleared (set to 0).
Approach
Step 1: Convert 1-based Index to 0-based Index
In most programming languages, bit positions are counted from 0 (rightmost bit).
Since the input uses 1-based indexing, we convert it by doing:
pos = i - 1
Step 2: Create a Bit Mask
To target the ith bit, we need to shift 1 to the left by pos positions:
mask = 1 << pos
This places a 1 exactly at the bit position we want to work with.
Step 3: Get the ith Bit
To check whether the ith bit is 1 or 0, we use the bitwise AND:
num & mask
- If result is 0, the bit is not set → getBit = 0
- Otherwise, the bit is set → getBit = 1
We use an if-else condition to assign the result to getBit.
Step 4: Set the ith Bit
To set a particular bit means to make sure that bit is 1, regardless of its current state. To make sure the ith bit is set to 1, we use the bitwise OR:
setBit = num | mask
This operation sets the desired bit without affecting the others.
Step 5: Clear the ith Bit
Clearing a bit means setting it to 0, regardless of its current state.
To do this, we first invert the mask using bitwise NOT. Basically, we take the bitwise NOT of the mask:
~mask
Then perform:
clearBit = num & (~mask)
This clears the targeted bit while keeping other bits unchanged.
Step 6: Output the Results
After calculating getBit, setBit, and clearBit, we print these values separated by spaces.
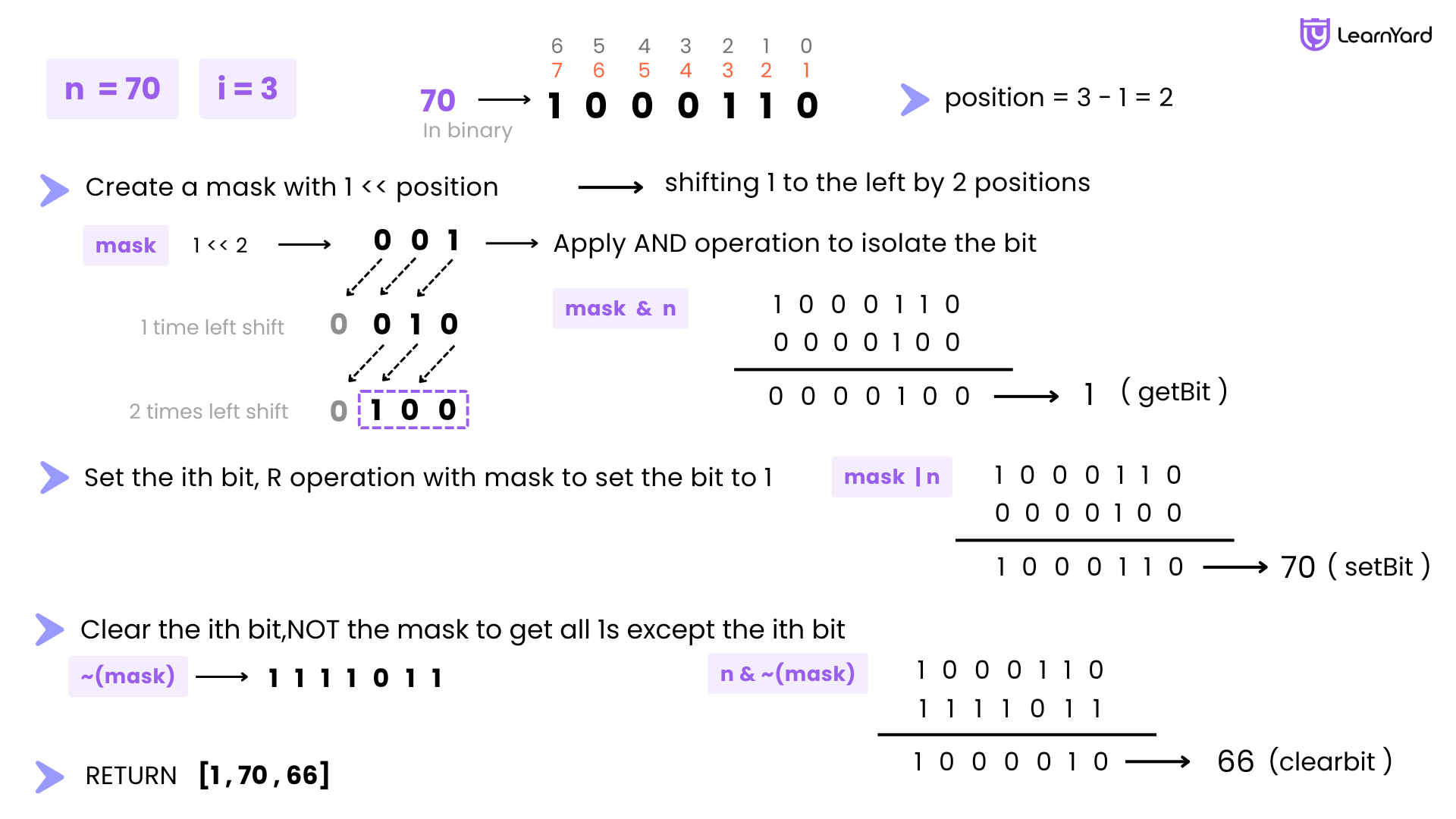
Dry Run
Let's do a detailed Dry Run for the given input to understand how the function performs bit manipulation: Input: num = 70, i = 3
Step 1: Convert 1-based index to 0-based
We subtract 1 from i to get the position:
pos = i - 1 = 3 - 1 = 2
This means we are interested in the 2nd bit (0-based) of the number.
Step 2: Convert number to binary
Let’s convert 70 to binary:
70 = 1000110 (in binary)
Now we focus on the 2nd bit from the right (0-based), which is the third bit from the right in 1-based indexing.
So, the bit positions (0-based from right to left) are:
Position: 6 5 4 3 2 1 0
Binary: 1 0 0 0 1 1 0
Bit at position 2 = 1
Step 3: Create a mask
We now create a mask to isolate or modify the bit at position 2:
mask = 1 << 2 = 4, which is:
mask = 0000100 (binary)
Step 4: Get the ith bit
We perform:
getBit = (num & mask)
= 70 & 4
= 1000110 & 0000100
= 0000100 → which is 4
Since this is not 0, we assign:
getBit = 1
Step 5: Set the ith bit
We perform:
setBit = num | mask
= 70 | 4
= 1000110 | 0000100
= 1000110 → which is still 70
So, setBit = 70
Step 6: Clear the ith bit
We first compute:
~mask = ~(0000100) = 1111011
Now perform:
clearBit = num & (~mask)
= 70 & (~4)
= 1000110 & 1111011
= 1000010 → which is 66
So, clearBit = 66
Final Output
We print the values:
getBit = 1, setBit = 70, clearBit = 66
Final Result: 1 70 66
This means:
- The 3rd bit (1-based) is 1
- Setting it doesn't change the number (already 1) → 70
- Clearing it turns that bit to 0 → 66
Code for All Languages
C++
#include <iostream> // for cin and cout
using namespace std;
class Solution {
public:
// Function to perform get, set, and clear operations on the ith bit
void bitManipulation(int num, int i) {
// Convert 1-based index to 0-based index
int pos = i - 1;
// Step 1: Get the ith bit
// Create a mask with 1 at position 'pos'
int mask = 1 << pos;
// Apply AND operation to isolate the bit
int getBit;
if ((num & mask) == 0) {
getBit = 0;
} else {
getBit = 1;
}
// Step 2: Set the ith bit
// OR operation with mask to set the bit to 1
int setBit = num | mask;
// Step 3: Clear the ith bit
// NOT the mask to get all 1s except the ith bit
// AND operation to clear the bit
int clearBit = num & (~mask);
// Output the results: getBit, setBit, and clearBit
cout << getBit << " " << setBit << " " << clearBit;
}
};
// Driver code
int main() {
int num, i;
// Input the number and the position of bit (1-based index)
cin >> num >> i;
Solution sol;
// Call the function to perform bit manipulation
sol.bitManipulation(num, i);
return 0;
}Java
import java.util.Scanner; // for Scanner class
class Solution {
// Function to perform get, set, and clear operations on the ith bit
static void bitManipulation(int num, int i) {
// Convert 1-based index to 0-based index
int pos = i - 1;
// Step 1: Get the ith bit
// Create a mask with 1 at position 'pos'
int mask = 1 << pos;
// Apply AND operation to isolate the bit
int getBit;
if ((num & mask) == 0) {
getBit = 0;
} else {
getBit = 1;
}
// Step 2: Set the ith bit
// OR operation with mask to set the bit to 1
int setBit = num | mask;
// Step 3: Clear the ith bit
// NOT the mask to get all 1s except the ith bit
// AND operation to clear the bit
int clearBit = num & (~mask);
// Output the results: getBit, setBit, and clearBit
System.out.print(getBit + " " + setBit + " " + clearBit);
}
}
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int num = sc.nextInt();
int i = sc.nextInt();
// Create object and call the function
Solution.bitManipulation(num, i);
}
}Python
# Function to perform get, set, and clear operations on the ith bit
class Solution:
def bitManipulation(self, num, i):
# Convert 1-based index to 0-based index
pos = i - 1
# Step 1: Get the ith bit
# Create a mask with 1 at position 'pos'
mask = 1 << pos
# Apply AND operation to isolate the bit
if (num & mask) == 0:
getBit = 0
else:
getBit = 1
# Step 2: Set the ith bit
# OR operation with mask to set the bit to 1
setBit = num | mask
# Step 3: Clear the ith bit
# NOT the mask to get all 1s except the ith bit
# AND operation to clear the bit
clearBit = num & (~mask)
# Output the results: getBit, setBit, and clearBit
print(getBit, setBit, clearBit)
# Driver code
if __name__ == "__main__":
num, i = map(int, input().split())
sol = Solution()
# Call the function to perform bit manipulation
sol.bitManipulation(num, i)Javascript
class Solution {
// Function to perform get, set, and clear operations on the ith bit
bitManipulation(num, i) {
// Convert 1-based index to 0-based index
const pos = i - 1;
// Step 1: Get the ith bit
// Create a mask with 1 at position 'pos'
const mask = 1 << pos;
// Apply AND operation to isolate the bit
let getBit;
if ((num & mask) === 0) {
getBit = 0;
} else {
getBit = 1;
}
// Step 2: Set the ith bit
// OR operation with mask to set the bit to 1
const setBit = num | mask;
// Step 3: Clear the ith bit
// NOT the mask to get all 1s except the ith bit
// AND operation to clear the bit
const clearBit = num & (~mask);
// Output the results: getBit, setBit, and clearBit
console.log(getBit + " " + setBit + " " + clearBit);
}
}
// Driver code
const readline = require('readline');
const rl = readline.createInterface({
input: process.stdin,
output: process.stdout
});
rl.question('', function(line) {
const [numStr, iStr] = line.trim().split(' ');
const num = parseInt(numStr);
const i = parseInt(iStr);
const sol = new Solution();
// Call the function to perform bit manipulation
sol.bitManipulation(num, i);
rl.close();
});Time Complexity: O(1)
Bit Manipulation Operations: O(1)
The operations for getting, setting, and clearing a bit use bitwise operators (AND, OR, NOT, SHIFT). Each of these executes in constant time regardless of the value of num or i.
Get Bit Operation: O(1)
- We use 1 << pos to create a mask, which is a constant-time shift operation.
- Then we perform num & mask, which is a bitwise AND — a constant-time operation.
- The result is compared with 0 using an
ifcondition — this is a basic comparison, also done in O(1).
So, getting the bit is done in O(1).
Set Bit Operation: O(1)
- We again use 1 << pos to create the mask.
- num | mask is a bitwise OR that modifies only the targeted bit — constant time.
No iteration or recursion is involved. Hence, setting the bit is O(1).
Clear Bit Operation: O(1)
- ~mask flips all bits — this is a constant-time bitwise NOT operation.
- num & (~mask) clears the specific bit using AND, another O(1) operation.
Clearing a bit also takes constant time.
Output Operation: O(1)
- cout prints three integer values with spaces. This involves constant-time formatting and I/O operations for small fixed-size integers.
Final Time Complexity: O(1)
All steps — mask generation, bitwise operations, comparisons, and output — are done in constant time.
There are no loops, no recursion, and no data structures that depend on input size.
Thus, the entire function runs in O(1) time.
Space Complexity: O(1)
Auxiliary Space Complexity: O(1)
This refers to the extra space used internally during the computation, excluding the input and output. In this program:
- Few fixed-size variables are declared: pos, mask, getBit, setBit, and clearBit.
- All of these are simple integer variables. No arrays, objects, strings, or dynamic memory allocations are used.
Hence, the auxiliary space required is constant, i.e., O(1).
Total Space Complexity: O(1)
This includes both the auxiliary space and space used for input/output handling. In this program:
- Input variables num and i are fixed-size integers.
- Output is handled directly using cout, which prints three integers, all of fixed size.
- No additional memory is allocated for storing the output.
- The entire program operates using a constant number of fixed-size variables.
Therefore, the total space required remains constant and is O(1).
Similar Problems
Given two positive integer n and k, check if the kth index bit of n is set or not.
Note: A bit is called set if it is 1.
Given a non-negative number n. The problem is to set the rightmost unset bit in the binary representation of n.