Frequency of the Most Frequent Element Solution In C++/Java/Python/JS
Problem Description:
The frequency of an element is the number of times it occurs in an array.
You are given an integer array nums and an integer k. In one operation, you can choose an index of nums and increment the element at that index by 1.
Return the maximum possible frequency of an element after performing at most k operations.
Examples:
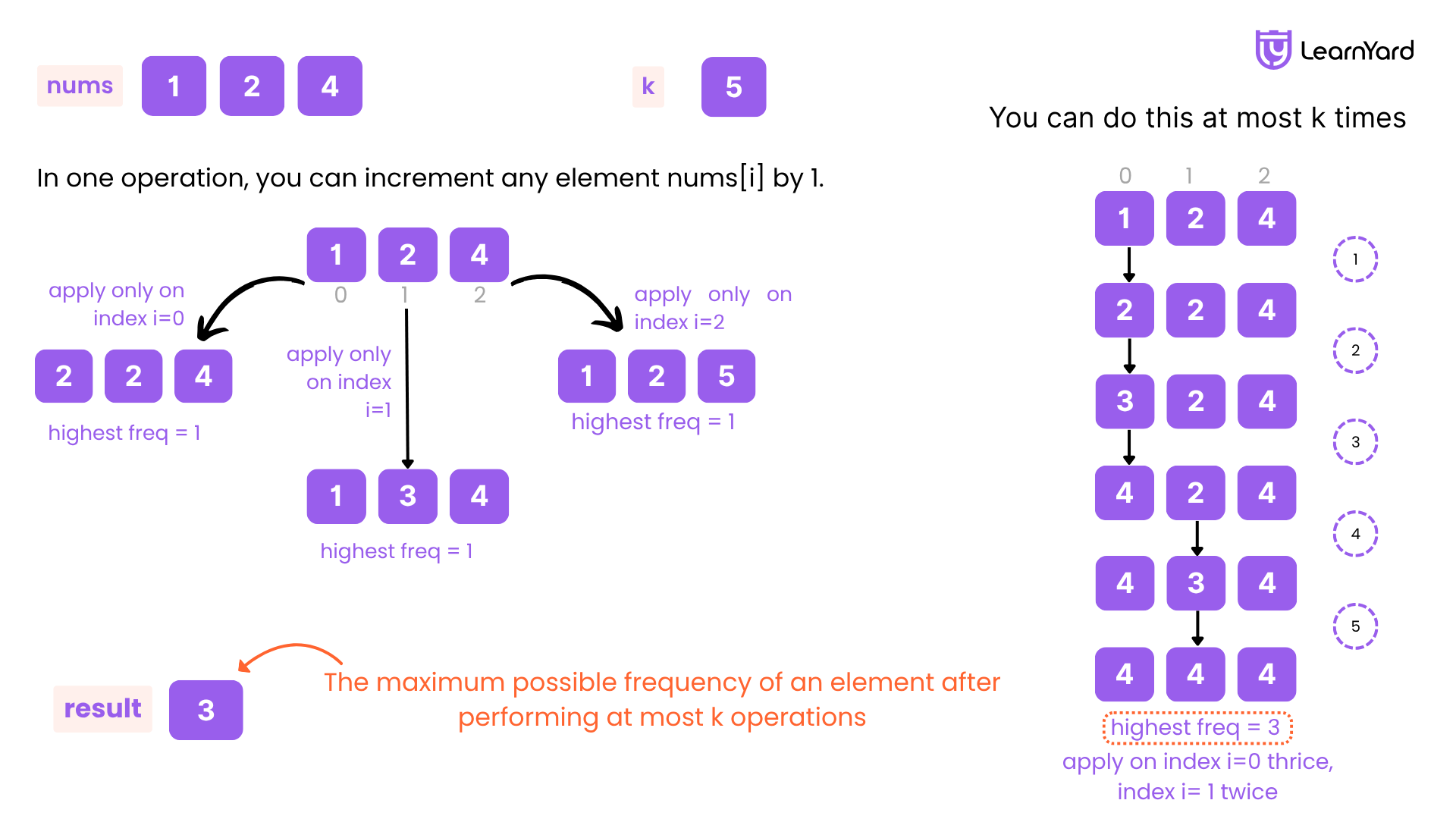
Input: nums = [1,2,4], k = 5
Output: 3
Explanation: Increment the first element three times and the second element two times to make nums = [4,4,4].
4 has a frequency of 3.
Input: nums = [1,4,8,13], k = 5
Output: 2
Explanation: There are multiple optimal solutions:
- Increment the first element three times to make nums = [4,4,8,13]. 4 has a frequency of 2.
- Increment the second element four times to make nums = [1,8,8,13]. 8 has a frequency of 2.
- Increment the third element five times to make nums = [1,4,13,13]. 13 has a frequency of 2.
Input: nums = [3,9,6], k = 2
Output: 1
Constraints:
- 1 <= nums.length <= 105
- 1 <= nums[i] <= 105
- 1 <= k <= 105
To put the problem in simpler terms, we want to make as many elements in the array equal to one particular value as possible, using at most k total increments across any elements. The output should be the highest number of times any single element can appear in the modified array.
Note : We need to output the maximum frequency any element can achieve after performing at most k operations. Not the element which can achieve the maximum frequency.
Brute Force Approach
Intuition:
The first important observation is that the element we want to maximize the frequency of must already exist in the nums array. Why?
Because if we choose an element that’s not present in the array, we would first need to create it using operations, starting from other values, which is inefficient.
On the other hand, if we pick an element that already exists in nums, it automatically starts with a frequency of at least 1 (due to its presence), and we can use our available operations to increment other elements and convert them into this chosen value.
This insight allows us to simplify the problem:
For every element in nums, try to increase the frequency of that specific element as much as possible using at most k operations.
How to efficiently perform k operations to maximise the frequency of nums[i] ?
To solve this subproblem, visualise that in each operation, we can only increment an element by 1; we cannot decrease any number. This gives rise to a critical observation:
Any number greater than our target nums[i] is useless for our purpose, we can't decrease it to match nums[i], so we can safely ignore such numbers when trying to increase the frequency of nums[i].
Instead, we should focus on numbers that are less than or equal to nums[i]. Among these, the ones smaller than nums[i] are our main candidates we can try to increment them to match nums[i], thereby increasing its frequency.
Why Sorting Helps?
To simplify this process, it's helpful to sort the array in ascending order. This ensures that for any element nums[i], all potential candidates (i.e., numbers less than or equal to nums[i]) lie to its left in the array.
This makes it much easier to determine which elements we can increment and how many operations are required.
Now comes an efficiency trick.
To make the most of our k operations, we should first consider converting the largest values among those less than nums[i]. Why?
Because the difference between these values and nums[i] will be smaller, meaning it will cost fewer operations to turn them into nums[i].
So, for a sorted array:
- Start at index i, which is our current target number.
- Look leftward, and try to convert nums[i-1], then nums[i-2], and so on, as long as we have operations left.
- For each element, compute the cost to increment it to nums[i], and subtract this from k.
- Keep track of how many elements we’re able to convert, which gives us the frequency of nums[i].
This greedy approach ensures that we're always choosing the most cost-effective numbers to upgrade, helping us maximise the frequency of our target number using at most k operations.
Once we've implemented the strategy to maximise the frequency of each element nums[i] by incrementing smaller elements using at most k operations, the last step is straightforward.
For every index i in the sorted array, we simulate how many elements we can convert to nums[i] (including itself) using the available operations. This gives us the maximum frequency that nums[i] can achieve.
We store this frequency in a variable, say ans and keep updating it as we move through the array. The goal is to maintain the highest frequency encountered so far.
At the end of this process, ans will contain the maximum frequency achievable for any element in the array after performing at most k operations.
This final value is our answer.
Frequency of the Most Frequent Element Algorithm
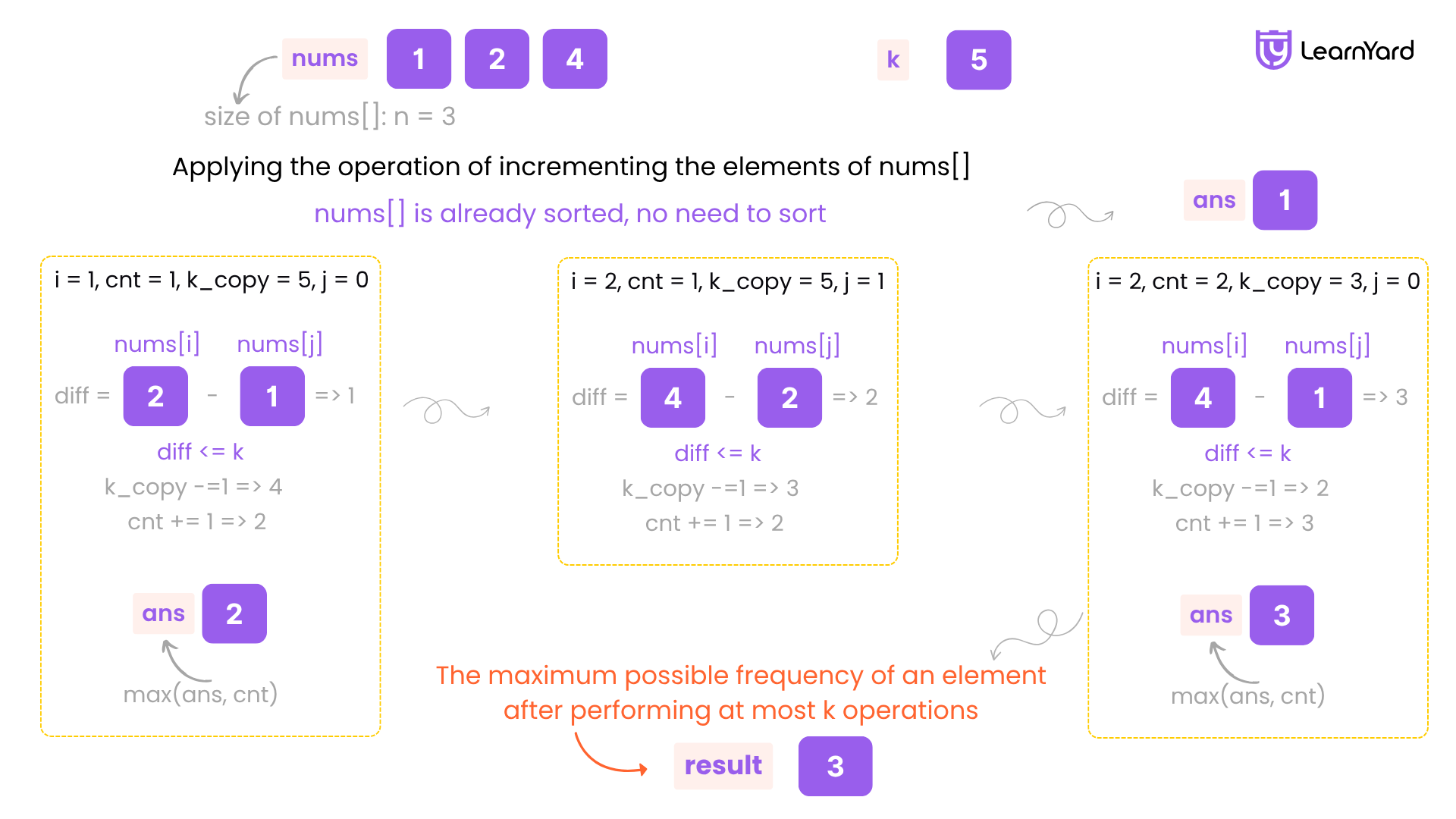
Step 1: Initialisation
- Get the size of the input array to control your loops later.
- Sort the array in non-decreasing order to make it easier to increment smaller elements toward a target value.
- Initialize a variable to keep track of the maximum frequency encountered so far. Start with 1 since a single element is always valid.
Step 2: Loop Through Each Element (Outer Loop)
- Start a loop from the second element (index 1) to the end of the array.
- The idea is to consider each element as a potential target value that you want to make other values equal to, using at most k operations.
Step 3: Try Matching Previous Elements (Inner Loop)
- For the current element (your target), start another loop that goes backwards through all previous elements.
- You want to see how many of those earlier elements can be increased to match the current target.
- Use a copy of k (say, k_copy) to keep track of how many increment operations are still available.
Step 4: Check and Apply Operations
- For each previous element:
- Calculate the cost to increase it to the current target.
- If the cost is less than or equal to the remaining k_copy, include it:
- Deduct the cost from k_copy.
- Increase your match count.
- If the cost is greater than k_copy, you cannot afford to include this element, stop the inner loop.
Step 5: Update the Maximum Frequency
- After the inner loop finishes (either by exhausting k_copy or checking all previous elements), compare the number of matches you found with your current best answer.
- Update your answer if this frequency is higher.
Step 6: Final Return
- After checking all possible target elements from left to right, your answer variable will contain the maximum frequency that can be achieved.
- Return this as the result.
Frequency of the Most Frequent Element Example
Input: nums = [3, 2, 1, 4, 4, 7, 9], k = 5
Output: 4
Explanation: We can use indexes 0 and 1 and use 1 operation to make the index value at index 0 to 4 and use 2 operations to make values at index 1 to 4, this way we will have 4 occurrences of value 4.
Sort the Array
nums = [1, 2, 3, 4, 4, 7, 9]
Brute Force Dry Run
We will iterate from i = 1 to 6 and for each i, try to make previous elements equal to nums[i] using at most k = 5 operations.
i = 1 → nums[i] = 2
- cnt = 1, k_copy = 5
- j = 0 → nums[j] = 1 → diff = 1
→ k_copy = 4, cnt = 2
max freq so far = 2
i = 2 → nums[i] = 3
- cnt = 1, k_copy = 5
- j = 1 → nums[j] = 2 → diff = 1
→ k_copy = 4, cnt = 2 - j = 0 → nums[j] = 1 → diff = 2
→ k_copy = 2, cnt = 3
max freq so far = 3
i = 3 → nums[i] = 4
- cnt = 1, k_copy = 5
- j = 2 → nums[j] = 3 → diff = 1
→ k_copy = 4, cnt = 2 - j = 1 → nums[j] = 2 → diff = 2
→ k_copy = 2, cnt = 3 - j = 0 → nums[j] = 1 → diff = 3
→ k_copy = -1 (stop here)
max freq so far = 3
i = 4 → nums[i] = 4
- cnt = 1, k_copy = 5
- j = 3 → nums[j] = 4 → diff = 0
→ k_copy = 5, cnt = 2 - j = 2 → nums[j] = 3 → diff = 1
→ k_copy = 4, cnt = 3 - j = 1 → nums[j] = 2 → diff = 2
→ k_copy = 2, cnt = 4 - j = 0 → nums[j] = 1 → diff = 3
→ k_copy = -1
max freq so far = 4
i = 5 → nums[i] = 7
- cnt = 1, k_copy = 5
- j = 4 → nums[j] = 4 → diff = 3
→ k_copy = 2, cnt = 2 - j = 3 → nums[j] = 4 → diff = 3
→ k_copy = -1
max freq so far = 4
i = 6 → nums[i] = 9
- cnt = 1, k_copy = 5
- j = 5 → nums[j] = 7 → diff = 2
→ k_copy = 3, cnt = 2 - j = 4 → nums[j] = 4 → diff = 5
→ k_copy = -2
max freq so far = 4
Final Answer
The maximum frequency of any element after using at most 5 operations is: 4
This happens when elements 2, 3 are all made equal to 4.
Frequency of the Most Frequent Element Solution
Frequency of the Most Frequent Element Solution in C++
class Solution {
public:
int maxFrequency(vector<int>& nums, int k) {
// Get the size of the input array
int n = nums.size();
// Sort the array to align elements for minimal cost increments
sort(nums.begin(), nums.end());
// Variable to store the maximum frequency achievable
int ans = 1;
// Try each index as the target value to equalize all previous numbers to
for (int i = 1; i < n; ++i) {
// Start with a count of 1 for the current element itself
int cnt = 1;
// Copy of 'k' for this iteration, representing allowed total increments
int k_copy = k;
// Traverse backwards from index (i - 1) to 0
for (int j = i - 1; j >= 0; --j) {
// Calculate the cost to increment nums[j] up to nums[i]
int diff = nums[i] - nums[j];
// If the cost is within available increments
if (diff <= k_copy) {
// Deduct cost and include this element in count
k_copy -= diff;
cnt++;
}
// Stop if not enough k left to perform the operation
else {
break;
}
}
// Update the maximum frequency found so far
ans = max(ans, cnt);
}
// Return the final result
return ans;
}
};Frequency of the Most Frequent Element Solution in Java
class Solution {
// Function to calculate the maximum frequency of an element after at most k increments
public static int maxFrequency(int[] nums, int k) {
// Sort the array to align all elements for minimal increment cost
Arrays.sort(nums);
// Get the size of the array
int n = nums.length;
// Variable to store the result (maximum frequency)
int ans = 1;
// Try making each nums[i] the target value
for (int i = 1; i < n; i++) {
// Start with 1 (the target element itself)
int cnt = 1;
// Create a copy of k to track available increments for this i
int k_copy = k;
// Traverse all previous elements from (i - 1) to 0
for (int j = i - 1; j >= 0; j--) {
// Calculate the cost to increase nums[j] to nums[i]
int diff = nums[i] - nums[j];
// If we have enough increments to perform the operation
if (diff <= k_copy) {
k_copy -= diff;
cnt++;
}
// If not enough increments, break early
else {
break;
}
}
// Update the maximum frequency found so far
ans = Math.max(ans, cnt);
}
// Return the final answer
return ans;
}
}Frequency of the Most Frequent Element Solution in Python
class Solution:
def maxFrequency(self, nums: List[int], k: int) -> int:
# Sort the array to align all elements for minimal increment cost
nums.sort()
# Get the size of the array
n = len(nums)
# Initialize the maximum frequency result
ans = 1
# Try each index as the target value to match all previous elements
for i in range(1, n):
# Start count with the current element itself
cnt = 1
# Copy of k to track available increments for this attempt
k_copy = k
# Traverse previous elements from (i - 1) down to 0
for j in range(i - 1, -1, -1):
# Calculate the cost to make nums[j] equal to nums[i]
diff = nums[i] - nums[j]
# If enough operations left, include this element
if diff <= k_copy:
k_copy -= diff
cnt += 1
# If not enough operations, stop this loop
else:
break
# Update the result with the maximum frequency found so far
ans = max(ans, cnt)
# Return the final answer
return ans
Frequency of the Most Frequent Element Solution in Javascript
/**
* Function to find the maximum frequency of any element
* after performing at most k increments to increase other elements
* @param {number[]} nums - The input array
* @param {number} k - Maximum number of allowed increment operations
* @return {number}
*/
function maxFrequency(nums, k) {
// Sort the array to minimize cost of converting lower values to higher ones
nums.sort((a, b) => a - b);
// Get the number of elements
const n = nums.length;
// Store the result: maximum frequency found
let ans = 1;
// Try each element as the target value
for (let i = 1; i < n; i++) {
// Start with the current element
let cnt = 1;
// Copy of k to use during this loop
let k_copy = k;
// Traverse backward to convert earlier elements
for (let j = i - 1; j >= 0; j--) {
// Difference to bring nums[j] up to nums[i]
const diff = nums[i] - nums[j];
// If we have enough operations, convert and count
if (diff <= k_copy) {
k_copy -= diff;
cnt++;
} else {
// Not enough operations to include more
break;
}
}
// Update max frequency if current is better
ans = Math.max(ans, cnt);
}
// Return the final answer
return ans;
}Frequency of the Most Frequent Element Complexity Analysis
Time Complexity: O(n2)
Sorting the Array
The algorithm begins by sorting the array of size n. Sorting an array takes O(n log n) time, which is efficient and standard for most sorting algorithms like quicksort or mergesort.
Frequency Calculation (Brute Force)
After sorting, the algorithm examines each element in the array and tries to see how many previous elements can be increased (using the allowed k operations) to make them equal to the current element.
For each element:
- It looks at all the elements before it.
- For each of those elements, it calculates how much it would cost to increase it to match the current value.
- It keeps doing this until the total cost exceeds k.
In the worst case, for each element, it may need to examine all previous elements. That means:
- The first element does nothing.
- The second element checks 1 previous element.
- The third checks 2.
- ...
- The last element (at index n-1) may check up to n-1 elements.
This results in a sum of the first n integers, which grows quadratically. Mathematically, this sum is:
1 + 2 + 3 + ⋯ + (n−1) = n * (n−1) / 2
This is O(n²) time.
Total Time Complexity
So, the algorithm has:
- O(n log n) for sorting.
- O(n²) for the nested loop to calculate frequency by brute force.
Since O(n²) dominates O(n log n) for large n.
The total time complexity is: O(n2)
Space Complexity: O(1)
Auxiliary Space Complexity
This refers to any extra space used by the algorithm excluding the input and output.
- The algorithm uses a few integer variables:
n, ans, cnt, k_copy, i, j, etc.
→ All are simple scalar variables and require O(1) space. - No additional data structures (arrays, maps, etc.) are used.
→ So, auxiliary space is constant.
Auxiliary space = O(1)
Total Space Complexity
Input Space :
- The input is a vector nums of size n.
- It is passed by reference, but internally it is sorted in-place.
- So, no additional copy is made, and no extra space is used for storing input.
→ Input space = O(n) (but not counted in auxiliary).
Output Space :
- The output is a single integer value representing the max frequency.
- So, output space is O(1).
Overall Space Complexity = Input + Output + Auxiliary
Overall Space Complexity = O(n) + O(1) + O(1) = O(n)
Is the brute force approach efficient?
The brute-force solution has a time complexity of O(n²). This is because for each element in the array, we may look back at all previous elements to check how many can be incremented to match the current one using at most k operations.
Since n can be as large as 10⁵, the worst-case number of operations is approximately 10⁵ × 10⁵ = 10¹⁰.
This is far beyond the acceptable limit for most problems, where we are typically expected to stay within 10⁷ to 10⁸ operations. Therefore, the brute-force approach is not efficient for large inputs and will result in a Time Limit Exceeded (TLE).
An optimised approach is necessary to handle the upper limits of the input size.
Optimal Approach
In the brute-force solution, for every index i, we tried to look back at previous elements starting from i - 1 down to 0. For each element, we calculated how many operations it would take to increment it and make it equal to nums[i], continuing this process until we ran out of the allowed number of operations (k).
This second loop, running from j = i - 1 to 0, is what causes the overall time complexity to grow to O(n²).
Intuition Behind Optimisation
Now, to optimise this process, consider the case where the array nums is sorted in non-decreasing order. This is a powerful observation, because once sorted, we know that:
- Every element before nums[i] is either less than or equal to nums[i].
- That means we can only consider converting elements from the left side of i (i.e., elements smaller than nums[i]) to match nums[i], which is exactly what we want to do.
Now, imagine that in the brute-force loop, the pointer j stops at some value i - x, meaning we can use k or fewer operations to convert all the elements from index j to i into the same value as nums[i].
This gives us a window of length (i - j + 1) where all values can be made equal to nums[i].
In other words, we are aiming to convert each element in the subarray from nums[j] to nums[i] to the same value: nums[i].
What is the formula to calculate how many operations are needed to convert each element in the subarray from nums[j] to nums[i] to the same value: nums[i]?
To make all elements from nums[j] to nums[i] equal to nums[i], we need to bring each of the smaller elements up to nums[i]. The total number of operations required is the difference between the ideal total sum of this subarray (if all were nums[i]) and the actual sum of the elements in this subarray.
Mathematically:
Required operations = nums[i] × (i - j + 1) - sum of elements from j to i inclusive
nums[i] × (i - j + 1) represents the total sum if all elements were already equal to nums[i].
If this result is less than or equal to k, it means we have enough operations to convert that subarray to all nums[i].
We now have a powerful tool to compute how many operations are needed to make all elements in a subarray (from index j to i) equal to nums[i]. This means we no longer need to traverse from i-1 down to 0 for every nums[i] as in the brute-force approach.
Instead, we can optimise it by maintaining a left pointer j, which marks the leftmost index such that the number of operations needed to convert all elements from nums[j] to nums[i] is less than or equal to k.
How to make this work?
To make this work efficiently:
- We keep a running total of all elements inside the current window [j, i] using a variable called total.
- Every time we move the right pointer i forward (expanding the window), we add nums[i] to the total.
- At each step, we compute the number of operations
Required operations = nums[i] × window size - total
= nums[i] × (i - j + 1) - total - If the required operations exceed k, we shrink the window from the left by subtracting nums[j] from total and moving j one step to the right.
This way, we ensure that our window always contains a valid subarray where the elements can be made equal to nums[i] using at most k operations.
Maximising the Frequency
At each step, the size of the window (i - j + 1) represents the maximum frequency we can achieve for nums[i]. So we simply keep track of the maximum window size encountered during the process and return it as the final answer.
This approach avoids nested loops and leverages sorting, prefix sums, and the two-pointer sliding window technique, making it both elegant and efficient.
Frequency of the Most Frequent Element Algorithm
Step 1: Initialisation
- Get the size of the input array.
- Sort the array in non-decreasing order.
- Initialise two pointers:
- i → right end of the current window.
- j → left end of the window.
- Initialise a variable to keep track of the running total of the elements in the current window.
- Prepare to store or calculate the maximum frequency, which will be the size of the valid window.
Step 2: Expand the Window with Pointer i
- Start a loop that moves pointer i from left to right across the array.
- For every new i, add nums[i] to the running total.
- This means the window currently includes elements from index j to i.
Step 3: Compute the Cost to Make All Elements Equal
- The goal is to make all elements in the current window equal to nums[i] (the largest element in the window).
- Compute the ideal total sum if all elements in the window were equal to nums[i].
- Multiply nums[i] by the window size (i - j + 1).
- Calculate the number of increments needed as:
- ideal total minus the current total sum.
- If this difference is less than or equal to k, the window is valid.
Step 4: Shrink the Window When Needed
- If the required number of increments exceeds k, the window is invalid.
- To fix it, shrink the window by moving pointer j one step to the right.
- Also, subtract nums[j] from the running total.
- Only shrink once per i, even if the condition is still invalid.
Step 5: Track the Maximum Frequency
- After validating or shrinking the window, compute the current window size as (i - j + 1).
- Keep track of the maximum value of this size encountered so far.
Step 6: Return the Result
- After the loop finishes, return the largest valid window size, which represents the maximum frequency achievable with at most k operations.
Let us understand this with a video,
Animation of Frequency of the Most Frequent Element - Optimal Approach
Frequency of the Most Frequent Element Example
Input: nums = [3, 2, 1, 4, 4, 7, 9], k = 5
Output: 4
Explanation: We can use indexes 0 and 1 and use 1 operation to make the index value at index 0 to 4 and use 2 operations to make values at index 1 to 4, this way we will have 4 occurrences of value 4.
After Sorting
nums = [1, 2, 3, 4, 4, 7, 9]
Initial State
- i = 0, j = 0, tot = 0
- max_freq = i - j = 0
Iteration by Iteration
▶ i = 0
- tot += 1 → tot = 1
- new_tot = 1 * (0 - 0 + 1) = 1
- new_tot - tot = 0 ≤ 5 → valid
- No shrinking
- i - j = 0 → max_freq = 1
▶ i = 1
- tot += 2 → tot = 3
- new_tot = 2 * (1 - 0 + 1) = 4
- 4 - 3 = 1 ≤ 5 → valid
- i - j = 1 → max_freq = 2
▶ i = 2
- tot += 3 → tot = 6
- new_tot = 3 * 3 = 9
- 9 - 6 = 3 ≤ 5 → valid
- i - j = 2 → max_freq = 3
▶ i = 3
- tot += 4 → tot = 10
- new_tot = 4 * 4 = 16
- 16 - 10 = 6 > 5 → invalid
- Shrink once: tot -= nums[j] = 1 → tot = 9, j = 1
- Move to next i
- i - j = 3 - 1 = 2 → max_freq remains 3
▶ i = 4
- tot += 4 → tot = 13
- new_tot = 4 * 4 = 16
- 16 - 13 = 3 ≤ 5 → valid
- i - j = 4 - 1 = 3 → max_freq = 4
▶ i = 5
- tot += 7 → tot = 20
- new_tot = 7 * 5 = 35
- 35 - 20 = 15 > 5 → invalid
- Shrink once: tot -= nums[j] = 2 → tot = 18, j = 2
- Move to next i
- i - j = 5 - 2 = 3 → max_freq remains 4
▶ i = 6
- tot += 9 → tot = 27
- new_tot = 9 * 5 = 45
- 45 - 27 = 18 > 5 → invalid
- Shrink once: tot -= nums[j] = 3 → tot = 24, j = 3
- Move to next i
- i - j = 6 - 3 = 3 → max_freq remains 4
Final Result
The maximum frequency is: 4
→ Achieved when window = [2, 3, 4, 4], made equal to 4 using 3 operations.
Frequency of the Most Frequent Element leetcode Solution
Frequency of the Most Frequent Element leetcode Solution in C++
class Solution {
public:
int maxFrequency(vector<int>& nums, int k) {
// Sort the array to help build frequency from left to right
sort(nums.begin(), nums.end());
int n = nums.size();
long total = 0;
int j = 0, ans = 0;
// Use sliding window from j to i
for (int i = 0; i < n; ++i) {
total += nums[i]; // Add current number to total
// If the cost to make all elements in window equal to nums[i] exceeds k
while ((long)nums[i] * (i - j + 1) - total > k) {
total -= nums[j]; // Shrink window from left
j++;
}
// Update the result
ans = max(ans, i - j + 1);
}
return ans;
}
};Frequency of the Most Frequent Element leetcode Solution in Java
class Solution {
public static int maxFrequency(int[] nums, int k) {
Arrays.sort(nums); // Sort for consistent window behavior
int n = nums.length;
long total = 0;
int j = 0, ans = 0;
for (int i = 0; i < n; i++) {
total += nums[i]; // Add current number to running total
// Check if the cost exceeds k
while ((long)nums[i] * (i - j + 1) - total > k) {
total -= nums[j];
j++; // Shrink window from the left
}
ans = Math.max(ans, i - j + 1); // Update max frequency
}
return ans;
}
}Frequency of the Most Frequent Element leetcode Solution in Python
class Solution:
def maxFrequency(self, nums: list[int], k: int) -> int:
# Sort the array to allow making smaller elements equal to larger ones
nums.sort()
# Initialize the total sum of current window
total = 0
# Left pointer of the sliding window
j = 0
# Result to track the maximum frequency
ans = 0
# Traverse each element as the right end of the window
for i in range(len(nums)):
# Add current element to total sum
total += nums[i]
# Shrink the window if cost exceeds k
while nums[i] * (i - j + 1) - total > k:
total -= nums[j]
j += 1
# Update the maximum frequency found so far
ans = max(ans, i - j + 1)
# Return the result
return ansFrequency of the Most Frequent Element leetcode Solution in Javascript
/**
* @param {number[]} nums
* @param {number} k
* @return {number}
*/
var maxFrequency = function(nums, k) {
// Sort the array so that we can increment smaller numbers to match larger ones
nums.sort((a, b) => a - b);
let total = 0; // Sum of elements in the current window
let j = 0; // Left pointer of the sliding window
let ans = 0; // To store the maximum frequency
// Traverse each element as right end of the window
for (let i = 0; i < nums.length; i++) {
total += nums[i]; // Add current number to total sum
// Shrink the window from left if cost to equalize exceeds k
while (nums[i] * (i - j + 1) - total > k) {
total -= nums[j];
j++;
}
// Update the maximum frequency
ans = Math.max(ans, i - j + 1);
}
return ans;
};Frequency of the Most Frequent Element Complexity Analysis
Time Complexity: O(n logn)
High-Level Idea of the Code
This solution uses a sliding window approach:
- It maintains a window [j, i] where it tries to make all elements equal to nums[i] by increasing elements within the window using at most k operations.
- It keeps expanding the window (i++) and only shrinks it (j++) when the total required operations exceed k.
Time Complexity Breakdown :-
- Sorting the Array
- The array nums of size n is sorted first.
- Sorting takes O(n log n) time.
- Sliding Window Loop
- Pointers i and j are used to form a window.
- i moves from 0 to n-1.
- j also moves forward, but never more than n times.
Both i and j only move forward, and each moves at most n times.
So, the while loop runs in O(n) time overall.
Final Time Complexity
- Sorting: O(n log n)
- Sliding window traversal: O(n)
Overall Time Complexity : O(n logn)
Space Complexity: O(1)
Auxiliary Space Complexity:-
This includes any additional memory used by the algorithm, excluding input and output.
- The algorithm uses a few scalar variables:
i, j, tot, new_tot, n are all single integers or longs.
→ These take O(1) space. - No extra data structures (arrays, maps, etc.) are created.
→ Memory usage stays constant regardless of input size.
Auxiliary space = O(1)
Total Space Complexity:-
This includes any total memory used by the algorithm, including input and output space.
Input Space
- The input is a vector nums of size n.
- It is modified in-place (sorted), so no extra copy is made.
→ Input space = O(n) (not part of auxiliary space).
Output Space
- The output is a single integer (the maximum frequency).
→ Output space = O(1)
Overall Space Complexity = Input + Output + Auxiliary
Overall Space Complexity = O(n)+O(1)+O(1)=O(n)
Similar Problems
Now we have successfully tackled this problem, let's try these similar problems:-
You are given an integer array nums. A number x is lonely when it appears only once, and no adjacent numbers (i.e. x + 1 and x - 1) appear in the array.
Return all lonely numbers in nums. You may return the answer in any order.
You are given an array nums consisting of positive integers.
We call a subarray of nums nice if the bitwise AND of every pair of elements that are in different positions in the subarray is equal to 0.
Return the length of the longest nice subarray.
A subarray is a contiguous part of an array.
Note that subarrays of length 1 are always considered nice.
You are given a 0-indexed integer array nums and an integer k.
You can perform the following operation on the array at most k times:
- Choose any index i from the array and increase or decrease nums[i] by 1.
The score of the final array is the frequency of the most frequent element in the array.
Return the maximum score you can achieve.
The frequency of an element is the number of occurences of that element in the array.
You are given an integer array nums and two integers k and numOperations.
You must perform an operation numOperations times on nums, where in each operation you:
- Select an index i that was not selected in any previous operations.
- Add an integer in the range [-k, k] to nums[i].
Return the maximum possible frequency of any element in nums after performing the operations.
You are given a string s and an integer k. Your task is to find the maximum difference between the frequency of two characters, freq[a] - freq[b], in a substring subs of s, such that:
- subs has a size of at least k.
- Character a has an odd frequency in subs.
- Character b has a non-zero even frequency in subs.
Return the maximum difference.
Note that subs can contain more than 2 distinct characters.
You are given an integer array nums and two integers k and numOperations.
You must perform an operation numOperations times on nums, where in each operation you:
- Select an index i that was not selected in any previous operations.
- Add an integer in the range [-k, k] to nums[i].
Return the maximum possible frequency of any element in nums after performing the operations.