Skip to main content

Binary Search

Find the Smallest Divisor Given a Threshold Solution In C++/Java/Python/JS

Problem Description:

Given an array of integers nums and an integer threshold, we will choose a positive integer divisor, divide all the array by it, and sum the division's result. Find the smallest divisor such that the result mentioned above is less than or equal to threshold.
Each result of the division is rounded to the nearest integer greater than or equal to that element. (For example: 7/3 = 3 and 10/2 = 5).
The test cases are generated so that there will be an answer.
find-the-smallest-divisor-given-a-threshold-problem description

Examples:

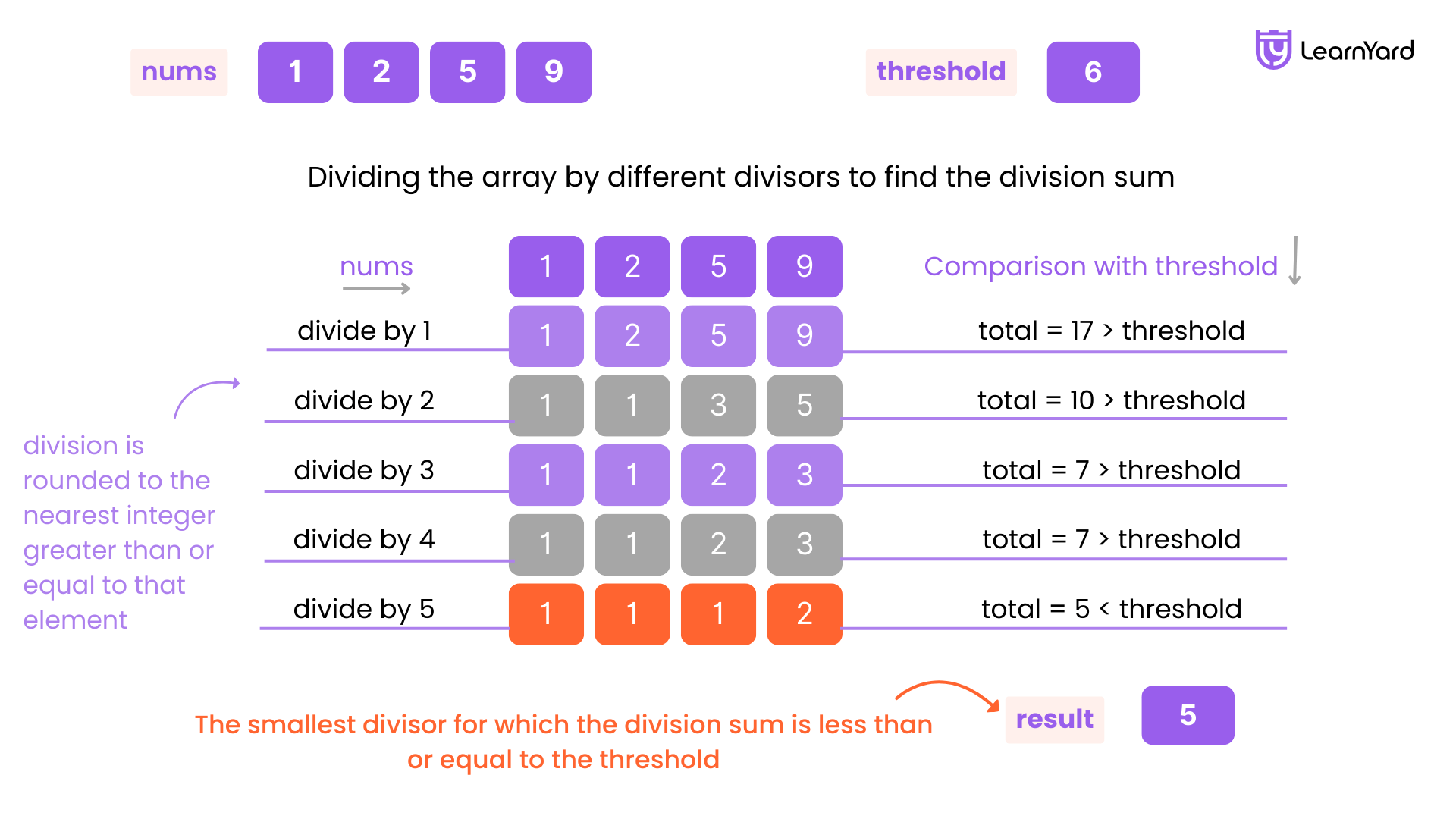
Input: nums = [1,2,5,9], threshold = 6
Output: 5
Explanation: We can get a sum to 17 (1+2+5+9) if the divisor is 1.
If the divisor is 4, we can get a sum of 7 (1+1+2+3) and if the divisor is 5, the sum will be 5 (1+1+1+2).

Input: nums = [44,22,33,11,1], threshold = 5
Output: 44
Explanation: If the divisor is 33, the sum will be 2 + 1 + 1 + 1 + 1 = 6.
If the divisor is 44, the sum will be 1 + 1 + 1 + 1 + 1 = 5, which is ≤ threshold (5). Thus, the smallest divisor that makes the sum ≤ 5 is 44.

Constraints:

1 <= nums.length <= 5 * 10⁴
1 <= nums[i] <= 10⁶
nums.length <= threshold <= 10⁶

Brute Force Approach

We are given an array nums where nums[i] represents an integer, and an integer threshold.

We need to find the smallest positive integer divisor such that when we divide each element in nums by this divisor and sum up the results (each rounded up to the nearest integer), the total sum is less than or equal to threshold.

Let's make some observations:

  1. What is the minimum divisor we can choose?
    The smallest divisor we can use is 1. Why? Because if we use 0, division is undefined, and using a smaller divisor would only increase the sum, making it harder to meet the threshold. The absolute minimum divisor is 1.
  2. What is the maximum divisor we can choose?
    The largest divisor we might need is the maximum element in nums. If we divide each number by itself, the result for each number will be 1, leading to the smallest possible sum (which is just the size of nums). Choosing a divisor greater than the maximum number is unnecessary, as it would yield the same result as using the maximum number itself.

Now that we know the minimum divisor (1) and the maximum divisor (max(nums)), we need to find the smallest divisor that results in a sum less than or equal to threshold.

It’s clear that the divisor must lie between these two limits:

  • If the divisor is smaller than 1, division is not possible.
  • If the divisor is larger than max(nums), it’s unnecessary because every number would be reduced to 1, giving the smallest possible sum.

Now we can start testing the divisor from the smallest possible value (1) up to the largest possible value (max(nums)), checking if the sum remains ≤ threshold.

For each value of d (divisor), we check if the sum of ceil(nums[i] / d) is within the threshold. If we find that it satisfies the condition for a certain d, we simply return that value of d as the answer.

Why?
Because it will be the smallest divisor that allows us to achieve a sum ≤ threshold. Any smaller divisor would result in a larger sum that exceeds the threshold.

Let's walk through the process step by step with the example nums = [1,2,5,9] and threshold = 6.

We need to find the smallest divisor that, when applied to all the numbers in nums, results in a sum of the divisions that is less than or equal to the threshold.

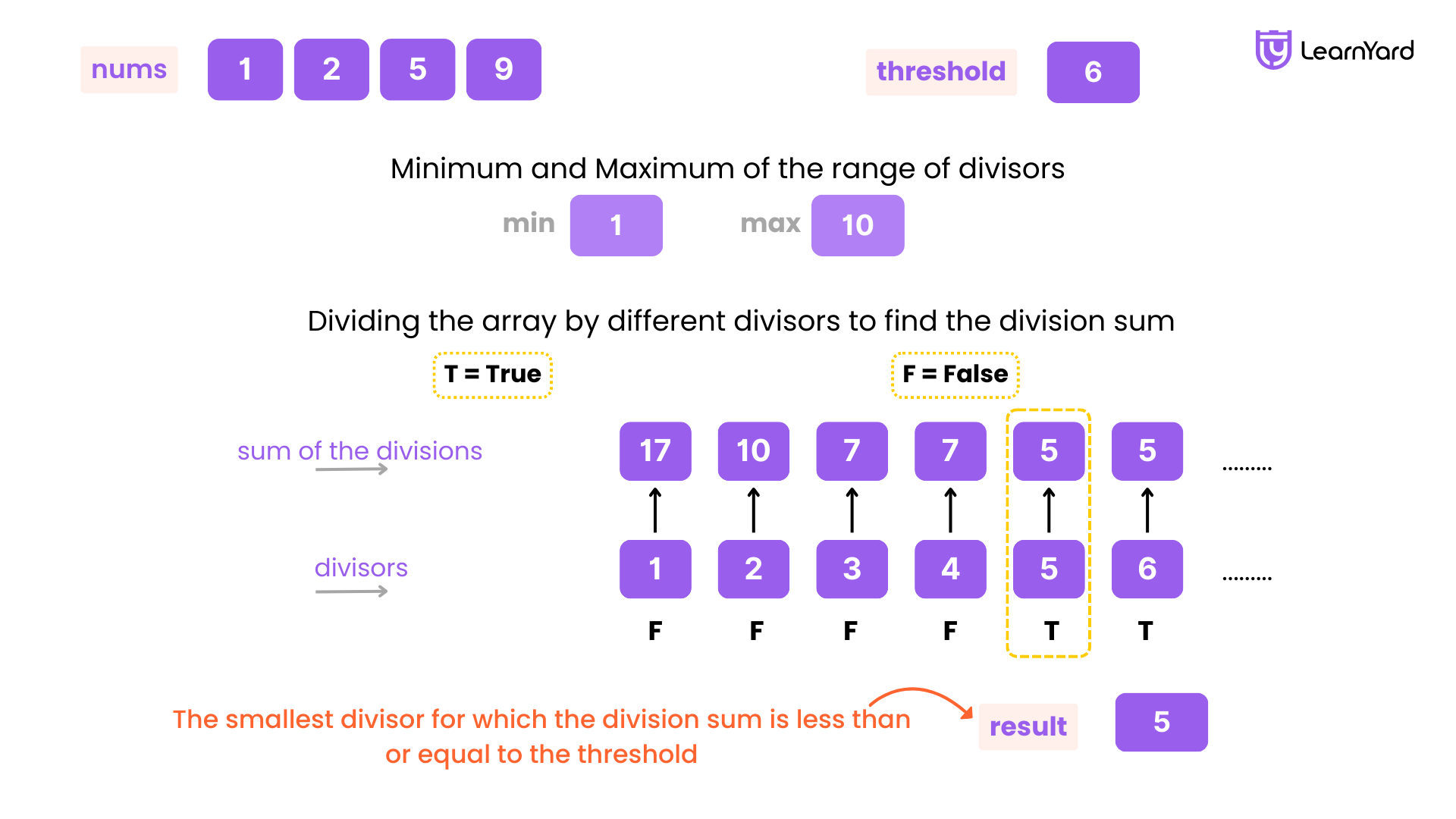
Range of Possible Divisors: The divisors we need to check range from 1 to max(nums), which is 9 in this case. So, we’ll check divisors from 1 to 9.

Checking Divisors:

    • Divisor 1: The sum of the divisions is 1 + 2 + 5 + 9 = 17, which is greater than the threshold (17 > 6). So, 1 doesn’t work.
    • Divisor 2: The sum of the divisions is 1 + 1 + 3 + 5 = 10, which is greater than the threshold (10 > 6). So, 2 doesn’t work.
    • Divisor 3: The sum of the divisions is 1 + 1 + 2 + 3 = 7, which is greater than the threshold (7 > 6). So, 3 doesn’t work.
    • Divisor 4: The sum of the divisions is 1 + 1 + 2 + 3 = 7, which is greater than the threshold (7 > 6). So, 4 doesn’t work.
    • Divisor 5: The sum of the divisions is 1 + 1 + 1 + 2 = 5, which is less than the threshold (5 < 6). So, 5 works!
    • Divisor 6: The sum of the divisions is 1 + 1 + 1 + 2 = 5, which is less than the threshold (5 < 6). So, 6 works!

After checking 5, we notice that any divisor greater than 5 (up to the maximum number in nums, which is 9) will also work. This is because the sum of the divisions will only continue to decrease as the divisor increases. Therefore, all divisors from 5 to 9 will satisfy the condition.

Since we are looking for the smallest divisor that works, 5 is the answer. Any divisor from 1 to 4 will always give a sum greater than the threshold, and any divisor from 5 to 9 will give a sum that is less than or equal to the threshold. Therefore, 5 is the smallest divisor that satisfies the condition.

In simple terms, once we find a divisor that works (in this case, 5), we know that all larger divisors will work too, but we want the smallest one. Hence, 5 is the answer!

Suppose x is the smallest divisor that works. This means that for any divisor from 1 to x-1, the sum of the divisions will always be greater than the threshold and will never satisfy the condition. But from x onwards, every divisor will give a sum that’s less than or equal to the threshold and will satisfy the condition.

So, once we find x (the smallest divisor that works), we know that all larger divisors will also work because the sum will only get smaller as the divisor increases. Since we’re looking for the smallest divisor that satisfies the condition, x is the answer.

find-the-smallest-divisor-given-a-threshold-example

How do we check if a divisor d is valid?

We can follow these steps:

  1. Start with a counter and set it to 0. This counter will keep track of the total sum after division.
  2. For every number in nums:
    • Divide the number by d and round it up using ceil(num / d).
    • Add this value to the counter.
    • This ensures that we add the division results after dividing all elements of nums by the divisor d.
  3. After processing all elements, check the value of the counter:
    • If the counter is ≤ threshold, then the divisor d is valid.
    • If the counter is > threshold, then the divisor d is too small, and we need to try a larger divisor.

This way, we can determine if a specific divisor d allows us to stay within the threshold.

💡
Try it Yourself!

Let's understand with an example:

Let's dry run the approach for nums = [1,2,5,9] and threshold = 6, strictly following the discussed approach.

Step 1: Identify the Search Range

  • Minimum divisor = 1
  • Maximum divisor = max(nums) = 9
  • We start testing divisors from 1 to 9, checking if the sum of ceil(nums[i] / d) is ≤ threshold.

Step 2: Test Each Divisor

Divisor = 1

  • Sum = ceil(1/1) + ceil(2/1) + ceil(5/1) + ceil(9/1)
  • 1 + 2 + 5 + 9 = 17 (> 6) → Not valid

Divisor = 2

  • Sum = ceil(1/2) + ceil(2/2) + ceil(5/2) + ceil(9/2)
  • 1 + 1 + 3 + 5 = 10 (> 6) → Not valid

Divisor = 3

  • Sum = ceil(1/3) + ceil(2/3) + ceil(5/3) + ceil(9/3)
  • 1 + 1 + 2 + 3 = 7 (> 6) → Not valid

Divisor = 4

  • Sum = ceil(1/4) + ceil(2/4) + ceil(5/4) + ceil(9/4)
  • 1 + 1 + 2 + 3 = 7 (> 6) → Not valid

Divisor = 5

  • Sum = ceil(1/5) + ceil(2/5) + ceil(5/5) + ceil(9/5)
  • 1 + 1 + 1 + 2 = 5 (≤ 6) → Valid

Since 5 is the smallest valid divisor, the output is 5.

Steps to Implement the Solution:

Define a helper function that checks whether a given divisor satisfies the condition:

  • Iterate through the array.
  • Compute ceil(num / divisor) for each element.
  • Sum up the results and compare with the threshold.
  • Return true if the sum is ≤ threshold, else return false.

Initialize search range:

  • Set minimum divisor = 1.
  • Set maximum divisor = max(nums).

Iterate through all possible divisors (1 to max(nums)):

  • Check if the divisor satisfies the threshold condition using the helper function.
  • If yes, return that divisor as the answer.

Return the smallest valid divisor found during iteration.

Code Implementation
1. C++ Try on Compiler 
class Solution {

    // Helper function to check if the sum of the divisions with divisor 'mid' is within the threshold
    bool check(vector<int>& nums, int threshold, int mid)
    {
        int sum = 0;

        // Iterate over all elements in the array
        for(auto &num: nums)
        {
            // Add the ceiling of the division result to the sum
            sum += ceil((double)num / mid);
        }

        // Return true if the sum is less than or equal to the threshold
        return sum <= threshold;
    }

public:

    // Main function to find the smallest divisor
    int smallestDivisor(vector<int>& nums, int threshold) {
        int ans = 0;
        // Minimum possible divisor is 1

        int mini = 1;

        // Maximum possible divisor is the largest number in the array
        int maxi = *max_element(nums.begin(), nums.end());

        // Iterate through all possible divisors from mini to maxi
        for(int i=mini; i<=maxi; i++)
        {

            // Check if this divisor satisfies the threshold condition
            if(check(nums, threshold, i))
            {

                // Return the smallest divisor that satisfies the condition
                return i;
            }
        }

        // If no valid divisor is found, return the initial answer
        return ans;
    }
};

2. Java Try on Compiler 
class Solution {
    // Helper function to check if the sum of the divisions with divisor 'mid' is within the threshold
    public boolean check(int[] nums, int threshold, int mid) {

        int sum = 0;

        // Iterate over all elements in the array
        for (int num : nums) {

            // Add the ceiling of the division result to the sum
            sum += Math.ceil((double) num / mid);
        }

        // Return true if the sum is less than or equal to the threshold
        return sum <= threshold;
    }

    public int smallestDivisor(int[] nums, int threshold) {
        int ans = 0;

        // Minimum possible divisor is 1
        int mini = 1;

        // Maximum possible divisor is the largest number in the array
        int maxi = Arrays.stream(nums).max().getAsInt();

        // Iterate through all possible divisors from mini to maxi
        for (int i = mini; i <= maxi; i++) {

            // Check if this divisor satisfies the threshold condition
            if (check(nums, threshold, i)) {
                
                // Return the smallest divisor that satisfies the condition
                return i;
            }
        }

        // If no valid divisor is found, return the initial answer
        return ans;
    }
}

3. Python Try on Compiler 
class Solution:
    # Helper function to check if the sum of the divisions with divisor 'mid' is within the threshold
    def check(self, nums, threshold, mid):

        sum = 0

        # Iterate over all elements in the array
        for num in nums:

            # Add the ceiling of the division result to the sum
            # Equivalent to math.ceil(num / mid)
            sum += -(-num // mid)  
        
        # Return true if the sum is less than or equal to the threshold
        return sum <= threshold

    def smallestDivisor(self, nums, threshold):
        ans = 0

        # Minimum possible divisor is 1
        mini = 1

        # Maximum possible divisor is the largest number in the array
        maxi = max(nums)

        # Iterate through all possible divisors from mini to maxi
        for i in range(mini, maxi + 1):

            # Check if this divisor satisfies the threshold condition
            if self.check(nums, threshold, i):

                # Return the smallest divisor that satisfies the condition
                return i

        # If no valid divisor is found, return the initial answer
        return ans

4. Javascript Try on Compiler 
/**
 * @param {number[]} nums
 * @param {number} threshold
 * @return {number}
 */
var check = function(nums, threshold, mid) {
    let sum = 0;

    // Iterate over all elements in the array
    for (let num of nums) {

        // Add the ceiling of the division result to the sum
        sum += Math.ceil(num / mid);
    }

    // Return true if the sum is less than or equal to the threshold
    return sum <= threshold;
};

var smallestDivisor = function(nums, threshold) {

    let ans = 0;

    // Minimum possible divisor is 1
    let mini = 1;

    // Maximum possible divisor is the largest number in the array
    let maxi = Math.max(...nums);

    // Iterate through all possible divisors from mini to maxi
    for (let i = mini; i <= maxi; i++) {

        // Check if this divisor satisfies the threshold condition
        if (check(nums, threshold, i)) {

            // Return the smallest divisor that satisfies the condition
            return i;
        }
    }

    // If no valid divisor is found, return the initial answer
    return ans;
};

Time Complexity: O(max(nums))

Initialization of Variables:
We initialize mini = 1 and maxi = max(nums), which takes O(n) time because finding the maximum element in the array nums requires scanning through all n elements.

Main Loop (for divisor i):
The main loop iterates from mini (1) to maxi (the maximum value in nums).
The number of iterations is O(maxi), where maxi is the maximum element in nums. In the worst case, maxi is equal to the size of nums (i.e., maxi = max(nums)).

Checking Divisibility (within check function):
For each divisor i, we call the check function, which iterates over all n elements of nums to calculate the sum.
The complexity of the check function is O(n).

Total Time Complexity:
The outer loop runs O(maxi) times (where maxi is the maximum element in nums).
Each iteration of the loop calls the check function, which runs in O(n) time.Hence, the overall time complexity is: O(max(nums))

Where:

  • maxi is the maximum value in nums.
  • n is the number of elements in nums.

Space Complexity: O(n)

  1. Auxiliary Space Complexity: O(1)
    The only extra space used is for the variables sum (in the check function) and i (in the main loop).
  2. Total Space Complexity: O(n)
    The input array nums takes O(n) space, where n is the length of the array.
    Therefore, the total space complexity is O(n).

Will Brute Force Work Against the Given Constraints? 

For the current solution, the time complexity is O(n * max(nums)), where n is the number of elements in the nums array (with an upper limit of 5 * 10⁴), and max(nums) is the maximum value in the array, which can be as large as 10⁶ in the worst-case scenario. This means the solution can handle up to approximately O(5 * 10⁴ * 10⁶) or O(5 * 10¹⁰) operations in the worst case.

However, given the constraints, the solution is not efficient enough for many typical inputs. In competitive programming environments, problems generally allow up to 10⁶ operations per test case. While the time complexity may exceed this for the worst-case scenario, most inputs will likely stay within a manageable range and execute efficiently within the given time limits.

Therefore, the O(n * max(nums)) time complexity does not guarantee that the solution will work efficiently for all input sizes within the problem's constraints. While it may perform well for typical inputs, it is crucial to consider the worst-case inputs that could push the solution beyond the upper limit. With careful optimization, it could perform well in most practical cases.

How to optimize it?

In the previous approach, we examined all possible divisors from the smallest to the largest and checked every divisor within that range to find the smallest divisor such that the sum of the division results is less than or equal to the threshold. This resulted in a time complexity of O(n * max(nums)), which was too slow and caused a TLE (Time Limit Exceeded) error.

Now, let’s think about improving this.
The main issue was that we checked every divisor from minimum to maximum, which took a lot of time.

Can we make this part faster?

Yes! Here’s the hint:

We are searching for the smallest divisor such that the sum of the division results is less than or equal to the threshold, and we know that this divisor lies between the minimum divisor (1) and the maximum divisor (the largest value in nums).

Now that we know the two endpoints, the minimum divisor (1) and the maximum divisor (max(nums)), let's make a few observations:

  1. The search space is sorted: The range of divisors, from the minimum divisor (1) to the maximum divisor (max(nums)), is naturally sorted.
  2. The search space is monotonic: If a certain divisor allows the sum of division results to be within the threshold, then any larger divisor will also work.
    If a certain divisor doesn’t work, then any smaller divisor will also fail.
  3. The middle element helps minimize or maximize the search space: If we take the middle value of the current range and check if the sum of the division results is less than or equal to the threshold, we can narrow the search space:
    If it works, we move to the left half to find a smaller valid divisor.
    If it doesn’t work, we move to the right half to find a larger divisor that works.

If we plot a graph with the range of divisors (from 1 to max(nums)) on the x-axis and the sum of divisions we get with a given divisor k on the y-axis, we observe the following:

For a given divisor, the sum of divisions will either be less than or equal to the threshold or greater than the threshold.

  • Before reaching the smallest valid divisor (let's call this mindivisor), the sum of divisions exceeds the threshold. This means that for any divisor less than mindivisor, the condition is not met, and we cannot achieve a valid sum within the threshold.
  • Once we reach mindivisor, the condition is satisfied, meaning the sum of the divisions of the array by the divisor becomes less than or equal to the threshold. From this point onward, every divisor greater than or equal to mindivisor will also satisfy the condition because increasing the divisor only reduces the division results, keeping the sum within the threshold. This trend continues as we move towards the maximum possible divisor (max(nums)).

Thus, mindivisor represents the smallest divisor that allows the sum to be less than or equal to the threshold. Once we find this divisor, any larger divisor will also satisfy the condition, but since we are looking for the smallest valid divisor, mindivisor is our answer.

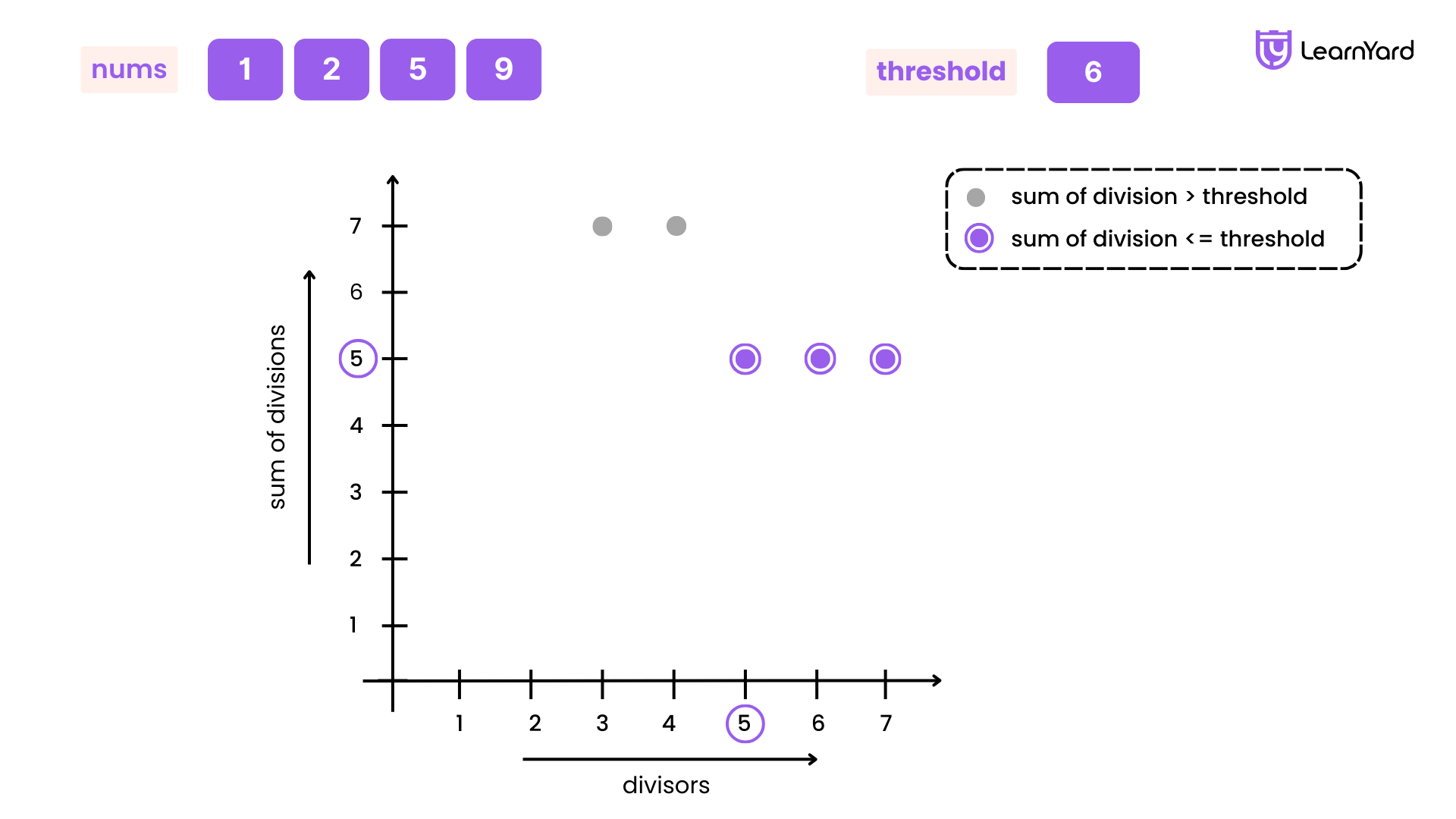
find-the-smallest-divisor-given-a-threshold-graph

With these points in mind, it's clear that instead of linearly checking all values from the minimum to the maximum divisor, we can take the middle value and continually reduce the search space.

Does this approach remind you of something you've seen before?

Yes, we are applying binary search here. By leveraging the sorted and monotonic properties of the divisor range, we efficiently narrow down the search space to find the minimum divisor that satisfies the condition of the problem, instead of checking each value linearly.

💡
How binary search works?

Binary search can help us quickly find the minimum divisor by narrowing down the range in each step

We can simply use binary search to determine the smallest divisor that results in a sum less than or equal to the threshold. Start by taking the middle value between the low (minimum divisor) and high (maximum divisor). If this mid-value satisfies the condition that the sum of division results is within the threshold, we store it as a potential answer and narrow the search space to the left half, looking for a smaller divisor. Otherwise, we move the search to the right half to find a larger valid divisor. We continue this process as long as low ≤ high.

Once the condition breaks, the stored answer is returned as the minimum divisor.

By using binary search, we can cut the search space in half at each step, which makes the solution much faster and avoids the TLE issue.

Let us understand this with a video,

0:00
/2:12

find-the-smallest-divisor-given-a-threshold-optimal approach animation explaination

💡
Try it Yourself!

Let's understand with an example:

Let’s dry run the binary search approach for the example nums = [1, 2, 5, 9] and threshold = 6.

Initial Setup:
low = 1 (minimum divisor)
high = 9 (maximum value in nums)

Step 1: Start the binary search
mid = (1 + 9) / 2 = 5

Step 2: Check if divisor 5 works

  • For divisor 5:
    • 1 / 5 = 1
    • 2 / 5 = 1
    • 5 / 5 = 1
    • 9 / 5 = 2
    • Sum = 1 + 1 + 1 + 2 = 5
  • Since 5 ≤ threshold, it works, so we update high = 4 (search in the left half).

Step 3: Recalculate mid for the new range

  • low = 1, high = 4
  • mid = (1 + 4) / 2 = 2

Step 4: Check if divisor 2 works

  • For divisor 2:
    • 1 / 2 = 1
    • 2 / 2 = 1
    • 5 / 2 = 3
    • 9 / 2 = 5
    • Sum = 1 + 1 + 3 + 5 = 10
  • Since 10 > threshold, it doesn't work. So, we update low = 3 (search in the right half).

Step 5: Recalculate mid for the new range

  • low = 3, high = 4
  • mid = (3 + 4) / 2 = 3

Step 6: Check if divisor 3 works

  • For divisor 3:
    • 1 / 3 = 1
    • 2 / 3 = 1
    • 5 / 3 = 2
    • 9 / 3 = 3
    • Sum = 1 + 1 + 2 + 3 = 7
  • Since 7 > threshold, it doesn't work. So, we update low = 4.

Step 7: Check divisor 4

  • low = 4, high = 4
  • mid = 4

For divisor 4:

  • 1 / 4 = 1
  • 2 / 4 = 1
  • 5 / 4 = 2
  • 9 / 4 = 3
  • Sum = 1 + 1 + 2 + 3 = 7
  • Since 7 > threshold, it doesn't work. So, low becomes 5.

Step 8: End condition

  • low = 5, high = 4, so the search stops, and the answer is 5.

Thus, the smallest divisor that allows the sum to be less than or equal to the threshold is 5.

How to code it up:

Define a helper function check:

  • This function takes the array nums, the threshold, and a divisor mid.
  • Loop through each element of nums, divide it by mid, round it up, and accumulate the sum.
  • Return true if the accumulated sum is less than or equal to the threshold; otherwise, return false.

Set up the binary search:

  • Initialize low to 1 and high to the maximum value in the array nums (i.e., max(nums)).

Binary search loop:

  • While low is less than or equal to high, calculate the middle value mid = (low + high) / 2.
  • Use the check function to determine if the current mid is a valid divisor:
    • If it works (i.e., check(nums, threshold, mid) returns true), update ans = mid and move the high pointer to mid - 1 to search for a smaller valid divisor.
    • If it doesn’t work, update low = mid + 1 to search for a larger valid divisor.

Return the answer:

  • Once the binary search completes, return the value of ans as the smallest divisor.
Code Implementation
1. C++ Try on Compiler 
class Solution {
    
    // Helper function to check if a divisor is valid
    bool check(vector<int>& nums, int threshold, int mid) {
        // Initialize sum to 0
        int sum = 0;

        // Loop through all the numbers in the array
        for (auto& num : nums) {
            // Add the ceil of the division of num by mid to sum
            sum += ceil((double)num / mid);
        }

        // Return true if the sum is within the threshold
        return sum <= threshold;
    }

public:
    // Main function to find the smallest divisor
    int smallestDivisor(vector<int>& nums, int threshold) {
        // Initialize the answer variable
        int ans = 0;

        // Set the low bound of the binary search
        int low = 1;

        // Set the high bound of the binary search to the max element of the
        // array
        int high = *max_element(nums.begin(), nums.end());

        // Perform binary search while the range is valid
        while (low <= high) {
            // Calculate the mid value of the range
            int mid = (low + high) / 2;

            // If mid is a valid divisor, update the answer and search the left
            // half
            if (check(nums, threshold, mid)) {
                ans = mid;
                high = mid - 1;
            }
            // If mid is not valid, search the right half
            else
                low = mid + 1;
        }

        // Return the answer
        return ans;
    }
};

2. Java Try on Compiler 
class Solution {
    // Helper function to check if a divisor is valid
    public boolean check(int[] nums, int threshold, int mid) {

        // Initialize sum to 0
        int sum = 0;

        // Loop through all the numbers in the array
        for (int num : nums) {
            // Add the ceil of the division of num by mid to sum
            sum += (int) Math.ceil((double) num / mid);
        }

        // Return true if the sum is within the threshold
        return sum <= threshold;
    }

    // Main function to find the smallest divisor
    public int smallestDivisor(int[] nums, int threshold) {

        // Initialize the answer variable
        int ans = 0;

        // Set the low bound of the binary search
        int low = 1;

        // Set the high bound of the binary search to the max element of the array
        int high = Arrays.stream(nums).max().getAsInt();

        // Perform binary search while the range is valid
        while (low <= high) {

            // Calculate the mid value of the range
            int mid = (low + high) / 2;

            // If mid is a valid divisor, update the answer and search the left half
            if (check(nums, threshold, mid)) {
                ans = mid;
                high = mid - 1;
            }
            
            // If mid is not valid, search the right half
            else {
                low = mid + 1;
            }
        }

        // Return the answer
        return ans;
    }

}

3. Python Try on Compiler 
class Solution(object):

    # Helper function to check if a divisor is valid
    def check(self, nums, threshold, mid):  

        # Initialize sum to 0
        total_sum = 0
        
        # Loop through all the numbers in the array
        for num in nums:

            # Add the ceil of the division of num by mid to sum
            # Equivalent to math.ceil(num / mid)
            total_sum += -(-num // mid)  
        
        # Return true if the sum is within the threshold
        return total_sum <= threshold

    # Main function to find the smallest divisor
    def smallestDivisor(self, nums, threshold):

        # Initialize the answer variable
        ans = 0
        
        # Set the low bound of the binary search
        low = 1
        
        # Set the high bound of the binary search to the max element of the array
        high = max(nums)

        # Perform binary search while the range is valid
        while low <= high:

            # Calculate the mid value of the range
            mid = (low + high) // 2
            
            # If mid is a valid divisor, update the answer and search the left half
            if self.check(nums, threshold, mid):  
                ans = mid
                high = mid - 1
                
            # If mid is not valid, search the right half
            else:
                low = mid + 1
        
        # Return the answer
        return ans

4. Javascript Try on Compiler 
/**
 * @param {number[]} nums
 * @param {number} threshold
 * @return {number}
 */

// Helper function to check if a divisor is valid
var check = function(nums, threshold, mid) {
    
    // Initialize sum to 0
    let sum = 0;

    // Loop through all the numbers in the array
    for (let num of nums) {
        // Add the ceil of the division of num by mid to sum
        sum += Math.ceil(num / mid);
    }

    // Return true if the sum is within the threshold
    return sum <= threshold;
}

var smallestDivisor = function(nums, threshold) {
    // Initialize the answer variable
    let ans = 0;

    // Set the low bound of the binary search
    let low = 1;

    // Set the high bound of the binary search to the max element of the array
    let high = Math.max(...nums);

    // Perform binary search while the range is valid
    while (low <= high) {

        // Calculate the mid value of the range
        let mid = Math.floor((low + high) / 2);

        // If mid is a valid divisor, update the answer and search the left half
        if (check(nums, threshold, mid)) {
            ans = mid;
            high = mid - 1;
        }

        // If mid is not valid, search the right half
        else {
            low = mid + 1;
        }
    }

    // Return the answer
    return ans;
};

Time Complexity: O(n * log(max(nums)))

Binary Search Complexity:
The search space for the divisor is between 1 and max(nums) (the largest element in the nums array). So, the range of possible divisors is [1, max(nums)].
Binary search operates by halving the search space with each iteration. Thus, the number of iterations is logarithmic with respect to the size of the range.
The number of binary search iterations is approximately O(log(max(nums))), where max(nums) is the largest element in the array.

Check Function Complexity:
In each binary search iteration, we call the check() function to verify if a particular divisor is valid.
The check() function loops through all the elements of the array nums and computes the sum of the divisions.
Since the array nums has n elements, the time complexity of the check() function is O(n).

Total Time Complexity:
In each binary search iteration, we perform a check() operation which takes O(n) time.
The number of binary search iterations is O(log(max(nums))).

Therefore, the total time complexity is: O(n * log(max(nums)))

Where:

  • n is the number of elements in nums.
  • max(nums) is the largest value in the nums array.

Space Complexity: O(n)

  1. Auxiliary Space Complexity: O(1)
    The space complexity is O(1) because we only use a constant amount of extra space (apart from the input data).
  2. Total Space Complexity: O(n)
    The input array nums takes O(n) space, where n is the size of nums.
    Therefore, the total space complexity is O(n).

Learning Tip

Now we have successfully tackled this problem, let's try these similar problems.

1. Capacity To Ship Packages Within D Days

A conveyor belt has packages that must be shipped from one port to another within D days.The ith package on the conveyor belt has a weight of weights[i]. Each day, we load the ship with packages on the conveyor belt (in the order given by weights). We may not load more weight than the maximum weight capacity of the ship.Return the least weight capacity of the ship that will result in all the packages on the conveyor belt being shipped within D days.

2. Sqrt(x)

Given a non-negative integer x, return the square root of x rounded down to the nearest integer. The returned integer should be non-negative as well.You must not use any built-in exponent function or operator.For example, do not use pow(x, 0.5) in C++ or x ** 0.5 in Python.

💡
Showcase your skills by joining LearnYard Technologies FZ-LLC as a Technical Content Writer. Apply now and inspire the next generation of learners—fill out the form: https://forms.gle/CGDsbGkcapSfvXKM8