Find the Duplicate Number Solution In C++/Java/Python/JS
Find the Duplicate Number Problem Description:
Given an array of integers nums containing n + 1 integers where each integer is in the range [1, n] inclusive.
There is only one repeated number in nums, return this repeated number.
You must solve the problem without modifying the array nums and using only constant extra space.
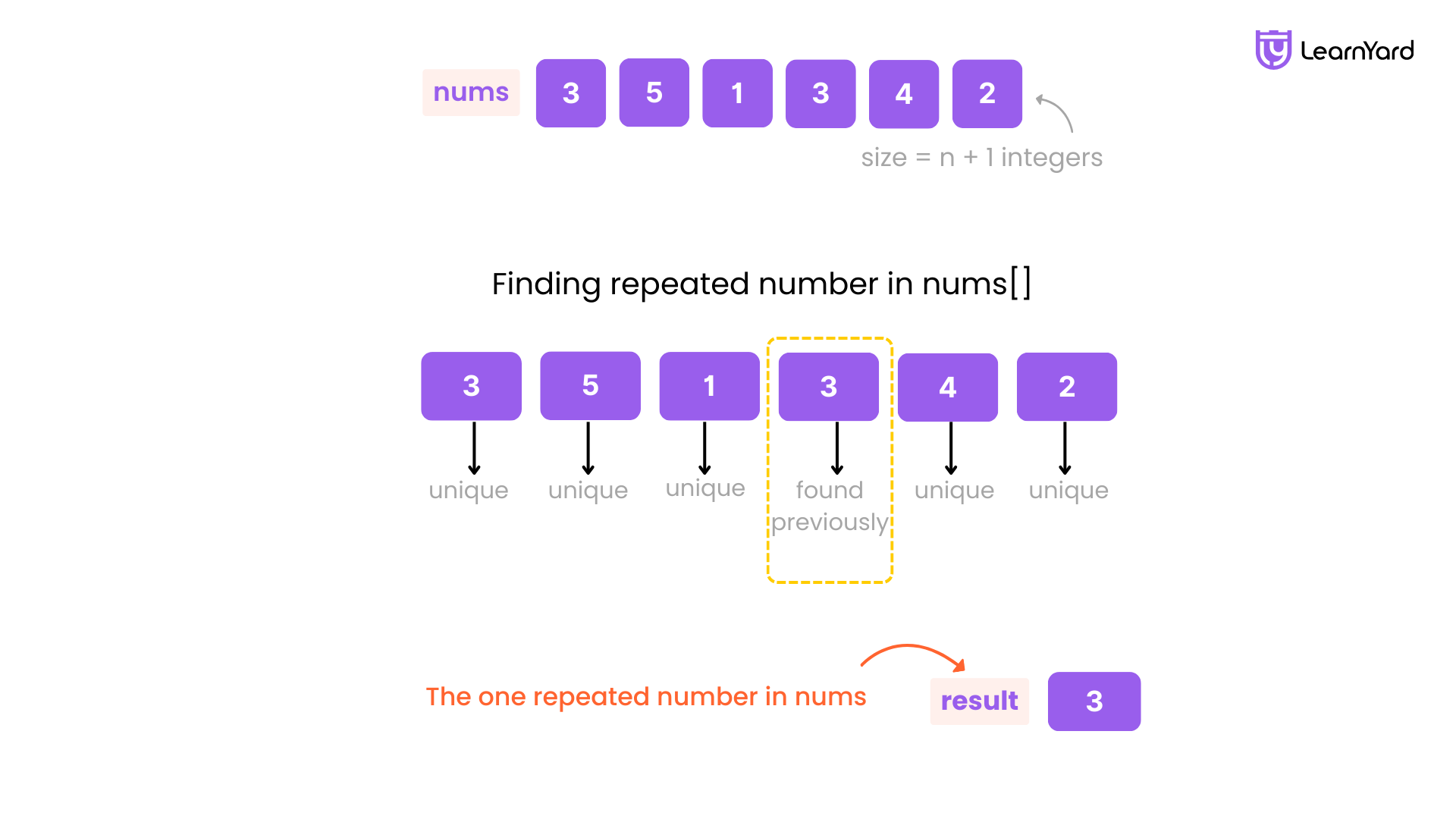
Examples:
Input: nums = [1,3,4,2,2]
Output: 2
Input: nums = [3,1,3,4,2]
Output: 3
Input: nums = [3,3,3,3,3]
Output: 3
Constraints:
1 <= n <= 10⁵
nums.length == n + 1
1 <= nums[i] <= n
All the integers in nums appear only once except for precisely one integer, which appears two or more times.
Brute Force Approach
Ok, let's understand the problem statement.
We need to find the repeated number in the given array nums. The array contains n + 1 integers, where each integer is in the range [1, n] inclusive.
Since there is only one repeated number, our task is to find and return it.
We can start iterating through nums, and for each element, we check whether it appears again later in the array. If we find a duplicate, we immediately return that number as the repeated element.
Function findDuplicate(nums):
For each num1 in nums:
For each num2 after num1 in nums:
If num1 == num2:
Return num1 (first duplicate found)
Return -1 (if no duplicate is found, though the problem guarantees one exists)For every element in nums, we are checking every element after it, leading to a time complexity of O(n²).
But wait! We can make a slight improvement, as we have a key observation:
- The search space is sorted
It's guaranteed that we have numbers in the range [1,n]. - The middle element helps minimize or maximize the search space
We have n + 1 numbers, but they are all in the range [1, n]. This means we are trying to fit n + 1 values into only n possible unique slots. Since there are more numbers than available unique values, at least one number must be repeated—this is what the Pigeonhole Principle tells us.
What is Pigeonhole Principle?
The Pigeonhole Principle is a simple but powerful concept in mathematics and logic. It states that:
"If you put more items into fewer containers than the number of items, at least one container must contain more than one item."
Imagine you have 6 pigeons but only 5 pigeonholes (small birdhouses). Since there are more pigeons than available spaces, at least one pigeonhole must contain more than one pigeon—there’s no way around it!
Now, let’s think about how we can use this idea to find the duplicate. Instead of directly looking at the array, we first guess a number that could be the duplicate. The way we guess is by picking a middle value mid from the range [1, n] (not from the array itself).
Once we have our guessed number mid, we count how many numbers in the array are less than or equal to mid. This count (cnt) tells us how many numbers fall in the range [1, mid].
- If cnt is greater than mid, this means that too many numbers are squeezed into the range [1, mid]. Normally, there should be at most mid numbers in this range, but we found more than that. This extra count suggests that a repeated number must be in this range.
- Otherwise, if cnt is less than or equal to mid, that means the repeated number must be in the higher range [mid + 1, n], because the lower half is behaving as expected.
By using this counting method, we can narrow down the possible location of the duplicate number step by step. Instead of checking every number pair, we use the number range itself to guide us toward the repeated value.
- The search space is monotonic
Once we know the answer is in one half, it would be found in that half because the search space is monotonic.
When we divide the range into two halves, we are essentially leveraging this structure to narrow down the potential location of the duplicate.
- If we find that there are too many numbers in the left half (count > mid), this tells us that the duplicate must be in this left part.
- On the other hand, if the count in the left half is within the expected range, then we can confidently say that the duplicate is in the right half.
This monotonic property (the idea that the numbers are ordered) helps us confidently eliminate one of the halves and continue searching only in the relevant half. By doing this iteratively, we reduce the possible search space, ensuring we can find the duplicate much faster.
With these conditions satisfied, we can confidently apply binary search here.
Instead of checking every element of nums and comparing it with every other element, we can efficiently apply binary search to narrow down the search space and find the duplicate more quickly.
Find the Duplicate Number Algorithm
Since the array contains n + 1 numbers but only n possible values (from 1 to n), at least one number must repeat. Here's why:
- There are more numbers in the array than the available number slots (values between 1 and n).
- The duplicate value must lie between 1 and n, as those are the only valid values for the elements in the array.
Thus, the idea is to search for the duplicate number within the range of 1 to n. The left boundary (left = 1) is the smallest value that could appear in the array, and the right boundary (right = n) is the largest possible value.
As long as left < right, we keep narrowing down our search space:
- Midpoint Calculation:
Calculate the midpoint of the current range by taking the average of left and right. This gives us a candidate number, mid.mid = (left + right) / 2 - Counting Numbers Less Than or Equal to Mid:
Count how many numbers in the array are less than or equal to mid. This tells us how many numbers fall in the range [1, mid]. - Why this helps?
- If the count of numbers less than or equal to mid is greater than mid, that means the number of values in [1, mid] is too large, implying that there must be a duplicate in this range. This is because, in a perfectly sorted array, there should be no more than mid numbers less than or equal to mid. The excess count indicates a duplicate within this range.
- If the count is less than or equal to mid, the duplicate must lie in the upper range, [mid + 1, n].
- Narrowing the Search Space
Based on the count comparison:If there are more numbers than expected in the [1, mid] range, update the search range to focus on the left half by setting right = mid.Otherwise, update the search range to the right half by setting left = mid + 1. - Repeat Until Convergence
This process is repeated, continually halving the search space based on the results of the counting step. - Find the Duplicate
Eventually, left == right, and at this point, the value at left (or right) is the duplicate number. This is because we've narrowed down the range to a single number where the duplicate must lie.
This improves the time complexity to O(n log n) instead of O(n²), making it much faster.
Find the Duplicate Number-BruteForce-Approach
Let's understand with an example:
Find the Duplicate Number Example:
Let's perform a concise dry run of the approach using the input nums = [3, 1, 3, 4, 2].
Step 1: Initialize Variables
- left = 1
- right = 4 (since n = 4, and the values in nums range from 1 to 4)
Step 2: Start the Binary Search LoopFirst Iteration
- mid = (left + right) / 2 = (1 + 4) / 2 = 2
- Count numbers in nums that are less than or equal to 2:
- nums = [3, 1, 3, 4, 2] → numbers ≤ 2 are [1, 2] → count = 2.
- Since count (2) is greater than mid (2), the duplicate must be in the left half of the range, i.e., in [1, 2].
- Update right = mid = 2.
Second Iteration
- mid = (left + right) / 2 = (1 + 2) / 2 = 1
- Count numbers in nums that are less than or equal to 1:
- nums = [3, 1, 3, 4, 2] → numbers ≤ 1 are [1] → count = 1.
- Since count (1) is not greater than mid (1), the duplicate must be in the right half of the range, i.e., in [2, 4].
- Update left = mid + 1 = 2.
Step 3: Exit Condition
- Now left = right = 2.
- Return left = 2, which is the duplicate number.
Final Output:
The duplicate number is 3.
Steps to Implement the Solution:
- Implement a Binary Search Function
- Initialize left = 0 and right = nums2.size() - 1.
- Use a while loop to search for the target in nums2.
- If nums2[mid] == target, return true.
- If nums2[mid] > target, search in the left half.
- Otherwise, search in the right half.
- If the element is not found, return false.
- Iterate Through nums1
- For each num in nums1, call binarySearch(nums2, num).
- If found, return num (smallest common element).
- Return -1 If No Common Element Exists
- If no match is found after checking all elements, return -1.
Find the Duplicate Number Leetcode Solution
Find the Duplicate Number Leetcode Solution / Code Implementation
1. Find the Duplicate Number solution in C++ Try on Compiler
class Solution {
public:
// Initialize the left and right boundaries of the search space
int findDuplicate(vector<int>& nums) {
// Initialize left and right boundaries
int left = 1, right = nums.size() - 1;
// Start binary search until left and right converge
while (left < right) {
// Calculate the mid point of the current range
int mid = left + (right - left) / 2; // Find the middle element
// Initialize the count of numbers <= mid
int count = 0;
// Count how many numbers are less than or equal to mid
for (int num : nums) {
if (num <= mid) {
// Increment count if num is less than or equal to mid
count++;
}
}
// If count is greater than mid, the duplicate must be in the left half
if (count > mid) {
// Narrow down the search space to the left half
right = mid;
} else {
// Otherwise, search in the right half
left = mid + 1;
}
}
// Return the found duplicate number
// When left == right, return the duplicate number
return left;
}
};
2. Find the Duplicate Number solution in Java Try on Compiler
class Solution {
// Function to find the duplicate number
public int findDuplicate(int[] nums) {
// Initialize left and right boundaries
int left = 1, right = nums.length - 1; // left is 1, right is n (nums.size() - 1)
// Perform binary search until left and right converge
while (left < right) {
// Calculate the middle element in the range
int mid = left + (right - left) / 2; // mid is the middle value
// Initialize count for numbers <= mid
int count = 0;
// Count how many numbers are less than or equal to mid
for (int num : nums) {
if (num <= mid) {
count++; // Increment count if num is less than or equal to mid
}
}
// If count is greater than mid, the duplicate must be in the left half
if (count > mid) {
right = mid; // Narrow down search space to the left half
} else {
left = mid + 1; // Otherwise, search in the right half
}
}
// Return the duplicate number found
return left; // When left == right, return the duplicate number
}
}
3. Find the Duplicate Number solution in Python Try on Compiler
class Solution:
# Function to find the duplicate number
def findDuplicate(self, nums):
# Initialize left and right boundaries
left, right = 1, len(nums) - 1 # left = 1, right = n
# Perform binary search until left and right converge
while left < right:
# Calculate the mid point of the current range
mid = left + (right - left) // 2 # mid is the middle value
# Initialize count of numbers <= mid
count = 0
# Count how many numbers are less than or equal to mid
for num in nums:
if num <= mid:
count += 1 # Increment count if num is less than or equal to mid
# If count is greater than mid, the duplicate must be in the left half
if count > mid:
right = mid # Narrow down the search space to the left half
else:
left = mid + 1 # Otherwise, search in the right half
# Return the found duplicate number
return left # When left == right, return the duplicate number
4. Find the Duplicate Number solution in Javascript Try on Compiler
var findDuplicate = function(nums) {
// Initialize left and right boundaries
let left = 1, right = nums.length - 1; // left = 1, right = n
// Perform binary search until left and right converge
while (left < right) {
// Calculate the middle element in the range
let mid = left + Math.floor((right - left) / 2); // mid is the middle value
// Initialize count for numbers <= mid
let count = 0;
// Count how many numbers are less than or equal to mid
for (let num of nums) {
if (num <= mid) {
count++; // Increment count if num is less than or equal to mid
}
}
// If count is greater than mid, the duplicate must be in the left half
if (count > mid) {
right = mid; // Narrow down the search space to the left half
} else {
left = mid + 1; // Otherwise, search in the right half
}
}
// Return the found duplicate number
return left; // When left == right, return the duplicate number
};
Find the Duplicate Number Complexity Analysis (Brute Force)
Time Complexity: O(n log m)
Let's analyze the time complexity of the algorithm.
- Binary Search Loop:The binary search loop runs while left < right, and each iteration reduces the search space by half.Therefore, the time complexity for the binary search loop is O(log n).
- The algorithm uses binary search to narrow down the range of possible duplicate numbers.
- In each iteration, we reduce the search space by half, because we adjust either the left or right boundary based on the count comparison.
In the worst case, the search space size reduces from n to 1 in log(n) iterations.
- Counting Numbers in the Array:
- In each iteration of the binary search, we count how many numbers in the array are less than or equal to mid.
- This requires iterating through all the n numbers in the array, which has a time complexity of O(n).
Combining the Two:
- The binary search loop runs O(log n) times, and in each iteration, we count the numbers in the array, which takes O(n) time.
Thus, the total time complexity is: O(n) × O(logn) = O(n logn)
Final Time Complexity: O(n log n)
Space Complexity: O(n)
- Auxiliary Space Complexity: O(1)
The algorithm only uses a few integer variables such as left, right, mid, and loop counters.
Therefore, the auxiliary space complexity is O(1). - Total Space Complexity: O(n)
The algorithm only uses the nums array provided as input, and no additional arrays or data structures are created. The algorithm operates in-place by modifying the left and right pointers to narrow down the search range.
Thus, the total space complexity is O(n). The only space used is for the input array nums, and no new arrays are allocated during the process.
Will Brute Force Work Against the Given Constraints?
For the current solution, the time complexity is O(n log n), where n is the number of elements in the nums array (1 ≤ n ≤ 10⁵) and nums.length == n + 1.
In the worst-case scenario, we iterate through all elements of nums (O(n)), and for each element, we perform a binary search to count the number of elements less than or equal to mid (O(log n)).
This results in a total time complexity of O(n log n). While n can be as large as 100,000, log n (which is approximately 17 for n = 100,000) ensures that the number of operations remains manageable, leading to around 1.7 × 10⁶ operations in the worst case.
This approach is much more efficient than a brute-force solution with a time complexity of O(n²), which would be infeasible for large inputs. The binary search significantly reduces the number of comparisons, making the solution efficient even for the largest inputs within the given constraints.
Given the constraints where 1 ≤ nums[i] ≤ n, and all integers in nums appear only once except for precisely one integer that appears twice or more, this solution ensures that we find the duplicate in an efficient manner.
While there may be more optimal approaches for some specific scenarios, this algorithm is well-suited for the problem's constraints and guarantees a balance between simplicity and performance.
Can we optimize it?
As we traverse nums, we are looking for the duplicate number. Given that nums contains n + 1 integers in the range [1, n], the Pigeonhole Principle guarantees that at least one number must appear twice, because there are more numbers than there are possible values in the range.
But how can we efficiently check for the duplicate in nums?
We can use a hashtable to quickly check if an element is present.
What is a hashtable?
A HashTable is a data structure used to store key-value pairs, where each key maps to a value. In this case, we can use the number in nums as the key and use an array as the table to store the count of how many times each number appears.
The idea is simple:
We can use a hash table (which can be efficiently represented by an array) to track the count of each number we encounter.
Since each number in the array lies within the range [1, n], we can use the value itself as an index in the array (acting like a hash table) and increment its count when we encounter that number.
Here's the simple approach:
- Create a count array: We initialize an array of size n+1 (as numbers range from 1 to n) to store the count of each number from nums.
- Traverse the array: For each number in nums, use the number as the index in the count array. If the count at that index is 1, we increment it. If it’s already 2 (indicating the number has appeared before), we return that number immediately as the duplicate.
Find the Duplicate Number-Optimal-Approach
Let's understand with an example:
Find the Duplicate Number Example:
Input: nums = [1, 3, 4, 2, 2]
Create a count array: count = [0, 0, 0, 0, 0].
Traverse through the array:
For 1: count[1] = 1.
For 3: count[3] = 1.
For 4: count[4] = 1.
For 2: count[2] = 1.
For 2: count[2] = 2 → Since it’s 2, return 2 as the duplicate.
Input: nums = [3, 1, 3, 4, 2]
Similarly, 3 will be found as the first repeated number.
Steps to Implement the Solution:
Step 1: Create an array count of size n+1 initialized to 0.
Step 2: Traverse through nums:
- For each element, use it as the index and check the count in the array.
- If the count is already 1, return that element immediately as the duplicate.
- Otherwise, increment the count for that index.
Find the Duplicate Number Leetcode Solution
Find the Duplicate Number Leetcode Solution / Code Implementation
1. Find the Duplicate Number solution in C++ Try on Compiler
class Solution {
public:
int findDuplicate(vector<int>& nums) {
// Get the size of the array
int n = nums.size();
// Create a count array to store the frequency of each number
vector<int> count(n+1, 0);
// Traverse through the array
for(auto num: nums) {
// If the count of the number is already 1, it means it's a duplicate
if(count[num] == 1)
return num;
// Increment the count for the current number
count[num]++;
}
// Return -1 if no duplicate is found (shouldn't happen as per problem constraints)
return -1;
}
};2. Find the Duplicate Number solution in Java Try on Compiler
class Solution {
// Function to find the duplicate number
public int findDuplicate(int[] nums) {
// Get the size of the array
int n = nums.length;
// Create a count array to store the frequency of each number
int[] count = new int[n + 1];
// Traverse through the array
for (int num : nums) {
// If the count of the number is already 1, it means it's a duplicate
if (count[num] == 1) {
return num;
}
// Increment the count for the current number
count[num]++;
}
// Return -1 if no duplicate is found (shouldn't happen as per problem constraints)
return -1;
}
}
3. Find the Duplicate Number solution in Python Try on Compiler
class Solution(object):
def findDuplicate(self, nums):
# Get the size of the array
n = len(nums)
# Create a count array to store the frequency of each number
count = [0] * (n + 1)
# Traverse through the array
for num in nums:
# If the count of the number is already 1, it means it's a duplicate
if count[num] == 1:
return num
# Increment the count for the current number
count[num] += 1
# Return -1 if no duplicate is found (shouldn't happen as per problem constraints)
return -1
4. Find the Duplicate Number solution in Javascript Try on Compiler
/**
* @param {number[]} nums
* @return {number}
*/
var findDuplicate = function (nums) {
// Get the size of the array
const n = nums.length;
// Create a count array to store the frequency of each number
const count = new Array(n + 1).fill(0);
// Traverse through the array
for (let num of nums) {
// If the count of the number is already 1, it means it's a duplicate
if (count[num] === 1) {
return num;
}
// Increment the count for the current number
count[num]++;
}
// Return -1 if no duplicate is found (shouldn't happen as per problem constraints)
return -1;
};Find the Duplicate Number Complexity Analysis (Hashtable)
Time Complexity: O(n)
Let's break down the approach step-by-step to analyze the time complexity:
- Initializing the Count Array:
- We initialize the count array of size n+1 (where n is the number of elements in nums).
- This takes O(n) time because we create an array of size n+1 and initialize each element to 0.
- Traversing Through the nums Array:
- We then iterate through the nums array to count the occurrences of each number.
- The length of nums is n+1, so iterating through this array takes O(n) time.
- Updating the Count Array:
- For each element in nums, we perform a constant time operation: checking the count and updating the count array.
- Therefore, the count update for each element is O(1).
- Returning the Result:
- As soon as we find the duplicate (the count of an element becomes 2), we return it immediately. This is also O(1).
Overall Time Complexity:
- The overall time complexity is the sum of the time complexities of the steps:
- O(n) for initializing the count array
- O(n) for iterating through the nums array and checking the counts.
Thus, the total time complexity is O(n).
Space Complexity: O(n)
- Auxiliary Space Complexity: O(n)
The algorithm only uses a count array of size n+1 (where n is the number of elements in the nums array). The array stores integer values, so it only requires O(n) space.
Therefore, the auxiliary space complexity is O(n). - Total Space Complexity: O(n)
The algorithm uses an additional count array of size n+1, which takes up O(n) space.
Therefore, the total space complexity is O(n).
Can there be a more optimized approach?
Alright! Let’s break this down step by step in a super simple way. Imagine you have a list of numbers, and you know that one number appears twice. Your job is to find that number without changing the list and without using extra space.
At first, this might seem tricky because usually, to find a duplicate, we’d use a hash table (extra memory) or sort the array (which modifies it). But here, we’re going to use a completely different and clever approach.
Think of an array like this:
nums = [3, 1, 3, 4, 2]
Each number in the array tells us where to jump next.
For example:
- Index 0 → 3 (Go to index 3)
- Index 1 → 1 (Go to index 1)
- Index 2 → 3 (Go to index 3)
- Index 3 → 4 (Go to index 4)
- Index 4 → 2 (Go to index 2)
Instead of thinking of this as an array, let's visualize it as a directed graph (or a linked list-like structure):
- Start at index 0 → the value is 3, so we jump to index 3.
- At index 3, the value is 4, so we jump to index 4.
- At index 4, the value is 2, so we jump to index 2.
- At index 2, the value is 3, so we jump back to index 3 → We have a loop!
This forms a sort of "loop" or cycle because one number (the duplicate) causes us to revisit an index more than once.
Notice that when we arrive at index 3, we follow the chain of jumps and eventually end up back at index 3.
This is because index 2 is pointing to index 3, and index 3 is already in our path.
The array has n+1 numbers but only n unique values.
- The numbers in the array range from 1 to n (i.e., 1 ≤ nums[i] ≤ n).
- This means that at least one number must be repeated because we have n+1 slots but only n possible distinct values.
- Since every number acts as a "pointer," at least one pointer must point to an already visited index, forming a cycle.
This cycle tells us that there’s a duplicate number, and the duplicate number is the entrance to the cycle.
Since the array behaves like a linked list with a cycle, we can use Floyd’s Cycle Detection Algorithm (Tortoise and Hare method) to efficiently find the entrance of the cycle.
- The slow pointer moves one step at a time.
- The fast pointer moves two steps at a time.
- Since there is a cycle, the fast pointer will eventually catch up to the slow pointer inside the loop.
- Then, resetting one pointer to the beginning and moving both one step at a time will lead both to the duplicate number—which is the entrance of the cycle.
Find the Duplicate Number-Optimized-Approach
Floyd’s Cycle Detection Algorithm (Tortoise and Hare Algorithm)
Floyd’s Cycle Detection Algorithm is a clever technique used to detect cycles in a sequence of numbers where each element acts as a pointer to the next. It is commonly applied in linked lists, but in our case, we use it on an array where each number represents a jump to an index. The idea is to use two pointers—a slow pointer (tortoise) that moves one step at a time and a fast pointer (hare) that moves two steps at a time. If there is a cycle (which must exist due to the constraints of the problem), the fast pointer will eventually catch up to the slow pointer inside the cycle.
Once they meet, we reset one pointer to the start of the array while keeping the other at the meeting point. Now, both move one step at a time. The place where they meet again is the entrance of the cycle—which corresponds to the duplicate number. This happens because the distance from the start to the cycle entrance is the same as the distance from the meeting point to the entrance when moving at the same speed.
This algorithm is efficient because it runs in O(n) time and uses O(1) extra space, making it an optimal solution for detecting duplicate numbers in this problem without modifying the array.
Think of it like a maze:
- Each number tells you which door to go through.
- Eventually, because one room (number) appears more than once, you will re-enter a room you’ve already been in—forming a loop.
- The first room you re-enter is the duplicate number.
That’s how this method finds the duplicate efficiently!
Find the Duplicate Number Algorithm
- Understanding the Cycle Concept:
- Each number in the array represents an index to jump to.
- Since there are n + 1 numbers in the range [1, n], at least one number must repeat, forming a cycle.
- Detecting the Cycle:
- Use two pointers:
- Slow pointer (tortoise): Moves one step at a time.
- Fast pointer (hare): Moves two steps at a time.
- If there’s a duplicate, the fast pointer will eventually catch up to the slow pointer inside the cycle.
- Use two pointers:
- Finding the Duplicate Number:
- Reset one pointer to the start of the array.
- Move both pointers one step at a time until they meet again.
- The meeting point is the duplicate number.
Let's understand with an example:
Find the Duplicate Number Example:
Step 1: Detect Cycle (Find Meeting Point)
- Initialization:
- Slow = nums[0] → nums[3] → 4
- Fast = nums[nums[0]] → nums[nums[3]] → nums[4] → 2
- Iteration 1:
- Slow moves to nums[4] → 2
- Fast moves to nums[nums[2]] → nums[3] → 4
- Iteration 2:
- Slow moves to nums[2] → 3
- Fast moves to nums[nums[4]] → nums[2] → 3
- Both pointers meet at 3, confirming a cycle.
Step 2: Find Duplicate
- Reset Slow to nums[0] → 3
- Move both pointers one step at a time
- Slow = nums[3] → 4
- Fast = nums[3] → 4
- Slow = nums[4] → 2
- Fast = nums[4] → 2
- Slow = nums[2] → 3
- Fast = nums[2] → 3
- Pointers meet at 3, which is the duplicate.
- Return 3.
How to code it up:
- Initialize two pointers:
- slow and fast, both starting at nums[0].
- Find the cycle:
- Move slow one step at a time: slow = nums[slow].
- Move fast two steps at a time: fast = nums[nums[fast]].
- Keep moving until slow == fast (cycle detected).
- Find the duplicate number:
- Reset slow to nums[0].
- Move both slow and fast one step at a time until they meet again.
- Return the meeting point (which is the duplicate number).
Find the Duplicate Number Leetcode Solution
Find the Duplicate Number Leetcode Solution / Code Implementation
1. Find the Duplicate Number solution in C++ Try on Compiler
class Solution {
public:
int findDuplicate(vector<int>& nums) {
// Step 1: Initialize two pointers, slow and fast
int slow = nums[0];
int fast = nums[0];
// Step 2: Move slow by one step and fast by two steps until they meet
do {
slow = nums[slow]; // Move slow by one step
fast = nums[nums[fast]]; // Move fast by two steps
} while (slow != fast); // Loop until both pointers meet (detect cycle)
// Step 3: Reset slow to the start of the array
slow = nums[0];
// Step 4: Move both slow and fast one step at a time to find duplicate
while (slow != fast) {
slow = nums[slow]; // Move slow by one step
fast = nums[fast]; // Move fast by one step
}
// Step 5: Return the duplicate number where both pointers meet
return slow;
}
};
2. Find the Duplicate Number solution in Java Try on Compiler
class Solution {
public int findDuplicate(int[] nums) {
// Step 1: Initialize two pointers, slow and fast
int slow = nums[0];
int fast = nums[0];
// Step 2: Move slow by one step and fast by two steps until they meet
do {
slow = nums[slow]; // Move slow by one step
fast = nums[nums[fast]]; // Move fast by two steps
} while (slow != fast); // Loop until both pointers meet (detect cycle)
// Step 3: Reset slow to the start of the array
slow = nums[0];
// Step 4: Move both slow and fast one step at a time to find duplicate
while (slow != fast) {
slow = nums[slow]; // Move slow by one step
fast = nums[fast]; // Move fast by one step
}
// Step 5: Return the duplicate number where both pointers meet
return slow;
}
}
3. Find the Duplicate Number solution in Python Try on Compiler
class Solution:
def findDuplicate(self, nums):
# Step 1: Initialize two pointers, slow and fast
slow = nums[0]
fast = nums[0]
# Step 2: Move slow by one step and fast by two steps until they meet
while True:
slow = nums[slow] # Move slow by one step
fast = nums[nums[fast]] # Move fast by two steps
if slow == fast: # Loop until both pointers meet (detect cycle)
break
# Step 3: Reset slow to the start of the array
slow = nums[0]
# Step 4: Move both slow and fast one step at a time to find duplicate
while slow != fast:
slow = nums[slow] # Move slow by one step
fast = nums[fast] # Move fast by one step
# Step 5: Return the duplicate number where both pointers meet
return slow
4. Find the Duplicate Number solution in Javascript Try on Compiler
var findDuplicate = function(nums) {
// Step 1: Initialize two pointers, slow and fast
let slow = nums[0];
let fast = nums[0];
// Step 2: Move slow by one step and fast by two steps until they meet
do {
slow = nums[slow]; // Move slow by one step
fast = nums[nums[fast]]; // Move fast by two steps
} while (slow !== fast); // Loop until both pointers meet (detect cycle)
// Step 3: Reset slow to the start of the array
slow = nums[0];
// Step 4: Move both slow and fast one step at a time to find duplicate
while (slow !== fast) {
slow = nums[slow]; // Move slow by one step
fast = nums[fast]; // Move fast by one step
}
// Step 5: Return the duplicate number where both pointers meet
return slow;
};
Find the Duplicate Number Complexity Analysis (Two Pointers)
Time Complexity: O(n)
Let's break down the time complexity of the Floyd's Tortoise and Hare (Cycle Detection) algorithm:
- Phase 1: Finding the intersection point (cycle detection)
- In the first phase, we move the slow pointer by one step at a time and the fast pointer by two steps at a time.
- This continues until the slow and fast pointers meet. In the worst case, the fast pointer will traverse through the entire array (i.e., O(n)), where n is the number of elements in the array.
- The time complexity for this phase is O(n).
- Phase 2: Finding the entrance to the cycle (duplicate number)
- After detecting the cycle (when the slow and fast pointers meet), we reset the slow pointer to the start of the array.
- Both pointers (slow and fast) now move one step at a time and continue until they meet again.
- This phase also involves O(n) steps in the worst case, as we are traversing the array linearly.
Overall Time Complexity:
Since both phases each involve a linear scan through the array, the total time complexity is:
O(n) + O(n) = O(n)
Thus, the time complexity of this algorithm is O(n), where n is the number of elements in the array.
Space Complexity: O(n)
- Auxiliary Space Complexity: O(1)
The algorithm only uses a few integer variables: slow, fast (pointers for traversal).
Therefore, the auxiliary space complexity is O(1). - Total Space Complexity: O(n + m)
Since we have an input array nums of size n.
Therefore, the total space complexity is O(n)
Bonus Approach!
Let’s explore one more bonus approach to solve this efficiently.
You have an array nums of size n + 1. The array contains integers between 1 and n (inclusive), and one integer is repeated. Your task is to find this repeated number.
The idea is to use the binary representation of numbers and analyze their individual bits. We will count the bits of each number and compare these counts to identify the repeated number.
Every integer can be expressed as a binary number, a sequence of 0s and 1s. For example:
1 in binary is 00000001
2 in binary is 00000010
3 in binary is 00000011
4 in binary is 00000100
Each digit in the binary representation is called a bit. In this example, there are 8 bits, but in most cases, numbers are represented in a fixed number of bits (like 32 bits or 64 bits depending on the system).
We are given an array of numbers in the range [1, n] where exactly one number is repeated. The core insight is that the repeated number will cause an imbalance in the bit counts at certain positions.
Let’s break this down:
- If we examine the first bit (bit 0) of all the numbers in the array, we would expect approximately half of them to be 0 and the other half to be 1, assuming no duplicate exists. This is because, in the binary representation of numbers from 1 to n, the first bit follows a balanced distribution—even numbers have 0, and odd numbers have 1—ensuring an almost equal split.
- But if one number appears twice, it will contribute an extra 1 in the bit position where it has a 1. This will cause the count of 1s in that position to exceed what is expected.
For example, let’s look at the following array:
nums = [3, 1, 3, 4, 2]
3 in binary is 00000011
1 in binary is 00000001
3 in binary is 00000011
4 in binary is 00000100
2 in binary is 00000010
If we examine the bits in positions from bit 0 to bit 7, we can observe that some positions will have more 1s than expected due to the repeated number.
Let’s focus on counting the 1s for each bit position across all numbers.
- For bit 0: The numbers 1 and 3 have a 1 in bit 0, so we count 2 ones in bit 0.
- For bit 1: The numbers 1, 3, and 2 have a 1 in bit 1, so we count 3 ones in bit 1.
Now, we also know that in the range [1, n] (which is [1, 4] in this case), we would expect each bit position to have about half the numbers with a 1 and the other half with a 0.
For bit 0, in the range [1, 4], we should expect:
1 → bit 0 is 1
2 → bit 0 is 0
3 → bit 0 is 1
4 → bit 0 is 0
So, we expect 2 ones in bit 0. But because of the repeated number (3), we get 3 ones, which is one more than expected.
The key observation is that the repeated number is the one that adds an extra 1 to the bit positions. So, if a bit position has more 1s than expected, that means the repeated number has a 1 in that bit position.
Bit 0 has 3 ones (1 more than expected) → the repeated number has a 1 in bit 0.
Bit 1 has 3 ones (1 more than expected) → the repeated number has a 1 in bit 1.
By collecting the bits where we see an imbalance, we can reconstruct the repeated number.
Once we know which bits have an imbalance, we can rebuild the repeated number by combining those bits. Each bit position contributes to forming the duplicate number, so we can use the bitwise OR operation to combine them and get the final result.
Conclusion:
The idea is to count the 1s in each bit position for all the numbers in the array and compare these counts to the expected counts from the range [1, n].
- Any bit position with more 1s than expected is due to the repeated number, and we can use that information to reconstruct the duplicate number.
- If one number is repeated in the array, it will cause an imbalance in the bit counts.
- For example, if the number 3 is repeated, it will increase the count of 1s in the bits where 3 has 1s in its binary form.
Find the Duplicate Number Algorithm
- We'll iterate through the bit positions from 0 to log(n) (since there are at most log(n) bits needed to represent numbers in the range [1, n]).
- For each bit position, we will count how many numbers in the array have a 1 at that position.
- We'll also count the number of 1s expected at each bit position from the range [1, n].
- We compare the bit counts for each bit position:
- If the count of 1s in a given bit position is more than expected (which is approximately half of the total numbers for that bit), we know that the duplicate number has a 1 in that bit position.
- Once we identify the bit positions that have an excess of 1s (due to the repeated number), we can reconstruct the duplicate number by combining these bits.
- We will use the bitwise OR operation to combine bits that are set (i.e., 1 in a specific position) to form the final duplicate number.
This approach works efficiently in O(n log n) time because for each bit (which can be up to log(n) bits in the worst case), we examine each number, and the space complexity is O(1) since we only need to store a few variables to count the bits.
Find the Duplicate Number-Bonus-Approach
Let's understand with an example:
Find the Duplicate Number Example:
Let's perform a concise dry run of the bit manipulation approach on the given input:
Input:
nums = [3,1,3,4,2]
Step 1: Determine Bit Positions
- The numbers range from 1 to 4, meaning we need log2(4) = 2 bits (bit 0 and bit 1).
- We count 1s in each bit position for both nums and [1, n].
Step 2: Count 1s in Each Bit Position
Bit 0 Counts
Binary Representation:
- 1 → 0001 (bit 0 = 1)
- 2 → 0010 (bit 0 = 0)
- 3 → 0011 (bit 0 = 1)
- 4 → 0100 (bit 0 = 0)
Expected count from [1, 4] = 2 ones
nums = [3,1,3,4,2]:
- 3 → 0011 (bit 0 = 1)
- 1 → 0001 (bit 0 = 1)
- 3 → 0011 (bit 0 = 1)
- 4 → 0100 (bit 0 = 0)
- 2 → 0010 (bit 0 = 0)
Actual count in nums = 3 ones (Extra 1 due to duplicate)
Bit 1 Counts
Binary Representation:
- 1 → 0001 (bit 1 = 0)
- 2 → 0010 (bit 1 = 1)
- 3 → 0011 (bit 1 = 1)
- 4 → 0100 (bit 1 = 0)
Expected count from [1, 4] = 2 ones
nums = [3,1,3,4,2]:
- 3 → 0011 (bit 1 = 1)
- 1 → 0001 (bit 1 = 0)
- 3 → 0011 (bit 1 = 1)
- 4 → 0100 (bit 1 = 0)
- 2 → 0010 (bit 1 = 1)
Actual count in nums = 3 ones (Extra 1 due to duplicate)
Step 3: Reconstruct the Duplicate Number
- Bit 0 has extra 1 → Duplicate has bit 0 set
- Bit 1 has extra 1 → Duplicate has bit 1 set
Reconstructing the number: (Bit 1 = 1, Bit 0 = 1) → 11 in binary → 3
Final Output:
Duplicate Number = 3
How to code it up:
- Initialize Required Variables
- n = nums.size() - 1 → Since the array has n+1 elements, the numbers are in range [1, n].
Loop Through Each Bit Position
- We iterate through each bit position from 0 to 31 (assuming 32-bit integers).
- At each bit position bit, we will count how many numbers have 1 in that bit.
Count the 1s in the Current Bit Position
- Count 1s in nums → Loop through the array and count how many numbers have a 1 at bit position bit.
- Count 1s in range [1, n] → Count how many numbers from 1 to n have a 1 at bit position bit.
Identify the Extra 1s Due to the Duplicate
- If the count of 1s in nums is greater than the expected count, this means the duplicate number has a 1 in this bit position.
- Use bitwise OR (|=) to set the bit in the duplicate variable.
Return the Duplicate Number
- After processing all bit positions, the duplicate variable will store the repeated number.
- Return duplicate as the final answer.
- duplicate = 0 → This variable will store the duplicate number.
Find the Duplicate Number Leetcode Solution
Find the Duplicate Number Leetcode Solution / Code Implementation
1. Find the Duplicate Number solution in C++ Try on Compiler
class Solution {
public:
int findDuplicate(vector<int>& nums) {
int n = nums.size() - 1; // Since there are n+1 elements, the range is [1, n]
int duplicate = 0;
// Iterate over each bit position from 0 to 31 (assuming we work with 32-bit integers)
for (int bit = 0; bit < 32; ++bit) {
int count = 0;
int expected_count = 0;
// Count how many numbers in the array have a 1 in the current bit position
for (int num : nums) {
if (num & (1 << bit)) {
count++;
}
}
// Count how many numbers from 1 to n have a 1 in the current bit position
for (int i = 1; i <= n; ++i) {
if (i & (1 << bit)) {
expected_count++;
}
}
// If count exceeds the expected count, the repeated number has a 1 in this bit position
if (count > expected_count) {
duplicate |= (1 << bit); // Set the corresponding bit in the duplicate number
}
}
return duplicate;
}
};
2. Find the Duplicate Number solution in Java Try on Compiler
class Solution {
public int findDuplicate(int[] nums) {
int n = nums.length - 1; // Since there are n+1 elements, the range is [1, n]
int duplicate = 0;
// Iterate over each bit position from 0 to 31 (for 32-bit integers)
for (int bit = 0; bit < 32; bit++) {
int count = 0;
int expectedCount = 0;
// Count how many numbers in the array have a 1 in the current bit position
for (int num : nums) {
if ((num & (1 << bit)) != 0) {
count++;
}
}
// Count how many numbers from 1 to n have a 1 in the current bit position
for (int i = 1; i <= n; i++) {
if ((i & (1 << bit)) != 0) {
expectedCount++;
}
}
// If count exceeds the expected count, the repeated number has a 1 in this bit position
if (count > expectedCount) {
duplicate |= (1 << bit); // Set the corresponding bit in the duplicate number
}
}
return duplicate;
}
}
3. Find the Duplicate Number solution in Python Try on Compiler
class Solution:
def findDuplicate(self, nums):
n = len(nums) - 1 # Since there are n+1 elements, the range is [1, n]
duplicate = 0
# Iterate over each bit position from 0 to 31 (for 32-bit integers)
for bit in range(32):
count = 0
expected_count = 0
# Count how many numbers in the array have a 1 in the current bit position
for num in nums:
if num & (1 << bit):
count += 1
# Count how many numbers from 1 to n have a 1 in the current bit position
for i in range(1, n + 1):
if i & (1 << bit):
expected_count += 1
# If count exceeds the expected count, the repeated number has a 1 in this bit position
if count > expected_count:
duplicate |= (1 << bit) # Set the corresponding bit in the duplicate number
return duplicate
4. Find the Duplicate Number solution in Javascript Try on Compiler
var findDuplicate = function(nums) {
let n = nums.length - 1; // Since there are n+1 elements, the range is [1, n]
let duplicate = 0;
// Iterate over each bit position from 0 to 31 (for 32-bit integers)
for (let bit = 0; bit < 32; bit++) {
let count = 0;
let expectedCount = 0;
// Count how many numbers in the array have a 1 in the current bit position
for (let num of nums) {
if (num & (1 << bit)) {
count++;
}
}
// Count how many numbers from 1 to n have a 1 in the current bit position
for (let i = 1; i <= n; i++) {
if (i & (1 << bit)) {
expectedCount++;
}
}
// If count exceeds the expected count, the repeated number has a 1 in this bit position
if (count > expectedCount) {
duplicate |= (1 << bit); // Set the corresponding bit in the duplicate number
}
}
return duplicate;
};
Find the Duplicate Number Complexity Analysis (Bit Manipulation)
Time Complexity: O(n)
The algorithm iterates over 32 bits (assuming a 32-bit integer) and, for each bit, it performs two loops:
- Counting bits in nums
- Counting bits in the range [1, n]
Breaking it down step-by-step:
- Outer loop: Runs for 32 iterations (since integers are at most 32-bit).
- Inner loops: Each inner loop runs through O(n) elements.
- Total operations per bit position: O(n) + O(n) = O(2n) = O(n).
- Total complexity: Since we iterate over 32 bits, the overall complexity is:
O(32 * n) = O(n)
(Since 32 is a constant, it simplifies to O(n).
Space Complexity: O(n)
- Auxiliary Space Complexity: O(1)
The algorithm only uses a few integer variables: duplicate, count, expected_count (for counting bits and storing the duplicate number).
Therefore, the auxiliary space complexity is O(1). - Total Space Complexity: O(n + m)
Since we have an input array nums of size n, the input itself takes O(n) space.
Therefore, the total space complexity is O(n)
Similar Problems
When working with an array, finding duplicate numbers efficiently is a common challenge. The Two Pointers technique can help in detecting cycles in problems like Find the Duplicate Number in an Array, similar to Floyd’s cycle detection algorithm. Binary Search can also be used to find the duplicate by narrowing down the search space based on element counts. Another powerful approach is Bit Manipulation, specifically using XOR, which helps in problems like Find the Duplicate Number Using XOR, leveraging the properties of XOR to identify repeated elements. In languages like Java, optimized solutions for Find the Duplicate Number in an Array Java often utilize these techniques for efficiency. Combining these methods allows for solving the problem with minimal space and time complexity.
Now that we have successfully tackled this problem, let's try similar problems.
Given an unsorted integer array nums. Return the smallest positive integer that is not present in nums.
You must implement an algorithm that runs in O(n) time and uses O(1) auxiliary space.
Given a non-empty array of integers nums, every element appears twice except for one. Find that single one.
You must implement a solution with a linear runtime complexity and use only constant extra space.
Given the head of a linked list, return the node where the cycle begins. If there is no cycle, return null.
There is a cycle in a linked list if there is some node in the list that can be reached again by continuously following the next pointer. Internally, pos is used to denote the index of the node that tail's next pointer is connected to (0-indexed). It is -1 if there is no cycle. Note that pos is not passed as a parameter.
Do not modify the linked list.
Given an array nums containing n distinct numbers in the range [0, n], return the only number in the range that is missing from the array.
5. Set Mismatch
You have a set of integers s, which originally contains all the numbers from 1 to n. Unfortunately, due to some error, one of the numbers in s got duplicated to another number in the set, which results in repetition of one number and loss of another number.
You are given an integer array nums representing the data status of this set after the error.
Find the number that occurs twice and the number that is missing and return them in the form of an array.