Find Minimum in Rotated Sorted Array II Solution In C++/Java/Python/JS
Problem Description:
Suppose an array of length n, sorted in ascending order, is rotated between 1 and n times. For example, the array nums = [0,1,4,4,5,6,7] might become:
- [4,5,6,7,0,1,4] if it was rotated 4 times.
- [0,1,4,4,5,6,7] if it was rotated 7 times.
Notice that rotating an array [a[0], a[1], a[2], ..., a[n-1]] 1 time results in the array [a[n-1], a[0], a[1], a[2], ..., a[n-2]].
Given the sorted rotated array nums that may contain duplicates, return the minimum element of this array.
You must decrease the overall operation steps as much as possible.
Examples:
Input: nums = [1,3,5]
Output: 1
Explanation: The minimum element in nums is 1.
Input: nums = [2,2,2,0,1]
Output: 0
Explanation: The minimum element in nums is 0.
Constraints:
- n == nums.length
- 1 <= n <= 5000
- -5000 <= nums[i] <= 5000
- nums is sorted and rotated between 1 and n times.
Given a sorted, rotated array, our task is to identify and return the minimum element.
For now, let's ignore the sorted and rotated array context and focus on the general problem of identifying the smallest element in any array. How would you approach this?
Brute Force Approach
Intuition:
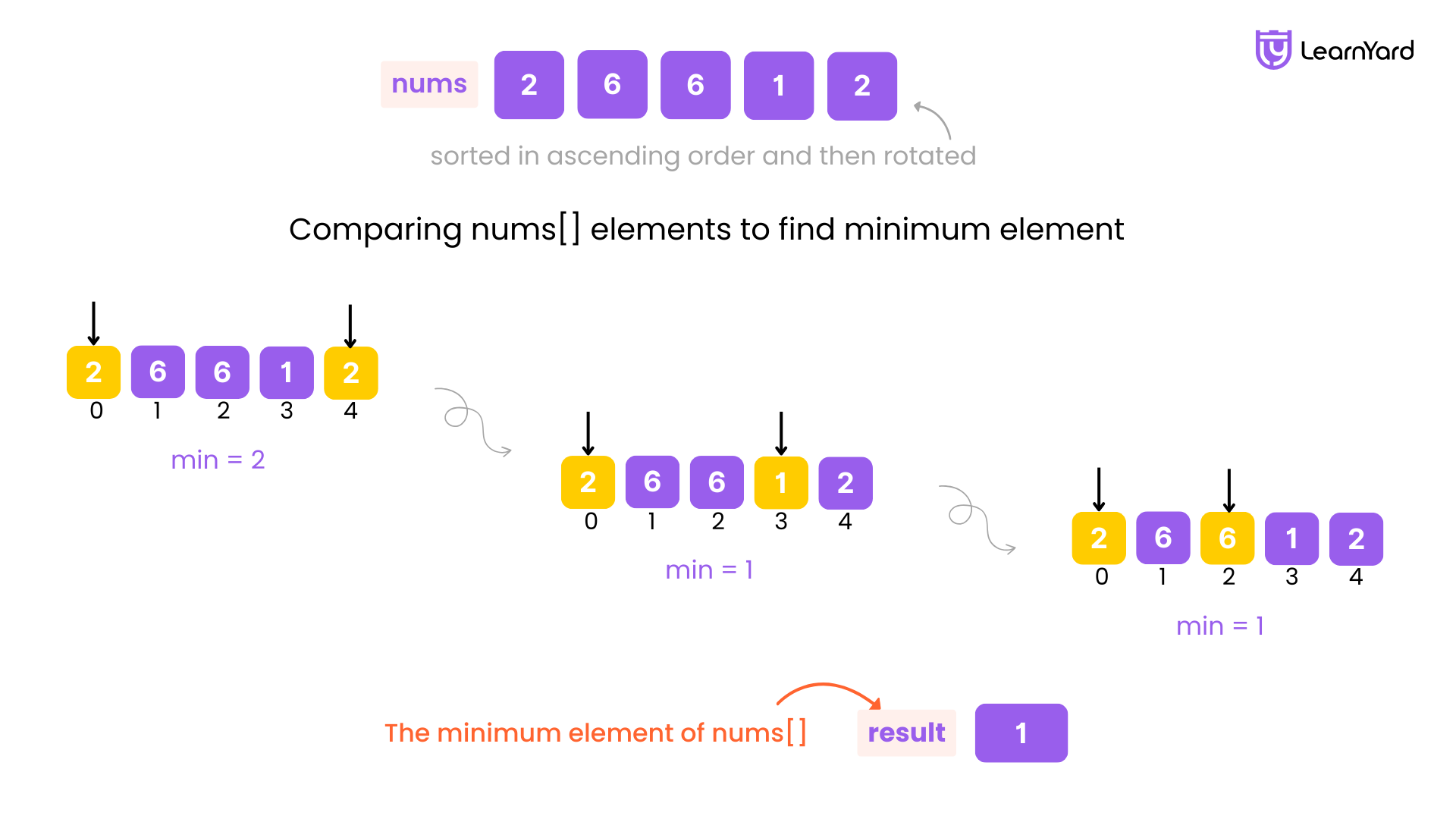
To address this problem, we can utilise a straightforward approach. The idea is to find and minimise the value throughout the entire array.
Imagine an answer variable that will store the minimum element we encounter as we iterate through the array. We'll initialize our answer with the value of the first element of the array since it's a good starting point.
Next, we start iterating through the array from the second element (i.e., index 1). For each element at index i, we compare it with the value stored in our variable (which holds the minimum value found up to the previous element, i.e., index i-1). If the current element (nums[i]) is smaller than the value in our variable, we update the variable with this new, smaller value.
We continue this comparison for each element in the array, updating the variable whenever we find a smaller value. By the time we finish iterating through the array, the variable will hold the smallest element in the entire array.
Finally, we return the value stored in this variable as the minimum element of the array.
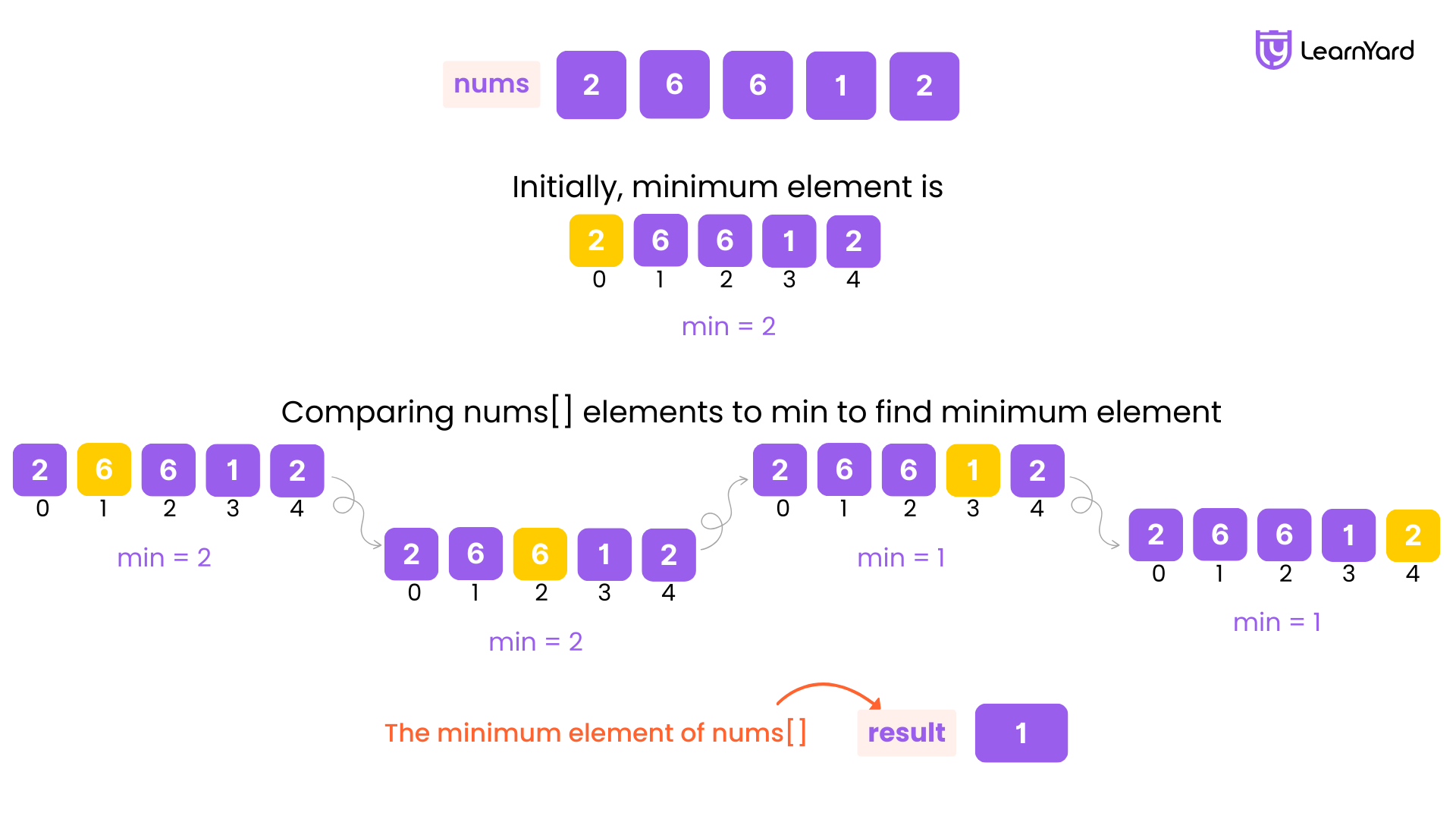
Find Minimum in Rotated Sorted Array II Example
Input: nums = [4, 9, 11, 2, 2, 4]
Output: 2
Explanation: The minimum element in nums is 2.
Initialization:
- The variable ans is initialized with the first element of the array.
Iteration:
- The size of the array n is 6.
- We start iterating from the second element (index 1):
- First iteration (i = 1)
- nums[1] = 9
- Compare 9 with ans (4): ans remains 4
- Second iteration (i = 2):
- nums[2] = 11
- Compare 11 with ans (4): ans remains 4
- Third iteration (i = 3):
- nums[3] = 2
- Compare 2 with ans (4): ans is updated to 2
- Fourth iteration (i = 4):
- nums[4] = 4
- Compare 2 with ans (2): ans remains 2
- Fifth iteration (i = 5):
- nums[5] = 4
- Compare 4 with ans (2): ans remains 2.
- After completing all iterations, the variable ans holds the minimum element of the array, which is 2.
- The function returns ans.
Find Minimum in Rotated Sorted Array II Algorithm
Step 1: Initialize the Minimum Variable:
- Start by initializing an ans variable to store the minimum element. Set it to the first element of the array.
Step 2: Iterate Through the Array:
- Use a loop to go through each element of the array starting from the second element.
Step 3: Compare and Update the Minimum Value:
- For each element, compare ans with the current value stored in the nums[i]. If the nums[i] is smaller, update the ans with this new value.
Step 4: Return the Minimum Value:
- After completing the iteration, return the value stored in the ans variable.
Find Minimum in Rotated Sorted Array II Solution
Find Minimum in Rotated Sorted Array II Solution in C++
class Solution {
public:
// Function to find the minimum element in a sorted, rotated array
int findMin(vector<int>& nums) {
// Initialize the variable ans with the first element of the array
int ans = nums[0];
// Get the size of the array
int n = nums.size();
// Iterate through the array starting from the second element
for(int i = 1; i < n; ++i) {
// Compare and update the ans variable
ans = min(ans, nums[i]);
}
// Return the minimum value
return ans;
}
};Find Minimum in Rotated Sorted Array II Solution in Java
class Solution {
// Function to find the minimum element in a sorted, rotated array
public int findMin(int[] nums) {
// Initialize the variable ans with the first element of the array
int ans = nums[0];
// Get the size of the array
int n = nums.length;
// Iterate through the array starting from the second element
for (int i = 1; i < n; ++i) {
// Compare and update the ans variable
ans = Math.min(ans, nums[i]);
}
// Return the minimum value
return ans;
}
}Find Minimum in Rotated Sorted Array II Solution in Python
class Solution:
# Function to find the minimum element in a sorted, rotated array
def findMin(self, nums: list[int]) -> int:
# Initialize the variable ans with the first element of the array
ans = nums[0]
# Iterate through the array starting from the second element
for i in range(1, len(nums)):
# Compare and update the ans variable
ans = min(ans, nums[i])
# Return the minimum value
return ansFind Minimum in Rotated Sorted Array II Solution in Javascript
/**
* @param {number[]} nums
* @return {number}
*/
var findMin = function(nums) {
// Initialize the variable ans with the first element of the array
let ans = nums[0];
// Iterate through the array starting from the second element
for (let i = 1; i < nums.length; ++i) {
// Compare and update the ans variable
ans = Math.min(ans, nums[i]);
}
// Return the minimum value
return ans;
};Find Minimum in Rotated Sorted Array II Complexity Analysis
Time Complexity: O(n)
Initialization of the Minimum Variable:
- Initializing the variable ans with the first element of the array takes constant time, O(1).
Getting the Size of the Array:
- Accessing the size of the array also takes constant time, O(1).
Iteration Through the Array:
- The loop runs from the second element (index 1) to the last element (index n-1). Since the array has n elements, this loop iterates n-1 times. This process takes linear time. O(n)
- Each iteration involves comparing the current element with the ans variable and potentially updating ans. These operations within the loop take constant time, O(1).
Returning the Result:
Returning the value of ans after completing the iteration takes constant time, O(1).
Hence total time complexity is O(n)
Space Complexity: O(1)
Auxiliary Space Complexity:
- Auxiliary space refers to the extra space or temporary space used by the algorithm during its execution, excluding the input data.
- In the provided code, we use a single variable ans to store the minimum element found during iteration. This variable takes constant space, O(1).
- The loop control variables (i and n) also take constant space, O(1).
Therefore, the auxiliary space complexity of the code is O(1).
Total Space Complexity:
- Total space complexity includes both the space used by the input data and the auxiliary space.
- The input array nums is given as input to the function, which takes up space O(n), where n is the number of elements in the array.
Total space complexity = Space used by input data + Auxiliary space complexity = O(n) + O(1) = O(n)
Is the brute force solution efficient?
A brute force solution with a time complexity of O(N) is well-suited to the given constraints. It comfortably runs within the time limits of most competitive programming environments, typically allowing around 1-2 seconds for execution.
Even when multiple test cases are involved, resulting in a total of up to 10⁸ operations, this complexity remains optimal. Therefore, the solution ensures efficient execution without risking a Time Limit Exceeded (TLE) error.
However, we did not make use of the constraints that the given array is sorted and rotated. Let's try to optimize the solution and see how we can make use of it.
Optimal Approach
Intuition:
We iterated through every index using the brute force approach to find the minimum value in the array.
To reduce the complexity from O(n), we need to avoid iterating through every index of the array. Instead, we should focus on strategically narrowing down the search space to a specific part of the array where we are confident the minimum element resides.
Before proceeding, it’s recommended to review the article linked below, as it addresses the exact same problem but with a simpler scenario where no duplicates exist in the rotated sorted array. The approach discussed in the article forms the foundation for solving this problem. However, since this array includes duplicates, a slight modification to the strategy is required to account for duplicate values effectively.
Here also, we will start by picking some arbitrary index i from the array. It will either lie in the first part (from index 0 to index pivot-1) or the second part (from pivot to n-1). Here, pivot is the index of the minimum element in the array.
Let's focus on the important part here. For now, forget that the array contains duplicates. Then how would you solve the problem?. This is mentioned in detail in the article mentioned above. Let's revise it, if you have already read it.
To start with, we need to decide if the minimum value lies to the left of index i or to the right of index i. If we can determine this, we can eliminate the other side, keeping things efficient.
To determine whether the selected index is part of the first part or the second part of a sorted rotated array, we can use an important observation: all elements in the second part are smaller than all elements in the first part.
Initially, we focus on the last element of the search space. By comparing the value at the selected index with the previous element of the search space, we can determine which direction to proceed in our search.
If the selected index's value is smaller than or equal to the last element, it indicates that the index lies in the second half of the array. Conversely, if the selected index's value is greater than the last element, it means the index lies in the first half.
This comparison allows us to adjust our search space efficiently: if the index lies in the first half, we continue searching to the right, and if it lies in the second half, we search to the left.
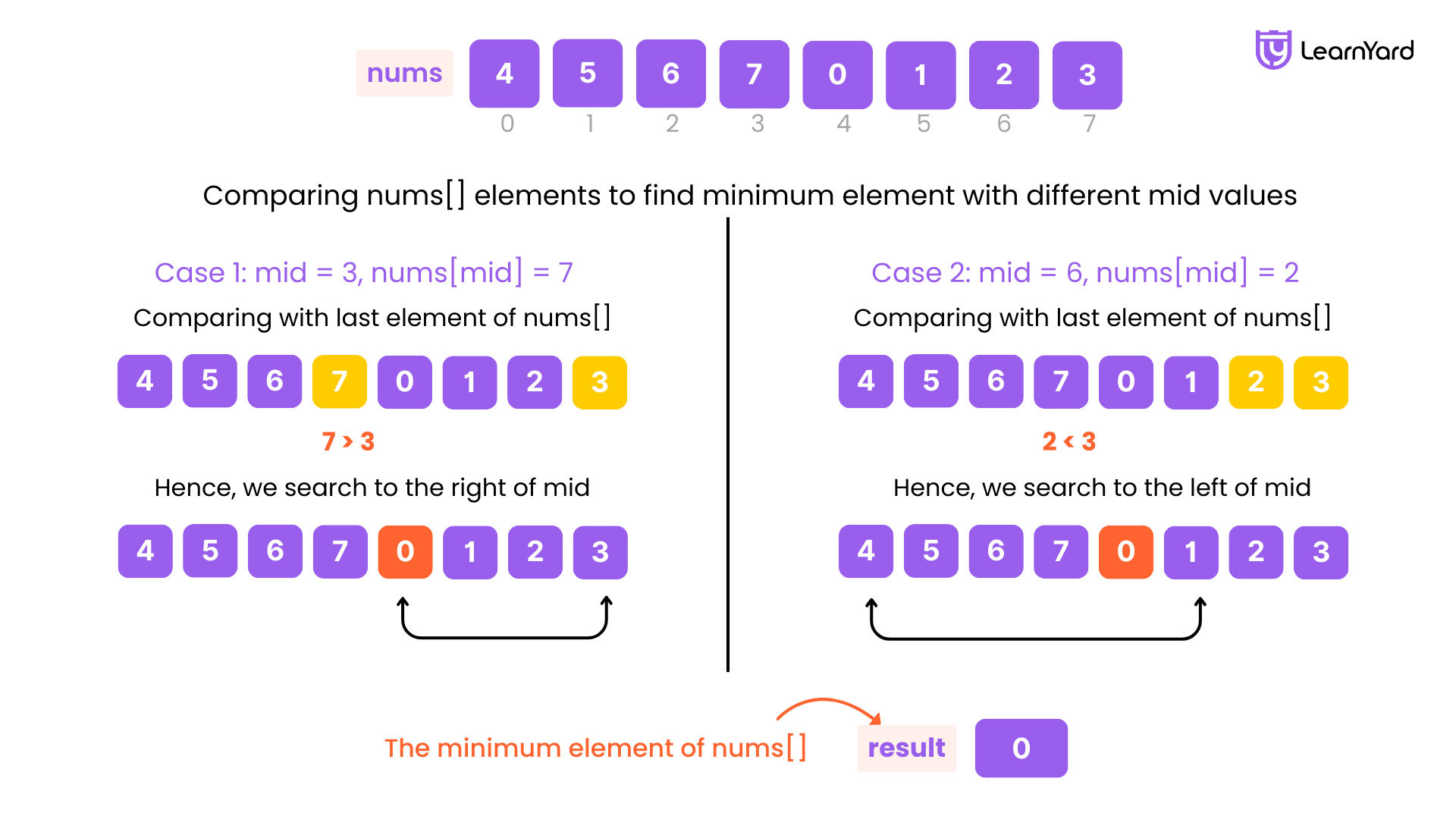
Example
nums : [4, 5, 6, 7, 0, 1, 2, 3]
Let’s choose an index i = 3 (value = 7).
We compare the value at index i (7) with the last element of the search space (3):
- Since 7 > 3, it indicates that the index i = 3 lies in the first half of the array.
- Hence, we search to the right of index i (narrowing our search to the part where the minimum could be).
Now, let’s choose a different index: Index i = 6 (value = 2).
We compare the value at index i (2) with the last element of the search space (3):
- Since 2 < 3, it indicates that the index i = 6 lies in the second half of the array.
- Hence, we search to the left of index i.
This strategy ensures we efficiently reduce the search space while navigating towards the minimum element.
Initially, we define two pointers, low and high, representing our search space. Then we will run our algorithm until our search space reduces to one element (low == high) or becomes invalid (low > high).
For every iteration, we choose our arbitrary index i, which is nothing but the middle index of the array. As it is most efficient. You can clearly see that deciding if the minimum element lies on any side of the middle element will help us to choose that side and reject the other side. Meaning our search space will be reduced to half of the previous search space.
This process of narrowing down the search space in half until we find our answer is called binary search.
We now know what to do if there are no duplicates. Now let's see what we can do with the duplicates...
In a rotated, sorted array with duplicates, repeated values can complicate the search process, especially when trying to determine which part of the array to focus on next. This ambiguity arises when the values at the low, mid, and high pointers are the same, making it unclear whether the target lies in the left or right half of the array.
If the value at the low pointer is greater than the value at mid, while the value at high is equal to the value at mid, we can confidently look at the left side of mid. This is because the minimum element must either lie at mid itself or somewhere further to the left.
However, if all three values, low, mid, and high, are the same, this introduces complete ambiguity, as no clear direction can be deduced from the comparison. To handle this scenario, we simply move the low pointer up or the high pointer down, effectively eliminating the duplicate values one by one.
How does this help?
Moving the low pointer up (low++) and the high pointer down (high--) helps us skip over the duplicate values. This action narrows our search space, making it smaller and easier to manage. It’s like cutting away the excess, so we only focus on the part of the array that’s more likely to contain our target.
But what if, doing this again, we find that all 3 (numbers at low, mid and high) are the same? No problem, we again increment low and decrement high, ensuring that the search space is constantly narrowing down. This strategy helps you find the minimum value in the rotated sorted array, even with duplicates.
Animation showing How Optimal Approach Works
Find Minimum in Rotated Sorted Array II Example
Input: nums = [4, 9, 11, 2, 2, 4]
Output: 2
Explanation: The minimum element in nums is 2.
Initial State:
- nums = [4, 9, 11, 2, 4, 4]
- low = 0, high = 5
- n = 6 (size of array)
First Iteration:
- mid = (0 + 5) / 2 = 2
- nums[mid] = 11, nums[low] = 4, nums[high] = 4
Condition Check:
- nums[mid] == nums[low] && nums[mid] == nums[high] (11 == 4 && 11 == 4) → False
- nums[mid] > nums[high] (11 > 4) → True
Action: Set low = mid + 1 = 3
Second Iteration:
- low = 3, high = 5
- mid = (3 + 5) / 2 = 4
- nums[mid] = 4, nums[low] = 2, nums[high] = 4
Condition Check:
- nums[mid] == nums[low] && nums[mid] == nums[high] (4 == 2 && 4 == 4) → False
- nums[mid] > nums[high] (4 > 4) → False
- Otherwise, Action: Set high = mid = 4
Third Iteration:
- low = 3, high = 4
- mid = (3 + 4) / 2 = 3
- nums[mid] = 2, nums[low] = 2, nums[high] = 4
Condition Check:
- nums[mid] == nums[low] && nums[mid] == nums[high] (2 == 2 && 2 == 4) → False
- nums[mid] > nums[high] (2 > 4) → False
- Otherwise, Action: Set high = mid = 3
Final State:
- low = 3, high = 3
- Loop exits because low >= high.
Return: nums[low] = nums[3] = 2
Find Minimum in Rotated Sorted Array II Algorithm
Step 1: Initialize pointers:
- Start with two pointers: low = 0 and high = n - 1, where n is the size of the array.
Step 2: Iterate using a loop:
- Use a while loop that runs until low < high.
Step 3: Calculate the middle index:
- Compute the middle index as mid = (low + high) / 2.
Step 4: Handle the case with duplicate values:
- Check if nums[low] == nums[mid] && nums[mid] == nums[high].
- If true, increment low and decrement high to reduce the search space and eliminate ambiguity.
Step 5: Adjust search space based on array rotation:
- If nums[mid] > nums[high], this means the minimum is in the right half, so setlow = mid + 1.
- Otherwise, the minimum is in the left half or at mid, so set high = mid.
Step 6: Exit condition:
- The loop exits when low == high, meaning the search space has been reduced to a single element.
Step 7: Return the result:
- The minimum element will be at nums[low].
Find Minimum in Rotated Sorted Array II Leetcode Solution in All Languages
Find Minimum in Rotated Sorted Array II Leetcode Solution in C++
class Solution {
public:
// Function to find the minimum element in a rotated sorted array with duplicates
int findMin(vector<int>& nums) {
// Get the size of the array
int n = nums.size();
// Initialize pointers for the start and end of the array
int low = 0, high = n - 1;
// While the search space has more than one element
while (low < high) {
// Calculate the middle index of the current search space
int mid = (low + high) / 2;
// If all three elements (low, mid, high) are equal
if (nums[mid] == nums[low] && nums[mid] == nums[high]) {
// Move the low pointer to the right to eliminate duplicates
low++;
// Move the high pointer to the left to eliminate duplicates
high--;
}
// If the middle element is greater than the element at high, the minimum is in the right half
else if (nums[mid] > nums[high]) {
// Move the low pointer to the right of mid to search the right half
low = mid + 1;
}
// Otherwise, the minimum is in the left half or at mid
else {
// Move the high pointer to mid to search the left half
high = mid;
}
}
// Return the element at the low pointer, which is the minimum element
return nums[low];
}
};Find Minimum in Rotated Sorted Array II Leetcode Solution in Java
class Solution {
// Function to find the minimum element in a rotated sorted array with duplicates
public int findMin(int[] nums) {
// Initialize pointers for the start and end of the array
int low = 0, high = nums.length - 1;
// While the search space has more than one element
while (low < high) {
// Calculate the middle index of the current search space
int mid = low + (high - low) / 2;
// If all three elements (low, mid, high) are equal
if (nums[mid] == nums[low] && nums[mid] == nums[high]) {
// Move the low pointer to the right to eliminate duplicates
low++;
// Move the high pointer to the left to eliminate duplicates
high--;
}
// If the middle element is greater than the element at high, the minimum is in the right half
else if (nums[mid] > nums[high]) {
// Move the low pointer to the right of mid to search the right half
low = mid + 1;
}
// Otherwise, the minimum is in the left half or at mid
else {
// Move the high pointer to mid to search the left half
high = mid;
}
}
// Return the element at the low pointer, which is the minimum element
return nums[low];
}
}Find Minimum in Rotated Sorted Array II Leetcode Solution in Python
class Solution:
# Function to find the minimum element in a rotated sorted array with duplicates
def findMin(self, nums: List[int]) -> int:
# Initialize pointers for the start and end of the array
low, high = 0, len(nums) - 1
# While the search space has more than one element
while low < high:
# Calculate the middle index of the current search space
mid = (low + high) // 2
# If all three elements (low, mid, high) are equal
if nums[mid] == nums[low] and nums[mid] == nums[high]:
# Move the low pointer to the right to eliminate duplicates
low += 1
# Move the high pointer to the left to eliminate duplicates
high -= 1
# If the middle element is greater than the element at high, the minimum is in the right half
elif nums[mid] > nums[high]:
# Move the low pointer to the right of mid to search the right half
low = mid + 1
# Otherwise, the minimum is in the left half or at mid
else:
# Move the high pointer to mid to search the left half
high = mid
# Return the element at the low pointer, which is the minimum element
return nums[low] Find Minimum in Rotated Sorted Array II Leetcode Solution in Javascript
/**
* @param {number[]} nums
* @return {number}
*/
var findMin = function(nums) {
// Initialize pointers for the start and end of the array
let low = 0, high = nums.length - 1;
// While the search space has more than one element
while (low < high) {
// Calculate the middle index of the current search space
let mid = Math.floor((low + high) / 2);
// If all three elements (low, mid, high) are equal
if (nums[mid] === nums[low] && nums[mid] === nums[high]) {
// Move the low pointer to the right to eliminate duplicates
low++;
// Move the high pointer to the left to eliminate duplicates
high--;
}
// If the middle element is greater than the element at high, the minimum is in the right half
else if (nums[mid] > nums[high]) {
// Move the low pointer to the right of mid to search the right half
low = mid + 1;
}
// Otherwise, the minimum is in the left half or at mid
else {
// Move the high pointer to mid to search the left half
high = mid;
}
}
// Return the element at the low pointer, which is the minimum element
return nums[low];
};Find Minimum in Rotated Sorted Array II Complexity Analysis
Time Complexity: O(log n)
Initialization:
- Initializing n (size of nums), low and high takes constant time operations O(1).
While loop
- Each time, the loop either reduces the search space by half (in the case of non-duplicate comparisons), or adjusts low and high when duplicates are found.
n --> n/2 --> n/4 --> n/8 .... 1. - Therefore, the loop runs for at most O(log N) iterations, as each iteration reduces the search space, even though handling duplicates might reduce it more slowly.
Calculating mid and if conditions:
- All the operations inside the while loop which includes calculating mid, checking if condition takes constant time operation O(1).
Hence, the overall time complexity of the algorithm is O(log n)
Space Complexity: O(1)
Auxiliary Space Complexity:
Auxiliary space refers to the extra space used by the algorithm, excluding the space required for the input.
- The only extra space used in the code is for the three integer variables: low, high, and mid, each of which takes O(1) space.
- Since no additional data structures are used (like arrays, lists, or stacks), the auxiliary space complexity is O(1).
Total Space Complexity:
Total space complexity refers to the overall memory used by the program, including both the input size and any additional memory used by the algorithm.
- Input Size: The space used by the input nums (the array) is O(N), where N is the number of elements in the array. This is part of the total space complexity since the input array needs to be stored in memory.
- Auxiliary Space: The space used by the algorithm itself (excluding the input) is O(1).
Thus, the total space complexity is O(N), accounting for the input array.
Similar Problems
Now we have successfully tackled this problem, let's try these similar problems:-
There is an integer array nums sorted in non-decreasing order (not necessarily with distinct values).
Before being passed to your function, nums is rotated at an unknown pivot index k (0 <= k < nums.length) such that the resulting array is [nums[k], nums[k+1], ..., nums[n-1], nums[0], nums[1], ..., nums[k-1]] (0-indexed). For example, [0,1,2,4,4,4,5,6,6,7] might be rotated at pivot index 5 and become [4,5,6,6,7,0,1,2,4,4].
Given the array nums after the rotation and an integer target, return true if target is in nums, or false if it is not in nums.
You must decrease the overall operation steps as much as possible.
Given an integer array nums, find a
subarray that has the largest product, and return the product.
The test cases are generated so that the answer will fit in a 32-bit integer.