Find in Mountain Array Solution In C++/Java/Python/JS
Problem Description:
(This problem is an interactive problem.)
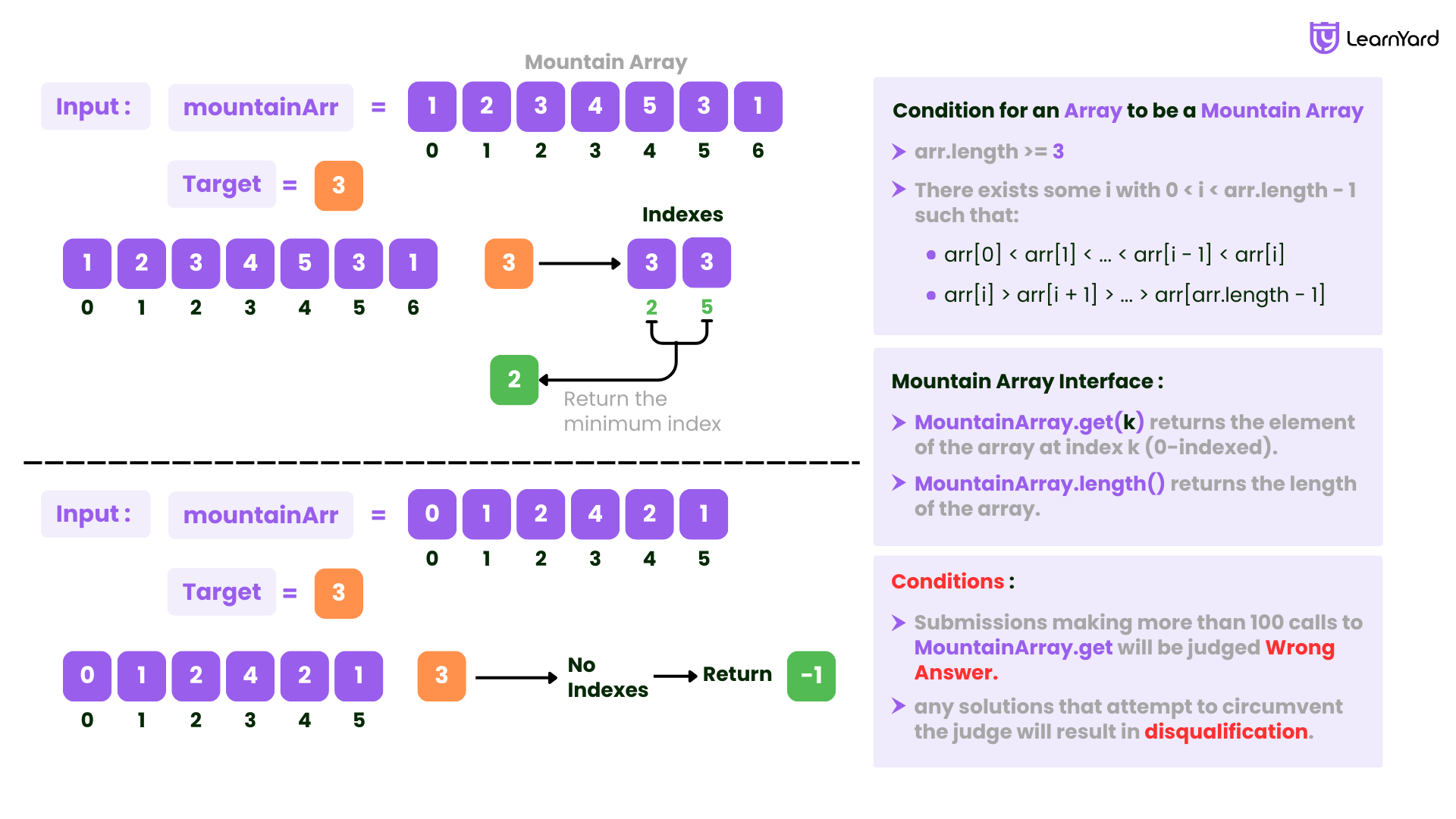
You may recall that an array arr is a mountain array if and only if:
- arr.length >= 3
- There exists some i with 0 < i < arr.length - 1 such that:
- arr[0] < arr[1] < ... < arr[i - 1] < arr[i]
- arr[i] > arr[i + 1] > ... > arr[arr.length - 1]
Given a mountain array mountainArr, return the minimum index such that mountainArr.get(index) == target. If such an index does not exist, return -1.
You cannot access the mountain array directly. You may only access the array using a MountainArray interface:
- MountainArray.get(k) returns the element of the array at index k (0-indexed).
- MountainArray.length() returns the length of the array.
Submissions making more than 100 calls to MountainArray.get will be judged Wrong Answer. Also, any solutions that attempt to circumvent the judge will result in disqualification.
Examples:
Input: mountainArr = [1,2,3,4,5,3,1], target = 3
Output: 2
Explanation: 3 exists in the array, at index=2 and index=5. Return the minimum index, which is 2.
Input: mountainArr = [0,1,2,4,2,1], target = 3
Output: -1
Explanation: 3 does not exist in the array, so we return -1.
Constraints:
- 3 <= mountainArr.length() <= 104
- 0 <= target <= 109
- 0 <= mountainArr.get(index) <= 109
In this problem, we are given a special type of array called a mountain array, which first increases to a peak and then decreases. Our goal is to search for a specific target value within this array and return its index if found.
If the target appears multiple times, we return the smallest index among them. If the target is not present, we return -1.
How would you approach this problem? Let's check out.
Brute Force Approach
Intuition:
The first question that arises is why we don't check every index and return it once we reach the target index. Isn't it straightforward?. Let's see how exactly we can do this.
We iterate through the entire array from left to right, checking each index to see if it matches the target value. As soon as we find the target, we simply return the index of the target. Because by default we will land on the first occurrence of the target as we are moving from left to right (from index 0 to n-1).
However, if we don't find the target at any index of the array, or we reach the end of the array without finding the target, we return -1.
Find in Mountain Array Example
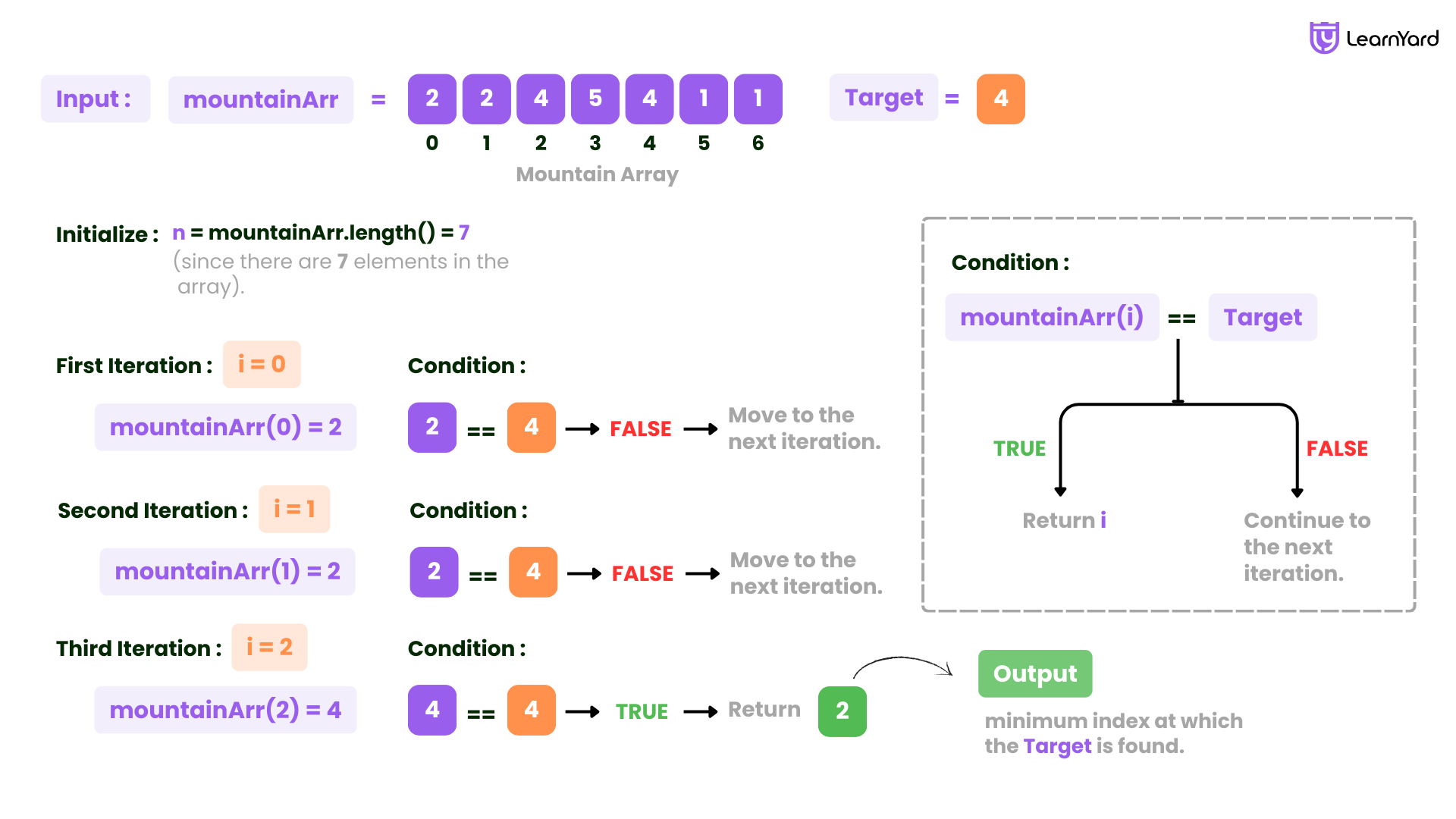
Input: mountainArr = [2, 2, 4, 5, 4, 1, 1], target = 4
Output: 2
Explanation: 4 exists in the array, at index=2 and index=4. Return the minimum index, which is 2.
Initialize:
- n = mountainArr.length()
- n = 7 (since there are 7 elements in the array).
First Iteration (i = 0):
- mountainArr.get(0) returns 2.
- Check: 2 == 4? No.
- Continue to the next iteration.
Second Iteration (i = 1):
- mountainArr.get(1) returns 2.
- Check: 2 == 4? No.
- Continue to the next iteration.
Third Iteration (i = 2):
- mountainArr.get(2) returns 4.
- Check: 4 == 4? Yes.
- The condition is true, so return the index 2.
Result:
- The function finds the target value 4 at index 2 and immediately returns 2.
Find in Mountain Array Algorithm
Step 1: Initialize the size of the array
- Start by getting the size of the mountain array using mountainArr.length(). This gives us the total number of elements in the array, which we store in the variable n.
Step 2: Iterate Through the Mountain Array
- Use a loop to go through each element in the mountain array from the start to the end.
- The loop will check every element one by one.
Step 3: Compare and Update
- For each element, compare the current element (mountainArr.get(i)) with the target.
- If they match, immediately return the index i where the target was found.
Step 4: Return the Result
- If the loop completes and the target is not found, return -1 to indicate that the target does not exist in the mountain array.
Find in Mountain Array Solution in all languages
Find in Mountain Array Solution in C++
/**
* // This is the MountainArray's API interface.
* // You should not implement it, or speculate about its implementation
* class MountainArray {
* public:
* int get(int index);
* int length();
* };
*/
class Solution {
public:
int findInMountainArray(int target, MountainArray &mountainArr) {
// Get the size of the mountain array
int n = mountainArr.length();
// Iterate through the entire array
for (int i = 0; i < n; ++i) {
// Check if the current element matches the target
if (mountainArr.get(i) == target) {
// Return the index of the first occurrence
return i;
}
}
// Target not found
return -1;
}
};Find in Mountain Array Solution in Java
/**
* // This is MountainArray's API interface.
* // You should not implement it, or speculate about its implementation
* interface MountainArray {
* public int get(int index) {}
* public int length() {}
* }
*/
class Solution {
public int findInMountainArray(int target, MountainArray mountainArr) {
// Get the size of the mountain array
int n = mountainArr.length();
// Iterate through the entire array
for (int i = 0; i < n; ++i) {
// Check if the current element matches the target
if (mountainArr.get(i) == target) {
// Return the index of the first occurrence
return i;
}
}
// Target not found
return -1;
}
}Find in Mountain Array Solution in Python
# """
# This is MountainArray's API interface.
# You should not implement it, or speculate about its implementation
# """
#class MountainArray:
# def get(self, index: int) -> int:
# def length(self) -> int:
class Solution:
def findInMountainArray(self, target: int, mountainArr: 'MountainArray') -> int:
# Get the size of the mountain array by calling the length method
n = mountainArr.length()
# Iterate through the entire array using a loop
for i in range(n):
# Check if the current element matches the target
if mountainArr.get(i) == target:
# Return the index of the first occurrence of the target
return i
# If target is not found, return -1
return -1Find in Mountain Array Solution in Javascript
/**
* // This is the MountainArray's API interface.
* // You should not implement it, or speculate about its implementation
* function MountainArray() {
* @param {number} index
* @return {number}
* this.get = function(index) {
* ...
* };
*
* @return {number}
* this.length = function() {
* ...
* };
* };
*/
/**
* @param {number} target
* @param {MountainArray} mountainArr
* @return {number}
*/
var findInMountainArray = function(target, mountainArr) {
// Get the size of the mountain array
let n = mountainArr.length();
// Iterate through the entire array
for (let i = 0; i < n; i++) {
// Check if the current element matches the target
if (mountainArr.get(i) === target) {
// Return the index of the first occurrence
return i;
}
}
// Target not found
return -1;
};Find in Mountain Array Complexity Analysis
Time Complexity: O(n)
Initialization:
- This operation simply returns the length of the array, which is a constant-time operation, i.e., O(1).
The for loop:
- The loop iterates over all the elements of the array, which means it runs n times, where n is the length of the mountain array.
- In each iteration, it calls mountainArr.get(i) to get the element at index i. The get(i) method is assumed to be a constant-time operation, i.e., O(1).
- So, the loop's time complexity is O(n), where n is the number of elements in the array.
Returning the result:
- The return operation at the end is done in constant time, i.e., O(1).
Hence, the overall time complexity is O(n)
Space Complexity: O(1)
Auxiliary Space Complexity:
The auxiliary space complexity refers to the extra space or memory used by the algorithm, excluding the space used by the input.
- Auxiliary Space:
The algorithm uses only a few variables, such as n (the length of the array), and it does not use any data structures like arrays, lists, or recursion. The for loop does not allocate additional memory.
Thus, the auxiliary space complexity is: O(1)
Total Space Complexity:
The total space complexity includes the space used by both the input and any additional space needed by the algorithm.
- Input space:
The input consists of the mountainArr (which is a MountainArray object) and the target value. Time complexity for input is O(n) - Space used by variables in the function:
The only additional space used in the function is for the variable n, which stores the length of the array. This requires constant space O(1).
Since no additional space needed for data structures are used the total space complexity is O(n) taking input space into account.
Is the brute force solution efficient?
For n ≤ 10⁴, our solution has a time complexity of O(n). This is well within the time limits of most competitive programming environments, which typically allow around 1-2 seconds for execution.
But if you read the last two lines of the problem statement it says that we cannot make more than 100 calls. n <= 104. In the worst case we are making 104 calls. Hence our solution won't get accepted. We need to optimize the solution.
We have to figure out a way to make less than 100 calls to find the first index of the target. Let's see how to do this...
Optimal Approach
Intuition:
We now know that we can't afford a linear time complexity. That specifically means that we can't go over every index of the array to find the target. Instead, we need to select a specific part of the array where we are confident that we can find our target value.
The array we are given is a mountain array, which has a unique property: it first increases from index 0 to the peak, and then decreases from the peak to the last index (n-1). The index of the greatest element is called the peak. This property of the mountain array gives us a crucial insight that we can use to optimise our solution.
Imagine you are on a hike along a mountain trail. The path starts at the base, steadily climbs up to the peak, and then descends down the other side. Along the way, you are looking for a specific signpost that has an important message for you. However, instead of searching step by step, you want to find it as efficiently as possible.
The target we are trying to find will either be at the peak, to the left of the peak (where the slope is increasing), or to the right of the peak (where the slope is decreasing). This insight allows us to split the array into two parts: the left part, where the values are increasing, and the right part, where the values are decreasing.
Example:
nums = [2, 4, 5, 5, 7, 4, 4, 3]
The nums can be divided into two parts:
- left part = [2, 4, 5, 5, 7] (every other value is greater than or equal)
- right part = [4, 4, 3] (every other value is smaller or equal)
- left part + right part = whole array
- [2, 4, 5, 5, 7] + [4, 4, 3] = [2, 4, 5, 5, 7, 4, 4, 3]
The peak can come in either of the two parts.
Given that the array is a mountain array, we can observe that the elements in the left part of the array are continuously increasing until the peak value, meaning the left part is sorted in ascending order.
On the other hand, the right part of the array has values that decrease from the peak index to the end, indicating that the right part is sorted in descending order.
By dividing the array into two parts, we get two sorted arrays (the uphill part of the mountain and the downhill part of the mountain), which makes it easier to find the peak.
To understand how this works, it is highly recommended that you first read the following article on finding the peak in a mountain array, as this concept will be directly applied to split the array into two parts.
At this point, we know how to find the peak index in a mountain array. This means we have divided the whole array into two search spaces from 0 to peak (uphill) and from peak+1 to n-1 (down hill).
Now the target index can lie in either of the two parts or both parts. As we are supposed to return the minimum index, we will first focus on the left or the first part (uphill), which consists of the smaller index from 0 to the peak.
We will perform a normal binary search to find the target. If you don't know what binary search is. Please read the following article.
Step 1: Finding the First Index in the Left Part (uphill)
Imagine you’re hiking up the mountain and looking for a signpost. Since the path is in increasing order, if you pass a certain point and still haven’t found the signpost, you never need to go back—it must be further ahead or doesn’t exist.
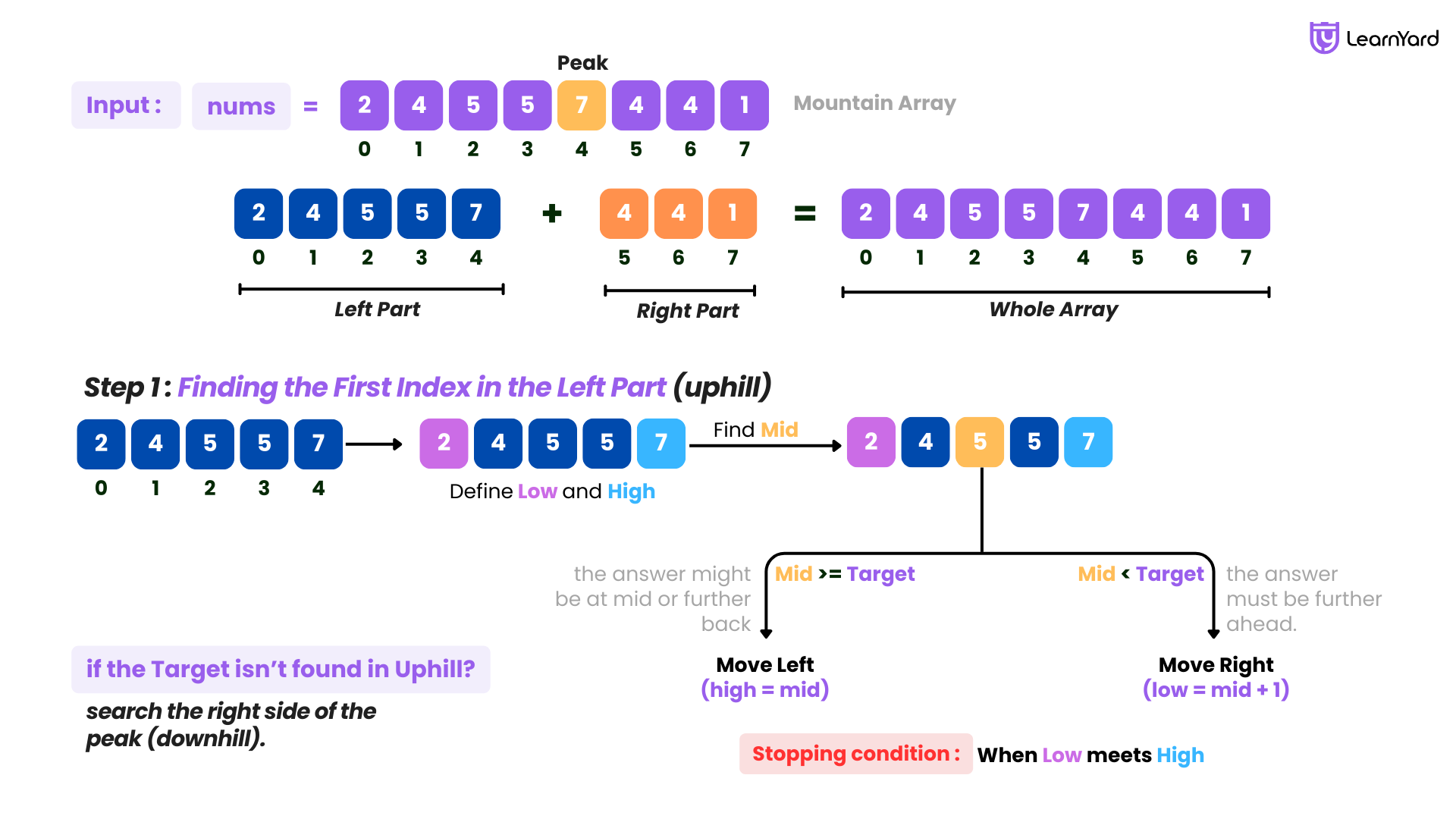
How to Search Efficiently?
- Define the search area → Start at the base of the mountain (low = 0) and go up to the peak (high = peak).
- Look at the middle point (mid):
- If mid is smaller than the signpost number, it must be further ahead. Move right (low = mid + 1).
- If mid is equal to or greater than the signpost number, the answer might be at mid or further back. Move left (high = mid).
- Stopping condition → When low meets high, that is the first occurrence of the target in the left part.
What if the signpost isn’t found?
If we reach a point where the value at the index low is not equal to the signpost number, we need to search the right side of the peak (downhill).
Step 2: Finding the First Index in the Right Part (downhill)
Now, imagine you’ve reached the peak of the mountain but didn’t find the signpost on the way up. What should you do? Start searching on the downhill path. However, the rules change slightly because this part of the path is sorted in descending order, meaning the bigger numbers come first.
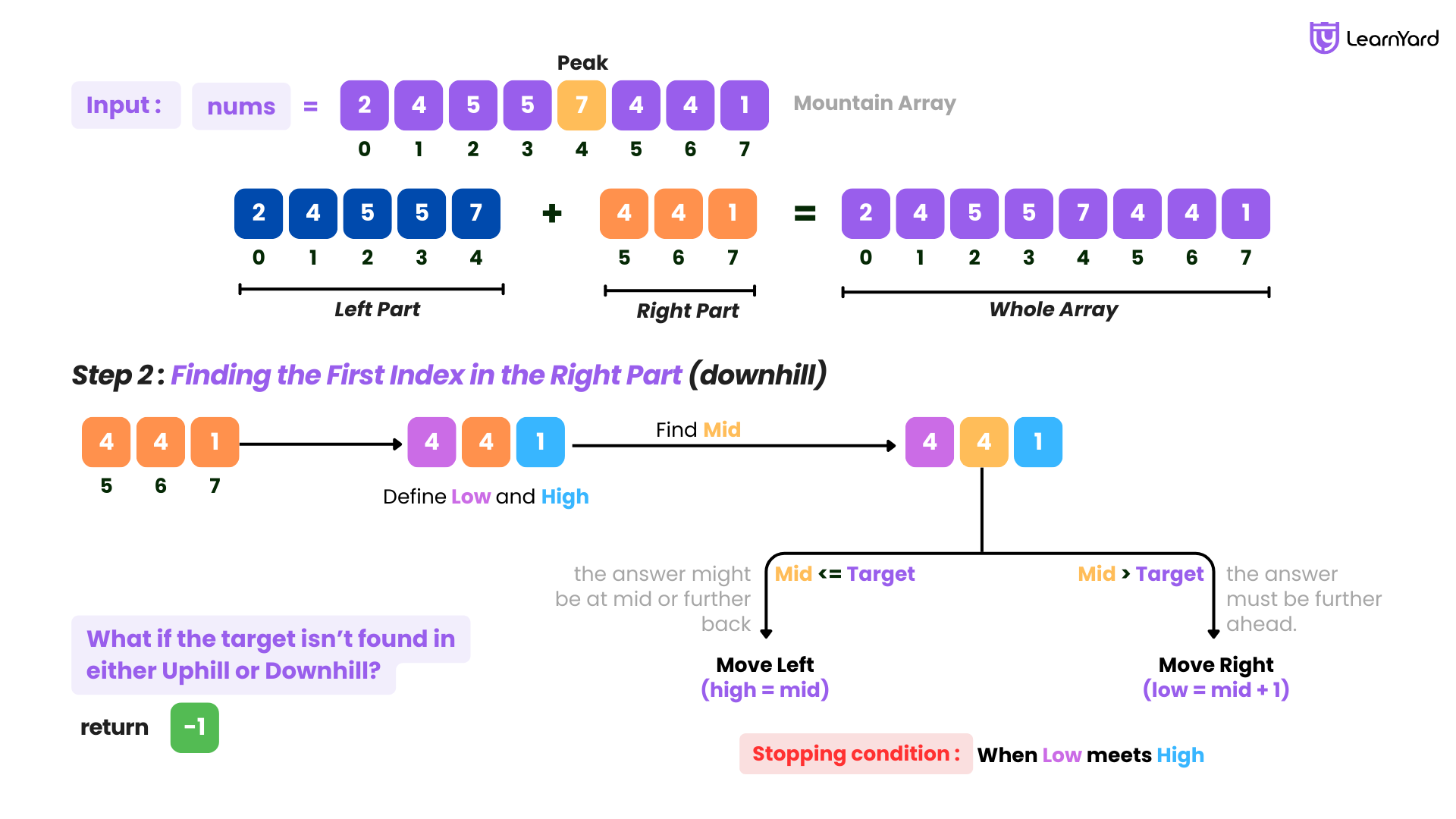
How to Search Efficiently?
- Define the search area → Start at the peak (low = peak) and go down to the end of the array (high = n-1).
- Look at the middle point (mid):
- If mid is greater than the signpost number, it must be further ahead down the slope. Move right (low = mid + 1).
- If mid is equal to or smaller than the signpost number, the answer might be at mid or further back. Move left (high = mid).
- Stopping condition → When low meets high, that is the first occurrence of the target in the right part.
If both of these searches terminated without returning a valid index, then we can conclude that the array doesn't have even a single occurrence of the target. So, we return -1.
Animation showing How Optimal Approach Works.
Find in Mountain Array Example
Input: mountainArr = [2, 2, 4, 5, 4, 1, 1], target = 4
Output: 2
Explanation: 4 exists in the array, at index=2 and index=4. Return the minimum index, which is 2.
Initial Setup
- mountainArr = [2, 2, 4, 5, 4, 1, 1]
- target = 4
Step 1: Finding the Peak Element find_peak function
- We start by setting low = 0 and high = 6 (the length of the array minus 1).
- In the first iteration, mid = (0 + 6) / 2 = 3:
- arr.get(3) = 5 and arr.get(4) = 4, since arr.get(mid) > arr.get(mid+1), we update high = mid = 3.
- In the second iteration, mid = (0 + 3) / 2 = 1:
- arr.get(1) = 2 and arr.get(2) = 4, since arr.get(mid) <= arr.get(mid+1), we update low = mid + 1 = 2.
- In the third iteration, mid = (2 + 3) / 2 = 2:
- arr.get(2) = 4 and arr.get(3) = 5, since arr.get(mid) <= arr.get(mid+1), we update low = mid + 1 = 3.
- Now, low == high, so the peak element is at index 3. Therefore, peak = 3.
Step 2: Binary Search on the Left of the Peak
We now perform a binary search on the left half of the array, from index 0 to peak = 3.
- We initialize low = 0 and high = 3.
- In the first iteration, mid = (0 + 3) / 2 = 1:
- arr.get(1) = 2, which is less than target = 4, so we update low = mid + 1 = 2.
- In the second iteration, mid = (2 + 3) / 2 = 2:
- arr.get(2) = 4, which is equal to the target, so we return the index 2.
Final Result:
- The target 4 is found at index 2, so the final result is 2.
Find in Mountain Array Algorithm
Step 1: Finding the Peak Element
- Initialize low = 0 and high = arr.length() - 1.
- Check boundary conditions:
- If arr.get(arr.length() - 1) > arr.get(arr.length() - 2), return arr.length() - 1.
- If arr.get(0) > arr.get(1), return 0.
- Perform binary search:
- While low < high:
- Calculate mid = (low + high) / 2.
- If arr.get(mid) < arr.get(mid + 1), move low = mid + 1.
- Otherwise, move high = mid.
- Return low as the peak index.
Step 2: Binary Search on Left Half (Increasing Part)
- Initialize low = 0 and high = peak.
- Perform binary search:
- While low < high:
- Calculate mid = (low + high) / 2.
- If arr.get(mid) < target, move low = mid + 1.
- Otherwise, move high = mid.
- If arr.get(low) == target, return low.
Step 3: Binary Search on Right Half (Decreasing Part)
- Initialize low = peak and high = arr.length() - 1.
- Perform binary search:
- While low < high:
- Calculate mid = (low + high) / 2.
- If arr.get(mid) > target, move low = mid + 1.
- Otherwise, move high = mid.
- If arr.get(low) == target, return high.
Step 4: Return -1
- If the target is not found in either part, return -1.
Find in Mountain Array Leetcode Solution in C++
C++
/**
* // This is the MountainArray's API interface.
* // You should not implement it, or speculate about its implementation
* class MountainArray {
* public:
* int get(int index);
* int length();
* };
*/
class Solution {
public:
// Function to find the peak element in the mountain array
int find_peak(MountainArray &arr) {
// Initialize the low and high pointers for binary search
int low = 0;
int high = arr.length() - 1;
// Perform binary search to find the peak element
while (low < high) { // Keep searching until low and high pointers converge
// Calculate the mid index
int mid = (low + high) / 2;
// If the middle element is less than or equal to the next element,
// the peak must be on the right side of mid
if (arr.get(mid) <= arr.get(mid + 1)) {
// Move the low pointer to mid + 1 if peak is to the right
low = mid + 1;
} else {
// Otherwise, move the high pointer to mid
high = mid;
}
}
// Return the index of the peak element
return low;
}
// Function to find the target in the mountain array
int findInMountainArray(int target, MountainArray &arr) {
// Step 1: Find the peak element
int peak = find_peak(arr); // Get the index of the peak element
// Step 2: Perform binary search on the left side of the peak
int low = 0, high = peak; // Initialize low and high for left side search
while (low < high) { // Continue the search until low and high converge
// Calculate the mid index
int mid = (low + high) / 2;
// If the middle element is smaller than the target,
// move the low pointer to mid + 1
if (arr.get(mid) < target) {
low = mid + 1;
} else {
// Otherwise, move the high pointer to mid
high = mid;
}
}
// After the loop, check if the target is found at the low index
if (arr.get(low) == target) return low; // Return the index if the target is found
// Step 3: Perform binary search on the right side of the peak
low = peak; // Set low to the peak index
high = arr.length() - 1; // Set high to the last index of the array
while (low < high) { // Continue searching until low and high converge
// Calculate the mid index
int mid = (low + high) / 2;
// If the middle element is greater than the target,
// move the low pointer to mid + 1
if (arr.get(mid) > target) {
low = mid + 1;
} else {
// Otherwise, move the high pointer to mid
high = mid;
}
}
// After the loop, check if the target is found at the high index
if (arr.get(low) == target) return high; // Return the index if the target is found
// If the target is not found, return -1
return -1;
}
};
Find in Mountain Array Leetcode Solution in Java
/**
* // This is MountainArray's API interface.
* // You should not implement it, or speculate about its implementation
* interface MountainArray {
* public int get(int index) {}
* public int length() {}
* }
*/
class Solution {
// Function to find the peak of the MountainArray
public int findPeak(MountainArray arr) {
// Step 1: Initialize the search range with low as 0 and high as the last index
int low = 0;
int high = arr.length() - 1;
// Step 2: Perform binary search to find the peak element
while (low < high) {
// Calculate the middle index
int mid = (low + high) / 2;
// Step 3: Check if the middle element is less than or equal to the next element
if (arr.get(mid) <= arr.get(mid + 1)) {
// If true, the peak is on the right side
low = mid + 1;
} else {
// Otherwise, the peak is on the left side
high = mid;
}
}
// Step 4: Return the index of the peak element
return low;
}
// Function to find the target in the MountainArray
public int findInMountainArray(int target, MountainArray arr) {
// Step 1: Find the peak of the MountainArray
int peak = findPeak(arr);
// Step 2: Binary search in the left part of the array (increasing order)
int low = 0, high = peak;
while (low < high) {
// Calculate the middle index
int mid = (low + high) / 2;
// Step 3: Check if the middle element is less than the target
if (arr.get(mid) < target) {
// If true, the target lies on the right side
low = mid + 1;
} else {
// Otherwise, the target lies on the left side
high = mid;
}
}
// Step 4: Check if the target is found in the left part
if (arr.get(low) == target) {
return low;
}
// Step 5: Binary search in the right part of the array (decreasing order)
low = peak;
high = arr.length() - 1;
while (low < high) {
// Calculate the middle index
int mid = (low + high) / 2;
// Step 6: Check if the middle element is greater than the target
if (arr.get(mid) > target) {
// If true, the target lies on the right side
low = mid + 1;
} else {
// Otherwise, the target lies on the left side
high = mid;
}
}
// Step 7: Check if the target is found in the right part
if (arr.get(low) == target) {
return high;
}
// Step 8: If the target is not found, return -1
return -1;
}
}Find in Mountain Array Leetcode Solution in Python
# """
# This is MountainArray's API interface.
# You should not implement it, or speculate about its implementation
# """
#class MountainArray:
# def get(self, index: int) -> int:
# def length(self) -> int:
class Solution:
# Function to find the peak index in the MountainArray
def find_peak(self, mountainArr: 'MountainArray') -> int:
# Step 1: Initialize the search range with low as 0 and high as the last index
low, high = 0, mountainArr.length() - 1
# Step 2: Perform binary search to find the peak element
while low < high:
# Calculate the middle index
mid = (low + high) // 2
# Step 3: Check if the middle element is less than or equal to the next element
if mountainArr.get(mid) <= mountainArr.get(mid + 1):
# If true, the peak is on the right side
low = mid + 1
else:
# Otherwise, the peak is on the left side
high = mid
# Step 4: Return the index of the peak element
return low
# Function to find the target in the MountainArray
def findInMountainArray(self, target: int, mountainArr: 'MountainArray') -> int:
# Step 1: Find the peak index of the MountainArray
peak = self.find_peak(mountainArr)
# Step 2: Binary search in the left part of the array (increasing order)
low, high = 0, peak
while low < high:
# Calculate the middle index
mid = (low + high) // 2
# Step 3: Check if the middle element is less than the target
if mountainArr.get(mid) < target:
# If true, move to the right side
low = mid + 1
else:
# Otherwise, move to the left side
high = mid
# Step 4: Check if the target is found in the left part
if mountainArr.get(low) == target:
return low
# Step 5: Binary search in the right part of the array (decreasing order)
low, high = peak, mountainArr.length() - 1
while low < high:
# Calculate the middle index
mid = (low + high) // 2
# Step 6: Check if the middle element is greater than the target
if mountainArr.get(mid) > target:
# If true, move to the right side
low = mid + 1
else:
# Otherwise, move to the left side
high = mid
# Step 7: Check if the target is found in the right part
if mountainArr.get(low) == target:
return high
# Step 8: If the target is not found, return -1
return -1Find in Mountain Array Leetcode Solution in Javascript
/**
* // This is the MountainArray's API interface.
* // You should not implement it, or speculate about its implementation
* function MountainArray() {
* @param {number} index
* @return {number}
* this.get = function(index) {
* ...
* };
*
* @return {number}
* this.length = function() {
* ...
* };
* };
*/
/**
* @param {number} target
* @param {MountainArray} mountainArr
* @return {number}
*/
var findInMountainArray = function(target, mountainArr) {
// Find peak index of mountain array
const findPeak = () => {
let low = 0;
let high = mountainArr.length() - 1;
while (low < high) {
let mid = Math.floor((low + high) / 2);
if (mountainArr.get(mid) < mountainArr.get(mid + 1)) {
low = mid + 1;
} else {
high = mid;
}
}
return low;
};
// Binary search in ascending order
const binarySearchAsc = (low, high) => {
while (low <= high) {
let mid = Math.floor((low + high) / 2);
let val = mountainArr.get(mid);
if (val === target) return mid;
else if (val < target) low = mid + 1;
else high = mid - 1;
}
return -1;
};
// Binary search in descending order
const binarySearchDesc = (low, high) => {
while (low <= high) {
let mid = Math.floor((low + high) / 2);
let val = mountainArr.get(mid);
if (val === target) return mid;
else if (val > target) low = mid + 1;
else high = mid - 1;
}
return -1;
};
// Step 1: find peak
const peak = findPeak();
// Step 2: search in ascending part
const ascResult = binarySearchAsc(0, peak);
if (ascResult !== -1) return ascResult;
// Step 3: search in descending part
return binarySearchDesc(peak + 1, mountainArr.length() - 1);
};Find in Mountain Array Complexity Analysis
Time Complexity: O(log n)
Time Complexity of Finding the Peak:
The function find_peak() performs a binary search to find the peak of the mountain array. In each iteration, we reduce the search space by half. The number of iterations required to find the peak is logarithmic with respect to the length of the array.
- Time Complexity of find_peak(): O(log n), where n is the number of elements in the array.
Time Complexity of Searching in the Left Side of the Peak:
After finding the peak, we perform binary search in the left half of the array, from index 0 to peak.
- We perform a binary search, which reduces the search space by half in each iteration.
- The time complexity of binary search is O(log n).
Thus, the time complexity of the binary search on the left side is O(log n).
Time Complexity of Searching in the Right Side of the Peak:
Similarly, we perform binary search on the right side of the peak, from index peak to n-1.
- Again, we perform a binary search, reducing the search space by half in each iteration.
- The time complexity of binary search on the right side is also O(log n).
4. Total Time Complexity:
The total time complexity of the algorithm is the sum of the time complexities for the following parts:
- Finding the Peak: O(log n)
- Binary Search on Left Side: O(log n)
- Binary Search on Right Side: O(log n)
Since these steps are performed sequentially, we add their time complexities:
Total Time Complexity = O(log n) + O(log n) + O(log n) = O(log n).
Now let's compute the number of calls and see if they are below 100.
Let's compute the number of calls:
- Finding the peak in log(n): log(104) = 14.
- Searching the first part in log(n): log(104) = 14.
- Searching the second part in log(n): log(104) = 14.
Our total calls to the API if we have an array of size 104 are 14 x 3 = 42 calls which are far less than 100 calls. So, we are sure that our approach is a valid one.
Space Complexity: O(1)
Auxiliary Space Complexity:
Auxiliary space refers to the extra space or temporary space used by an algorithm, excluding the space taken by the input.
In this case:
- The binary search algorithm doesn't require any extra data structures (like arrays or hashmaps).
- We only use a few integer variables:
- low, high, mid for each binary search
- The variable peak to store the peak index
- A few loop control variables.
Thus, the space used for these variables is constant, i.e., O(1).
Total Space Complexity
Total space complexity includes both the space taken by the input and the auxiliary space used by the algorithm.
- The input consists of the MountainArray (which is essentially a list or array of elements). The space taken by this input is O(n), where n is the length of the array.
- The auxiliary space is O(1) as explained above.
Thus, the total space complexity is O(n)
Similar Problems
Now we have successfully tackled this problem, let's try these similar problems:-
You may recall that an array arr is a mountain array if and only if:
- arr.length >= 3
- There exists some index i (0-indexed) with 0 < i < arr.length - 1 such that:
- arr[0] < arr[1] < ... < arr[i - 1] < arr[i]
- arr[i] > arr[i + 1] > ... > arr[arr.length - 1]
Given an integer array nums, return the minimum number of elements to remove to make nums a mountain array.
You and a gang of thieves are planning on robbing a bank. You are given a 0-indexed integer array security, where security[i] is the number of guards on duty on the ith day. The days are numbered starting from 0. You are also given an integer time.
The ith day is a good day to rob the bank if:
- There are at least time days before and after the ith day,
- The number of guards at the bank for the time days before i are non-increasing, and
- The number of guards at the bank for the time days after i are non-decreasing.
More formally, this means day i is a good day to rob the bank if and only if security[i - time] >= security[i - time + 1] >= ... >= security[i] <= ... <= security[i + time - 1] <= security[i + time].
Return a list of all days (0-indexed) that are good days to rob the bank. The order that the days are returned in does not matter.