Find Count of Unique and Duplicate Elements in an Array Solution in C++/Java/Python/JS
In the process of analyzing data within arrays, it's often crucial to differentiate between unique elements and duplicate elements. This can provide insights into the diversity of data, help detect redundancies, or even optimize storage by identifying repeated values. Understanding the frequency of unique versus duplicate elements is a key step in many data analysis tasks. So let’s see how we can identify a unique element and a duplicate in a given array.
Write a program that takes an array whose value lies from 1 to 100 as input and counts the number of unique and duplicate elements.
Examples
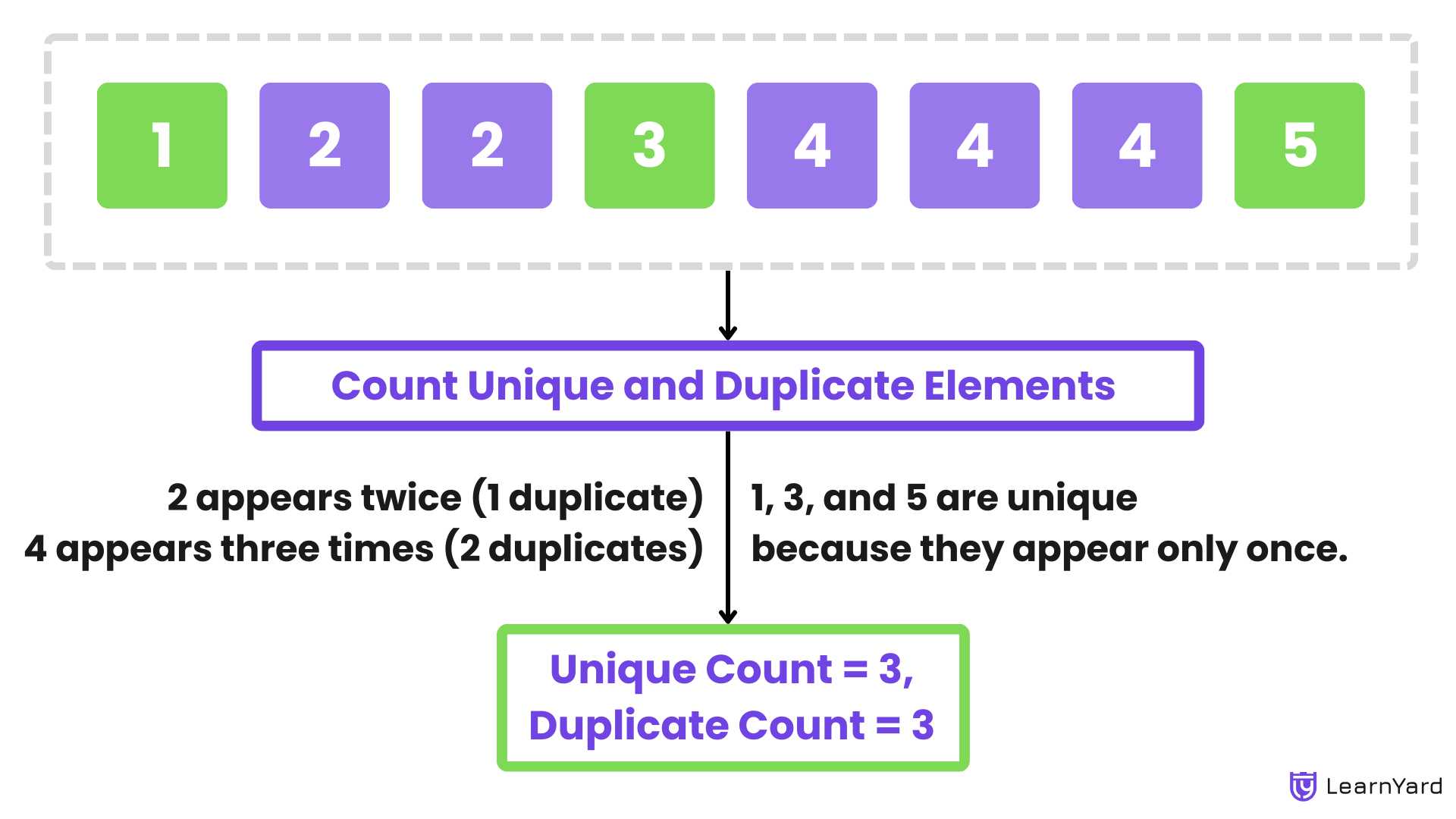
Input: nums = [1, 2, 2, 3, 4, 4, 4, 5]
Output: Unique Count = 3, Duplicate Count = 3
Explanation: In the array [1, 2, 2, 3, 4, 4, 4, 5], the elements 1, 3, and 5 are unique because they appear only once. The elements 2 and 4 are duplicates. Specifically, 2 appears twice (1 duplicate), and 4 appears three times (2 duplicates), giving a total of 3 duplicates.
Input: nums = [7, 7, 7, 7]
Output: Unique Count = 0, Duplicate Count = 3
Explanation: In the array [7, 7, 7, 7], the element 7 appears four times, with 3 duplicates, and no unique elements.
Approach
To determine whether an element is unique or a duplicate, we need to count the frequency of each element in the array. A value is considered unique if it appears exactly once in the array, and it is considered a duplicate if it appears more than once.
In a previous problem, we counted the occurrences of a single target value in an array by using a simple counter. However, this problem requires us to track the frequency of all elements in the array, not just one. Since the values in the array range from 1 to 100, using a separate variable for each possible value would be inefficient and cumbersome.
Instead, we can use a Hash Array
What is a Hash Array?
A hash array is a simple data structure that uses an array to store values based on their hash (or mapped index). In the context of this problem, a hash array is essentially a regular array where the index corresponds to the value in the input array, and the value at that index represents the frequency (or count) of that element.
Example:
Consider an array with elements ranging from 1 to 100. We can create a hash array of size 101 (to cover indices 1 through 100) where:
- The index of the hash array represents the element from the input array.
- The value at that index stores the frequency of that element.
If the element 7 appears three times in the input array, we would increment the value at index 7 in the hash array to 3. This way, the hash array allows us to efficiently track the frequency of every element.
So the first step towards writing the code is to declare and initialize the hash array. A hash array can be declared like a regular array. For this specific problem, since the array elements are expected to be within the range of 1 to 100, the hash array should have 101 elements (index 0 to 100). An initialize the all its values to 0.
Why Do We Take Its Size as 101 Instead of 100?
We take the size of the hash array as 101 rather than 100 as the elements in the input array range from 1 to 100. To directly map each element to an index in the hash array, we need an index that corresponds to each value in this range.If we used a size of 100, the highest index in the array would be 99, which would not allow us to store the frequency of the element 100.
Why is it Initialized with 0?
The purpose of the hash array is to count the occurrences of elements in the input array. Before any elements are processed, the frequency of all elements is zero. Initializing the array with 0 ensures that every index starts with a count of zero. As we traverse the input array, we will increment the corresponding index in the hash array to track how many times each element appears.
After filling the hash_table we will declare two variables unique_count and duplicate_count to count the number of unique and duplicate elements respectively and then, we loop through the array from index 1 to 100:
- If the value at an index is 1 or hash_table[x] == 1, it means the element x is unique, so we increment unique_count.
- If the value is greater than 1 or hash_table[x] > 1, it means the element x has duplicates. We calculate the number of duplicates for that element as frequency - 1 or hash_table[x] -1, and add this to duplicate_count.
Code for All Languages
C++
// Function to count the number of unique and duplicate elements in the array
void countUniqueAndDuplicates(int nums[], int n) {
// Initialize a hash table (array) for values 1 to 100
int hash_table[101] = {0};
// Count frequencies of each element using the hash table
for (int i = 0; i < n; ++i) {
// Increment the frequency count for this number in the hash table
hash_table[nums[i]]++;
}
// Variables to store the counts of unique and duplicate elements
int unique_count = 0, duplicate_count = 0;
// Calculate unique and duplicate counts by traversing the hash table
for (int i = 1; i <= 100; ++i) {
// If the frequency is 1, the element is unique
if (hash_table[i] == 1) {
unique_count++;
}
// If the frequency is greater than 1, the element has duplicates
else if (hash_table[i] > 1) {
// The number of duplicates for this element is (frequency - 1)
duplicate_count += hash_table[i] - 1;
}
}
// Output the results
cout << unique_count << " " << duplicate_count << endl;
}Java
import java.util.Scanner;
public class UniqueAndDuplicateCount {
// Function to count the number of unique and duplicate elements in the array
static void countUniqueAndDuplicates(int[] nums, int n) {
// Initialize a hash table for values 1 to 100
int[] hashTable = new int[101];
// Count frequencies of each element using the hash table
for (int i = 0; i < n; i++) {
// Increment the frequency count for this number in the hash table
hashTable[nums[i]]++;
}
// Variables to store the counts of unique and duplicate elements
int uniqueCount = 0, duplicateCount = 0;
// Calculate unique and duplicate counts by traversing the hash table
for (int i = 1; i <= 100; i++) {
// If the frequency is 1, the element is unique
if (hashTable[i] == 1) {
uniqueCount++;
}
// If the frequency is greater than 1, the element has duplicates
else if (hashTable[i] > 1) {
// The number of duplicates for this element is (frequency - 1)
duplicateCount += hashTable[i] - 1;
}
}
// Output the results
System.out.println(uniqueCount + " " + duplicateCount);
}
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
// Read the size of the array
int n = sc.nextInt();
// Declare and initialize the array
int[] nums = new int[n];
// Read the array elements
for (int i = 0; i < n; i++) {
nums[i] = sc.nextInt();
}
// Call the function to count unique and duplicate elements
countUniqueAndDuplicates(nums, n);
}
}
Python
# Function to count the number of unique and duplicate elements in the array
def count_unique_and_duplicates(nums):
# Initialize a hash table (list) for values 1 to 100
hash_table = [0] * 101
# Count frequencies of each element using the hash table
for num in nums:
# Increment the frequency count for this number in the hash table
hash_table[num] += 1
# Variables to store the counts of unique and duplicate elements
unique_count = 0
duplicate_count = 0
# Calculate unique and duplicate counts by traversing the hash table
for freq in hash_table[1:]: # Only iterate from 1 to 100
# If the frequency is 1, the element is unique
if freq == 1:
unique_count += 1
# If the frequency is greater than 1, the element has duplicates
elif freq > 1:
# The number of duplicates for this element is (frequency - 1)
duplicate_count += freq - 1
# Output the results
print(unique_count, duplicate_count)
Javascript
// Function to count the number of unique and duplicate elements in the array
function countUniqueAndDuplicates(nums) {
// Initialize a hash table (array) for values 1 to 100
const hashTable = Array(101).fill(0);
// Count frequencies of each element using the hash table
for (const num of nums) {
// Increment the frequency count for this number in the hash table
hashTable[num]++;
}
// Variables to store the counts of unique and duplicate elements
let uniqueCount = 0, duplicateCount = 0;
// Calculate unique and duplicate counts by traversing the hash table
for (let i = 1; i <= 100; i++) {
// If the frequency is 1, the element is unique
if (hashTable[i] === 1) {
uniqueCount++;
}
// If the frequency is greater than 1, the element has duplicates
else if (hashTable[i] > 1) {
// The number of duplicates for this element is (frequency - 1)
duplicateCount += hashTable[i] - 1;
}
}
// Output the results
console.log(uniqueCount, duplicateCount);
}Time Complexity : O(n+m)
The time complexity of this problem is O(n + m), where n is the number of elements in the input array, and m is the range of possible values (the size of the frequency table). We first go through the array to build the frequency table, which takes O(n) time. Then, we traverse the frequency table to count unique and duplicate elements, taking O(m) time.
The total time complexity is the sum of both of these complexities which is nothing but
O(n) + O(m) = O(n+m)
Space Complexity : O(m)
Auxiliary Space Complexity: This refers to any extra space used by the algorithm that is independent of the input space and output space. In this case, the extra space is used by the frequency table, which stores counts for m unique elements. Therefore, the auxiliary space complexity is O(m).
Total Space Complexity: This includes the space required for the input, output and extra space used by the algorithm as well. The input array nums[] is of size n, So the space required for input space is O(n). No Output space is used. Space is used by the algorithm that is the space used by the frequency table, which stores counts for m unique elements i.e. O(m).
Total Space Complexity = O(n) + O(1) + O(m) = O(n+m).