Skip to main content

Two Pointer

Find All K-Distant Indices in an Array Solution In C++/Java/Python/JS

Problem Description

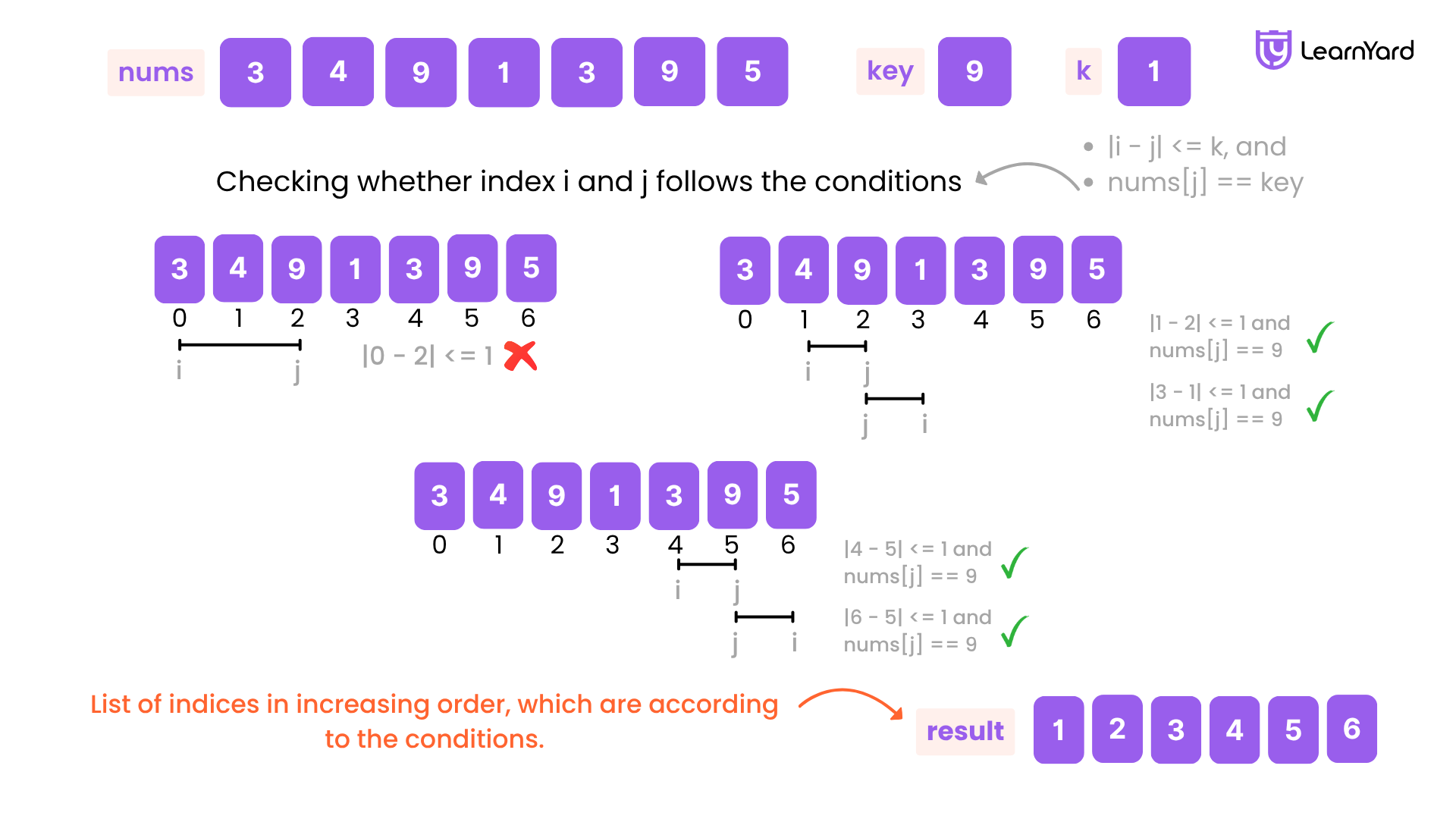
You are given a 0-indexed integer array nums and two integers key and k. An index i in the array is said to be k-distant if there exists at least one index j such that:

  • |i - j| <= k, and
  • nums[j] == key

In simple terms, a k-distant index is one that is at most k positions away from any occurrence of the key in the array. You are required to return a list of all such indices in increasing order.

Example

Input 1:
nums = [3, 4, 9, 1, 3, 9, 5], key = 9, k = 1
Output:
[1, 2, 3, 4, 5, 6]

Explanation:
The key 9 is found at indices 2 and 5.

  • Index 0 is too far from both → not included.
  • Indices 1 to 6 are within distance 1 from either 2 or 5 → included.
    Hence, we return [1, 2, 3, 4, 5, 6].

Input 2:
nums = [2, 2, 2, 2, 2], key = 2, k = 2
Output:
[0, 1, 2, 3, 4]

Explanation:
Every index has the key 2 either at itself or within 2 positions. So all indices are k-distant.

Contraints

  • 1 <= nums.length <= 1000
  • 1 <= nums[i] <= 1000
  • key is guaranteed to be present in nums
  • 1 <= k <= nums.length
At first glance, it seems like for every index i in the array, we might need to scan all nearby indices to check if any of them contains the key and is within a distance k. This immediately hints at a brute force approach with nested loops. However, that can be optimized by flipping the perspective — instead of checking for each index if a nearby key exists, we can first collect all the positions where the key is present, and then from each of those key positions, we mark all indices within distance k as valid. This way, we avoid unnecessary repeated checks and make the logic much cleaner.

Brute Force Approach

Intuition

The most straightforward way to solve this problem is to check every index one by one and look around it — within k distance — to see if any nearby value equals the key. If we find even one match within that window, we mark the current index as valid. Although this method isn’t the most efficient, it’s easy to think about and implement because we’re just simulating the condition as described.

Appraoch

  • Initialize an empty result array to store the k-distant indices.
  • Loop over each index i in the array.
  • For each i, loop over all indices j from i - k to i + k.Make sure j is within array bounds (i.e., between 0 and n - 1).If nums[j] == key, then i is k-distant. Add it to the result and break out of the inner loop.
  • After the outer loop completes, return the result array.

Dry Run

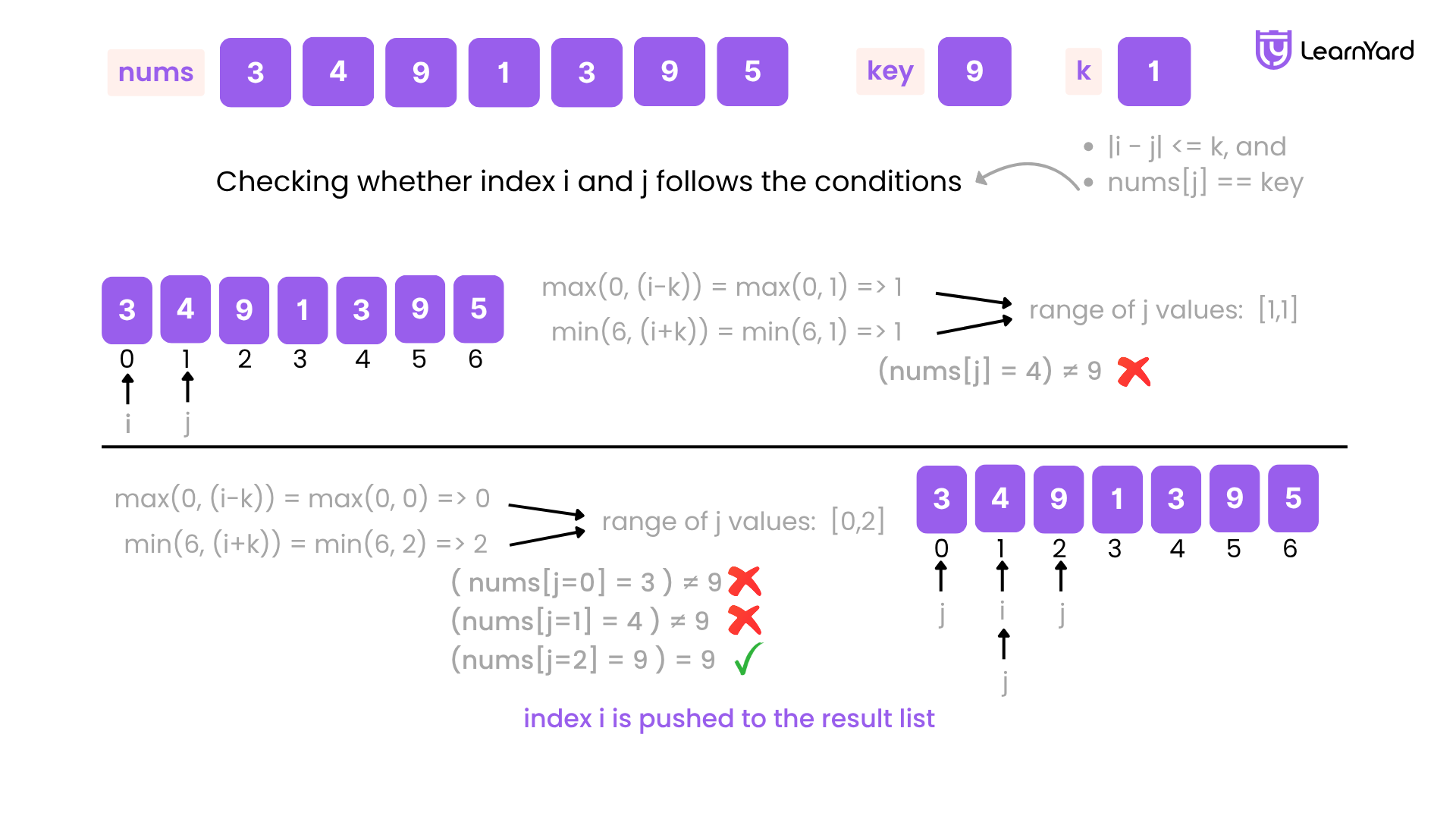
nums = [3, 4, 9, 1, 3, 9, 5], key = 9, k = 1

We’ll go index by index:

  • i = 0: Check j in [max(0, 0-1)=0 to min(6, 0+1)=1] → nums[0]=3, nums[1]=4 → No match → Not added
  • i = 1: Check j = [0,1,2] → nums[2]=9 → Match → Add 1
  • i = 2: nums[2]=9 → Itself is key → Add 2
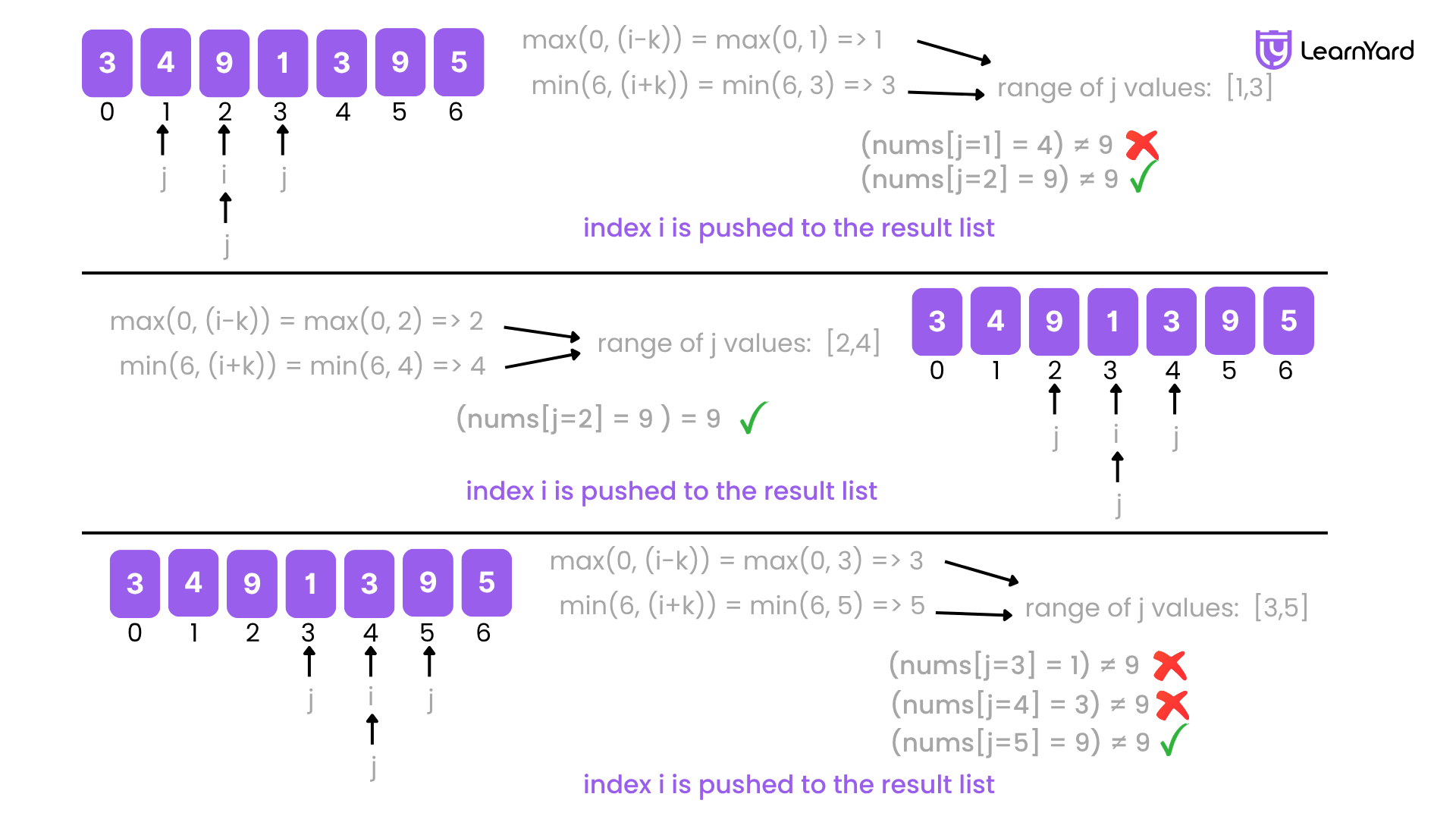
  • i = 3: j = [2,3,4] → nums[2]=9 → Match → Add 3
  • i = 4: j = [3,4,5] → nums[5]=9 → Match → Add 4
  • i = 5: nums[5]=9 → Itself is key → Add 5
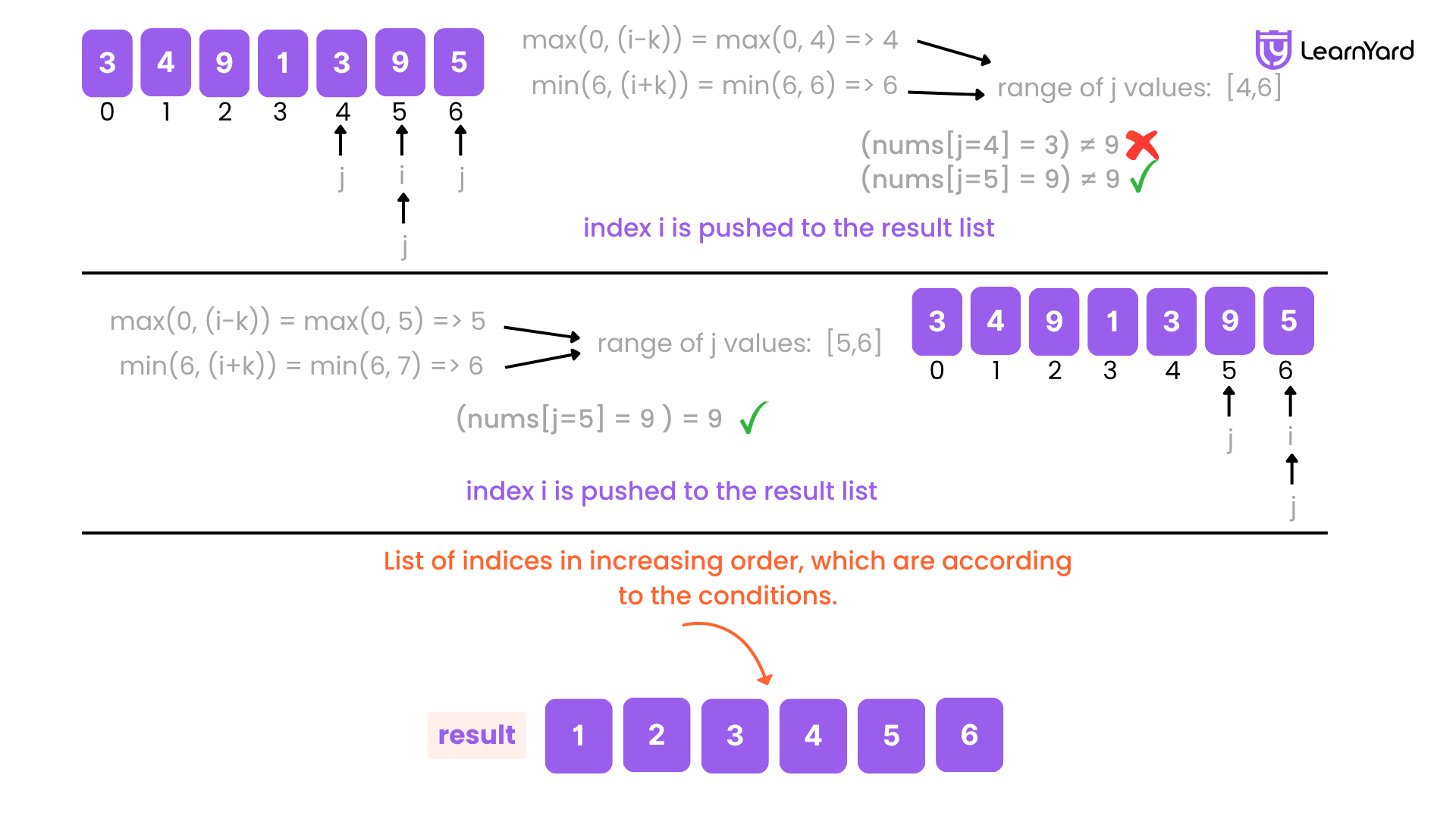
  • i = 6: j = [5,6] → nums[5]=9 → Match → Add 6

Final result:
[1, 2, 3, 4, 5, 6]

Code for All Languages
C++ 
vector<int> find_k_distant_indices(const vector<int>& nums, int key, int k) {
    int n = nums.size();
    vector<int> result;

    for (int i = 0; i < n; i++) {
        for (int j = max(0, i - k); j <= min(n - 1, i + k); j++) {
            if (nums[j] == key) {
                result.push_back(i);
                break;
            }
        }
    }

    return result;
}

Java 
 public static List<Integer> findKDistIndices(int[] nums, int key, int k) {
        int n = nums.length;
        List<Integer> result = new ArrayList<>();

        for (int i = 0; i < n; i++) {
            for (int j = Math.max(0, i - k); j <= Math.min(n - 1, i + k); j++) {
                if (nums[j] == key) {
                    result.add(i);
                    break;
                }
            }
        }

        return result;
    }

Python 
def find_k_distant_indices(nums, key, k):
    n = len(nums)
    result = []

    for i in range(n):
        for j in range(max(0, i - k), min(n, i + k + 1)):
            if nums[j] == key:
                result.append(i)
                break

    return result

Javascript 
function solve(stdin) {
    const lines = stdin.trim().split('\n');
    const nums = lines[0].trim().split(/\s+/).map(Number);
    const [key, k] = lines[1].trim().split(/\s+/).map(Number);
    const n = nums.length;
    const result = [];

    for (let i = 0; i < n; i++) {
        for (let j = Math.max(0, i - k); j <= Math.min(n - 1, i + k); j++) {
            if (nums[j] === key) {
                result.push(i);
                break;
            }
        }
    }

    console.log(result.join(" "));
}

Time Complexity - O(n * k)

  • For each index i from 0 to n - 1, we look at a window of size 2k + 1 (from i - k to i + k).
  • In the worst case, this inner loop runs up to 2k + 1 times per element.
  • So total operations: approximately n * min(n, 2k + 1), which simplifies to O(n × k) (since 2k + 1 is still linear in k).
  • This is acceptable when k is small, but can be slow for large n and k.

Space Complexity - O(n)

  • We are using an extra list/vector result to store the valid indices.
  • In the worst case, every index could be a valid k-distant index (e.g., when all elements are equal to key), so the result array could grow up to size n.
  • Hence, the space complexity is O(n).

Optimized Approach

Intuition

Instead of checking every index i and scanning around it to find a key (which is expensive), we flip the logic. We first find all the positions where key appears in the array. Then, for each such index j, we mark all indices i within k distance from j as valid. This way, we avoid repeated scanning and directly hit the relevant indices.

Approach

  1. Traverse the array once and collect all indices where nums[i] == key.
  2. Use a boolean array or set to mark all indices i where |i - j| <= k for each key index j.
  3. Finally, collect and return all marked indices in sorted order.

This avoids nested iteration for every index and leverages the positions of the key efficiently.

Let us understand this with a vodeo,

0:00
/2:05

Dry Run

Input:
nums = [3, 4, 9, 1, 3, 9, 5], key = 9, k = 1

Step 1: Find key indices → [2, 5]
Step 2: From each key index, mark i in range [j-k, j+k]

  • From 2 → mark [1, 2, 3]
  • From 5 → mark [4, 5, 6]

Marked indices: {1, 2, 3, 4, 5, 6}
Sorted result: [1, 2, 3, 4, 5, 6]

Code for All Languages
C++ 
vector<int> findKDistantIndices(vector<int>& nums, int key, int k) {
    int n = nums.size();
    set<int> indices;

    for (int i = 0; i < n; i++) {
        if (nums[i] == key) {
            int start = max(0, i - k);
            int end = min(n - 1, i + k);
            for (int j = start; j <= end; j++) {
                indices.insert(j);
            }
        }
    }

    return vector<int>(indices.begin(), indices.end());
}

Java 
 public static List<Integer> findKDistantIndices(int[] nums, int key, int k) {
        int n = nums.length;
        TreeSet<Integer> result = new TreeSet<>();

        for (int i = 0; i < n; i++) {
            if (nums[i] == key) {
                int start = Math.max(0, i - k);
                int end = Math.min(n - 1, i + k);
                for (int j = start; j <= end; j++) {
                    result.add(j);
                }
            }
        }

        return new ArrayList<>(result);
    }

Python 
def find_k_distant_indices(nums, key, k):
    n = len(nums)
    marked = set()

    for i in range(n):
        if nums[i] == key:
            for j in range(max(0, i - k), min(n, i + k + 1)):
                marked.add(j)

    return sorted(marked)

Javascript 
function findKDistantIndices(nums, key, k) {
    const n = nums.length;
    const marked = new Set();

    for (let i = 0; i < n; i++) {
        if (nums[i] === key) {
            for (let j = Math.max(0, i - k); j <= Math.min(n - 1, i + k); j++) {
                marked.add(j);
            }
        }
    }

    return Array.from(marked).sort((a, b) => a - b);
}

Time Complexity – O(nk log n)

  • The outer loop runs n times where n is the length of the array. For every index i where nums[i] == key, the inner loop iterates over a window of size up to 2k + 1, marking indices from i - k to i + k. In the worst case, if every element is equal to the key, this results in O(nk) operations.

Additionally, since we're using a TreeSet to store unique indices, each insertion takes O(log n) time. Therefore, the overall time complexity becomes:

O(nk log n)

Space Complexity - O(n)

We're using a TreeSet to store unique indices, which at most can hold n elements. After processing, we convert it to a list. Both structures together use extra space proportional to the number of stored indices.

Thus, the space complexity is:O(n)


Similar Questions

Two Sum

Given an array of integers nums and an integer target, return indices of the two numbers such that they add up to target.

Minimum Absolute Difference Between Elements With Constraint

You're given a 0-indexed array nums and an integer x.
Your task is to find the minimum absolute difference between any two elements in nums such that the indices are at least x apart.
Return the smallest abs(nums[i] - nums[j]) where |i - j| >= x.