Decimal to Binary Solution In C++/Java/Python/JS
Problem Description
Given a decimal number n, return its binary equivalent.
What is Binary Representation of a Number?
Binary representation of a number is a way of expressing it using only two digits: 0 and 1. Each digit represents a power of 2, starting from the right (least significant bit). Just like we use powers of 10 in the decimal system, binary uses powers of 2. Computers store and process all numbers in this binary format.
Note: For Detailed Explanation and Visualization, Read full Article.
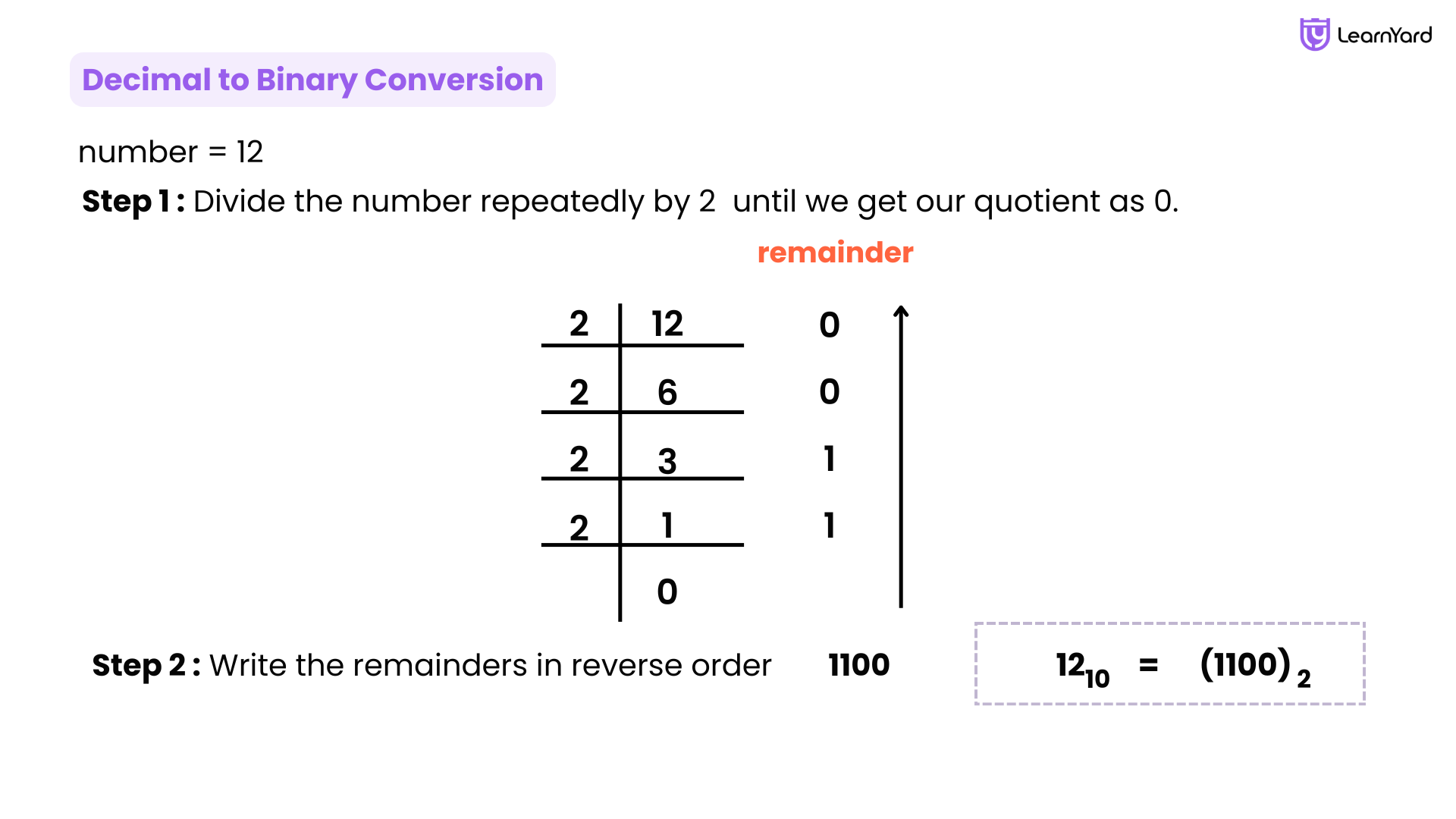
Example
Input: n = 12
Output: 1100
Explanation: The binary representation of 12 is "1100". To convert 12 to binary:
- 12 ÷ 2 = 6, remainder = 0
- 6 ÷ 2 = 3, remainder = 0
- 3 ÷ 2 = 1, remainder = 1
- 1 ÷ 2 = 0, remainder = 1
Now, reading the remainders in reverse order: 1 1 0 0 → 1100
Input: n = 33
Output: 100001
Explanation: The binary representation of 33 is "100001". To convert 33 to binary:
- 33 ÷ 2 = 16, remainder = 1
- 16 ÷ 2 = 8, remainder = 0
- 8 ÷ 2 = 4, remainder = 0
- 4 ÷ 2 = 2, remainder = 0
- 2 ÷ 2 = 1, remainder = 0
- 1 ÷ 2 = 0, remainder = 1
Reading the remainders in reverse order: 1 0 0 0 0 1 → 100001
Constraints
- 1 <= n <= 231 - 1
One of the foundational steps in bit manipulation is understanding how to convert a decimal number into its binary representation. Let's explore how to do it in simplest way
Optimal Approach
Intuition
The decimal system is the one we use every day. It’s a base-10 system, which means it uses 10 different digits: from 0 to 9. Each digit’s position represents a power of 10. For example, the number 345 in decimal means:
- 3 × 10² (which is 3 × 100 = 300)
- 4 × 10¹ (which is 4 × 10 = 40)
- 5 × 10⁰ (which is 5 × 1 = 5)
Adding these together gives us 345.
Now, the binary system works a bit differently. It is a base-2 system, meaning it uses only two digits: 0 and 1. These two digits represent powers of 2 instead of 10. So each position in a binary number tells us how many times we multiply by 2 raised to a certain power.
For example, the binary number 1011 represents:
- 1 × 2³ (which is 1 × 8 = 8)
- 0 × 2² (which is 0 × 4 = 0)
- 1 × 2¹ (which is 1 × 2 = 2)
- 1 × 2⁰ (which is 1 × 1 = 1)
Adding these together gives us 8 + 0 + 2 + 1 = 11 in decimal.
So, while decimal has 10 possible digits (0 through 9) to express numbers, binary only has 2 possible digits (0 and 1). This is why when converting decimal numbers to binary, we repeatedly divide by 2 — because the binary system counts in powers of 2, and the remainder after division tells us which digit (0 or 1) to place in each position.
When we want to convert a decimal number into its binary form, the key idea is to repeatedly divide the number by 2 and keep track of the remainders. The remainder when dividing by 2 tells us whether the current bit is 0 or 1 — if the remainder is 0, that bit is 0; if it’s 1, that bit is 1. Since division naturally reduces the number step by step, we move from the least significant bit (rightmost) to the most significant bit (leftmost) by continuously dividing the number n by 2 until it becomes zero.
What is Least and Most Significant Bit in Binary?
Every binary number is made up of bits arranged from left to right. The Most Significant Bit (MSB) is the bit at the extreme left — it holds the highest place value, meaning it contributes the most to the overall value of the number. On the other hand, the Least Significant Bit (LSB) is the bit at the extreme right — it has the smallest place value and represents the units place (2⁰).
For example, consider the binary number 1011.
- The MSB is the leftmost bit, which is 1 here.
- The LSB is the rightmost bit, which is also 1 here.
One important thing to understand is the order in which we get these bits. Because division by 2 gives the remainder starting from the least significant bit, we get the binary digits in reverse order of how we want to read them. For example, if we convert 12 to binary, the remainders come out as 0, 0, 1, 1 in that order. But the actual binary representation should be 1100, so we need to insert each new bit at the front of our result string binary. This way, the final string builds up in the correct order from the most significant bit to the least significant bit.
A common question that arises is: what if the number is 0? We can’t just run the division steps because that would never start properly. So, we handle this as a special case by returning "0" immediately if the input is zero.
Once all divisions are done and the number becomes zero, the string we have built represents the exact binary equivalent of the decimal number n. This process is simple, efficient, and forms the basis of many bit manipulation techniques we use later on.
Approach
Step 1: Handle the Edge Case
Before entering the loop, we check if the input number n is equal to 0.
If it is, then the binary representation is simply "0", so we return it directly.
This prevents unnecessary calculations for the zero case.
Step 2: Initialize the Result String
We declare an empty string named binary.
This string will be used to store the binary digits as we compute them.
Each digit will be inserted at the front to ensure correct order.
Step 3: Loop Until the Number Becomes 0
We use a while loop that runs while n > 0.
In each iteration, we perform two key operations:
- Compute the remainder of n divided by 2 (which gives the current binary digit)
- Divide n by 2 (to move on to the next bit in the next iteration)
Step 4: Convert Remainder to Character and Append
We convert the remainder (either 0 or 1) into a character by adding it to '0'.
This character is then prepended to the binary string using string concatenation.
This is done because binary digits are obtained from least significant to most significant, and we want them in the correct order.
Step 5: Continue Until All Digits Are Processed
We repeat the division and remainder process until n becomes 0.
At this point, all binary digits have been computed and stored in the string binary.
Step 6: Return the Final Result
After the loop ends, we return the complete binary string binary.
This string represents the binary form of the input decimal number.

Dry Run
Let's do a detailed Dry Run of the decimal to binary conversion approach for the input:
n = 33
We want to convert the decimal number 33 to its binary representation.
Step 1: Initialize Variables
We start with:
n = 33
binary = "" (an empty string to store the binary digits)
Step 2: Loop Until n Becomes 0
We use a while loop that continues as long as n > 0.
In each iteration, we:
- Compute remainder = n % 2
- Convert the remainder to a character (either '0' or '1')
- Prepend it to the binary string
- Divide n by 2 using integer division
Iteration-Wise Dry Run
Iteration 1
n = 33
remainder = 33 % 2 = 1
binary = '1' + "" = "1"
n = 33 / 2 = 16
Iteration 2
n = 16
remainder = 16 % 2 = 0
binary = '0' + "1" = "01"
n = 16 / 2 = 8
Iteration 3
n = 8
remainder = 8 % 2 = 0
binary = '0' + "01" = "001"
n = 8 / 2 = 4
Iteration 4
n = 4
remainder = 4 % 2 = 0
binary = '0' + "001" = "0001"
n = 4 / 2 = 2
Iteration 5
n = 2
remainder = 2 % 2 = 0
binary = '0' + "0001" = "00001"
n = 2 / 2 = 1
Iteration 6
n = 1
remainder = 1 % 2 = 1
binary = '1' + "00001" = "100001"
n = 1 / 2 = 0
Loop ends as n is now 0.
Final Result
The binary representation of 33 is "100001".
Code for All Languages
C++
#include <iostream> // for cin and cout
#include <string> // for using string and storing binary
using namespace std;
class Solution {
public:
// Function to convert a decimal number to its binary representation
string decToBinary(int n) {
// Step 1: Edge case for 0
if (n == 0) return "0";
string binary = ""; // To store the binary digits in reverse order
// Step 2: Keep dividing the number by 2 and storing the remainder
while (n > 0) {
int remainder = n % 2;
binary = char(remainder + '0') + binary; // Append at front
n = n / 2;
}
// Step 3: Return the final binary string
return binary;
}
};
// Driver code
int main() {
int n;
// Input the decimal number
cin >> n;
Solution sol;
string binaryString = sol.decToBinary(n);
// Output the binary representation
cout << binaryString << endl;
return 0;
}
Java
import java.util.Scanner; // for taking input
class Solution {
// Function to convert a decimal number to its binary representation
String decToBinary(int n) {
// Step 1: Edge case for 0
if (n == 0) return "0";
String binary = ""; // To store the binary digits in reverse order
// Step 2: Keep dividing the number by 2 and storing the remainder
while (n > 0) {
int remainder = n % 2;
binary = (char)(remainder + '0') + binary; // Append at front
n = n / 2;
}
// Step 3: Return the final binary string
return binary;
}
}
// Driver code
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n;
// Input the decimal number
n = sc.nextInt();
Solution sol = new Solution();
String binaryString = sol.decToBinary(n);
// Output the binary representation
System.out.println(binaryString);
sc.close();
}
}Python
class Solution:
# Function to convert a decimal number to its binary representation
def decToBinary(self, n):
# Step 1: Edge case for 0
if n == 0:
return "0"
binary = "" # To store the binary digits in reverse order
# Step 2: Keep dividing the number by 2 and storing the remainder
while n > 0:
remainder = n % 2
binary = chr(remainder + ord('0')) + binary # Append at front
n = n // 2
# Step 3: Return the final binary string
return binary
# Driver code
if __name__ == "__main__":
n = int(input()) # Input the decimal number
sol = Solution()
binaryString = sol.decToBinary(n)
# Output the binary representation
print(binaryString)Javascript
/**
* @param {number} n
* @return {string}
*/
class Solution {
// Function to convert a decimal number to its binary representation
decToBinary(n) {
// Step 1: Edge case for 0
if (n === 0) return "0";
let binary = ""; // To store the binary digits in reverse order
// Step 2: Keep dividing the number by 2 and storing the remainder
while (n > 0) {
let remainder = n % 2;
binary = String.fromCharCode(remainder + '0'.charCodeAt(0)) + binary; // Append at front
n = Math.floor(n / 2);
}
// Step 3: Return the final binary string
return binary;
}
}
// Driver code
const readline = require('readline');
const rl = readline.createInterface({
input: process.stdin,
output: process.stdout
});
// Input the decimal number
rl.question('', function(input) {
const n = parseInt(input);
const sol = new Solution();
const binaryString = sol.decToBinary(n);
// Output the binary representation
console.log(binaryString);
rl.close();
});Time Complexity: O((log n)²)
Number of Iterations: O(log n)
The while loop runs as long as n > 0 and divides n by 2 in each iteration.
This means the number of iterations depends on how many times we can divide n by 2 until it becomes 0.
Hence, the number of iterations is approximately log₂(n), which gives us O(log n) time.
Remainder Calculation and Character Conversion: O(1)
In each iteration:
- We calculate remainder = n % 2 → constant time O(1)
- We convert it to a character using char(remainder + '0') → also O(1)
String Concatenation (Front Insertion): O(m)
Here, m = number of bits in the binary representation ≈ log₂(n)
Since strings are immutable in C++, adding a character to the front of a string takes O(length of string so far) time.
Therefore, the total cost of inserting characters at the front is:
- 1st bit → O(1)
- 2nd bit → O(2)
- 3rd bit → O(3)
- ...
- log n-th bit → O(log n)
This results in a series: 1 + 2 + 3 + ... + log n = O((log n)²)
Final Time Complexity: O((log n)²)
- The loop runs O(log n) times
- Each front insertion takes up to O(log n) time
- Therefore, total time = O(log n × log n) = O((log n)²)
Where:
- n = the given decimal number
- log n = number of bits needed to represent n in binary
Space Complexity: O(1)
Auxiliary Space Complexity: O(1)
This refers to the extra space used by the algorithm that is independent of the input and output storage.
In this decimal-to-binary conversion approach, we use:
- An integer variable remainder to store the result of modulo operation in each iteration
- A string variable binary to build the binary result
- The input number n, which is modified during the computation
All these are basic primitive types, and their usage does not depend on the value of n.
No additional data structures like arrays, lists, or maps are used during computation.
Therefore, the auxiliary space used is constant, i.e., O(1).
Total Space Complexity: O(log n)
This includes:
- Output space: The binary representation of an integer n will have at most log₂(n) + 1 bits
So the string binary that stores the result will require O(log n) space - Auxiliary space: As analyzed above, this is O(1)
Combining all the components:
Total Space Complexity = O(log n) + O(1) = O(log n)
Similar Problems
Given an integer n, return an array ans of length n + 1 such that for each i (0 <= i <= n), ans[i] is the number of 1's in the binary representation of i.
Given a positive integer n, write a function that returns the number of set bits in its binary representation.