Daily Temperatures Solution In C++/Java/Python/JS
Problem Description
Given an array of integers temperatures represents the daily temperatures, return an array answer such that answer[i] is the number of days you have to wait after the ith day to get a warmer temperature. If there is no future day for which this is possible, keep answer[i] == 0 instead.
Examples
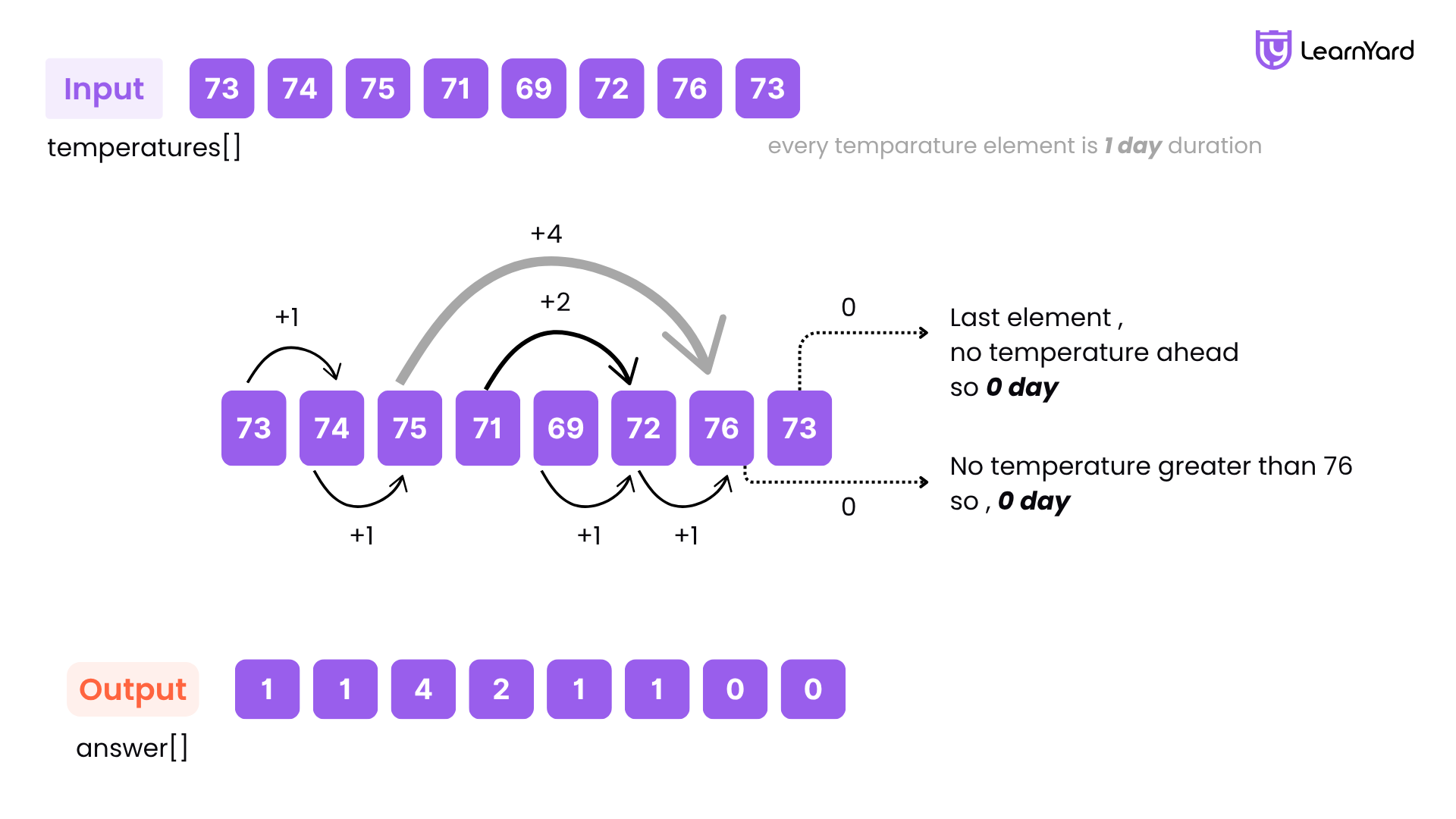
Input: temperatures = [73, 74, 75, 71, 69, 72, 76, 73]
Output: [1, 1, 4, 2, 1, 1, 0, 0]
Explanation:
For each day, we look for the next day with a warmer temperature:
- Day 0 (73): next warmer day is Day 1 (74) → wait 1 day.
- Day 1 (74): next warmer day is Day 2 (75) → wait 1 day.
- Day 2 (75): next warmer day is Day 6 (76) → wait 4 days.
- Day 3 (71): next warmer day is Day 5 (72) → wait 2 days.
- Day 4 (69): next warmer day is Day 5 (72) → wait 1 day.
- Day 5 (72): next warmer day is Day 6 (76) → wait 1 day.
- Day 6 (76): no warmer day → 0.
- Day 7 (73): no warmer day → 0.
Input: temperatures = [30, 40, 50, 60]
Output: [1, 1, 1, 0]
Explanation:
- Day 0 (30): next warmer day is Day 1 (40) → wait 1 day.
- Day 1 (40): next warmer day is Day 2 (50) → wait 1 day.
- Day 2 (50): next warmer day is Day 3 (60) → wait 1 day.
- Day 3 (60): no warmer day → 0.
Input: temperatures = [30, 60, 90]
Output: [1, 1, 0]
Explanation:
- Day 0 (30): next warmer day is Day 1 (60) → wait 1 day.
- Day 1 (60): next warmer day is Day 2 (90) → wait 1 day.
- Day 2 (90): no warmer day → 0.
Constraints
1 <= temperatures.length <= 105
30 <= temperatures[i] <= 100
The first question that comes to mind after reading the problem is: How do we find, for each day, the next day with a warmer temperature?
A straightforward idea is to simply check each day against all future days until we find a warmer one.
To build a clear understanding, let’s first explore this brute-force approach before moving on to more optimized solutions.
Brute-Force Approach
Intuition
Since we want to find out, for each day, how many days we have to wait until we see a warmer temperature, the first idea that comes to our mind is to look ahead from each day and check all future temperatures one by one.
For example, if today is day i, then we check temperatures on days:
i + 1, i + 2, ..., until we find a day j where:
temperature[j] > temperature[i].
Why Exactly Check All Future Days?
The problem explicitly asks: how many days must we wait to get a warmer temperature?
To answer this accurately for every day, we must know exactly when the next warmer temperature appears in the future. Since the temperatures may fluctuate, the only straightforward way is to check each future day individually and see if it is warmer than the current day.
For this, we can use a nested loop:
- The outer loop fixes the current day i.
- The inner loop looks forward from i + 1 up to the last day, searching for the first warmer temperature.
Checking Future Days using Nested Loops
We first fix the index i in temperatures using an outer loop.
This loop runs from i = 0 to i = n - 1, where n is the length of the temperatures array.
For each fixed day i, we use an inner loop with index j starting from i + 1 and running up to n - 1.
At each step, we compare temperatures[j] with temperatures[i]:
If temperatures[j] > temperatures[i], it means we found a warmer day.
The number of days waited is then j - i.
We can break out of the inner loop since we only need the first warmer day.
If no such warmer day is found after i, we leave answer[i] as 0 (meaning there is never a warmer temperature in the future).
Approach
Step 1: Initialize the answer array
Create an array answer of the same length as the input temperatures array.
Set all elements initially to 0.
This array will store, for each day, the number of days we have to wait to get a warmer temperature.
Step 2: Loop to fix the current day whose warmer temperature we want to find
Use an outer loop where index i ranges from 0 to n - 1 (where n is the number of days / length of temperatures).
This picks each day one by one as the day we are checking from.
Step 3: Loop to check all future days after day i
For each day i, use another loop where index j starts from i + 1 and runs up to n - 1.
This loop checks all future days after i to find the next day with a warmer temperature.
Step 4: Compare temperatures on day j and day i
Inside the inner loop, check: if temperatures[j] > temperatures[i], it means we have found a warmer day in the future.
Step 5: Update the answer for day i
If we found such a day j, compute the number of days waited: j - i.
Set answer[i] = j - i.
Step 6: Break out of inner loop after finding the first warmer day
Since we only care about the first warmer day, we immediately break out of the inner loop after updating answer[i].
Step 7: Return the answer array
After both loops complete, return the answer array.
Dry Run
Let’s do a detailed dry run of the brute-force approach using nested loops
for the input:
temperatures = [73,74,75,71,69,72,76,73]
We want to build the answer array where for each day, we find how many days we have to wait to get a warmer temperature.
Step 1: Initialize answer array
Create answer = [0,0,0,0,0,0,0,0]
Length of temperatures, n = 8
Step 2: Loop over each day as the current day i
We’ll use an outer loop with index i from 0 to 7, and for each day, check all future days with an inner loop.
Iteration-wise Dry Run
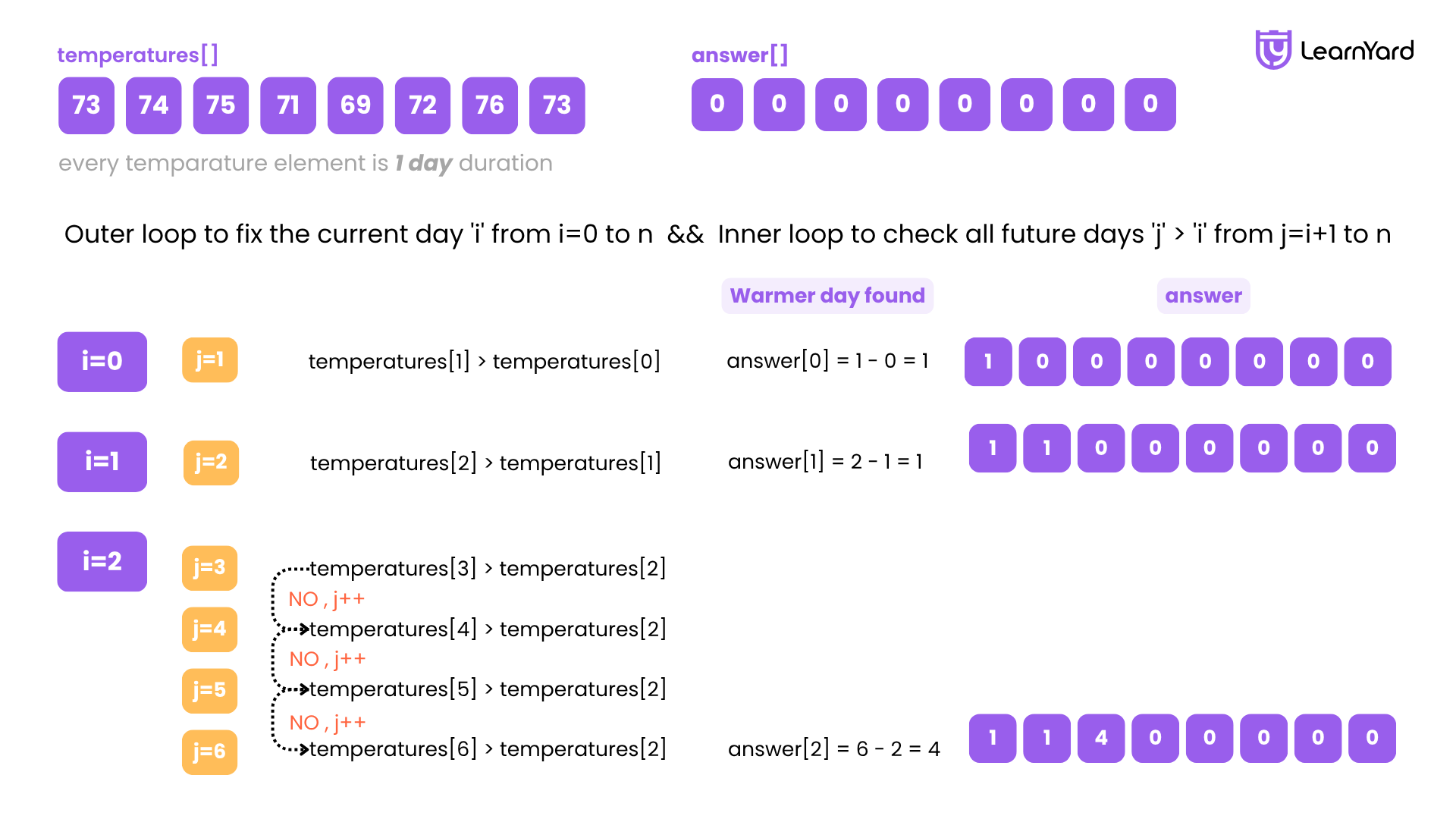
i = 0 (temperature = 73)
Check future days (j > i):
j=1: temperature=74 > 73 → found warmer
answer[0]=1 (days waited: 1)
Break inner loop
Current answer: [1,0,0,0,0,0,0,0]
i = 1 (temperature = 74)
j=2: temperature=75 > 74 → found warmer
answer[1]=2-1=1
Break inner loop
Current answer: [1,1,0,0,0,0,0,0]
i = 2 (temperature = 75)
j=3: temperature=71 → not warmer
j=4: temperature=69 → not warmer
j=5: temperature=72 → not warmer
j=6: temperature=76 > 75 → found warmer
answer[2]=6-2=4
Break
Current answer: [1,1,4,0,0,0,0,0]
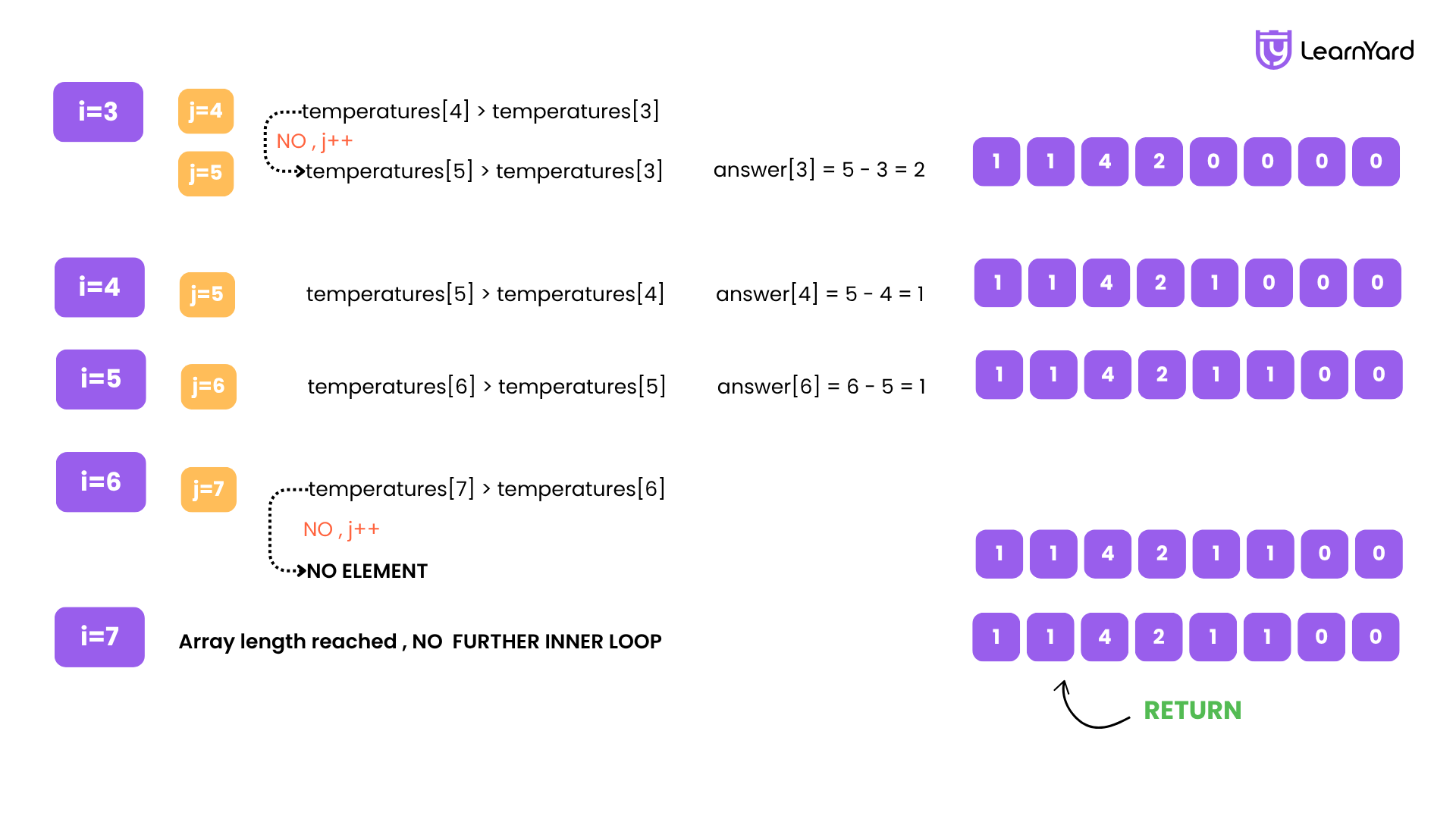
i = 3 (temperature = 71)
j=4: temperature=69 → not warmer
j=5: temperature=72 > 71 → found warmer
answer[3]=5-3=2
Break
Current answer: [1,1,4,2,0,0,0,0]
i = 4 (temperature = 69)
j=5: temperature=72 > 69 → found warmer
answer[4]=5-4=1
Break
Current answer: [1,1,4,2,1,0,0,0]
i = 5 (temperature = 72)
j=6: temperature=76 > 72 → found warmer
answer[5]=6-5=1
Break
Current answer: [1,1,4,2,1,1,0,0]
i = 6 (temperature = 76)
j=7: temperature=73 → not warmer
No warmer found → keep answer[6]=0
i = 7 (temperature = 73)
No future day → answer[7]=0
Final Result
answer = [1,1,4,2,1,1,0,0]
Meaning:
Day 0: wait 1 day to get warmer temperature
Day 1: wait 1 day
Day 2: wait 4 days
Day 3: wait 2 days
Day 4: wait 1 day
Day 5: wait 1 day
Day 6 & 7: no warmer temperature in future → 0
Code for All Languages
C++
#include <iostream> // For input and output functions like cin and cout
#include <vector> // For using the vector data structure
using namespace std;
class Solution {
public:
vector<int> dailyTemperatures(vector<int>& temperatures) {
int n = temperatures.size(); // Number of days
// Step 1: Initialize the answer array
vector<int> answer(n, 0); // Initially fill with zeros
// Step 2: Outer loop to fix the current day 'i'
for (int i = 0; i < n; i++) {
// Step 3: Inner loop to check all future days 'j' > 'i'
for (int j = i + 1; j < n; j++) {
// Step 4: Check if temperature at day 'j' is warmer than at day 'i'
if (temperatures[j] > temperatures[i]) {
// Step 5: Update answer[i] with the number of days waited
answer[i] = j - i;
// Step 6: Break after finding the first warmer day
break;
}
}
}
// Step 7: Return the answer array as the required value
return answer;
}
};
int main() {
int n;
cin >> n; // Input number of days
vector<int> temperatures(n);
// Input the temperatures
for (int i = 0; i < n; i++) {
cin >> temperatures[i];
}
Solution sol;
vector<int> result = sol.dailyTemperatures(temperatures);
// Output the result
for (int days : result) {
cout << days << " ";
}
return 0;
}
Java
import java.util.*; // For Scanner and Arrays
class Solution {
public int[] dailyTemperatures(int[] temperatures) {
int n = temperatures.length; // Number of days
// Step 1: Initialize the answer array
int[] answer = new int[n]; // By default, filled with zeros
// Step 2: Outer loop to fix the current day 'i'
for (int i = 0; i < n; i++) {
// Step 3: Inner loop to check all future days 'j' > 'i'
for (int j = i + 1; j < n; j++) {
// Step 4: Check if temperature at day 'j' is warmer than at day 'i'
if (temperatures[j] > temperatures[i]) {
// Step 5: Update answer[i] with the number of days waited
answer[i] = j - i;
// Step 6: Break after finding the first warmer day
break;
}
}
}
// Step 7: Return the answer array as the required value
return answer;
}
}
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
// Input number of days
int n = sc.nextInt();
int[] temperatures = new int[n];
// Input the temperatures
for (int i = 0; i < n; i++) {
temperatures[i] = sc.nextInt();
}
Solution sol = new Solution();
int[] result = sol.dailyTemperatures(temperatures);
// Output the result
for (int days : result) {
System.out.print(days + " ");
}
}
}Python
from typing import List # For specifying type hints
class Solution:
def dailyTemperatures(self, temperatures: List[int]) -> List[int]:
n = len(temperatures) # Number of days
# Step 1: Initialize the answer list
answer = [0] * n # By default, filled with zeros
# Step 2: Outer loop to fix the current day 'i'
for i in range(n):
# Step 3: Inner loop to check all future days 'j' > 'i'
for j in range(i + 1, n):
# Step 4: Check if temperature at day 'j' is warmer than at day 'i'
if temperatures[j] > temperatures[i]:
# Step 5: Update answer[i] with the number of days waited
answer[i] = j - i
# Step 6: Break after finding the first warmer day
break
# Step 7: Return the answer list as the required value
return answer
if __name__ == "__main__":
# Input number of days
n = int(input())
# Input the temperatures
temperatures = list(map(int, input().split()))
sol = Solution()
result = sol.dailyTemperatures(temperatures)
# Output the result
print(' '.join(map(str, result)))
Javascript
/**
* @param {number[]} temperatures
* @return {number[]}
*/
var dailyTemperatures = function(temperatures) {
const n = temperatures.length; // Number of days
// Step 1: Initialize the answer array
const answer = Array(n).fill(0); // Default is 0 for each day
// Step 2: Outer loop to fix the current day 'i'
for (let i = 0; i < n; i++) {
// Step 3: Inner loop to check all future days 'j' > 'i'
for (let j = i + 1; j < n; j++) {
// Step 4: Check if temperature at day 'j' is warmer than at day 'i'
if (temperatures[j] > temperatures[i]) {
// Step 5: Update answer[i] with the number of days waited
answer[i] = j - i;
// Step 6: Break after finding the first warmer day
break;
}
}
}
// Step 7: Return the answer array as the required value
return answer;
};
// Driver code
const readline = require("readline");
const rl = readline.createInterface({
input: process.stdin,
output: process.stdout
});
let inputs = [];
let n;
rl.on("line", function(line) {
inputs.push(line.trim());
if (inputs.length === 2) {
// First line: number of days
n = parseInt(inputs[0]);
// Second line: list of temperatures
const temperatures = inputs[1].split(' ').map(Number);
const result = dailyTemperatures(temperatures);
console.log(result.join(' '));
rl.close();
}
});
Time Complexity: O(n²)
Let’s denote: n = length of the array temperatures.
Outer Loop: O(n)
The outer loop fixes the current day i and runs from i = 0 to i = n - 1.
So, it executes exactly n times.
Inner Loop: O(n)
For each fixed day i, the inner loop checks all future days from j = i + 1 to j = n - 1.
In the worst case, when the temperatures are in decreasing order, the inner loop can run up to (n - i - 1) times.
Total Time per Outer Loop Iteration: O(n)
For each i, the inner loop may do up to O(n) work in the worst case.
Final Time Complexity: O(n²)
Adding it all together:
– The outer loop runs n times.
– Each time, we may do up to O(n) comparisons in the inner loop.
So the total complexity becomes: O(n) × O(n) = O(n²).
Space Complexity: O(n)
Auxiliary Space Complexity: O(n)
This refers to the extra space used by the algorithm beyond the input itself.
In our brute-force approach, we create an answer array of length n, where n is the number of days in the input.
This array stores, for each day, the number of days until a warmer temperature.
Other than the answer array, we only use a few integer variables like loop counters and temporary variables, which take O(1) space.
Hence, the auxiliary space complexity is O(n).
Total Space Complexity: O(n)
This includes:
– Input space: The input array temperatures of length n → O(n).
– Output space: The answer array of length n → O(n).
– Extra space used by the algorithm (auxiliary): as analyzed above, O(n).
Total Space Complexity = O(n).
Will brute force work against the given constraints?
For the current solution, the time complexity is O(n²), which is not suitable for n ≤ 10⁵. This means that for each test case, where the length of the array is at most 10⁵, the solution might not execute within the given time limits.
Since O(n²) results in a maximum of 10¹⁰ operations (for n = 10⁵), the solution is not expected to work well for larger test cases. In most competitive programming environments, problems can handle up to 10⁶ operations per test case, meaning that for n ≤ 10⁵, the solution with 10¹⁰ operations is not efficient enough.
When multiple test cases are involved, the total number of operations could easily exceed this limit and approach 10¹⁰ operations, especially when there are many test cases or the value of n increases.
Thus, while the solution meets the time limits for a single test case, the O(n²) time complexity poses a risk for Time Limit Exceeded (TLE) errors when handling larger input sizes or multiple test cases. This can be a challenge for competitive programming problems with larger inputs or numerous test cases.
We’ve seen the brute-force solution, which checks every future day and runs in O(n²) time. While it builds intuition, it’s too slow for large inputs. Can we avoid redundant checks and find a smarter, faster way? Let’s explore the optimal approach next.
Optimal Approach
Intuition
To improve the time complexity of finding the number of days until a warmer temperature, we need to identify patterns in the problem that can guide us towards a more efficient solution. Let’s analyze the input temperatures array from left to right and consider the following observations:
Important Observations
When traversing the temperatures array, we can encounter two main cases:
Decreasing Order Sequence:
In a sequence where temperatures keep decreasing, all previous days are waiting for a warmer day in the future.
For example, in the sequence [75, 74, 71], the next warmer temperature (say 76) becomes the answer for all of them:
– The next warmer temperature for 71 is 76 (waited 3 days).
– For 74, it’s also 76 (waited 2 days).
– For 75, it’s also 76 (waited 1 day).
Increasing Order Sequence:
In an increasing sequence like [70, 72, 74], each day’s next warmer day is simply the very next day:
– For 70, the next warmer temperature is 72.
– For 72, the next warmer temperature is 74.
To identify the next warmer days efficiently
We can traverse the array from left to right.
When we find a temperature higher than previous waiting days, that temperature becomes the next warmer temperature for those waiting days:
– We then record how many days they had to wait (difference of indices).
– This process repeats every time we encounter a new warmer temperature.
– Each day only waits until a warmer temperature appears, and we never have to recheck it later.
Where to store Previous Waiting Days?
As we traverse the temperatures array and encounter days that need to wait for their next warmer day, we need an efficient way to remember which days are still waiting.
Let’s use an array treated as a stack to simulate this process step by step.
Initial Setup
temperatures = [73,74,75,71,69,72,76,73]
Stored Indices (Stack): []
Answer Array: [0,0,0,0,0,0,0,0]
Step 1: Current Element → temperatures[0] = 73
No previous elements to compare.
Store index 0 in stack.
Stored Indices: [0]
Answer Array: [0,0,0,0,0,0,0,0]
Step 2: Current Element → temperatures[1] = 74
74 > 73 (temperature at index 0) → next warmer day for index 0 is index 1.
Update answer[0] = 1 - 0 = 1.
Remove 0 from stack.
Store index 1.
Stored Indices: [1]
Answer Array: [1,0,0,0,0,0,0,0]
Step 3: Current Element → temperatures[2] = 75
75 > 74 (temperature at index 1) → next warmer day for index 1 is index 2.
Update answer[1] = 2 - 1 = 1.
Remove 1 from stack.
Store index 2.
Stored Indices: [2]
Answer Array: [1,1,0,0,0,0,0,0]
Step 4: Current Element → temperatures[3] = 71
71 < 75 → just store index 3.
Stored Indices: [2,3]
Answer Array: [1,1,0,0,0,0,0,0]
Step 5: Current Element → temperatures[4] = 69
69 < 71 → just store index 4.
Stored Indices: [2,3,4]
Answer Array: [1,1,0,0,0,0,0,0]
Step 6: Current Element → temperatures[5] = 72
72 > 69 → next warmer day for index 4 is index 5.
Update answer[4] = 5 - 4 = 1; remove 4.
72 > 71 → next warmer day for index 3 is index 5.
Update answer[3] = 5 - 3 = 2; remove 3.
72 < 75 → stop here.
Store index 5.
Stored Indices: [2,5]
Answer Array: [1,1,0,2,1,0,0,0]
Step 7: Current Element → temperatures[6] = 76
76 > 72 → next warmer day for index 5 is index 6.
Update answer[5] = 6 - 5 = 1; remove 5.
76 > 75 → next warmer day for index 2 is index 6.
Update answer[2] = 6 - 2 = 4; remove 2.
Store index 6.
Stored Indices: [6]
Answer Array: [1,1,4,2,1,1,0,0]
Step 8: Current Element → temperatures[7] = 73
73 < 76 → just store index 7.
Stored Indices: [6,7]
Answer Array: [1,1,4,2,1,1,0,0]
Remaining elements in stack: indices 6 and 7 → no warmer temperature appears afterward → keep answer[6] and answer[7] as 0.
Final Stored Indices: [6,7]
Final Answer: [1,1,4,2,1,1,0,0]
Since the waiting days are tracked in Last In, First Out order, the natural data structure to use here is a Stack.
Approach
Step 1: Initialize the answer array
Create an array answer of the same length as the input temperatures array.
Set all elements initially to 0.
This array will store, for each day, the number of days we have to wait to get a warmer temperature.
Step 2: Initialize an empty stack to keep track of indices
Create an empty stack to store the indices of days whose next warmer day hasn’t been found yet.
We will use this stack to keep track of waiting days.
Step 3: Loop through each day from start to end
Use a single loop where index i ranges from 0 to n - 1 (where n is the length of temperatures).
This picks each day one by one to check if it can help resolve previous waiting days in the stack.
Step 4: While current temperature is higher than the temperature at the index on top of the stack
Inside the loop, as long as the stack is not empty and
temperatures[i] > temperatures[stack top],
it means we’ve found the next warmer day for the day at index stack top.
Step 5: Pop from stack and update answer
Pop the index prevIndex from the stack.
Compute i - prevIndex, which is the number of days waited to get a warmer day.
Set answer[prevIndex] = i - prevIndex.
Step 6: After checking, push current index i into the stack
After resolving all previous days that now have a warmer temperature,
push the current day’s index i into the stack.
This means day i itself is now waiting for its next warmer day.
Step 7: Return the answer array
After the loop completes, return the answer array.
Remaining indices in the stack have no warmer day ahead, so their answer remains 0.
Dry Run
Let’s do a detailed dry run of the stack-based optimal approach
for the input:
temperatures = [73,74,75,71,69,72,76,73]
We want to build the answer array where for each day, we find how many days we have to wait to get a warmer temperature.
Step 1: Initialize answer array
Create answer = [0,0,0,0,0,0,0,0]
Length of temperatures, n = 8
Also initialize an empty stack to keep track of indices: stack = []
Iteration-wise Dry Run
i = 0 (temperature = 73)
stack is empty → push index 0
stack: [0]
i = 1 (temperature = 74)
Compare 74 > 73 → found warmer day for index 0
Pop 0 from stack → answer[0] = 1 - 0 = 1
stack: []
Push current index 1
stack: [1]
Current answer: [1,0,0,0,0,0,0,0]
i = 2 (temperature = 75)
75 > 74 → found warmer day for index 1
Pop 1 → answer[1] = 2 - 1 = 1
stack: []
Push index 2
stack: [2]
Current answer: [1,1,0,0,0,0,0,0]
i = 3 (temperature = 71)
75 > 71 → no warmer day yet
Push index 3
stack: [2,3]
i = 4 (temperature = 69)
71 > 69 → no warmer day yet
Push index 4
stack: [2,3,4]
i = 5 (temperature = 72)
72 > 69 → found warmer day for index 4
Pop 4 → answer[4] = 5 - 4 = 1
stack: [2,3]
72 > 71 → found warmer day for index 3
Pop 3 → answer[3] = 5 - 3 = 2
stack: [2]
72 < 75 → stop here
Push index 5
stack: [2,5]
Current answer: [1,1,0,2,1,0,0,0]
i = 6 (temperature = 76)
76 > 72 → found warmer day for index 5
Pop 5 → answer[5] = 6 - 5 = 1
stack: [2]
76 > 75 → found warmer day for index 2
Pop 2 → answer[2] = 6 - 2 = 4
stack: []
Push index 6
stack: [6]
Current answer: [1,1,4,2,1,1,0,0]
i = 7 (temperature = 73)
73 < 76 → no warmer day yet
Push index 7
stack: [6,7]
No more elements
Remaining indices in stack (6 and 7) don’t have a warmer day in the future → answer remains 0
Final Result
answer = [1,1,4,2,1,1,0,0]
Meaning:
- Day 0: wait 1 day to get warmer temperature
- Day 1: wait 1 day
- Day 2: wait 4 days
- Day 3: wait 2 days
- Day 4: wait 1 day
- Day 5: wait 1 day
- Day 6 & 7: no warmer temperature in future → 0
Code for All Languages
C++
#include <iostream> // For input and output functions like cin and cout
#include <vector> // For using the vector data structure
#include <stack> // For using the stack data structure
using namespace std;
class Solution {
public:
vector<int> dailyTemperatures(vector<int>& temperatures) {
int n = temperatures.size(); // Number of days
// Step 1: Initialize the answer array
vector<int> answer(n, 0); // Initially fill with zeros
// Step 2: Initialize a stack to store indices of days waiting for warmer temperatures
stack<int> st;
// Step 3: Traverse each day from left to right
for (int i = 0; i < n; i++) {
// Step 4: While the current temperature is warmer than the temperature at index on top of stack
while (!st.empty() && temperatures[i] > temperatures[st.top()]) {
// Step 5: Pop the index and update the answer for that day
int prevIndex = st.top();
st.pop();
answer[prevIndex] = i - prevIndex;
}
// Step 6: Push the current index to the stack
st.push(i);
}
// Step 7: Return the answer array as the required value
return answer;
}
};
int main() {
int n;
cin >> n; // Input number of days
vector<int> temperatures(n);
// Input the temperatures
for (int i = 0; i < n; i++) {
cin >> temperatures[i];
}
Solution sol;
vector<int> result = sol.dailyTemperatures(temperatures);
// Output the result
for (int days : result) {
cout << days << " ";
}
return 0;
}
Java
import java.util.*; // For Scanner, Stack, and Arrays
class Solution {
public int[] dailyTemperatures(int[] temperatures) {
int n = temperatures.length; // Number of days
// Step 1: Initialize the answer array
int[] answer = new int[n]; // By default, filled with zeros
// Step 2: Initialize a stack to store indices of days waiting for warmer temperatures
Stack<Integer> st = new Stack<>();
// Step 3: Traverse each day from left to right
for (int i = 0; i < n; i++) {
// Step 4: While current temperature is warmer than temperature at index on top of stack
while (!st.isEmpty() && temperatures[i] > temperatures[st.peek()]) {
// Step 5: Pop the index and update the answer for that day
int prevIndex = st.pop();
answer[prevIndex] = i - prevIndex;
}
// Step 6: Push the current index to the stack
st.push(i);
}
// Step 7: Return the answer array as the required value
return answer;
}
}
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
// Input number of days
int n = sc.nextInt();
int[] temperatures = new int[n];
// Input the temperatures
for (int i = 0; i < n; i++) {
temperatures[i] = sc.nextInt();
}
Solution sol = new Solution();
int[] result = sol.dailyTemperatures(temperatures);
// Output the result
for (int days : result) {
System.out.print(days + " ");
}
}
}Python
from typing import List # For specifying type hints
class Solution:
def dailyTemperatures(self, temperatures: List[int]) -> List[int]:
n = len(temperatures) # Number of days
# Step 1: Initialize the answer list
answer = [0] * n # By default, filled with zeros
# Step 2: Initialize a stack to store indices of days waiting for warmer temperatures
stack = []
# Step 3: Traverse each day from left to right
for i in range(n):
# Step 4: While current temperature is warmer than temperature at index on top of stack
while stack and temperatures[i] > temperatures[stack[-1]]:
# Step 5: Pop the index and update the answer for that day
prev_index = stack.pop()
answer[prev_index] = i - prev_index
# Step 6: Push the current index to the stack
stack.append(i)
# Step 7: Return the answer list as the required value
return answer
if __name__ == "__main__":
# Input number of days
n = int(input())
# Input the temperatures
temperatures = list(map(int, input().split()))
sol = Solution()
result = sol.dailyTemperatures(temperatures)
# Output the result
print(' '.join(map(str, result)))
Javascript
/**
* @param {number[]} temperatures
* @return {number[]}
*/
var dailyTemperatures = function(temperatures) {
const n = temperatures.length; // Number of days
// Step 1: Initialize the answer array
const answer = Array(n).fill(0); // Default is 0 for each day
// Step 2: Initialize a stack to store indices of days waiting for warmer temperatures
const stack = [];
// Step 3: Traverse each day from left to right
for (let i = 0; i < n; i++) {
// Step 4: While current temperature is warmer than temperature at index on top of stack
while (stack.length > 0 && temperatures[i] > temperatures[stack[stack.length - 1]]) {
// Step 5: Pop the index and update the answer for that day
const prevIndex = stack.pop();
answer[prevIndex] = i - prevIndex;
}
// Step 6: Push the current index to the stack
stack.push(i);
}
// Step 7: Return the answer array as the required value
return answer;
};
// Driver code
const readline = require("readline");
const rl = readline.createInterface({
input: process.stdin,
output: process.stdout
});
let inputs = [];
let n;
rl.on("line", function(line) {
inputs.push(line.trim());
if (inputs.length === 2) {
// First line: number of days
n = parseInt(inputs[0]);
// Second line: list of temperatures
const temperatures = inputs[1].split(' ').map(Number);
const result = dailyTemperatures(temperatures);
console.log(result.join(' '));
rl.close();
}
});
Time Complexity: O(n)
Let’s denote: n = length of the array temperatures.
Outer Loop: O(n)
– We traverse the array from left to right once using index i.
– So, the outer loop itself runs exactly n times.
Inner Process (while loop with stack): Amortized O(1) per element
– For each temperature, we may pop elements from the stack.
– Each element is pushed to the stack exactly once and popped exactly once.
– So across all n elements, the total number of stack operations (push + pop) is at most 2n.
Total Time per Outer Loop Iteration: O(1) amortized
– Because each pop/push happens only once per element across the entire traversal.
Final Time Complexity: O(n)
Adding it all together:
– The outer loop runs n times.
– The inner stack operations cost amortized O(1) per element.
So, the total complexity becomes: O(n) × O(1) = O(n).
Space Complexity: O(n)
Auxiliary Space Complexity: O(n)
This refers to the extra space used by the algorithm beyond the input itself.
In our optimal stack-based approach, we create:
– An answer array of length n to store the number of days until a warmer temperature → O(n).
– A stack that, in the worst case, could store up to n indices → O(n).
Other than that, we only use a few integer variables for loop counters and temporary values → O(1).
So, the auxiliary space complexity becomes O(n + n) = O(n).
Total Space Complexity: O(n)
This includes:
– Input space: the input array temperatures of length n → O(n).
– Output space: the answer array of length n → O(n).
– Extra space: the stack as analyzed above → O(n).
Combining all these, the overall total space complexity remains O(n).
Key Takeaways
The technique of using a stack with a monotonic property (either increasing or decreasing) is often referred to as a Monotonic stack. Many problems can be efficiently solved using this approach, so it is important to become familiar with it.
What is a Monotonic Stack?
The monotonic stack approach revolves around utilizing a stack data structure to solve specific types of problems efficiently.
It is based on the idea of maintaining a monotonic property, either increasing or decreasing, while processing the elements of an array or sequence.
Monotonic Increasing Stack
- The elements in the stack are maintained in increasing order.
- When processing a new element, you pop elements from the stack until you find an element smaller than the current element.
Monotonic Decreasing Stack:
- The elements in the stack are maintained in decreasing order.
- When processing a new element, you pop elements from the stack until you find an element larger than the current element.
Why Use a Monotonic Stack?
The monotonic stack is a powerful use stack, particularly for problems involving comparisons or ranges within a sequence. Here are some key reasons to use it:
- The monotonic stack allows certain types of problems to be solved in linear time, O(n). This is because each element is pushed and popped from the stack at most once.
- It simplifies the logic for problems involving finding the next/previous greater/smaller elements. Instead of using nested loops which can be complex and inefficient, a single pass with a stack suffices.
- It can be applied to a variety of problems in different domains, such as arrays, histograms, and even strings.
Learning Tip
Since we have solved the Next Greater Element problem, let’s now tackle the following related problems:
You are given two distinct 0-indexed integer arrays nums1 and nums2, where nums1 is a subset of nums2. For each 0 <= i < nums1.length, find the index j such that nums1[i] == nums2[j] and determine the next greater element of nums2[j] in nums2. If there is no next greater element, then the answer for this query is -1.
Return an array ans of length nums1.length such that ans[i] is the next greater element as described above.