Count the Number of Beautiful Subarrays Solution In C++/Java/Python/JS
Problem Description
You are given a 0-indexed integer array nums. In one operation, you can:
Choose two different indices i and j such that 0 <= i, j < nums.length.
Choose a non-negative integer k such that the kth bit (0-indexed) in the binary representation of nums[i] and nums[j] is 1 .
Subtract 2^k from nums[i] and nums[j].
A subarray is beautiful if it is possible to make all of its elements equal to 0 after applying the above operation any number of times (including zero).
Return the number of beautiful subarrays in the array nums.
What is a Subarray?
A subarray is a contiguous non-empty sequence of elements within an array.
Note: Subarrays where all elements are initially 0 are considered beautiful, as no operation is needed.
Examples
Input: matrix = [[0,1,0],[1,1,1],[0,1,0]], target = 0
Output: 4
Explanation: The four 1x1 submatrices that only contain 0.
Input: matrix = [[1,-1],[-1,1]], target = 0
Output: 5
Explanation: The two 1x2 submatrices, plus the two 2x1 submatrices, plus the 2x2 submatrix.
Input: matrix = [[904]], target = 0
Output: 0
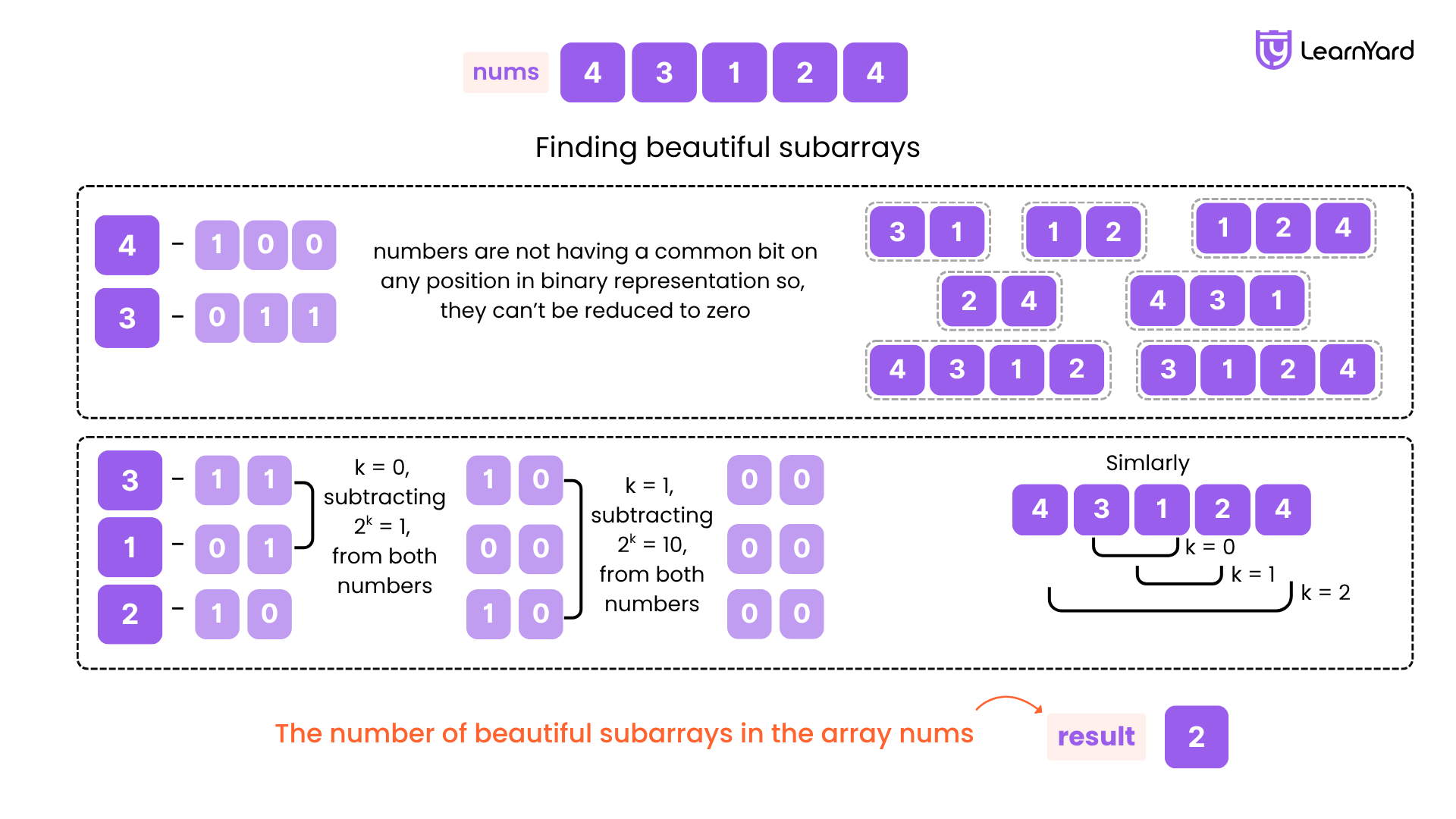
Input: nums = [4,3,1,2,4]
Output: 2
Explanation: There are 2 beautiful subarrays in nums: [4,3,1,2,4] and [4,3,1,2,4].
- We can make all elements in the subarray [3,1,2] equal to 0 in the following way:
- Choose [3, 1, 2] and k = 1. Subtract 21 from both numbers. The subarray becomes [1, 1, 0].
- Choose [1, 1, 0] and k = 0. Subtract 20 from both numbers. The subarray becomes [0, 0, 0].
- We can make all elements in the subarray [4,3,1,2,4] equal to 0 in the following way:
- Choose [4, 3, 1, 2, 4] and k = 2. Subtract 22 from both numbers. The subarray becomes [0, 3, 1, 2, 0].
- Choose [0, 3, 1, 2, 0] and k = 0. Subtract 20 from both numbers. The subarray becomes [0, 2, 0, 2, 0].
- Choose [0, 2, 0, 2, 0] and k = 1. Subtract 21 from both numbers. The subarray becomes [0, 0, 0, 0, 0].
Input: nums = [1,10,4]
Output: 0
Explanation: There are no beautiful subarrays in nums.
Constraints
- 1 <= nums.length <= 10^5
- 0 <= nums[i] <= 10^6
The very first question that comes to our mind after reading the problem is: How can we efficiently count the number of beautiful subarrays in the given array? Most of us already know that one straightforward way is to generate all possible subarrays of the array and check whether each satisfies the condition that it can be reduced to all zeros using the allowed operation. To build a solid understanding, let’s start by exploring this brute-force approach in detail. This will help us grasp the core concept of what makes a subarray “beautiful” and how the bitwise properties of its elements determine whether the operation can zero them out completely.
Brute Force Approach
Intuition
Since we want to find all subarrays in nums that are beautiful, the first idea that comes to our mind is to generate all possible subarrays of nums and check whether each satisfies the condition that all its elements can be made zero using the given bitwise operation.
For example, if nums has length n, then we can go through the array and take out every possible subarray starting from each index.
Generating All Subarrays using Nested Loops
To implement this, we first fix the starting index i of the subarray in nums using an outer loop. This loop runs from i = 0 up to i = nums.length - 1, ensuring that every possible starting point for a subarray is covered.
For each fixed starting index i, we use an inner loop with index j to manually build the subarray by expanding its end point. This inner loop runs from j = i up to j < nums.length. At each step, the subarray extends by including nums[j]. This manual expansion shows beginners how to form subarrays using simple index logic without relying on built-in slicing functions.
Let’s consider an example to clarify this process. Suppose nums = [4, 3, 1, 2, 4]. Using the loops:
At i = 0, the inner loop builds subarrays [4], [4, 3], [4, 3, 1], [4, 3, 1, 2], [4, 3, 1, 2, 4]
At i = 1, the inner loop builds [3], [3, 1], [3, 1, 2], [3, 1, 2, 4]
At i = 2, the inner loop builds [1], [1, 2], [1, 2, 4]
At i = 3, the inner loop builds [2], [2, 4]
At i = 4, the inner loop builds [4]
Each subarray is a contiguous sequence starting at i and ending at j.
Once we have a subarray from nums, now we need to check if it is beautiful.
Checking If the Subarray is Beautiful
Once we have generated a subarray using our nested loops, the next step is to decide whether this subarray is beautiful or not. According to the problem statement, a subarray is beautiful if it is possible to make all of its numbers equal to 0 by repeatedly using the given pairwise bit operation.
Making all the numbers in the subarray means that, all the bits of all the numbers in the subarray should be unset. (0)
At first glance, this may feel confusing: How do we know if we can really remove all bits from every number using the allowed operations? To build our understanding, let’s break it down:
The operation lets us choose any two numbers in the subarray and pick any bit position k where both numbers have a 1. Then, we can subtract 2^k from both numbers. What does that do?
Since the bit at position k adds 2^k to the value of the number, it is same as turning that 1 bit off in both numbers at the same time.
Now since we want to make all the numbers in the subarray 0, and each operation needs two numbers where any bit k is 1 in both. So to remove all the bits at a particular position from all the numbers in the subarray, it should hold that
there are an even number of 1s at that bit position. Why? Because each operation removes that bit from two numbers at a time — so every 1 must have a matching pair.
This gives us an important insight: For a subarray to be beautiful, the total count of 1's at every bit position must be even. If any bit position has an odd number of 1's, there will be one leftover 1 that cannot be paired and removed, so we can’t reduce the whole subarray to 0.
So , for each subarray we need to count the number of 1's at every bit position and check if for all the bit positions, is this count even? If yes, then the subarray is beautiful else not.
Now how many bit positions do we need to check?
Since the problem states that each number nums[i] can be at most 1,000,000, we can find the maximum number of bits needed to represent any number up to 1,000,000 in binary.
The binary representation of 1,000,000 is slightly less than 2^{20}.
This means we only need to track bit positions 0 to 19.
Keeping a Track of Bit Counts
To keep track of how many 1s appear at each bit position within the current subarray, we can create a frequency array of size 20.
What is a Frequency Array?
A frequency array is just a way to count how many times each element appears — usually characters in a string or numbers in a specific range.
Think of it as a table or list that keeps track of how often each item shows up.
Let’s call this array bitCount of size 20.
bitCount[0] will store how many numbers in the subarray have a 1 at bit position 0.
bitCount[1] will store how many have a 1 at bit position 1, and so on.
So, for each subarray:
- We initialize a fresh bitCount array of size 20 with all zeros.
- Then, as we add each number to the subarray (in the inner loop), we check each of its 20 bits:
For every bit position k from 0 to 19:
If that bit is set (1), in the current number, we increment bitCount[k] by 1.
Checking if a Bit at a Particular Position is Set
How to check if the kth bit in a number is 1?
The simple trick is to shift the number 1 to the left by k places, and then check with the AND operator.
- First, shift 1 to the left by k places: 1 << k
This makes a number that has o0nly the kth bit as 1, and all other bits as 0.
- Then, use the AND operator (&) to check: num & (1 << k)
If this is not zero, it means the kth bit in num is 1.
If this is zero, it means the kth bit in num is 0.
Example
Let’s say num = 5 → binary: 101
Check if the 0th bit is 1:
1 << 0 = 1 → 5 & 1 = 101 & 001 = 001 → not zero → so the 0th bit is 1.
Check if the 1st bit is 1:
1 << 1 = 2 → binary 010 → 5 & 2 = 101 & 010 = 000 → zero → so the 1st bit is 0.
Check if the 2nd bit is 1:
1 << 2 = 4 → binary 100 → 5 & 4 = 101 & 100 = 100 → not zero → so the 2nd bit is 1.
Key Point:
If num & (1 << k) is not zero, the kth bit is 1. If it is zero, the kth bit is 0.
- After processing the entire subarray, we check if all the entries in bitCount are even.
If every bitCount[k] is even, this subarray is beautiful, so add 1 to a variable ans that would store the final result.
If any position has an odd count, this subarray cannot be reduced to 0.
Finally return the variable ans.
Approach
Step 1: Initialize variable ans
Create a variable ans to store the total count of beautiful subarrays.
Initially set ans = 0.
Step 2: Use an outer loop to fix the starting index i of the subarray.
Run a loop i from 0 to n - 1, where n is the length of nums.
Step 3: For each subarray, initialize a frequency array.
Create an array bitCount of size 20 and set all its elements to 0.
This array keeps track of how many 1s appear at each bit position in the current subarray.
Step 4: Use an inner loop to fix the ending index j of the subarray.
For each i, run another loop j from i to n - 1.
This way, you cover all possible subarrays starting at i.
Step 5: Loop for every bit position of current number and update bitCount:
For every bit position k from 0 to 19:
If the kth bit in nums[j] is 1, increment bitCount[k] by 1.
Step 6: Run a Loop for every bit position
Set a Boolean variable isBeautiful to true (indicating subarray is beautiful)
loop through k = 0 to 19.
Go through each position k in bitCount.
Step 7: Break if a subarray is not beautiful
If any bitCount[k] is odd, this means there’s an unpaired bit → subarray is not beautiful, set isBeautiful to false and break.
As soon as you find an odd count, stop checking further bits for this subarray.
Step 8: Increment ans if current subarray is beautiful
If all bitCount[k] are even, implying isBeautiful is true, then this subarray is beautiful → increment ans by 1.
If you don’t break in Step 7, then this subarray satisfies the condition.
Step 9: Return the final answer.
After all loops, return ans as the total count of beautiful subarrays.
Dry Run
Let’s do a detailed dry run of the brute-force approach using nested loops and a bit frequency array for the input:
nums = [4, 3, 1, 2, 4]
We want to count all subarrays where all bit positions (0–19) have an even count of 1’s so that the subarray can be reduced to 0.
Step 1: Initialization
Original array: nums = [4, 3, 1, 2, 4]
Length n = 5
ans = 0 → Will store the total count of beautiful subarrays
Step 2: Loop Over nums to Check All Possible Subarrays
Since the length of nums is 5, we want to check every possible subarray.
We run two nested loops:
The outer loop fixes the starting index i from 0 to n - 1.
For each fixed i, the inner loop runs from j = i to n - 1.
For every subarray [i..j]:
We update a frequency array bitCount of size 20.
We check if all counts are even to decide if it’s beautiful.
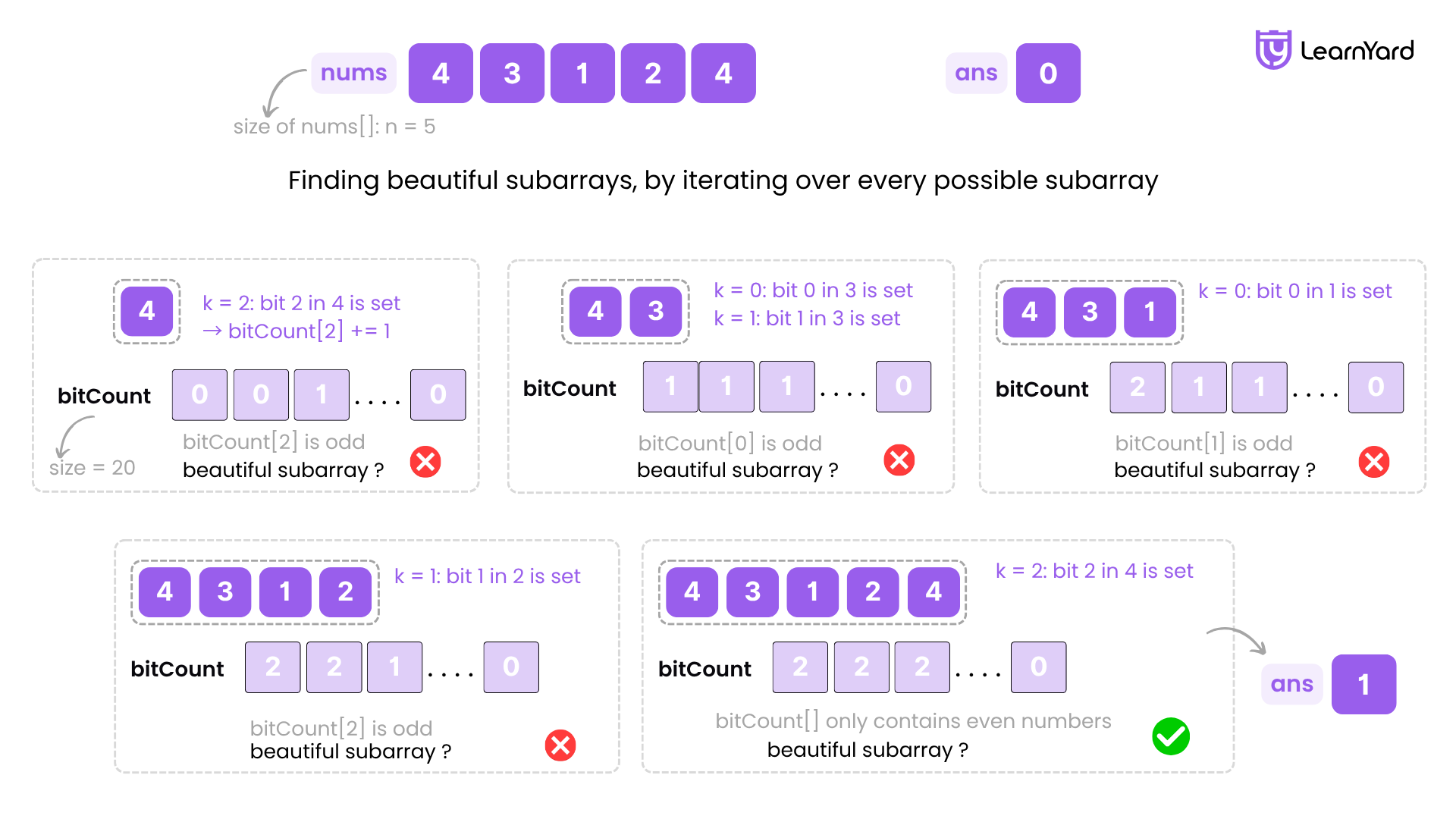
Iteration-Wise Dry Run
Outer Loop: i = 0
j = 0 → Subarray [4]
Step 4: Initialize bitCount → [0] * 20
Step 5: Loop k = 0 to 19:
k = 2: bit 2 in 4 is set → bitCount[2] += 1 → now bitCount = [0, 0, 1, ...]
Step 6: Check if all counts are even:
k = 2: 1 → odd → break
Step 7: Subarray not beautiful → ans unchanged
j = 1 → Subarray [4, 3]
k = 0: bit 0 in 3 is set → bitCount[0] += 1 → [1, 0, 1, ...]
k = 1: bit 1 in 3 is set → bitCount[1] += 1 → [1, 1, 1, ...]
Step 6:
k = 0: 1 → odd → break
Step 7: Not beautiful → ans unchanged
j = 2 → Subarray [4, 3, 1]
k = 0: bit 0 in 1 is set → bitCount[0] += 1 → [2, 1, 1, ...]
Step 6:
k = 0: 2 → even
k = 1: 1 → odd → break
Step 7: Not beautiful → ans unchanged
j = 3 → Subarray [4, 3, 1, 2]
k = 1: bit 1 in 2 is set → bitCount[1] += 1 → [2, 2, 1, ...]
Step 6:
k = 0: 2 → even
k = 1: 2 → even
k = 2: 1 → odd → break
Step 7: Not beautiful
j = 4 → Subarray [4, 3, 1, 2, 4]
k = 2: bit 2 in 4 is set → bitCount[2] += 1 → [2, 2, 2, ...]
Step 6:
k = 0: 2 → even
k = 1: 2 → even
k = 2: 2 → even
All others zero → all even
Step 8: Beautiful → ans += 1 → ans = 1
Outer Loop: i = 1
j = 1 → Subarray [3]
New bitCount → [0] * 20
nums[1] = 3
k = 0: set → [1, 0, ...]
k = 1: set → [1, 1, ...]
Step 6:
k = 0: 1 → odd → break
Step 7: Not beautiful
j = 2 → Subarray [3, 1]
nums[2] = 1
k = 0: set → [2, 1, ...]
Step 6:
k = 0: 2 → even
k = 1: 1 → odd → break
Step 7: Not beautiful
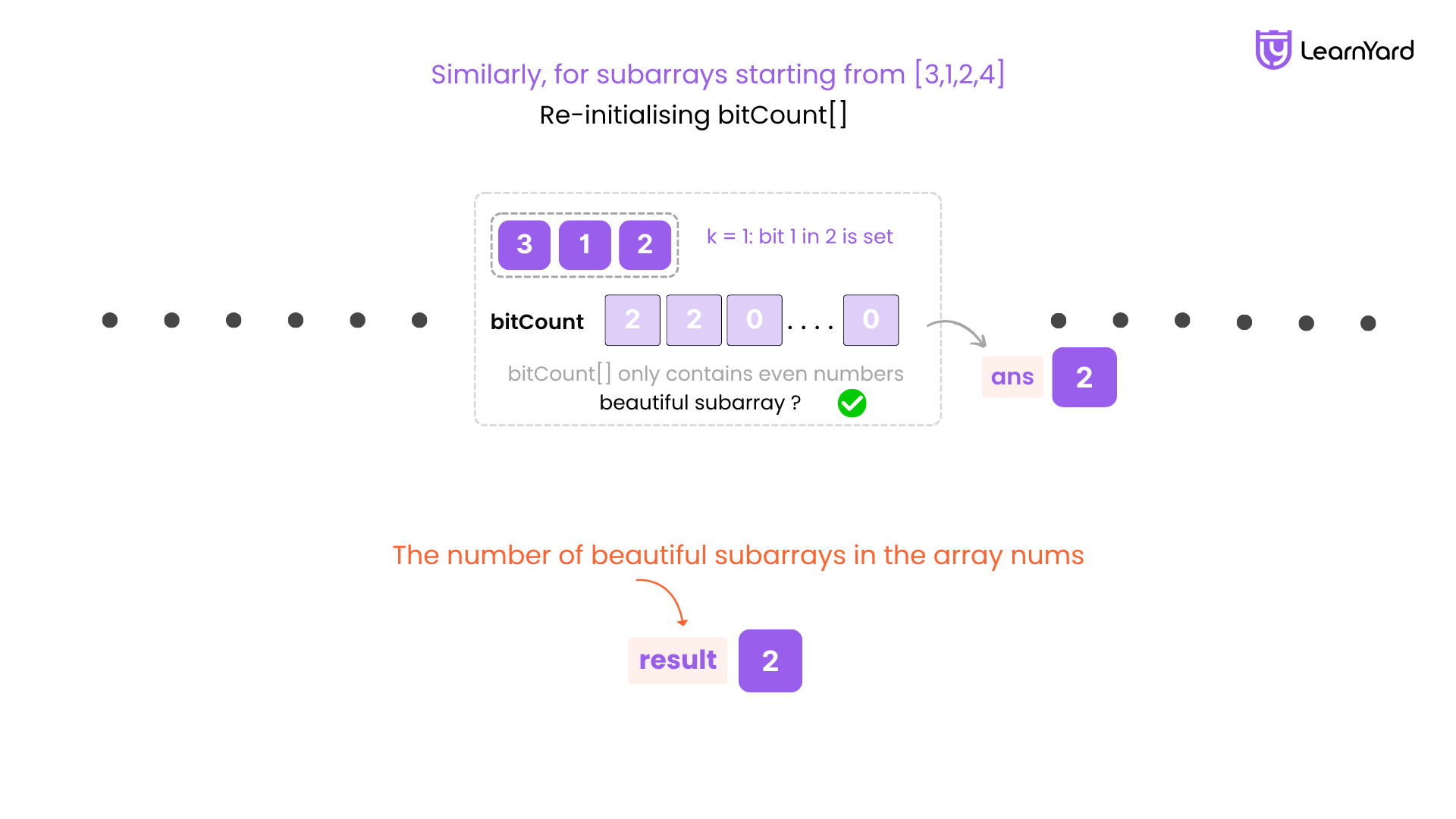
j = 3 → Subarray [3, 1, 2]
nums[3] = 2
k = 1: set → [2, 2, ...]
Step 6:
k = 0: 2 → even
k = 1: 2 → even
All others zero → all even
Step 8: Beautiful → ans += 1 → ans = 2
j = 4 → Subarray [3, 1, 2, 4]
nums[4] = 4
k = 2: set → [2, 2, 1, ...]
Step 6:
k = 0: 2 → even
k = 1: 2 → even
k = 2: 1 → odd → break
Step 7: Not beautiful
Outer Loop: i = 2
j = 2 → Subarray [1]
New bitCount → [0] * 20
nums[2] = 1
k = 0: set → [1, 0, ...]
Step 6:
k = 0: 1 → odd → break
Step 7: Not beautiful
j = 3 → Subarray [1, 2]
nums[3] = 2
k = 1: set → [1, 1, ...]
Step 6:
k = 0: 1 → odd → break
Step 7: Not beautiful
j = 4 → Subarray [1, 2, 4]
nums[4] = 4
k = 2: set → [1, 1, 1, ...]
Step 6:
k = 0: 1 → odd → break
Step 7: Not beautiful
Outer Loop: i = 3
j = 3 → Subarray [2]
New bitCount → [0] * 20
nums[3] = 2
k = 1: set → [0, 1, ...]
Step 6:
k = 1: 1 → odd → break
Step 7: Not beautiful
j = 4 → Subarray [2, 4]
nums[4] = 4
k = 2: set → [0, 1, 1, ...]
Step 6:
k = 1: 1 → odd → break
Step 7: Not beautiful
Outer Loop: i = 4
j = 4 → Subarray [4]
New bitCount → [0] * 20
nums[4] = 4
k = 2: set → [0, 0, 1, ...]
Step 6:
k = 2: 1 → odd → break
Step 7: Not beautiful
Final Step: Return ans = 2
So there are 2 beautiful subarrays in nums = [4, 3, 1, 2, 4].
Code for All Languages
C++
#include <iostream> // For input and output
#include <vector> // For using the vector data structure
using namespace std;
class Solution {
public:
long long beautifulSubarrays(vector<int>& nums) {
// Step 1: Initialize variable ans
long long ans = 0;
int n = nums.size();
// Step 2: Use an outer loop to fix the starting index i of the subarray
for (int i = 0; i < n; i++) {
// Step 3: For each subarray, initialize a frequency array
vector<int> bitCount(20, 0);
// Step 4: Use an inner loop to fix the ending index j of the subarray
for (int j = i; j < n; j++) {
// Step 5: Loop for every bit position of current number and update bitCount
for (int k = 0; k < 20; k++) {
if ((nums[j] >> k) & 1) {
bitCount[k]++;
}
}
// Step 6: Run a Loop for every bit position
bool isBeautiful = true;
for (int k = 0; k < 20; k++) {
// Step 7: Break if a subarray is not beautiful
if (bitCount[k] % 2 != 0) {
isBeautiful = false;
break;
}
}
// Step 8: Increment ans if current subarray is beautiful
if (isBeautiful) {
ans++;
}
}
}
// Step 9: Return the final answer
return ans;
}
};
int main() {
int n;
cin >> n;
vector<int> nums(n);
for (int i = 0; i < n; i++) {
cin >> nums[i];
}
Solution sol;
long long result = sol.beautifulSubarrays(nums); // Call the function
cout << result << endl; // Output the result
return 0;
}
Java
import java.util.*; // For Scanner and Arrays
class Solution {
public long beautifulSubarrays(int[] nums) {
// Step 1: Initialize variable ans
long ans = 0;
int n = nums.length;
// Step 2: Use an outer loop to fix the starting index i of the subarray
for (int i = 0; i < n; i++) {
// Step 3: For each subarray, initialize a frequency array
int[] bitCount = new int[20];
// Step 4: Use an inner loop to fix the ending index j of the subarray
for (int j = i; j < n; j++) {
// Step 5: Loop for every bit position of current number and update bitCount
for (int k = 0; k < 20; k++) {
if (((nums[j] >> k) & 1) == 1) {
bitCount[k]++;
}
}
// Step 6: Run a Loop for every bit position
boolean isBeautiful = true;
for (int k = 0; k < 20; k++) {
// Step 7: Break if a subarray is not beautiful
if (bitCount[k] % 2 != 0) {
isBeautiful = false;
break;
}
}
// Step 8: Increment ans if current subarray is beautiful
if (isBeautiful) {
ans++;
}
}
}
// Step 9: Return the final answer
return ans;
}
}
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
int[] nums = new int[n];
for (int i = 0; i < n; i++) {
nums[i] = sc.nextInt();
}
Solution sol = new Solution();
long result = sol.beautifulSubarrays(nums); // Call the function
System.out.println(result); // Output the result
}
}
Python
from typing import List #for input handling
class Solution:
def beautifulSubarrays(self, nums: List[int]) -> int:
# Step 1: Initialize variable ans
ans = 0
n = len(nums)
# Step 2: Use an outer loop to fix the starting index i of the subarray
for i in range(n):
# Step 3: For each subarray, initialize a frequency array
bitCount = [0] * 20
# Step 4: Use an inner loop to fix the ending index j of the subarray
for j in range(i, n):
# Step 5: Loop for every bit position of current number and update bitCount
for k in range(20):
if (nums[j] >> k) & 1:
bitCount[k] += 1
# Step 6: Run a Loop for every bit position
isBeautiful = True
for k in range(20):
# Step 7: Break if a subarray is not beautiful
if bitCount[k] % 2 != 0:
isBeautiful = False
break
# Step 8: Increment ans if current subarray is beautiful
if isBeautiful:
ans += 1
# Step 9: Return the final answer
return ans
if __name__ == "__main__":
n = int(input())
nums = list(map(int, input().split())) # Input the list
sol = Solution()
result = sol.beautifulSubarrays(nums) # Call the function
print(result) #Print the result
Javascript
/**
* @param {number[]} nums - The input array of integers
* @return {number} - Total number of beautiful subarrays
*/
var beautifulSubarrays = function(nums) {
// Step 1: Initialize variable ans
let ans = 0;
const n = nums.length;
// Step 2: Use an outer loop to fix the starting index i of the subarray
for (let i = 0; i < n; i++) {
// Step 3: For each subarray, initialize a frequency array
let bitCount = new Array(20).fill(0);
// Step 4: Use an inner loop to fix the ending index j of the subarray
for (let j = i; j < n; j++) {
// Step 5: Loop for every bit position of current number and update bitCount
for (let k = 0; k < 20; k++) {
if ((nums[j] >> k) & 1) {
bitCount[k]++;
}
}
// Step 6: Run a Loop for every bit position
let isBeautiful = true;
for (let k = 0; k < 20; k++) {
// Step 7: Break if a subarray is not beautiful
if (bitCount[k] % 2 !== 0) {
isBeautiful = false;
break;
}
}
// Step 8: Increment ans if current subarray is beautiful
if (isBeautiful) {
ans++;
}
}
}
// Step 9: Return the final answer
return ans;
};
// Driver code
const readline = require("readline");
const rl = readline.createInterface({
input: process.stdin,
output: process.stdout
});
let inputs = [];
rl.on("line", function(line) {
inputs.push(line.trim());
if (inputs.length === 2) {
const nums = inputs[1].split(' ').map(Number);
const result = beautifulSubarrays(nums);
console.log(result);
rl.close();
}
});Time Complexity: O(n²)
Let us denote:
- n = length of nums
- k = number of bit positions (20 here)
The outer loop runs O(n) times.
Outer Loop: O(n)
The outer loop runs from i = 0 to i = n - 1.
Inner Loop: O(n)
For each outer loop iteration, the inner loop runs from j = i to n - 1.
In the worst case, this loop does O(n) work per i.
Updating bitCount and Checking: O(k)
Inside the inner loop:
- Updating bitCount takes O(k) for k = 0 to 19.
- Checking if all bitCount values are even takes another O(k).
Since k = 20 is constant:
O(k) = O(1).
Total per Inner Loop Iteration: O(1)
So each (i, j) pair costs O(1) time.
Final Time Complexity: O(n²)
- Outer loop: O(n)
- Inner loop: O(n)
- Work per pair: O(1)
So, the overall time complexity is: O(n) * O(n) * O(1) = O(n²)
Space Complexity: O(1)
Auxiliary Space Complexity: O(1)
This refers to any extra space used by the algorithm that is independent of the input and output space. In our brute-force approach, we create:
A bitCount array of size 20 for each subarray.
A Boolean flag isBeautiful to check if a subarray is beautiful.
Since the size of bitCount is fixed at 20 bits, its contribution is constant: O(1). No other significant extra data structures are used that grow with n.
Total Space Complexity: O(n)
Input space: The input array nums of length n → O(n).
Output space: The variable ans to store the final count → O(1).
Extra space: The bitCount array → O(1).
Putting it all together:
Total Space Complexity = O(n) + O(1) = O(n)
Will brute force work against the given constraints?
For the current solution, the time complexity is O(n²), which is not suitable for n ≤ 10⁵. This means that for each test case, where the length of the array is at most 10⁵, the solution might not execute within the given time limits.
Since O(n²) results in a maximum of 10¹⁰ operations (for n = 10⁵), the solution is not expected to work well for larger test cases. In most competitive programming environments, problems can handle up to 10⁶ operations per test case, meaning that for n ≤ 10⁵, the solution with 10¹⁰ operations is not efficient enough.
When multiple test cases are involved, the total number of operations could easily exceed this limit and approach 10¹⁰ operations, especially when there are many test cases or the value of n increases.
Thus, while the solution meets the time limits for a single test case, the O(n²) time complexity poses a risk for Time Limit Exceeded (TLE) errors when handling larger input sizes or multiple test cases. This can be a challenge for competitive programming problems with larger inputs or numerous test cases.
The brute-force approach checks every subarray and counts bits, but nested loops make it too slow. Instead of checking each subarray bit by bit, can we track how bit patterns evolve? Using prefix XORs can help skip redundant checks and speed up the solution.
Let’s explore this smarter approach.
Optimal Approach
Intuition
If you observe closely, the goal is to find subarrays where the number of set bits at every position (from bit 0 to bit 19) is even.
But what does it actually mean for every bit to appear an even number of times across the subarray?
Let’s pause and think carefully:
Suppose we pick a small subarray, say nums = [2, 2].
In binary, 2 = 10.
Let’s count the set bits at each position:
- At bit position 1 (the second bit from the right), both numbers have it set → total count = 2 (even).
- At bit position 0 (rightmost bit), both numbers have it unset → total count = 0 (even).
Since every bit position has an even count of set bits, this subarray is beautiful.
But notice something interesting:
If we XOR the numbers together:
2 ^ 2 = 0
What is XOR?
XOR (exclusive OR) is a bitwise operation that follows a simple rule:
0 ^ 0 = 0
1 ^ 0 = 1
0 ^ 1 = 1
1 ^ 1 = 0
In simple terms, XOR outputs 1 if the two bits are different, and 0 if they are the same.
Why is XOR interesting?
- When you XOR the same number with itself, you get 0 (e.g., 5 ^ 5 = 0).
- When you XOR any number with 0, it remains unchanged (e.g., 7 ^ 0 = 7).
The result is 0 because each set bit cancels itself out.
That’s the magic of XOR:
- when a bit appears an even number of times, it cancels to 0.
- when a bit appears an odd number of times, it remains 1.
So If we try to find the XOR of all the numbers in a subarray, then each bit that appears an even number of times across a subarray simply cancels out and becomes 0 in the final XOR.
For a subarray to be considered beautiful, every bit position should have an even count of set bits, implying that in the XOR value of all the numbers in that subarray, each bit position should be 0, leading to a decimal value of 0.
That’s the key observation:
- subarray XOR = 0 → means all bits cancel out
- → means every bit position has an even count of 1’s
- → which matches our definition of a beautiful subarray.
That’s why instead of explicitly counting the number of set bits in every subarray,
we can simply check if the XOR of the subarray is 0.
If yes, it must be beautiful.
So the problem boils down to finding the number of subarrays in nums with XOR=0.
At this point, we might think — let’s generate all subarrays, compute the XOR for each one, and check if XOR is zero.
But that would still be O(n²) because of the need to generate all the subarrays, which is too slow for large n.
So How do we Optimize this?
If you observe closely, the goal is to find the subarray XOR efficiently.
To do this, we need an approach to find the XOR of the subarray from the
starting point i to the ending point j in the array nums.
Yes, there is an approach to this. If we store the cumulative XOR from index 0 to index i, we can easily know the XOR up to the i-th index.
This cumulative XOR is often referred to as the prefix XOR.
So let's take an array nums = [4, 3, 1, 2, 4]
prefixXOR(nums) = [4, 7, 6, 4, 0]
Assuming 0-based indexing:
- At index 0: XOR = 4
- At index 1: XOR = 4 ^ 3 = 7
- At index 2: XOR = 4 ^ 3 ^ 1 = 6
- At index 3: XOR = 4 ^ 3 ^ 1 ^ 2 = 4
- At index 4: XOR = 4 ^ 3 ^ 1 ^ 2 ^ 4 = 0
So now we know how to find out the prefix XOR till the i-th index, but the problem is we need to find the subarray XOR from index i to index j, so how will we find it?
Let’s use the same example again: nums = [4, 3, 1, 2, 4]
prefixXOR(nums) = [4, 7, 6, 4, 0]
Let’s say we need to find a subarray XOR starting at index i and ending at index j.
Let’s take the example i = 1, j = 3.
So here we know:
- prefixXOR[i-1] = prefixXOR[0] = 4
- prefixXOR[j] = prefixXOR[3] = 4
To find the XOR of the subarray from i to j,
i.e., subarray(nums[i_to_j]), we will simply XOR prefixXOR[i-1] with prefixXOR[j].
Why i - 1? Because we want to exclude nums[0...i-1] and only include nums[i...j].
So:
- prefixXOR[0] = 4
- prefixXOR[3] = 4
The subarray XOR (nums[i_to_j]) is calculated as:
prefixXOR[j] ^ prefixXOR[i-1] = 4 ^ 4 = 0
When the result is 0, it means the subarray nums[i..j] is beautiful
So in general if we need to find out the subarray XOR from index i to j
we will get our answer as prefixXOR[j]^prefixXOR[i-1] (where i-1,j≥0).
What if i=0, i-1 will become negative?
Then the subarray XOR will be prefixXOR[j] i.e. a subarray starting with index 0 and ending at index j.
But now we need to count how many beautiful subarrays exist.
Let’s observe the prefix XOR equation closely:
prefixXOR[j] ^ prefixXOR[i-1] = 0
→ prefixXOR[j] = prefixXOR[i-1]
So for every j, we need to find how many prefixXOR[i-1] equal to prefixXOR[j] exist among previous indices.
But if for every j we run a loop from 0 to j-1, it will again take us to approx. O(n) for each j → total n² operations.
To optimize this, what if we use a data structure through which we get the count of prefixXOR[i-1] == prefixXOR[j] in O(1)?
Yes, you’re right! We could use something like a hash table to store the count of each prefixXOR as we go through the array.
What is Hash Table?
A hashtable is a data structure that stores key-value pairs, using a hash function to compute an index for quick access. It offers average O(1) time complexity for operations like insertion, deletion, and lookup.
But wait — our prefixXOR values can go up to about 2^20 (since numbers are less than about 10^6, which fits in 20 bits).
Building a hash table large enough for every possible XOR would be wasteful.
So, how do we tackle this?
The answer is hash maps.
Unlike arrays or fixed-size tables, a hash map dynamically stores only the XOR values we actually encounter, along with their counts.
This way, we avoid wasting memory on XOR values that never appear, making the solution both space-efficient and fast.
What are HashMap's?
Hash maps are a powerful data structure that store key-value pairs, allowing for fast access to values using their keys. They are used to determine where to store each pair, enabling average-case time complexities of O(1) for insertion, search, and deletion.
So for each index j, we only need the count of prefixXOR[i-1] that equals prefixXOR[j].
To do this, at every iteration we add the current prefixXOR[j] to our hash map, so it can be matched by future subarrays.
But wait!
What about subarrays that start at index i=0?
Let’s see why we need to initialize our map carefully.
nums = [4]
prefixXOR(nums) = [4]
If prefixXOR[j] itself is 0, it means the subarray from index 0 to j is beautiful (XOR is 0).
To count such subarrays starting at index 0 correctly, we initially hash 0 into our map as having occurred once.
So:
mp = {0:1}
At index j=0:
- prefixXOR[j] = 4
Do we have prefixXOR[j] ^ 0 == 0? No, but we check if prefixXOR[j] == prefixXOR[i-1].
Since there is no earlier prefixXOR equal to 4, the answer is 0.
But in cases where prefixXOR[j] itself is 0, we correctly find the subarray from 0 to j.
By initializing the count of prefixXOR = 0 as 1 in our map, we correctly count subarrays starting at index 0.
The final intuition:
We walk through the array, keep track of cumulative XOR as prefixXOR, and for each index j, find how many previous indices had the same prefixXOR → those correspond to beautiful subarrays ending at j.
We keep adding these counts to our answer, and finally return the total.
Approach
Step 1: Initialize Variables
We start by setting up the basic variables:
- n → stores the length of the input array nums.
- ans → initialized to 0, will store our final answer — the count of beautiful subarrays.
- currentXOR → initialized to 0, will track the cumulative XOR of elements from the start of the array up to the current index.
Step 2: Create PrefixXOR Map and Initialize
We create a prefixXOR map to record how many times each prefix XOR value has occurred so far.
We initialize prefixXOR[0] = 1.
This ensures that if the subarray starting from index 0 itself has a cumulative XOR of 0, we correctly count it as a beautiful subarray.
Step 3: Traverse the Array Element by Element
We now iterate through each element nums[i] in the array, from left to right (i = 0 to n − 1).
At each step, we update currentXOR to include the current number.
Step 4: Update the Current XOR
For the current number nums[i], update the running cumulative XOR:
currentXOR = currentXOR ^ nums[i]
This keeps track of the XOR of all elements from the start up to index i.
Step 5: Add Subarrays Ending Here That Have XOR Zero
If we have seen this currentXOR value before (i.e., prefixXOR[currentXOR] > 0), it means there exists at least one earlier index where the cumulative XOR up to that index was the same.
By the property of XOR:
- currentXOR ^ previous_currentXOR = 0 if currentXOR == previous_currentXOR
So, there are prefixXOR[currentXOR] subarrays ending at index i whose cumulative XOR is 0.
We add prefixXOR[currentXOR] to ans.
Step 6: Update the Count of the Current Prefix XOR
After processing index i, we record that we’ve now seen this currentXOR one more time:
prefixXOR[currentXOR]++
This ensures that future subarrays can correctly find and count matching prefixes that lead to XOR zero.
Step 7: Return the Final Result
After traversing the entire array, we return the value stored in ans.
This final number represents total count of beautiful subarrays.
Let us understand this with a video,
Dry Run
Let’s do a step-by-step dry run of the optimized prefix-XOR + prefix-counting approach for
nums = [4, 3, 1, 2, 4]
Step 1: Initialize all required variables
- n = 5 → length of input array
- ans = 0 → final count of beautiful subarrays
- currentXOR = 0 → tracks cumulative XOR from start to current index
Step 2: Create the prefixXOR map and initialize base case
- Create prefixXOR(hashmap): all counts initially 0
- Set prefixXOR[0] = 1
Step 3: Traverse the array element by element
Index = 0 → nums[0] = 4
Step 4: Update currentXOR
currentXOR = 0 ^ 4 = 4
Step 5: Add subarrays ending here with XOR zero
prefixXOR[4] = 0 → ans += 0 → ans = 0
Step 6: Update prefixXOR
prefixXOR[4] += 1 → prefixXOR[4] = 1
Index = 1 → nums[1] = 3
Step 4: Update currentXOR
currentXOR = 4 ^ 3 = 7
Step 5: Add subarrays ending here with XOR zero
prefixXOR[7] = 0 → ans += 0 → ans = 0
Step 6: Update prefixXOR
prefixXOR[7] += 1 → prefixXOR[7] = 1
Index = 2 → nums[2] = 1
Step 4: Update currentXOR
currentXOR = 7 ^ 1 = 6
Step 5: Add subarrays ending here with XOR zero
prefixXOR[6] = 0 → ans += 0 → ans = 0
Step 6: Update prefixXOR
prefixXOR[6] += 1 → prefixXOR[6] = 1
Index = 3 → nums[3] = 2
Step 4: Update currentXOR
currentXOR = 6 ^ 2 = 4
Step 5: Add subarrays ending here with XOR zero
prefixXOR[4] = 1 → ans += 1 → ans = 1
Step 6: Update prefixXOR
prefixXOR[4] += 1 → prefixXOR[4] = 2
Index = 4 → nums[4] = 4
Step 4: Update currentXOR
currentXOR = 4 ^ 4 = 0
Step 5: Add subarrays ending here with XOR zero
prefixXOR[0] = 1 → ans += 1 → ans = 2
Step 6: Update prefixXOR
prefixXOR[0] += 1 → prefixXOR[0] = 2
Step 7: Return the final result
Final value of ans = 2
The total number of beautiful subarrays in nums = [4, 3, 1, 2, 4] is 2.
Code for All Languages
C++
#include <iostream> // For input and output
#include <vector> // For using the vector data structure
#include <unordered_map> // For using hash map to store prefix XOR counts
using namespace std;
class Solution {
public:
long long beautifulSubarrays(vector<int>& nums) {
// Step 1: Initialize variable ans and currentXOR
long long ans = 0;
int currentXOR = 0;
int n = nums.size();
// Step 2: Create prefixXOR map and initialize base case
unordered_map<int, int> prefixXOR;
prefixXOR[0] = 1;
// Step 3: Traverse the array element by element
for (int idx = 0; idx < n; idx++) {
// Step 4: Update currentXOR
currentXOR ^= nums[idx];
// Step 5: Add subarrays ending here with XOR zero
ans += prefixXOR[currentXOR];
// Step 6: Update prefixXOR
prefixXOR[currentXOR]++;
}
// Step 7: Return the final answer
return ans;
}
};
int main() {
int n;
cin >> n;
vector<int> nums(n);
//take nums as input
for (int i = 0; i < n; i++) {
cin >> nums[i];
}
Solution sol;
long long result = sol.beautifulSubarrays(nums); // Call the function
cout << result << endl; // Output the result
return 0;
}
Java
import java.util.*; // For Scanner and HashMap
class Solution {
public long beautifulSubarrays(int[] nums) {
// Step 1: Initialize variable ans and currentXOR
long ans = 0;
int currentXOR = 0;
int n = nums.length;
// Step 2: Create prefixXOR map and initialize base case
Map<Integer, Integer> prefixXOR = new HashMap<>();
prefixXOR.put(0, 1);
// Step 3: Traverse the array element by element
for (int idx = 0; idx < n; idx++) {
// Step 4: Update currentXOR
currentXOR ^= nums[idx];
// Step 5: Add subarrays ending here with XOR zero
ans += prefixXOR.getOrDefault(currentXOR, 0);
// Step 6: Update prefixXOR
prefixXOR.put(currentXOR, prefixXOR.getOrDefault(currentXOR, 0) + 1);
}
// Step 7: Return the final answer
return ans;
}
}
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
int[] nums = new int[n];
//take nums as input
for (int i = 0; i < n; i++) {
nums[i] = sc.nextInt();
}
Solution sol = new Solution();
long result = sol.beautifulSubarrays(nums); // Call the function
System.out.println(result); // Output the result
}
}
Python
from typing import List # for input handling
class Solution:
def beautifulSubarrays(self, nums: List[int]) -> int:
# Step 1: Initialize variable ans and current_xor
ans = 0
current_xor = 0
n = len(nums)
# Step 2: Create prefixXOR dictionary and initialize base case
prefixXOR = {0: 1}
# Step 3: Traverse the array element by element
for idx in range(n):
# Step 4: Update current_xor
current_xor ^= nums[idx]
# Step 5: Add subarrays ending here with XOR zero
ans += prefixXOR.get(current_xor, 0)
# Step 6: Update prefixXOR
prefixXOR[current_xor] = prefixXOR.get(current_xor, 0) + 1
# Step 7: Return the final answer
return ans
if __name__ == "__main__":
n = int(input())
nums = list(map(int, input().split())) # Input the list
sol = Solution()
result = sol.beautifulSubarrays(nums) # Call the function
print(result) # Print the result
Javascript
/**
* @param {number[]} nums - The input array of integers
* @return {number} - Total number of beautiful subarrays
*/
var beautifulSubarrays = function(nums) {
// Step 1: Initialize variable ans and currentXor
let ans = 0;
let currentXor = 0;
const n = nums.length;
// Step 2: Create prefixXOR map and initialize base case
const prefixXOR = new Map();
prefixXOR.set(0, 1);
// Step 3: Traverse the array element by element
for (let idx = 0; idx < n; idx++) {
// Step 4: Update currentXor
currentXor ^= nums[idx];
// Step 5: Add subarrays ending here with XOR zero
ans += prefixXOR.get(currentXor) || 0;
// Step 6: Update prefixXOR
prefixXOR.set(currentXor, (prefixXOR.get(currentXor) || 0) + 1);
}
// Step 7: Return the final answer
return ans;
};
// Driver code
const readline = require("readline");
const rl = readline.createInterface({
input: process.stdin,
output: process.stdout
});
let inputs = [];
rl.on("line", function(line) {
inputs.push(line.trim());
if (inputs.length === 2) {
const nums = inputs[1].split(' ').map(Number);
const result = beautifulSubarrays(nums);
console.log(result);
rl.close();
}
});
Time Complexity: O(n)
Outer Loop / Traversal: O(n)
We traverse the array once from index 0 to n - 1.
Let’s denote:
- n = length of the input array nums
This traversal itself runs in O(n) time.
Prefix XOR Update: O(1)
At each index idx, we compute:
- currentXOR ^= nums[idx]
This is a single XOR operation, which takes O(1) time.
prefixXOR Lookup & Update: O(1)
For each index:
- Lookup: prefixXOR.get(currentXOR, 0) → O(1)
- Update: prefixXOR[currentXOR] += 1 → O(1)
Hash map operations (get/set) have average-case complexity of O(1).
Total Time per Iteration: O(1)
Each iteration over one element involves:
- Updating the XOR → O(1)
- Checking prefixXOR → O(1)
- Updating prefixXOR → O(1)
So the total work per element is constant.
Since we only make a single traversal of length n, and each operation inside the loop is O(1),
the overall time complexity is: O(n)
Space Complexity: O(n)
Auxiliary Space Complexity: O(n)
This is the extra space used by the algorithm, excluding the input and output.
In this optimized prefix XOR approach, we use:
- A hash map prefixXOR to store the counts of prefix XOR values seen so far.
Since:
- currentXOR can have up to O(n) unique values (in the worst case, every prefix XOR is unique),
- The size of prefixXOR can be up to O(n).
We also store:
- The variable currentXOR → single integer → O(1)
- The variable ans→ single integer → O(1)
So, the dominant part is the hash map, giving auxiliary space complexity = O(n).
- Input space:
- The input array nums of length n → O(n)
- Output space:
- Just a single integer answer → O(1)
- Auxiliary space:
- Hash map prefixXOR→ up to O(n)
So, the total space complexity becomes:
O(n) + O(1) + O(n) = O(n)
Learning Tip
Now we have successfully tackled this problem, let's try these similar problems.
You are given a sorted array nums of n non-negative integers and an integer maximumBit. You want to perform the following query n times:
Find a non-negative integer k < 2^maximumBit such that nums[0] XOR nums[1] XOR ... XOR nums[nums.length-1] XOR k is maximized.
k is the answer to the ith query.
Remove the last element from the current array nums.
Return an array answer, where answer[i] is the answer to the ith query.
You are given two integers n and maxValue, which are used to describe an ideal array.
A 0-indexed integer array arr of length n is considered ideal if the following conditions hold:
Every arr[i] is a value from 1 to maxValue, for 0 <= i < n.
Every arr[i] is divisible by arr[i - 1], for 0 < i < n.
Return the number of distinct ideal arrays of length n. Since the answer may be very large, return it modulo 10^9 + 7.