Skip to main content

Matrix

Count Submatrices with Top-Left Element and Sum Less Than k Solution In C++/Python/java/JS

Problem Description:

You are given a 0-indexed integer matrix grid and an integer k.
Return the number of submatrices that contain the top-left element of the grid, and have a sum less than or equal to k.
Illustration of Count Submatrices with Top-Left Element and Sum Less Than k - Problem Description

Examples:

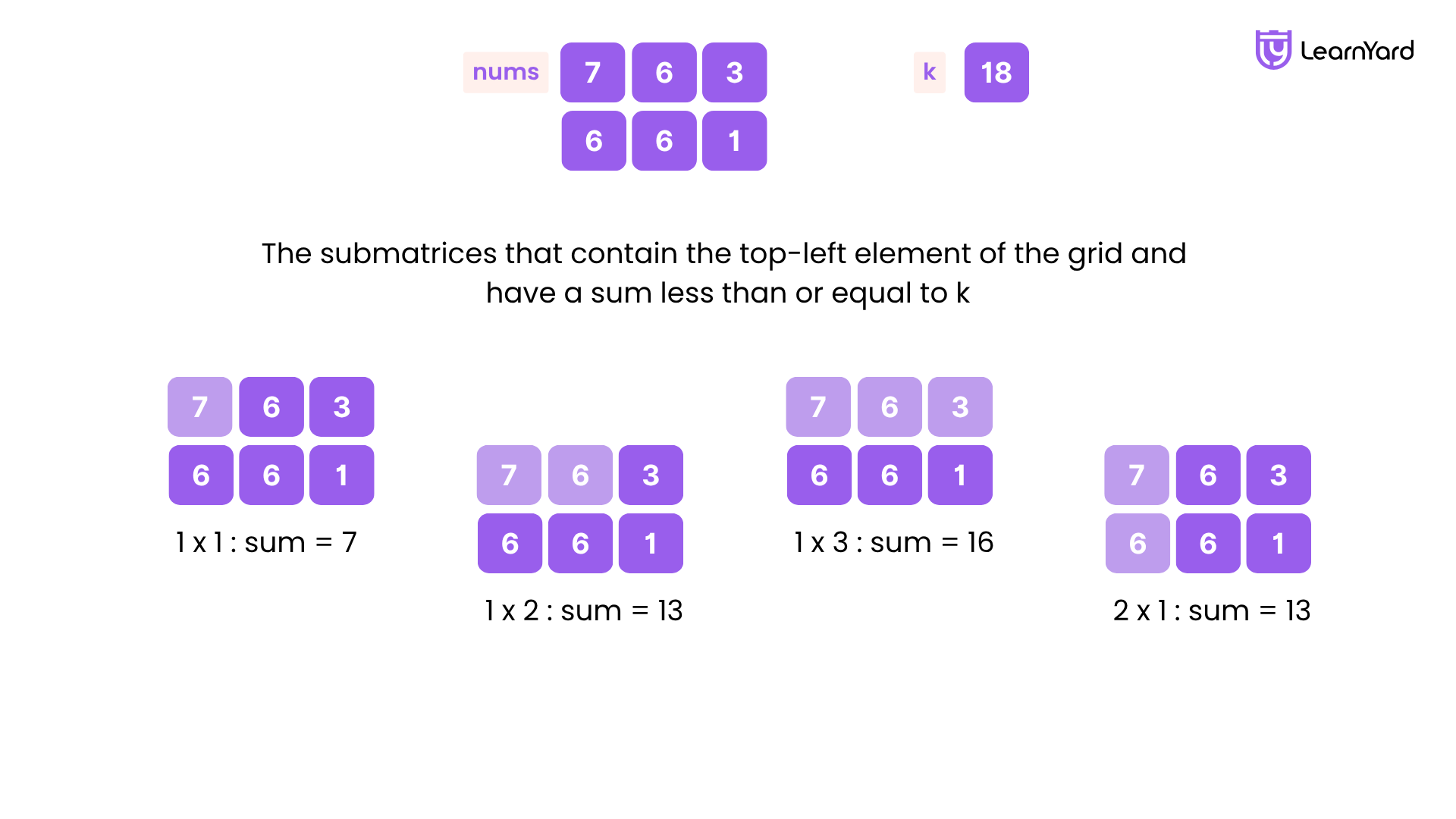
Illustration of Count Submatrices with Top-Left Element and Sum Less Than k - Example 1

Input: grid = [[7,6,3],[6,6,1]], k = 18
Output: 4
Explanation: There are only 4 submatrices, shown in the image above, that contain the top-left element of grid, and have a sum less than or equal to 18.

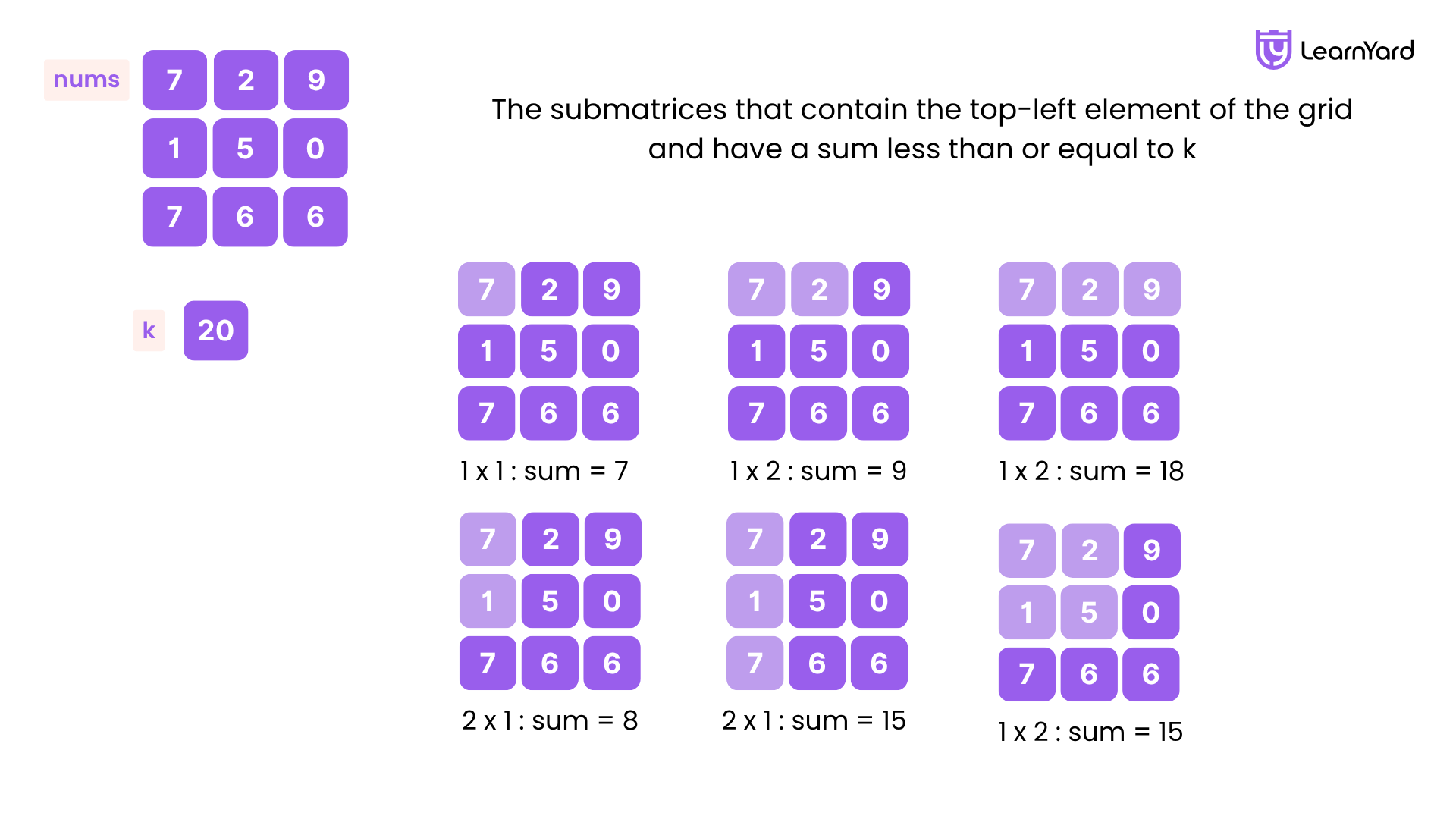
Illustration of Count Submatrices with Top-Left Element and Sum Less Than k - Example 2

Input: grid = [[7,2,9],[1,5,0],[2,6,6]], k = 20
Output: 6
Explanation: There are only 6 submatrices, shown in the image above, that contain the top-left element of grid, and have a sum less than or equal to 20.

Constraints:

  • m == grid.length
  • n == grid[i].length
  • 1 <= n, m <= 1000
  • 0 <= grid[i][j] <= 1000
  • 1 <= k <= 109
We need to count how many submatrices include the top-left element (the cell at index [0][0]) and have a sum less than or equal to k.
This means we’re only focusing on submatrices that start from the top-left corner, and we want to check if the sum of all elements inside each is at most k.
Naturally, the first approach would be to go through every possible submatrix that starts from the top-left and calculate its sum one by one.
Let’s explore this basic approach in more detail...

Brute Force Approach

Intuition

We need to go through each submatrix starting from the top-left corner and include it in our answer only if its sum is less than or equal to k.

What is a Submatrix?

Before we understand a submatrix, let's quickly recall what a matrix is.

A matrix is a rectangular grid of numbers arranged in rows and columns. For example, this is a 3x3 matrix (3 rows and 3 columns):

1 2 3
4 5 6
7 8 9

A submatrix is a smaller rectangular portion of a matrix. It is formed by selecting some continuous rows and columns from the original matrix.

  • The key point is that the rows and columns must be contiguous (i.e., side by side, with no gaps).
  • The shape of a submatrix is always rectangular, even if it's just a single element.

Examples:

Let’s take the same 3x3 matrix again:

1 2 3
4 5 6
7 8 9

From this matrix, we can extract many submatrices:

  • 1x1 Submatrix (just a single element):

5
This is a submatrix starting at row 2, column 2 (0-based index).

  • 2x2 Submatrix:

2 3
5 6
This submatrix starts at index 0, 1 and ends at index 1, 2.

  • 3x1 Submatrix (a column):

3
6
9

  • 1x3 Submatrix (a row):

4 5 6

  • Entire matrix (3x3):

1 2 3
4 5 6
7 8 9

All of these are valid submatrices because:

  • They are rectangular.
  • They contain only elements that are next to each other in both row and column directions.

How Many Submatrices Are There?

In an n x m matrix (n rows and m columns), the number of possible submatrices is:

(n × (n+1) / 2) × (m × (m+1) 2)

This is because you can choose a range of rows in n(n+1)/2 ways, and a range of columns in m(m+1)/2 ways. Each combination gives a unique submatrix.

Summary

  • A submatrix is a rectangular section of a matrix.
  • It is defined by choosing a starting row and column, and an ending row and column.
  • Rows and columns in the submatrix must be contiguous.
  • Submatrices can be as small as one element or as large as the entire matrix.

To solve this problem, we will go through each index in the matrix and treat it as the bottom-right corner (also called the ending index) of a submatrix. Let's call this index (er, ec), where er is the ending row, and ec is the ending column.

Since we are only interested in submatrices that start at the top-left corner, the submatrix we are checking will always start at (0, 0) and end at (er, ec).

Once we fix a submatrix from (0, 0) to (er, ec), we can:

  • Loop through every element inside this submatrix,
  • Add the elements one by one to a variable called sum.

After calculating the sum of the submatrix:

  • If the sum is less than or equal to k, we increment our answer count by 1.

We can use a variable, ans, to keep track of how many such submatrices satisfy this condition.

Count Submatrices with Top-Left Element and Sum Less Than k Algorithm

Step 1: Determine the Size of the Matrix

Begin by finding how many rows and columns are in the given matrix.
This helps you know how far you can iterate when checking submatrices.

Step 2: Initialise the Counter

Create a variable, say cnt, and set it to 0.
This will be used to count the number of valid submatrices whose sum is less than or equal to k.

Step 3: Choose Bottom-Right Corners of Submatrices

Loop through each cell (er, ec) of the matrix.
Consider each of these cells as the bottom-right corner of a submatrix that starts from the top-left corner (0, 0).

Step 4: Calculate the Sum of the Submatrix

For every (er, ec), use two more loops to iterate from row 0 to er and column 0 to ec.
Inside these loops, add each value to a sum variable to calculate the total sum of elements in the submatrix from (0, 0) to (er, ec).

Step 5: Check if the Sum is Valid

After computing the sum, compare it with k.
If the sum is less than or equal to k, it means this submatrix is valid, so you increment the counter cnt by 1.

Step 6: Repeat for All Possible Submatrices

Repeat this process for all combinations of (er, ec) in the matrix.
By the end, every possible submatrix starting at (0, 0) will have been checked.

Step 7: Return the Final Answer

Finally, return the value stored in cnt.
This gives the total number of submatrices starting at (0, 0) that have a sum less than or equal to k.

Illustration of Count Submatrices with Top-Left Element and Sum Less Than k - Brute Force 1
Illustration of Count Submatrices with Top-Left Element and Sum Less Than k - Brute Force 2
Illustration of Count Submatrices with Top-Left Element and Sum Less Than k - Brute Force 3

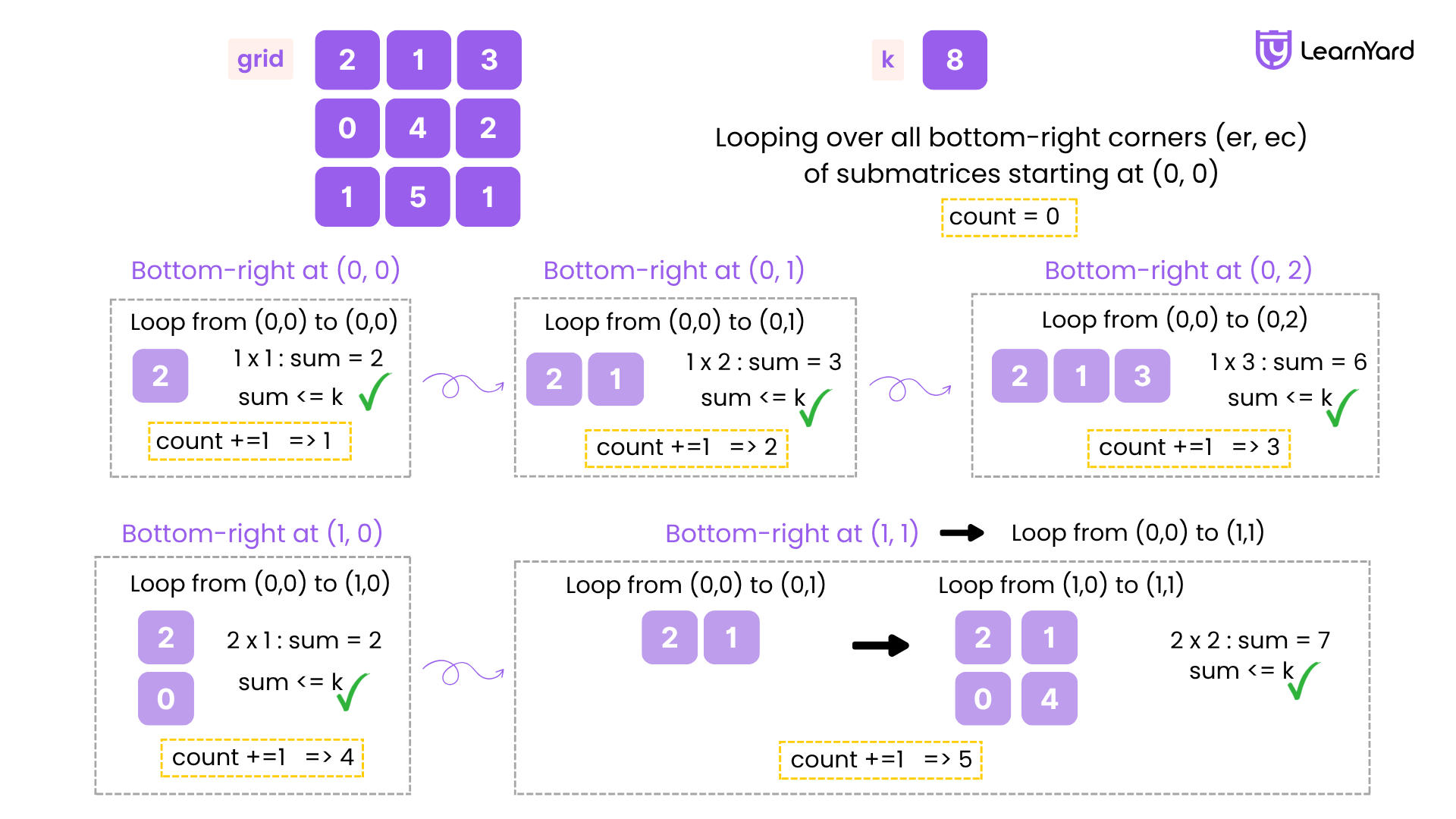
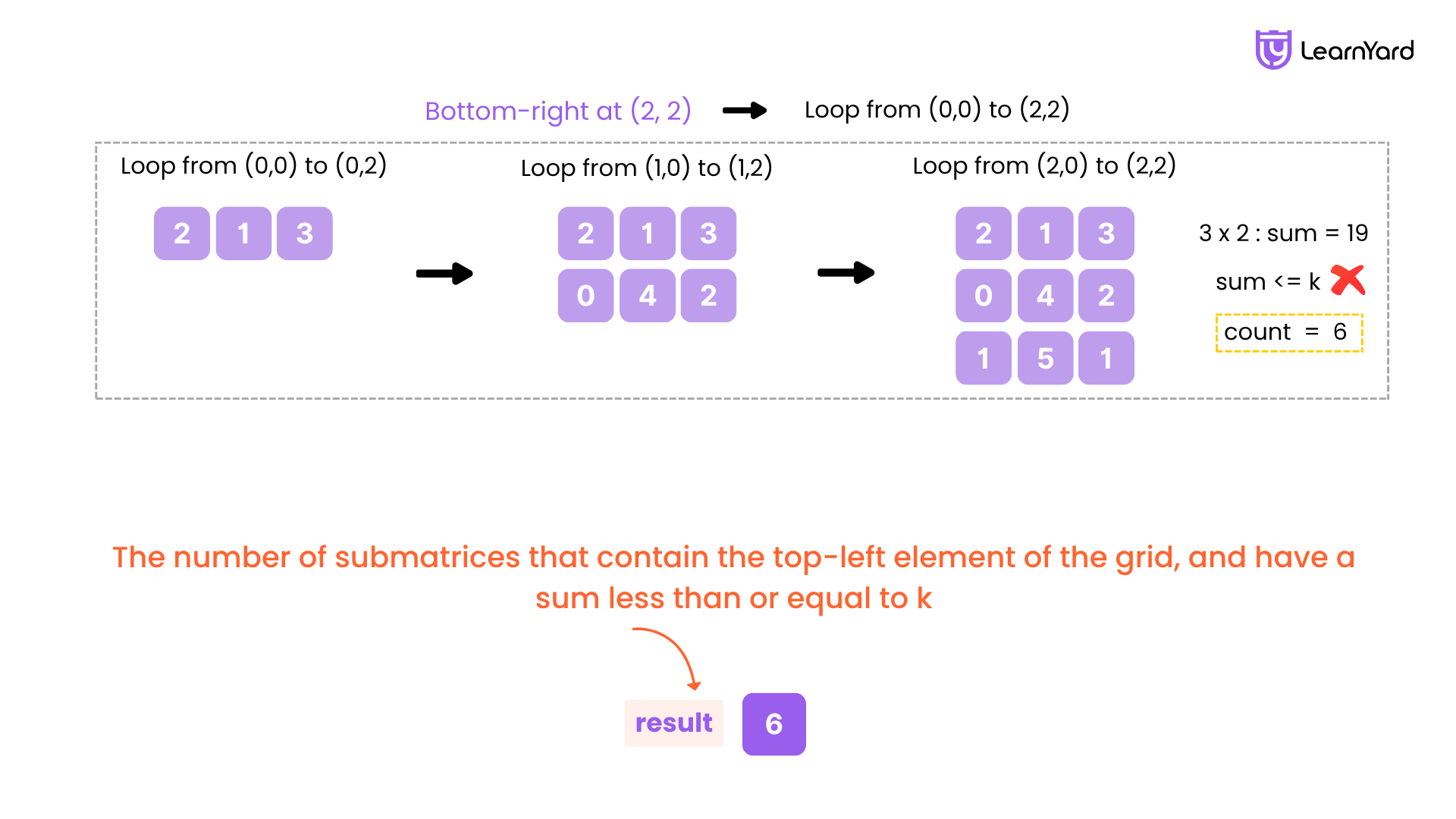
Count Submatrices with Top-Left Element and Sum Less Than k Example

Input: grid = [[1,2,3],[4,5,6]], k = 12
Output: 5
Explanation: There are only 5 submatrices that contain the top-left element of the grid, and have a sum less than or equal to 12.

We loop over all bottom-right corners (er, ec) of submatrices starting at (0, 0), and for each, we calculate the sum from (0,0) to (er,ec) by visiting every cell in that region.

Bottom-right at (0, 0)
Loop from (0,0) to (0,0):

  • sum = 0
  • Add grid[0][0] = 1 → sum = 1
    → 1 ≤ 12 → Count = 1

Bottom-right at (0, 1)
Loop from (0,0) to (0,1):

  • sum = 0
  • Add grid[0][0] = 1 → sum = 1
  • Add grid[0][1] = 2 → sum = 3
    → 3 ≤ 12 → Count = 2

Bottom-right at (0, 2)
Loop from (0,0) to (0,2):

  • sum = 0
  • Add grid[0][0] = 1 → sum = 1
  • Add grid[0][1] = 2 → sum = 3
  • Add grid[0][2] = 3 → sum = 6
    → 6 ≤ 12 → Count = 3

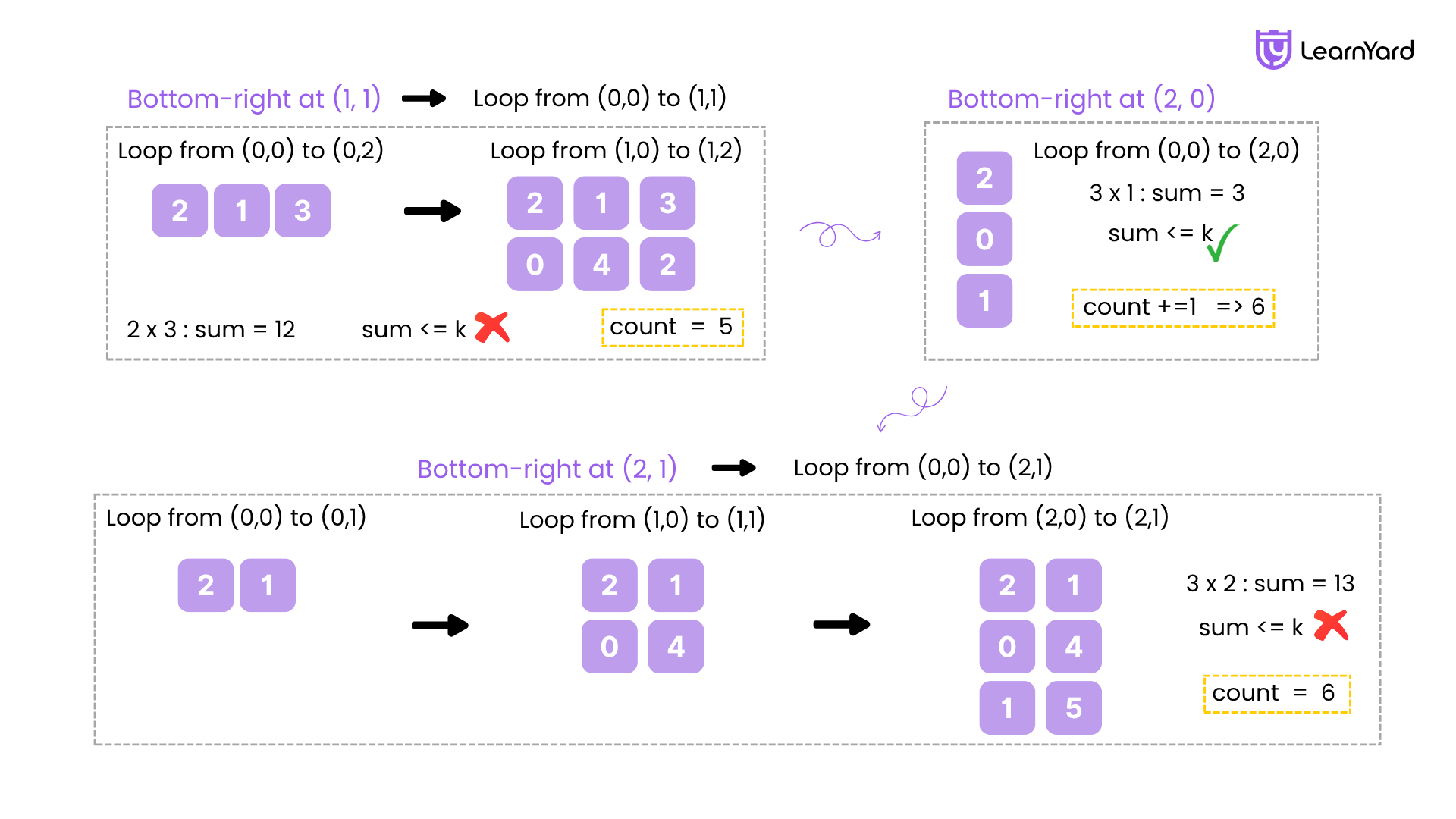
Bottom-right at (1, 0)
Loop from (0,0) to (1,0):

  • sum = 0
  • Add grid[0][0] = 1 → sum = 1
  • Add grid[1][0] = 4 → sum = 5
    → 5 ≤ 12 → Count = 4

Bottom-right at (1, 1)
Loop from (0,0) to (1,1):

  • sum = 0
  • Add grid[0][0] = 1 → sum = 1
  • Add grid[0][1] = 2 → sum = 3
  • Add grid[1][0] = 4 → sum = 7
  • Add grid[1][1] = 5 → sum = 12
    → 12 ≤ 12 → Count = 5

Bottom-right at (1, 2)
Loop from (0,0) to (1,2):

  • sum = 0
  • Add grid[0][0] = 1 → sum = 1
  • Add grid[0][1] = 2 → sum = 3
  • Add grid[0][2] = 3 → sum = 6
  • Add grid[1][0] = 4 → sum = 10
  • Add grid[1][1] = 5 → sum = 15
  • Add grid[1][2] = 6 → sum = 21
    → 21 > 12 → Count remains 5

Final Count = 5

Count Submatrices with Top-Left Element and Sum Less Than k Solution
Count Submatrices with Top-Left Element and Sum Less Than k solution in C++ 
class Solution {
public:
    int countSubmatrices(vector<vector<int>>& grid, int k) {
        // Get number of rows
        int n = grid.size();
        // Get number of columns
        int m = grid[0].size();
        // Initialize count of submatrices
        int cnt = 0;

        // Loop for all possible bottom-right corners of submatrices
        for (int er = 0; er < n; ++er) {
            for (int ec = 0; ec < m; ++ec) {
                // Sum of current submatrix from (0,0) to (er, ec)
                int sum = 0;
                // Loop through all cells inside submatrix
                for (int i = 0; i <= er; ++i) {
                    for (int j = 0; j <= ec; ++j) {
                        sum += grid[i][j];
                    }
                }
                // If sum is less than or equal to k, increment the count
                if (sum <= k)
                    cnt++;
            }
        }
        // Return the total count
        return cnt;
    }
};

Count Submatrices with Top-Left Element and Sum Less Than k solution in Java 
class Solution {
    public int countSubmatrices(int[][] grid, int k) {
        // Number of rows
        int n = grid.length;
        // Number of columns
        int m = grid[0].length;
        // Initialize the counter
        int cnt = 0;

        // Iterate through all possible bottom-right corners
        for (int er = 0; er < n; ++er) {
            for (int ec = 0; ec < m; ++ec) {
                // Sum of current submatrix from (0,0) to (er,ec)
                int sum = 0;
                // Sum up elements in the submatrix
                for (int i = 0; i <= er; ++i) {
                    for (int j = 0; j <= ec; ++j) {
                        sum += grid[i][j];
                    }
                }
                // If sum is less than or equal to k, increment the count
                if (sum <= k)
                    cnt++;
            }
        }
        // Return the total count
        return cnt;
    }
}

Count Submatrices with Top-Left Element and Sum Less Than k solution in Python 
class Solution:
    def countSubmatrices(self, grid: List[List[int]], k: int) -> int:
        # Get number of rows
        n = len(grid)
        # Get number of columns
        m = len(grid[0])
        # Initialize the counter
        cnt = 0

        # Iterate through all possible bottom-right corners
        for er in range(n):
            for ec in range(m):
                # Sum for current submatrix (from [0,0] to [er,ec])
                sum_ = 0
                # Sum up all values within top-left (0,0) to (er,ec)
                for i in range(er + 1):
                    for j in range(ec + 1):
                        sum_ += grid[i][j]
                # If sum is less than or equal to k, increment the counter
                if sum_ <= k:
                    cnt += 1
        # Return the total count
        return cnt

Count Submatrices with Top-Left Element and Sum Less Than k solution in Javascript 
/**
 * @param {number[][]} grid
 * @param {number} k
 * @return {number}
 */
var countSubmatrices = function(grid, k) {
    // Get the number of rows
    const n = grid.length;
    // Get the number of columns
    const m = grid[0].length;
    // Counter for valid submatrices
    let cnt = 0;

    // Loop through all possible bottom-right corners
    for (let er = 0; er < n; ++er) {
        for (let ec = 0; ec < m; ++ec) {
            // Sum of submatrix (from [0,0] to [er,ec])
            let sum = 0;
            // Calculate the sum for this top-left to current corner
            for (let i = 0; i <= er; ++i) {
                for (let j = 0; j <= ec; ++j) {
                    sum += grid[i][j];
                }
            }
            // If sum is less than or equal to k, increment counter
            if (sum <= k) cnt++;
        }
    }
    // Return the total count
    return cnt;
};

Count Submatrices with Top-Left Element and Sum Less Than k Complexity Analysis

Time Complexity: O(n2 × m2)

Outer Two Loops : Choosing Submatrices

The outer part of the algorithm runs two nested loops:

  • The first loop runs from er = 0 to n - 1 (for rows).
  • The second loop runs from ec = 0 to m - 1 (for columns).

These two loops are used to select every possible bottom-right corner of a submatrix that starts from the fixed top-left corner (0, 0).

  • Number of iterations = n × m
    So just this part contributes O(n × m).

Inner Two Loops : Calculating Sum for Each Submatrix

For each (er, ec) position chosen, you want to calculate the sum of all values in the submatrix that starts at (0, 0) and ends at (er, ec).

This again requires two more nested loops:

  • Loop from i = 0 to er (i.e., up to n)
  • Loop from j = 0 to ec (i.e., up to m)

So, for each such (er, ec), you may end up looping through roughly er × ec elements to compute the sum.

In the worst case, when (er, ec) = (n-1, m-1), the entire grid is traversed to compute the sum, which takes O(n × m) time.

Putting It All Together

You are doing the sum calculation (inner loops) for each possible (er, ec) (outer loops). So you are essentially doing:

  • O(n × m) outer iterations, and
  • For each, a sum computation in up to O(n × m) time.

Thus, the overall time complexity is:

O(n × m) × O(n × m) = O(n² × m²)

Space Complexity : O(1)

Auxiliary Space Complexity

This refers to the extra space used, excluding input and output.
In the given approach, we are only using a few integer variables:

  • n, m for dimensions
  • cnt for counting submatrices
  • sum for holding submatrix sum
  • Loop variables (i, j, er, ec)

All of these are simple integers; they take constant space.
Auxiliary Space Complexity: O(1)

Total Space Complexity

This includes input + output + auxiliary space.

  • Input is the grid, which is a 2D vector of size n × m
  • Output is an integer (the count), which is negligible
  • Auxiliary space is O(1) as shown above

Total Space Complexity: O(n × m)
(due to the input grid)

Is the Brute Force Approach Efficient?

The brute force approach is inefficient because it calculates the sum of each possible submatrix starting from the top-left corner (0, 0) to every possible bottom-right corner (i, j) by iterating over all its cells individually. For a matrix of size n × m, this results in O(n² × m²) time complexity.

Now, since both n and m can go up to 1000, the total number of operations in the worst case becomes:

1,000² × 1,000² = 10¹² operations

This scale of computation is too large to execute within the time limits of most programming environments. Standard time constraints (typically 1 to 2 seconds) can handle up to around 10⁸ operations efficiently, so this brute force method would be far too slow and would likely time out or hang, especially with larger inputs. That's why it’s considered inefficient and not suitable for production or competitive programming under these constraints.

In the brute force approach, the first two nested loops are used to traverse every index of the matrix, allowing us to treat each one as the bottom-right corner (ending point) of a potential submatrix that starts from the top-left corner.
The remaining two nested loops then go back and revisit all the cells within that submatrix to calculate its total sum. This repeated scanning of the same areas makes the algorithm slow and inefficient.
Now the question is: Can we do better?
Can we avoid these two inner loops used for calculating the sum?
In other words, is there a way to compute the sum of any submatrix efficiently without revisiting all of its elements each time?

Optimal Approach

Intuition

If we can somehow calculate the sum of elements inside any submatrix in O(1) time, our solution would become much more efficient. We could simply check if that sum is less than or equal to k, and if it is, increment our count using the ans variable.

To achieve this constant-time sum calculation, we can use the concept of prefix sum in a matrix.

This technique allows us to precompute the sums of rectangular regions in advance, so that later, we can retrieve the sum of any submatrix in O(1).

The concept of prefix sum in a matrix.

We want a way to precompute the sum of every submatrix starting from (0, 0) to (er, ec) in advance, so later we can just look up the sum in constant time.

This is where the prefix sum in a matrix helps us.

Let’s take an example matrix:

matrix = [
[1, 2, 3],
[4, 5, 6],
[7, 8, 9]
]

We’ll create a prefix sum matrix of the same size.

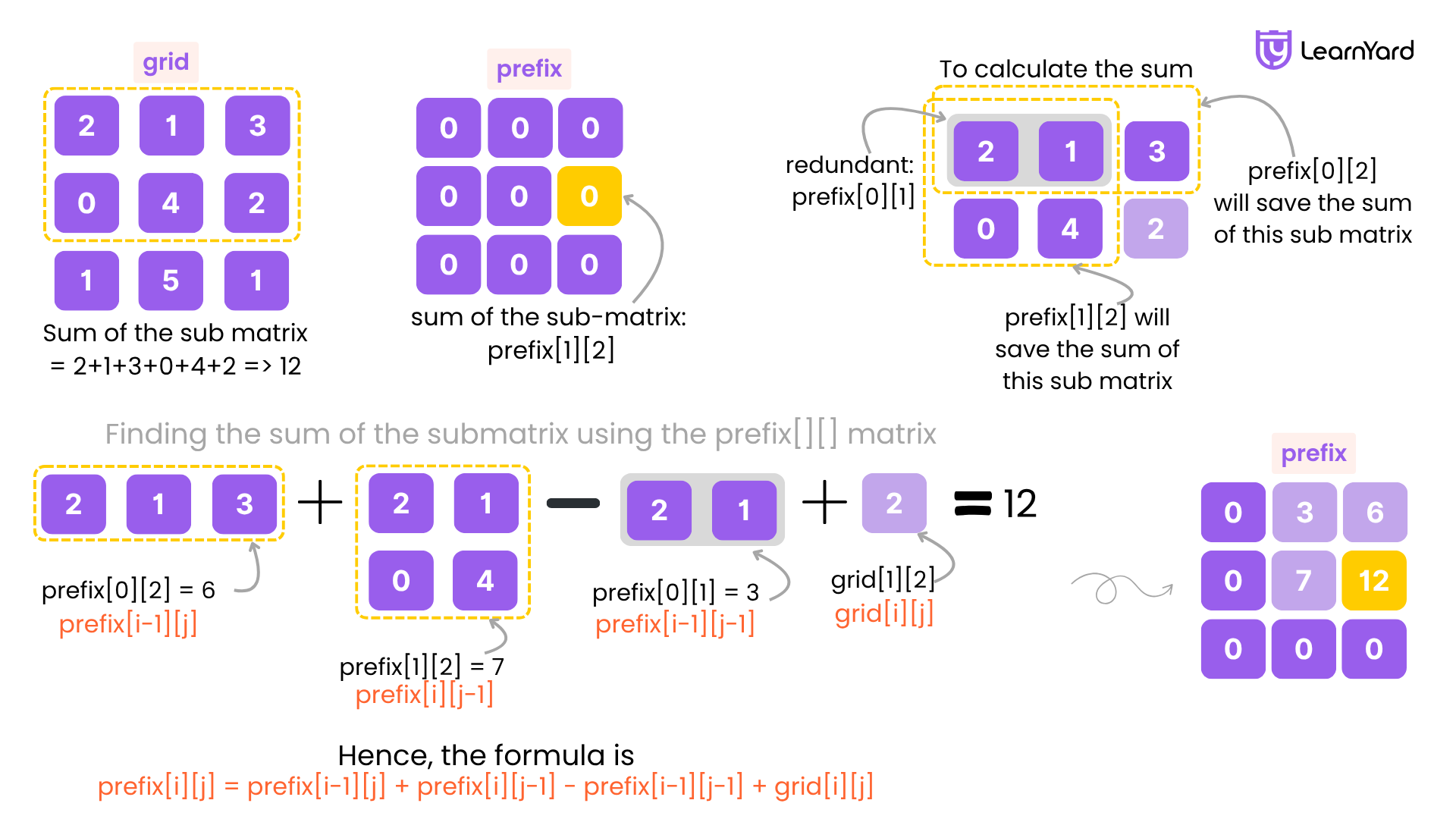
Let’s define prefix[i][j] as the sum of all elements from (0, 0) to (i, j) i.e., the top-left rectangle ending at (i, j).

Let’s walk through how to compute prefix[i][j] step by step.

What’s the Idea?

To get the sum from (0,0) to (i,j), we combine three things:

  1. The sum of the row above: prefix[i-1][j]
  2. The sum of the column to the left: prefix[i][j-1]
  3. Subtract the overlap (top-left block that got added twice): prefix[i-1][j-1]
  4. Finally, add the current cell matrix[i][j]

So, the formula becomes:

prefix[i][j] = prefix[i-1][j] + prefix[i][j-1] - prefix[i-1][j-1] +matrix[i][j]

This formula avoids counting the top-left overlap block twice.

Let’s Apply It to Our Examples

Step 1: Initialize prefix[0][0] = matrix[0][0] = 1

Now fill the rest of row 0:
prefix[0][1] = prefix[0][0] + matrix[0][1] = 1 + 2 = 3
prefix[0][2] = prefix[0][1] + matrix[0][2] = 3 + 3 = 6

Now fill the rest of column 0:
prefix[1][0] = prefix[0][0] + matrix[1][0] = 1 + 4 = 5
prefix[2][0] = prefix[1][0] + matrix[2][0] = 5 + 7 = 12

Now fill the rest using the formula:
prefix[1][1] = prefix[0][1] + prefix[1][0] - prefix[0][0] + matrix[1][1]
= 3 + 5 - 1 + 5 = 12

prefix[1][2] = prefix[0][2] + prefix[1][1] - prefix[0][1] + matrix[1][2]
= 6 + 12 - 3 + 6 = 21

And so on...

Eventually, your prefix matrix becomes:

[
[1, 3, 6],
[5, 12, 21],
[12, 27, 45]
]

So now, prefix[2][2] = 45 means the sum of all elements from (0,0) to (2,2) is 45, and we get that in O(1) time.

Illustration of Count Submatrices with Top-Left Element and Sum Less Than k - Prefix Sum Formula.

Now that we understand how prefix sums work in a matrix, our next step is to build a new matrix called the prefix sum matrix that has the same number of rows and columns as the original matrix. We’ll fill this matrix using the formula we discussed earlier.

Once this prefix matrix is ready, we can directly use prefix[i][j] to get the sum of all elements in the submatrix starting from the top-left corner (0, 0) to the position (i, j) in O(1) time.

Everything else in our approach stays the same; this optimisation helps us avoid recalculating the sum again and again.

Count Submatrices with Top-Left Element and Sum Less Than k Algorithm

Step 1: Get the Dimensions of the Matrix

First, extract the number of rows and columns from the given grid matrix.
You’ll need this information to create a new matrix of the same size and to run nested loops over the grid.

Step 2: Create a Prefix Sum Matrix

Now, create a new 2D vector prefix of the same dimensions as the input grid.
Initialise all cells in this matrix to 0. This new matrix will be used to store the cumulative sum from (0,0) to every cell (i,j).

Step 3: Fill the Prefix Sum Matrix

Iterate over every cell (i,j) of the original grid and update the corresponding prefix[i][j] using the following logic:

  • Start with prefix[i][j] = grid[i][j]
  • If a cell exists above (i.e., i > 0), add prefix[i-1][j]
  • If a cell exists to the left (i.e., j > 0), add prefix[i][j-1]
  • If a top-left diagonal cell exists (i.e., i > 0 && j > 0), subtract prefix[i-1][j-1] to remove the overlapping sum (which got added twice)

By doing this, prefix[i][j] will now contain the sum of the submatrix from (0,0) to (i,j).

Step 4: Count Submatrices with Sum ≤ k

Now that your prefix matrix is ready, iterate again over all cells of the matrix.
Each cell (er, ec) in the prefix matrix represents the sum of the submatrix from the top-left corner (0,0) to (er,ec).

If this sum is less than or equal to k, increment your count.

Step 5: Return the Count

Finally, return the total count of such submatrices found in step 4.

0:00
/3:12

Animation of Count Submatrices with Top-Left Element and Sum Less Than k - Optimal Approach

Count Submatrices with Top-Left Element and Sum Less Than k Example

Build Prefix Sum Matrix

We'll fill the prefix matrix prefix[i][j] such that it represents the sum of all elements from (0,0) to (i,j).

Let’s go cell by cell:

Cell (0,0):

  • prefix[0][0] = grid[0][0] = 1

Cell (0,1):

  • prefix[0][1] = prefix[0][0] + grid[0][1] = 1 + 2 = 3

Cell (0,2):

  • prefix[0][2] = prefix[0][1] + grid[0][2] = 3 + 3 = 6

Cell (1,0):

  • prefix[1][0] = prefix[0][0] + grid[1][0] = 1 + 4 = 5

Cell (1,1):

  • prefix[1][1] = prefix[0][1] + prefix[1][0] - prefix[0][0] + grid[1][1] = 3 + 5 - 1 + 5 = 12

Cell (1,2):

  • prefix[1][2] = prefix[0][2] + prefix[1][1] - prefix[0][1] + grid[1][2] = 6 + 12 - 3 + 6 = 21

Final Prefix Matrix:
[
[1, 3, 6],
[5, 12, 21]
]

Each cell (i, j) here gives the sum of the submatrix (0, 0) to (i, j).

Count Valid Submatrices

Now loop over each cell (er, ec):

  • (0,0) → prefix = 1 → <= k → Yes → count = 1
  • (0,1) → prefix = 3 → <= k → Yes → count = 2
  • (0,2) → prefix = 6 → <= k → Yes → count = 3
  • (1,0) → prefix = 5 → <= k → Yes → count = 4
  • (1,1) → prefix = 12 → <= k → Yes → count = 5
  • (1,2) → prefix = 21 → <= k → No → count stays 5

Final Answer: 5

Count Submatrices with Top-Left Element and Sum Less Than k leetcode Solution
Count Submatrices with Top-Left Element and Sum Less Than k solution in C++ 
class Solution {
public:
    int countSubmatrices(vector<vector<int>>& grid, int k) {
        // Get number of rows and columns
        int n = grid.size();
        int m = grid[0].size();

        // Initialize prefix sum 2D vector with zeros
        vector<vector<int>> prefix(n, vector<int>(m, 0));

        // Build prefix sum matrix
        for (int i = 0; i < n; ++i) {
            for (int j = 0; j < m; ++j) {
                // Add value from cell above if present
                if (i > 0) prefix[i][j] += prefix[i-1][j];
                // Add value from cell to the left if present
                if (j > 0) prefix[i][j] += prefix[i][j-1];
                // Remove the overlap (cell at top-left diagonal) if present
                if (i > 0 && j > 0) prefix[i][j] -= prefix[i-1][j-1];
                // Add the actual grid value to this prefix cell
                prefix[i][j] += grid[i][j];
            }
        }

        // Initialize counter for valid submatrices
        int cnt = 0;
        // Count prefix sums that are <= k (all submatrices starting at (0,0))
        for (int er = 0; er < n; ++er) {
            for (int ec = 0; ec < m; ++ec) {
                if (prefix[er][ec] <= k) cnt++;
            }
        }

        // Return the count
        return cnt;
    }
};

Count Submatrices with Top-Left Element and Sum Less Than k solution in Java 
class Solution {
    public int countSubmatrices(int[][] grid, int k) {
        // Number of rows and columns
        int n = grid.length;
        int m = grid[0].length;

        // Create prefix sum matrix with zeros
        int[][] prefix = new int[n][m];

        // Build prefix sum matrix
        for (int i = 0; i < n; ++i) {
            for (int j = 0; j < m; ++j) {
                if (i > 0) prefix[i][j] += prefix[i-1][j];           // Add above
                if (j > 0) prefix[i][j] += prefix[i][j-1];           // Add left
                if (i > 0 && j > 0) prefix[i][j] -= prefix[i-1][j-1];// Remove overlap
                prefix[i][j] += grid[i][j];                          // Add current grid value
            }
        }

        // Count valid submatrices (prefix sums <= k)
        int cnt = 0;
        for (int er = 0; er < n; ++er) {
            for (int ec = 0; ec < m; ++ec) {
                if (prefix[er][ec] <= k) cnt++;
            }
        }
        return cnt;
    }
}

Count Submatrices with Top-Left Element and Sum Less Than k solution in Python 
class Solution:
    def countSubmatrices(self, grid: List[List[int]], k: int) -> int:
        # Number of rows and columns
        n = len(grid)
        m = len(grid[0])

        # Create prefix sum grid
        prefix = [[0] * m for _ in range(n)]

        # Build prefix sum matrix
        for i in range(n):
            for j in range(m):
                # Start with 0
                prefix[i][j] = 0
                # Add above
                if i > 0:
                    prefix[i][j] += prefix[i-1][j]
                # Add left
                if j > 0:
                    prefix[i][j] += prefix[i][j-1]
                # Subtract overlap
                if i > 0 and j > 0:
                    prefix[i][j] -= prefix[i-1][j-1]
                # Add grid value
                prefix[i][j] += grid[i][j]

        # Initialize answer
        cnt = 0
        # Count submatrices where prefix sum is <= k
        for er in range(n):
            for ec in range(m):
                if prefix[er][ec] <= k:
                    cnt += 1
        # Return the answer
        return cnt

Count Submatrices with Top-Left Element and Sum Less Than k solution in Javascript 
/**
 * @param {number[][]} grid
 * @param {number} k
 * @return {number}
 */
var countSubmatrices = function(grid, k) {
    // Get number of rows and columns
    const n = grid.length;
    const m = grid[0].length;

    // Create prefix sum matrix initialized to zero
    const prefix = Array.from({length: n}, () => Array(m).fill(0));

    // Build prefix sum matrix
    for (let i = 0; i < n; ++i) {
        for (let j = 0; j < m; ++j) {
            // Add above if valid
            if (i > 0) prefix[i][j] += prefix[i-1][j];
            // Add left if valid
            if (j > 0) prefix[i][j] += prefix[i][j-1];
            // Subtract overlap if valid
            if (i > 0 && j > 0) prefix[i][j] -= prefix[i-1][j-1];
            // Add the grid value
            prefix[i][j] += grid[i][j];
        }
    }

    // Count valid submatrices (prefix <= k)
    let cnt = 0;
    for (let er = 0; er < n; ++er) {
        for (let ec = 0; ec < m; ++ec) {
            if (prefix[er][ec] <= k) cnt++;
        }
    }
    // Return the count
    return cnt;
};

Count Submatrices with Top-Left Element and Sum Less Than k Complexity Analysis

Time Complexity: O(n × m)

Prefix Sum Construction

We construct a 2D prefix sum matrix where each element prefix[i][j] represents the sum of the submatrix from the top-left corner (0,0) to the cell (i,j) in the original grid.

  • This is done using two nested loops, each iterating over the dimensions of the grid:
    • Outer loop runs n times (rows)
    • Inner loop runs m times (columns)
  • Inside the nested loops, each prefix[i][j] is computed in constant time O(1) using:
    • prefix[i-1][j] (above cell)
    • prefix[i][j-1] (left cell)
    • prefix[i-1][j-1] (diagonal cell)
    • and adding grid[i][j]

Since each cell is processed exactly once and each operation inside is constant time, the total time for this step is: O(n × m)

Counting Valid Submatrices

  • After the prefix matrix is built, we iterate once more over all n × m cells.
  • For each cell prefix[i][j], we check whether the prefix sum is ≤ k.

Again:

  • Outer loop runs n times
  • Inner loop runs m times
  • Each operation (comparison and optional increment) is O(1)

So this step also takes: O(n × m)

Total Time Complexity

  • Prefix sum construction: O(n × m)
  • Count valid submatrices: O(n × m)

Thus, the overall time complexity is: O(n × m)

Space Complexity: O(n × m)

Auxiliary Space Complexity

Auxiliary space refers to the extra space used by the algorithm during execution, excluding the input and output.

  • A separate 2D vector prefix[n][m] is created to store the prefix sums.
  • It stores one integer per cell in the grid, so its space usage is:

No other significant data structures are used. Loop variables and counters (like cnt) use constant space.

Auxiliary Space Complexity is : O(n × m)

Total Space Complexity

Total space includes:

  1. Input space: The input matrix grid, of size n × m → O(n × m)
  2. Output space: A single integer cnt is returned → O(1)
  3. Auxiliary space: The prefix matrix → O(n × m)

So, if the input matrix grid has size n × m, its space is O(n × m).

Total Space = O(n × m) + O(1) + O(n × m) = O(n × m)

Similar Problems

Now we have successfully tackled this problem, let's try these similar problems:-

1. Count Submatrices With All Ones

Given an m x n binary matrix mat, return the number of submatrices that have all ones.

2. Number of Submatrices That Sum to Target

Given a matrix and a target, return the number of non-empty submatrices that sum to target.

A submatrix x1, y1, x2, y2 is the set of all cells matrix[x][y] with x1 <= x <= x2 and y1 <= y <= y2.

Two submatrices (x1, y1, x2, y2) and (x1', y1', x2', y2') are different if they have some coordinate that is different: for example, if x1 != x1'.

3. Max Sum of Rectangle No Larger Than K

Given an m x n matrix matrix and an integer k, return the max sum of a rectangle in the matrix such that its sum is no larger than k.

It is guaranteed that there will be a rectangle with a sum no larger than k.