Count of Interesting Subarrays
Problem Description:
You are given a 0-indexed integer array nums, an integer modulo, and an integer k.
Your task is to find the count of subarrays that are interesting.
A subarray nums[l..r] is interesting if the following condition holds:
Let cnt be the number of indices i in the range [l, r] such that nums[i] % modulo == k. Then, cnt % modulo == k.
Return an integer denoting the count of interesting subarrays.
Note: A subarray is a contiguous non-empty sequence of elements within an array.
Examples:
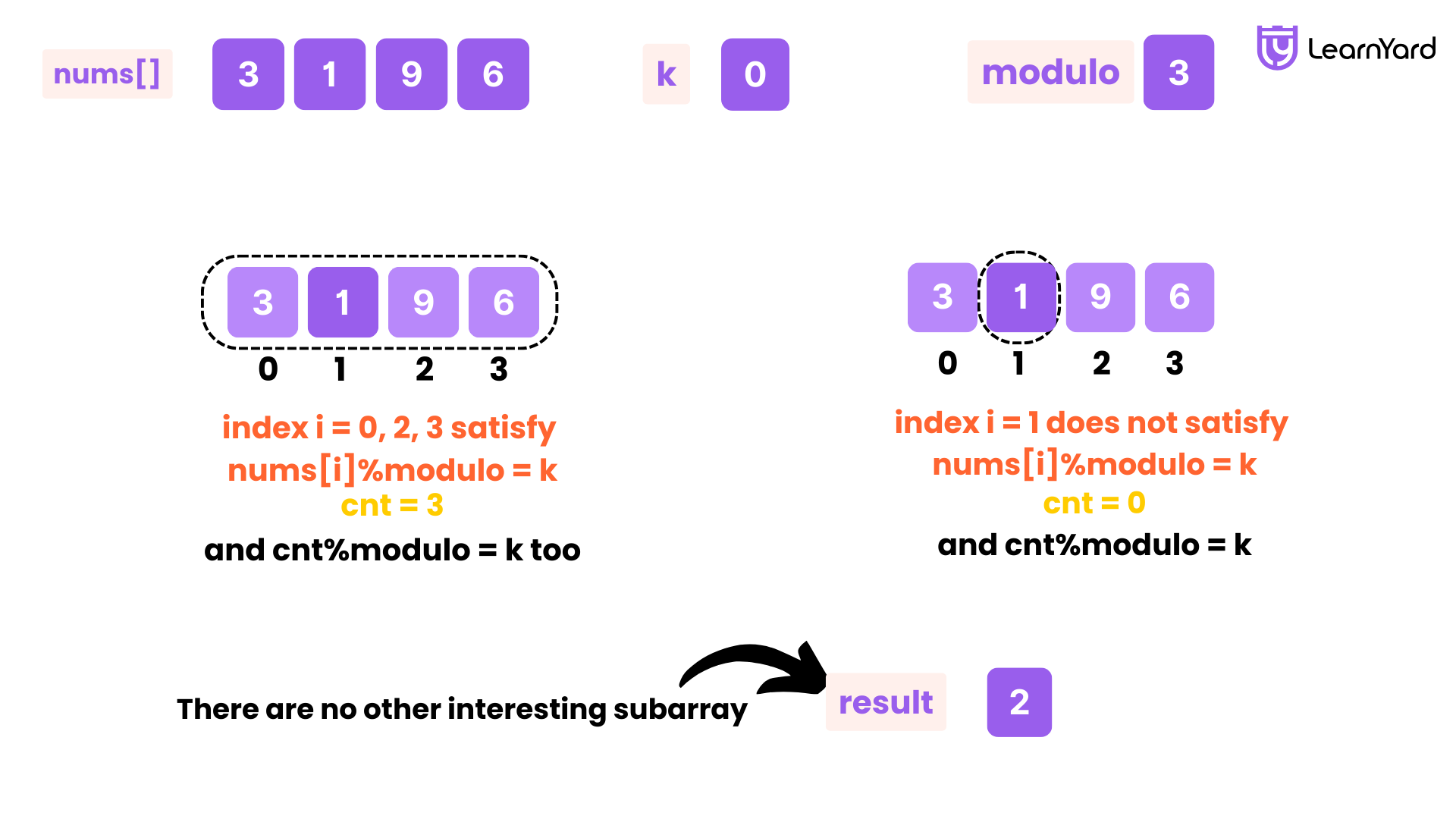
Input: nums = [3,1,9,6], modulo = 3, k = 0
Output: 2
Explanation: In this example the interesting subarrays are:
The subarray nums[0..3] which is [3,1,9,6]. There are three indices, i = 0, 2, 3, in the range [0, 3] that satisfy nums[i] % modulo == k. Hence, cnt = 3 and cnt % modulo == k.
The subarray nums[1..1] which is [1]. There is no index, i, in the range [1, 1] that satisfies nums[i] % modulo == k. Hence, cnt = 0 and cnt % modulo == k. It can be shown that there are no other interesting subarrays. So, the answer is 2.
Input: nums = [3,2,4], modulo = 2, k = 1
Output: 3
Explanation: In this example, the interesting subarrays are:
The subarray nums[0..0] which is [3]. There is only one index, i = 0, in the range [0, 0] that satisfies nums[i] % modulo == k. Hence, cnt = 1 and cnt % modulo == k.
The subarray nums[0..1] which is [3,2]. There is only one index, i = 0, in the range [0, 1] that satisfies nums[i] % modulo == k. Hence, cnt = 1 and cnt % modulo == k.
The subarray nums[0..2] which is [3,2,4]. There is only one index, i = 0, in the range [0, 2] that satisfies nums[i] % modulo == k. Hence, cnt = 1 and cnt % modulo == k. It can be shown that there are no other interesting subarrays. So, the answer is 3.
Constraints:
1 <= nums.length <= 10⁵
1 <= nums[i] <= 10⁹
1 <= modulo <= 10⁹
0 <= k < modulo
Brute Force Approach
When we read the problem statement, the first idea that comes to mind is simple:
We will go through each subarray and check if any element nums[i] % modulo is equal to k or not. If yes, we will increase cnt for that subarray. After updating cnt, we will check if cnt % modulo is equal to k or not. If yes, we will increase our answer. At the end, after checking each and every subarray, we will return the answer.
How to do it?
We can use a brute-force solution by traversing through the array.
- Iterate through all possible starting points of subarrays.
- For each starting point, iterate through all possible ending points to form subarrays.
- For each subarray, count the number of elements where nums[i] % modulo == k.
- Check if the count satisfies cnt % modulo == k.
- If the condition is met, increase the count of interesting subarrays.
- After evaluating all subarrays, return the final count.
Let's understand with an example:
Here’s a concise dry run for nums = [3, 1, 9, 6], modulo = 3, k = 0 using the brute force approach:
Iterating over the array:
- Subarray [3]:
Count (cnt) = 1 (only 3 satisfies nums[i] % modulo == k).
check if (cnt % modulo == k) → (1 % 3 != 0)
Not interesting. - Subarray [3, 1]:
Count (cnt) = 1.
check if (cnt % modulo == k) → 1 % 3 != 0.
Not interesting. - Subarray [3, 1, 9]:
Count (cnt) = 2 (3, 9 satisfy condition).
check if (cnt % modulo == k) → 2 % 3 != 0.
Not interesting. - Subarray [3, 1, 9, 6]:
Count (cnt) = 3 (3, 9, 6 satisfy condition).
check if (cnt % modulo == k) → 3 % 3 == 0.
Interesting. - Subarray [1]:
Count (cnt) = 0.
check if (cnt % modulo == k) → 0 % 3 == 0.
Interesting - Subarray [1, 9]:
Count (cnt) = 1
check if (cnt % modulo == k) → 1 % 3 != 0.
Not Interesting - Subarray [1, 9, 6]:
Count (cnt) = 2.
check if (cnt % modulo == k)→ 2 % 3 != 0.
Not Interesting - Subarray [9]:
Count (cnt) = 1
check if (cnt % modulo == k) → 1 % 3 != 0
Not Interesting - Subarray [9,6]:
Count (cnt) = 2.
check if (cnt % modulo == k) → 2 % 3 != 0
Not Interesting - Subarray [6]:
Count (cnt) = 1
check if (cnt % modulo == k) → 1 % 3 != 0
Not Interesting
Final Count of Interesting Subarrays: 2 (subarrays [3, 1, 9, 6] and [1]).
How to code it up:
- Initialize variables:
Get the size of the array (n).
Initialize ans to store the count of interesting subarrays. - Iterate through all starting points (i) of subarrays:
Start an outer loop from i = 0 to n - 1. - Iterate through all ending points (j) of subarrays:
Start an inner loop from j = i to n - 1. - Count elements satisfying the condition:
Check if nums[j] % modulo == k. If true, increment cnt. - Check if the subarray is interesting:
Verify if cnt % modulo == k. If true, increment ans. - Return the result:
After completing both loops, return ans.
Code Implementation
1. C++ Try on Compiler
class Solution {
public:
long long countInterestingSubarrays(vector<int>& nums, int modulo, int k) {
// Get the size of the array
int n = nums.size();
// Initialize the answer to store the count of interesting subarrays
long long ans = 0;
// Iterate through all starting points of subarrays
for (int i = 0; i < n; i++) {
// Initialize count for the current subarray
int cnt = 0;
// Iterate through all ending points of subarrays starting from i
for (int j = i; j < n; j++) {
// Check if nums[j] satisfies nums[j] % modulo == k
if (nums[j] % modulo == k)
// Increment count
cnt++;
// Check if the subarray is interesting
if (cnt % modulo == k)
// Increment the result
ans++;
}
}
// Return the total count of interesting subarrays
return ans;
}
};
2. Java Try on Compiler
class Solution {
public long countInterestingSubarrays(List<Integer> nums, int modulo, int k) {
// Get the size of the array
int n = nums.size(); // Use size() for List in Java
// Initialize the answer to store the count of interesting subarrays
long ans = 0;
// Iterate through all starting points of subarrays
for (int i = 0; i < n; i++) {
// Initialize count for the current subarray
int cnt = 0;
// Iterate through all ending points of subarrays starting from i
for (int j = i; j < n; j++) {
// Check if nums[j] satisfies nums[j] % modulo == k
// Use get() to access elements in List
if (nums.get(j) % modulo == k) {
// Increment count
cnt++;
}
// Check if the subarray is interesting
if (cnt % modulo == k) {
// Increment the result
ans++;
}
}
}
// Return the total count of interesting subarrays
return ans;
}
}
3. Python Try on Compiler
class Solution:
def countInterestingSubarrays(self, nums, modulo, k):
# Get the size of the array
n = len(nums)
# Initialize the answer to store the count of interesting subarrays
ans = 0
# Iterate through all starting points of subarrays
for i in range(n):
# Initialize count for the current subarray
cnt = 0
# Iterate through all ending points of subarrays starting from i
for j in range(i, n):
# Check if nums[j] satisfies nums[j] % modulo == k
if nums[j] % modulo == k:
# Increment count
cnt += 1
# Check if the subarray is interesting
if cnt % modulo == k:
# Increment the result
ans += 1
# Return the total count of interesting subarrays
return ans
4. Javascript Try on Compiler
/**
* @param {number[]} nums
* @param {number} modulo
* @param {number} k
* @return {number}
*/
var countInterestingSubarrays = function (nums, modulo, k) {
// Get the size of the array
const n = nums.length;
// Initialize the answer to store the count of interesting subarrays
let ans = 0;
// Iterate through all starting points of subarrays
for (let i = 0; i < n; i++) {
// Initialize count for the current subarray
let cnt = 0;
// Iterate through all ending points of subarrays starting from i
for (let j = i; j < n; j++) {
// Check if nums[j] satisfies nums[j] % modulo == k
if (nums[j] % modulo === k) {
// Increment count
cnt++;
}
// Check if the subarray is interesting
if (cnt % modulo === k) {
// Increment the result
ans++;
}
}
}
// Return the total count of interesting subarrays
return ans;
};Time Complexity: O(n²)
This approach runs two nested loops to find all subarrays, one inside another, where the outer loop runs n times
(i.e. i ranges from 0 to n), and for each iteration of the outer loop, the inner loop(i.e. j ranges from i to n) also runs n-i times.
Analyzing the Loops:
Outer Loop (indexed by i):
It runs from 0 to n-1. So, it iterates n times.
Inner Loop (indexed by j):
For each fixed i, j runs from i to n-1.
When i = 0, j runs n times.
When i = 1, j runs n-1 times.
When i = 2, j runs n-2 times.
…
When i = n-1, j runs 1 time.
Total Iterations:
To find the total number of iterations of the inner loop across all iterations of the outer loop,
we sum up the iterations for each value of i: ∑(i=0 to n−1) (n−i)
This is the sum of an arithmetic series: n+(n−1)+(n−2)+…+1.
If we closely observe and reverse the series
we get 1 + 2 + 3 + … + (n-2) + (n-1) + n.
That is nothing but the sum of n terms.
So the sum of n numbers from 1 to n is (n*(n+1))/2.
Thus, the total number of operations is (n*(n+1))/2.
Simplifying to Big-O Notation:
In Big-O notation, we focus on the term that grows the fastest as n increases, and we ignore constant factors and lower-order terms.
Therefore: O((n*(n+1))/2) ≈ O(n²)
Conclusion: The time complexity of the given code is O(n²).
This is because the nested loops result in a quadratic number of total operations, which dominate the runtime as the input size n becomes large.
Space Complexity: O(n)
Auxiliary Space Complexity: O(1)
The solution uses only a few variables (ans, cnt) are used, which require O(1) space.
Total Space Complexity: O(n)
The input array nums is given, which requires O(n) space.
Adding this to the auxiliary space gives: Total Space = O(n)
Will Brute Force Work Against the Given Constraints?
For the current solution, the time complexity is O(n²), which is not suitable for n ≤ 10⁵. This means that for each test case, where the size of the array is at most 10⁵, the solution might not execute within the given time limits.
Since O(n²) results in a maximum of 10¹⁰ operations (for n = 10⁵), the solution is not expected to work well for larger test cases. In most competitive programming environments, problems can handle up to 10⁶ operations per test case, meaning that for n ≤ 10⁵, the solution with 10¹⁰ operations is not efficient enough.
When multiple test cases are involved, the total number of operations could easily exceed this limit and approach 10¹⁰ operations, especially when there are many test cases or the value of n increases.
Thus, while the solution meets the time limits for a single test case, the O(n²) time complexity poses a risk for Time Limit Exceeded (TLE) errors when handling larger input sizes or multiple test cases. This can be a challenge for competitive programming problems with larger inputs or numerous test cases.
Can we optimize it?
Yes, of course!
We can definitely optimize it—let's do it!
In the previous approach, we iterated over each index and for every element, we made all the possible subarrays and counted their cnt values while checking if the subarray was interesting. This gave us a time complexity of O(n²), which is inefficient for large arrays.
Where are we lagging?
The inefficiency comes from the fact that for each index i, we are iterating over all subarrays starting from it and calculating the cnt for each subarray. This results in an O(n²) complexity.
Can we optimize this part?
Yes, we can optimize it, and here's how:
Suppose we have a subarray from index i to j.
- Let the cnt till i be cntᵢ and the cnt till j be cntⱼ.
- The difference (cntⱼ - cntᵢ) will give us the number of elements where nums[i] % modulo == k.
If the subarray is interesting, then (cntⱼ - cntᵢ) % modulo == k.
Using Modulo Properties:
Rearranging the equation:
(cntⱼ − cntᵢ) % modulo = k % modulo
cntⱼ % modulo − cntᵢ % modulo = k % modulo
Rearranging the equation:
cntᵢ % modulo = cntⱼ % modulo - k % modulo
We can simplify this to:
cntᵢ % modulo = (cntⱼ − k) % modulo
This means, for any index j, if there exists a previous index i such that:
cntᵢ % modulo = ( cntⱼ − k) % modulo
then there exists a subarray between the index i and j that is an interesting subarray.
Since k can be greater than cntⱼ, the expression (cntⱼ - k) can become negative. To avoid inconsistencies in modulo arithmetic, we will add modulo to ensure positive values.
For example:
Let cntⱼ = 2, k = 6, and modulo = 3.
Here, cntⱼ - k becomes:
2 - 6 = -4, which is negative.
Problem with Negative Values:
- In modulo arithmetic, negative results can create inconsistencies because different programming languages handle modulo operations with negative numbers differently:
- For example, in Python: -4 % 3 = 2.
- In some other languages like C++, -4 % 3 = -1.
- Negative values bring inconsistencies which, can lead to different hash values when using a hash map or dictionary. Since hash maps rely on consistent keys, this can cause incorrect results due to mismatched keys.
Resolution by Adding Modulo:
To resolve this, we add the modulo to ensure non-negative results:
(cntⱼ - k + modulo) % modulo
Substituting the values:
(2 - 6 + 3) % 3 = (-4 + 3) % 3 = -1 % 3 → 2.
Now, the value becomes 2, which is consistent and avoids any negative hash values, ensuring the program works correctly across all cases.
Thus, adding modulo guarantees that all values used as keys are non-negative, preventing errors in hash-based lookups and ensuring correct results.
This gives:
cntᵢ % modulo=(cntⱼ − k + modulo)%modulo
We will call this value target:
target = ( cntⱼ − k + modulo)%modulo
Now, let's frame the algorithm:
- We will iterate over nums and calculate the value of cnt as we go. If nums[i] % modulo == k, we increase cnt.
- We will store the frequency of each cnt % modulo value in a hashmap.
- At each step, if (cnt - k + modulo) % modulo exists in the hashmap, it means there was a previously encountered index i such that nums[i..j] forms an interesting subarray. In that case, we add all such potential subarrays to our answer.
- Final Answer: After iterating through the entire array, we return the final count of interesting subarrays.
By utilizing the modulo properties and the hashmap to track previously seen values of cnt % modulo, we can reduce the time complexity to O(n), making this approach much more efficient.
Let's understand with an example:
Let's walk through a concise dry run of the algorithm using nums = [3, 1, 9, 6], modulo = 3, k = 0.
- cnt = 0
- ans = 0
- mp = {0: 1} (We start by adding 0 with count 1 in the hashmap, as the initial cnt % modulo is 0).
Let's iterate through the array:
- Index i = 0 (nums[i] = 3):
nums[0] % 3 == 0, so cnt++ → cnt = 1.
target = (cnt - k + modulo) % modulo = (1 - 0 + 3) % 3 = 1.
mp.find(1): Not found in hashmap.
Update mp: mp[1] = 1. - Index i = 1 (nums[i] = 1):
nums[1] % 3 != 0, so cnt remains 1.
target = (cnt - k + modulo) % modulo = (1 - 0 + 3) % 3 = 1.
mp.find(1): Found with value 1.
Increment ans by 1 → ans = 1.
Update mp: mp[1] = 2. - Index i = 2 (nums[i] = 9):
nums[2] % 3 == 0, so cnt++ → cnt = 2.
target = (cnt - k + modulo) % modulo = (2 - 0 + 3) % 3 = 2.
mp.find(2): Not found in hashmap.
Update mp: mp[2] = 1. - Index i = 3 (nums[i] = 6):
nums[3] % 3 == 0, so cnt++ → cnt = 3.
target = (cnt - k + modulo) % modulo = (3 - 0 + 3) % 3 = 0.
mp.find(0): Found with value 1.
Increment ans by 1 → ans = 2.
Update mp: mp[0] = 2.
Final Output: 2
ans = 2: There are 2 interesting subarrays: [3, 1, 9, 6] and [1].
Thus, the final answer is 2.
How to code it up:
Here' the pseudo-code for the above approach:
Initialize:
- ans = 0
- cnt = 0
- mp = {0: 1} (base case)
Iterate through the array:
- For each i from 0 to n-1:
- If nums[i] % modulo == k, increment cnt.
- Update cnt %= modulo.
- Calculate target = (cnt - k + modulo) % modulo.
- If target is found in mp, increment ans by mp[target].
- Update mp[cnt]++.
- Return ans as the result.
Code Implementation
1. C++ Try on Compiler
class Solution {
public:
long long countInterestingSubarrays(vector<int>& nums, int modulo, int k) {
// Size of the array
int n = nums.size();
// To store the result (count of interesting subarrays)
long long ans = 0;
// To track the count of nums[i] % modulo == k
int cnt = 0;
// HashMap to store the frequency of cnt % modulo
unordered_map<int, int> mp;
// Initialize the map with the base case, 0: 1
mp[0] = 1;
for(int i = 0; i < n; i++) {
// If nums[i] satisfies the condition
if(nums[i] % modulo == k)
// Increment cnt
cnt++;
// Keep cnt within modulo
cnt %= modulo;
// Compute the target to check in the map
int target = (cnt - k + modulo) % modulo;
// If target exists in the map
if(mp.find(target) != mp.end())
// Add the count of previous occurrences of target to the answer
ans += mp[target];
// Update the frequency of cnt % modulo in the map
mp[cnt]++;
}
// Return the total count of interesting subarrays
return ans;
}
};
2. Java Try on Compiler
class Solution {
public long countInterestingSubarrays(List<Integer> nums, int modulo, int k) {
// Size of the array
int n = nums.size();
// To store the result (count of interesting subarrays)
long ans = 0;
// To track the count of nums[i] % modulo == k
int cnt = 0;
// HashMap to store the frequency of cnt % modulo
HashMap<Integer, Integer> mp = new HashMap<>();
// Initialize the map with the base case, 0: 1
mp.put(0, 1);
for (int i = 0; i < n; i++) {
// If nums[i] satisfies the condition
if (nums.get(i) % modulo == k)
// Increment cnt
cnt++;
// Keep cnt within modulo
cnt %= modulo;
// Compute the target to check in the map
int target = (cnt - k + modulo) % modulo;
// If target exists in the map
if (mp.containsKey(target))
// Add the count of previous occurrences of target to the answer
ans += mp.get(target);
// Update the frequency of cnt % modulo in the map
mp.put(cnt, mp.getOrDefault(cnt, 0) + 1);
}
// Return the total count of interesting subarrays
return ans;
}
}3. Python Try on Compiler
from collections import defaultdict
class Solution:
def countInterestingSubarrays(self, nums, modulo, k):
# Size of the array
n = len(nums)
# To store the result (count of interesting subarrays)
ans = 0
# To track the count of nums[i] % modulo == k
cnt = 0
# HashMap to store the frequency of cnt % modulo
mp = defaultdict(int)
# Initialize the map with the base case, 0: 1
mp[0] = 1
for i in range(n):
# If nums[i] satisfies the condition
if nums[i] % modulo == k:
# Increment cnt
cnt += 1
# Keep cnt within modulo
cnt %= modulo
# Compute the target to check in the map
target = (cnt - k + modulo) % modulo
# If target exists in the map
if target in mp:
# Add the count of previous occurrences of target to the answer
ans += mp[target]
# Update the frequency of cnt % modulo in the map
mp[cnt] += 1
# Return the total count of interesting subarrays
return ans
4. Javascript Try on Compiler
var countInterestingSubarrays = function(nums, modulo, k) {
// Size of the array
const n = nums.length;
// To store the result (count of interesting subarrays)
let ans = 0;
// To track the count of nums[i] % modulo == k
let cnt = 0;
// HashMap to store the frequency of cnt % modulo
const mp = new Map();
// Initialize the map with the base case, 0: 1
mp.set(0, 1);
for (let i = 0; i < n; i++) {
// If nums[i] satisfies the condition
if (nums[i] % modulo === k)
// Increment cnt
cnt++;
// Keep cnt within modulo
cnt %= modulo;
// Compute the target to check in the map
const target = (cnt - k + modulo) % modulo;
// If target exists in the map
if (mp.has(target))
// Add the count of previous occurrences of target to the answer
ans += mp.get(target);
// Update the frequency of cnt % modulo in the map
mp.set(cnt, (mp.get(cnt) || 0) + 1);
}
// Return the total count of interesting subarrays
return ans;
};
Time Complexity: O(n)
We loop through the array once, so this contributes O(n) where n is the length of the nums array.
Inside the loop, for each element nums[i], we perform the following operations:
- Checking if nums[i] % modulo == k: This is a constant time operation, O(1).
- Updating cnt and performing modulo operations: These are constant time operations, O(1).
- Calculating the target and checking the hashmap: Both operations are O(1) on average, as accessing and updating a hashmap (or unordered_map in C++) is O(1).
Since the loop runs n times, and each operation inside the loop is constant time O(1), the overall time complexity is: O(n)
Space Complexity: O(n)
- Auxiliary Space Complexity: O(n)
The only additional data structure used is the unordered_map (mp), which stores the frequency of cnt % modulo values. In the worst case, the map can store at most n distinct values if all elements in the array result in unique cnt % modulo values.
Therefore, the auxiliary space is O(n). - Total Space Complexity: O(n)
In addition to the input array, which is given as part of the problem and takes O(n) space, the total space usage includes the auxiliary space from the hashmap.
Thus, the total space complexity is O(n + n) = O(n).
Learning Tip
Now we have successfully tackled this problem, let's try these similar problems.
Given an array of integer nums and an integer k, return the total number of continuous subarrays whose sum equals k.
Given an integer array nums and an integer k, return the number of non-empty subarrays that have a sum divisible by k.
A subarray is a contiguous part of an array.