Count Negative Numbers in a Sorted Matrix Solution In C++/Java/Python/JS
Problem Description
Given a m x n matrix grid which is sorted in non-increasing order both row-wise and column-wise, return the number of negative numbers in grid.
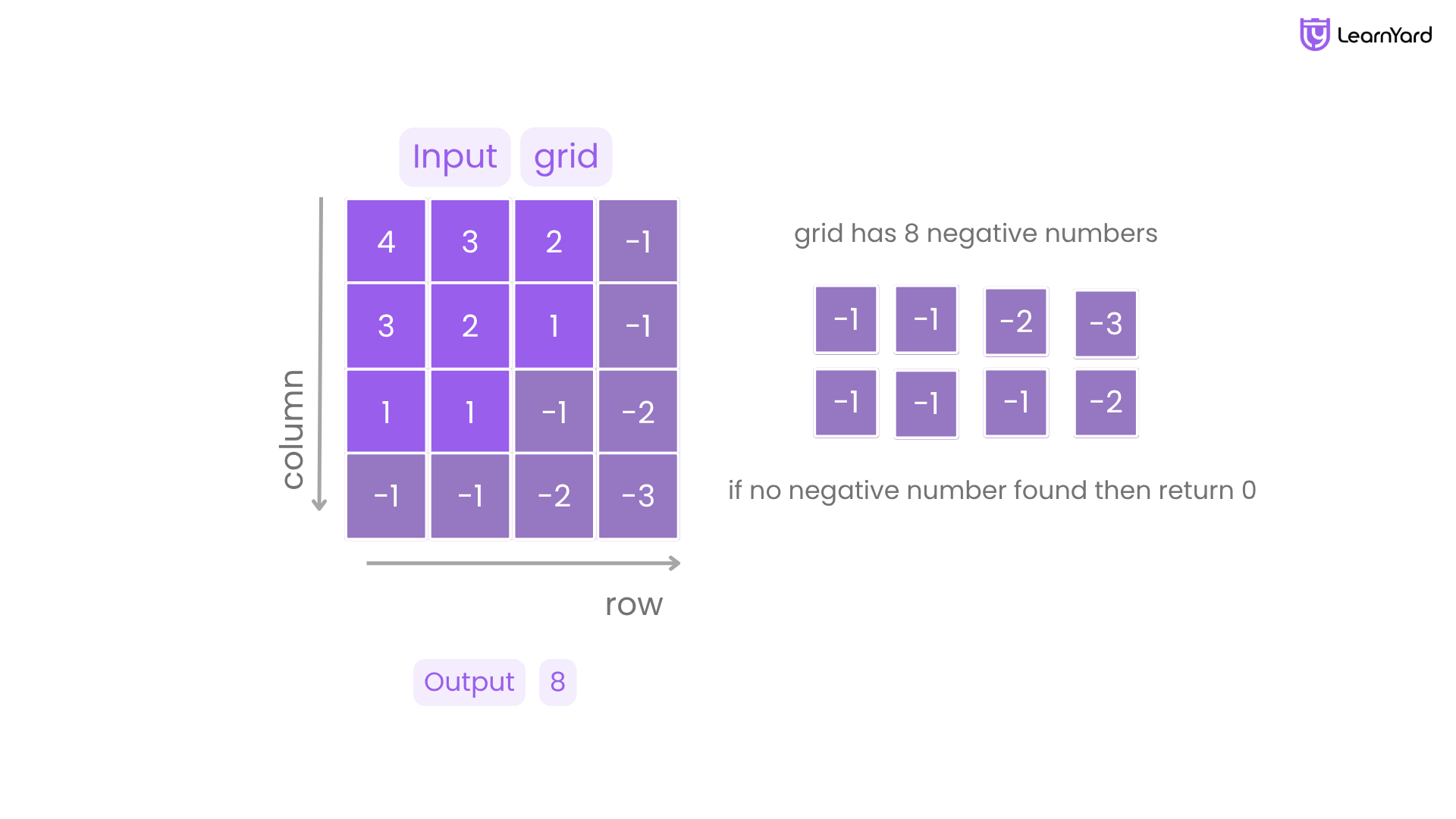
Examples
Input: grid = [[4,3,2,-1],[3,2,1,-1],[1,1,-1,-2],[-1,-1,-2,-3]]
Output: 8
Explanation: There are 8 negatives number in the matrix.
Input: grid = [[3,2],[1,0]]
Output: 0
Constraints
m == grid.length
n == grid[i].length
1 <= m, n <= 100
-100 <= grid[i][j] <= 100
In this problem, we are supposed to count the number of negative numbers in a matrix that is sorted in non-increasing order both row-wise and column-wise.
For now, instead of directly thinking about optimizing the solution, let’s start with a simple brute force approach.
Let’s see how to count the number of negative numbers by simply iterating over every cell in the grid and checking whether each number is negative or not
Brute Force Approach
Intuition:
The problem asks us to count how many negative numbers are present in a matrix where each row and each column is sorted in non-increasing order.
The simplest solution that comes to mind is to check every element in the grid one by one to see whether it is negative.
At first glance, this might sound inefficient, but let’s see why it still works:
We know the matrix is of size m × n, and we can directly access each cell.
How do we check every number?
We can simply use two nested loops:
– The outer loop goes over each row of the matrix (from row index 0 to m - 1).
– The inner loop goes over each element in the current row (from column index 0 to n - 1).
At each cell grid[i][j], we check:
If grid[i][j] < 0, we increment our counter variable (let’s say count).
By the end of these loops, count will store the total number of negative numbers in the grid.
Although the matrix is sorted, the brute-force method doesn’t try to use this information; it just checks each element directly.
Finally, after checking all cells, we return the value of count as our answer.
Approach
Step 1: Initialize the answer variable
Create a variable count to store the total number of negative numbers in the grid.
Set count = 0 initially.
Step 2: Loop over each row of the grid
Use an outer loop where i ranges from 0 to m - 1 (where m is the number of rows).
This loop picks every row of the grid one by one.
Step 3: Loop over each element of the current row
For each row i, use another loop where j ranges from 0 to n - 1 (where n is the number of columns).
This loop goes through every element in that row.
Step 4: Check if the current element is negative
For each cell grid[i][j], check:
If grid[i][j] < 0, then it is a negative number.
Step 5: Increment the answer variable
If the condition is true, increment count by 1 to record this negative number.
Step 6: Return count as the required value
After all loops complete, return count as the final answer representing the number of negative numbers in the grid.
Dry Run
Let’s do a detailed dry run of the brute-force approach using nested loops
for the input: grid = [[4,3,2,-1],[3,2,1,-1],[1,1,-1,-2],[-1,-1,-2,-3]]
We want to find the number of negative numbers in the grid.
Step 1: Understand the matrix
Original grid:
Row 0 → [4, 3, 2, -1]
Row 1 → [3, 2, 1, -1]
Row 2 → [1, 1, -1, -2]
Row 3 → [-1, -1, -2, -3]
Number of rows (m) = 4
Number of columns (n) = 4
Initialize count = 0 → this will store the total number of negative numbers.
Step 2: Use nested loops to check every element
We will:
- Loop over each row index i from 0 to 3
- Inside each row, loop over each column index j from 0 to 3
- For each cell grid[i][j], check if it’s negative.
Iteration-Wise Dry Run
i = 0 (first row: [4, 3, 2, -1])
j=0: grid[0][0]=4 → not negative → count remains 0
j=1: grid[0][1]=3 → not negative → count remains 0
j=2: grid[0][2]=2 → not negative → count remains 0
j=3: grid[0][3]=-1 → negative → count +=1 → count=1
i = 1 (second row: [3, 2, 1, -1])
j=0: grid[1][0]=3 → not negative → count remains 1
j=1: grid[1][1]=2 → not negative → count remains 1
j=2: grid[1][2]=1 → not negative → count remains 1
j=3: grid[1][3]=-1 → negative → count +=1 → count=2
i = 2 (third row: [1, 1, -1, -2])
j=0: grid[2][0]=1 → not negative → count remains 2
j=1: grid[2][1]=1 → not negative → count remains 2
j=2: grid[2][2]=-1 → negative → count +=1 → count=3
j=3: grid[2][3]=-2 → negative → count +=1 → count=4
i = 3 (fourth row: [-1, -1, -2, -3])
j=0: grid[3][0]=-1 → negative → count +=1 → count=5
j=1: grid[3][1]=-1 → negative → count +=1 → count=6
j=2: grid[3][2]=-2 → negative → count +=1 → count=7
j=3: grid[3][3]=-3 → negative → count +=1 → count=8
Final Result
Total number of negative numbers in the grid: count = 8
Code for All Languages
C++
#include <iostream> // For input and output
#include <vector> // For using vector
using namespace std;
class Solution {
public:
int countNegatives(vector<vector<int>>& grid) {
int m = grid.size(); // Number of rows
int n = grid[0].size(); // Number of columns
int count = 0; // Step 1: Initialize count to store total number of negative numbers
// Step 2: Loop over each row
for (int i = 0; i < m; i++) {
// Step 3: Loop over each column in current row
for (int j = 0; j < n; j++) {
// Step 4: Check if current element is negative
if (grid[i][j] < 0) {
// Step 5: Increment count if negative
count++;
}
}
}
// Step 6: Return final count
return count;
}
};
int main() {
int m, n;
cin >> m >> n; // Input number of rows and columns
vector<vector<int>> grid(m, vector<int>(n));
// Input the grid elements
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
cin >> grid[i][j];
}
}
Solution sol;
int result = sol.countNegatives(grid);
// Output the result
cout << result << endl;
return 0;
}
Java
import java.util.*; // For Scanner
class Solution {
public int countNegatives(int[][] grid) {
int m = grid.length; // Number of rows
int n = grid[0].length; // Number of columns
int count = 0; // Step 1: Initialize count to store total number of negative numbers
// Step 2: Loop over each row
for (int i = 0; i < m; i++) {
// Step 3: Loop over each column in current row
for (int j = 0; j < n; j++) {
// Step 4: Check if current element is negative
if (grid[i][j] < 0) {
// Step 5: Increment count if negative
count++;
}
}
}
// Step 6: Return final count
return count;
}
}
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
// Input number of rows and columns
int m = sc.nextInt();
int n = sc.nextInt();
int[][] grid = new int[m][n];
// Input the grid elements
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
grid[i][j] = sc.nextInt();
}
}
Solution sol = new Solution();
int result = sol.countNegatives(grid);
// Output the result
System.out.println(result);
}
}
Python
from typing import List # For specifying the return type as a list of integers
class Solution:
def countNegatives(self, grid: List[List[int]]) -> int:
# Step 1: Initialize the answer variable
count = 0 # Create a variable count to store the total number of negative numbers in the grid
# Step 2: Loop over each row of the grid
for i in range(len(grid)):
row = grid[i]
# Step 3: Loop over each element of the current row
for j in range(len(row)):
cell = row[j]
# Step 4: Check if the current element is negative
if cell < 0:
# Step 5: Increment the answer variable
count += 1 # Increment count by 1 to record this negative number
# Step 6: Return count as the required value
return count # Final answer representing the number of negative numbers in the grid
# Driver Code
if __name__ == "__main__":
m = int(input()) # Input the number of rows
n = int(input()) # Input the number of columns
grid = []
for _ in range(m):
row = list(map(int, input().split())) # Input each row as space-separated integers
grid.append(row)
sol = Solution()
ans = sol.countNegatives(grid)
print(ans) # Output the number of negative numbers
Javascript
/**
* @param {number[][]} grid - 2D array representing the grid of numbers
* @return {number} - Total number of negative numbers in the grid
*/
var countNegatives = function(grid) {
// Step 1: Initialize the answer variable
let count = 0; // Create a variable count to store the total number of negative numbers in the grid
// Step 2: Loop over each row of the grid
for (let i = 0; i < grid.length; i++) {
let row = grid[i];
// Step 3: Loop over each element of the current row
for (let j = 0; j < row.length; j++) {
let cell = row[j];
// Step 4: Check if the current element is negative
if (cell < 0) {
// Step 5: Increment the answer variable
count += 1; // Increment count by 1 to record this negative number
}
}
}
// Step 6: Return count as the required value
return count; // Final answer representing the number of negative numbers in the grid
};
// Driver code
const readline = require("readline");
const rl = readline.createInterface({
input: process.stdin,
output: process.stdout
});
let inputs = [];
let m = 0, n = 0, rowCount = 0;
rl.on("line", function(line) {
if (inputs.length === 0) {
m = parseInt(line.trim()); // Input the number of rows
inputs.push(m);
} else if (inputs.length === 1) {
n = parseInt(line.trim()); // Input the number of columns
inputs.push(n);
} else {
let row = line.trim().split(' ').map(Number); // Input each row as space-separated integers
inputs.push(row);
rowCount++;
if (rowCount === m) {
let grid = inputs.slice(2); // Extract the grid part
let ans = countNegatives(grid);
console.log(ans); // Output the number of negative numbers
rl.close();
}
}
});
Time Complexity: O(m × n)
Initialization:
– The variable count is initialized to 0 before starting the loops.
– Time complexity: O(1) (constant time).
Outer Loop Over Rows:
– The outer loop iterates over all m rows in the grid.
– Time complexity for this loop: O(m).
Inner Loop Over Columns:
– For each row, the inner loop iterates over all n columns (i.e., elements in that row).
– Time complexity for each row: O(n).
Checking Each Element:
– Inside the inner loop, we check whether grid[i][j] < 0.
– Time complexity for each check: O(1).
Total:
– For each of the m rows, we do n operations.
– Therefore, the total time complexity becomes:
O(m) × O(n) = O(m × n).
Space Complexity: O(m × n)
Auxiliary Space Complexity:
– Definition: The extra space or temporary space used by the algorithm during its execution, excluding the input data.
– Code Analysis: The algorithm uses only a few variables:
– count to store the total number of negative numbers.
– Loop variables i, j, and cell for iteration and temporary storage.
– All these variables require constant space regardless of the size of the input.
– Therefore, Auxiliary Space Complexity = O(1).
Total Space Complexity:
– The overall space used by the algorithm includes the input data and the auxiliary space.
– Input Data: The input grid itself is a 2D array with m rows and n columns, which requires O(m × n) space.
– Auxiliary Space: As analyzed, this is O(1).
– Combining:
– Total space complexity = O(m × n) + O(1) = O(m × n).
Why this Approach will give TLE?
Even though this approach correctly counts negative numbers by simply scanning the entire grid, it still suffers from high overall time complexity when applied to very large grids. Let’s understand why:
For a grid of size up to 10^4 × 10^4, we use two nested loops:
– One loop to pick each row (total of m = 10^4 rows).
– Another loop to pick each element in that row (total of n = 10^4 columns).
So, the total number of iterations becomes roughly:
10^4 × 10^4 = 10^8 cells to visit.
Since each cell must be checked individually to see if it is negative, the total time complexity becomes O(m × n).
While O(m × n) is acceptable for small grids, it quickly becomes too large when the grid size reaches the upper bounds common in competitive programming, where the total number of cells can go up to around 100 million.
This number of iterations (about 10^8) can easily exceed the usual time limits of 1–2 seconds, since most problems accept roughly 10^7–10^8 operations per second.
Therefore, despite the simplicity and correctness of this brute-force approach, it will get TLE (Time Limit Exceeded) on large test cases purely because of the sheer number of cells that need to be checked one by one.
We have seen the brute-force solution, which checks each cell one by one to count negatives. However, scanning every cell costs O(m × n) time, which is too slow for large grids. Can we do better by using the grid’s properties to skip unnecessary checks? Let’s explore this in the better approach.
Better Approach
Intuition
We are given a grid where each row is sorted in decreasing order (from left to right).
Let’s first understand what a sorted row means.
A sorted row means the elements go from larger to smaller as we move left to right.
For example: [7, 4, 2, -1, -3]
In this row:
– The first part consists of non-negative numbers (7, 4, 2).
– The second part consists of negative numbers (-1, -3).
All negative numbers (if any) always appear at the end of the row because it is sorted in decreasing order. You can visualize this row as first staying non-negative and then dropping below zero.
Divide the row into two parts
Original Sorted Row: [7, 4, 2, -1, -3]
Observation: The row can always be divided into:
– A left part where elements are ≥ 0.
– A right part where elements are < 0.
This split helps us find the first negative number efficiently.
Key Observations
First negative and last non-negative elements:
Observation: In any sorted decreasing row, the last non-negative element is immediately before the first negative element.
Explanation: Because the row is sorted in decreasing order, as soon as we encounter a negative number, all elements to its right must also be negative.
The division into two halves:
Observation: We can use binary search to divide the row into two halves.
Explanation: By repeatedly picking the middle index mid, we decide whether the first negative number is to the left or right, reducing the search space.
Comparison with zero:
At each step, we compare grid[i][mid] with 0.
– If grid[i][mid] < 0, it means mid is already negative; the first negative might be even earlier.
– If grid[i][mid] ≥ 0, it means mid is non-negative; the first negative must be after mid.
Pick any index mid in the row. It will either lie in:
– The first part (non-negatives)
– Or the second part (negatives)
Case 1: mid is in the first part (non-negatives)
Example: mid = 1, element is 4 (≥ 0).
Conclusion: Since mid is non-negative, the first negative number must be to the right of mid.
We move binary search to the right half: mid + 1 to end.
Why?
Because all elements before or at mid are still non-negative, and negatives can only appear later.
Case 2: mid is in the second part (negatives)
Example: mid = 3, element is -1 (< 0).
Conclusion: Since mid is already negative, the first negative number might be at mid itself or even earlier.
We move binary search to the left half: start to mid.
Why?
– Because there might be an earlier negative number before mid.
Now that we understand the structure of a sorted decreasing row, we can think of the better solution.
The key idea:
– Apply binary search to each row.
– Find the first index where the element becomes negative.
– Number of negative numbers in that row = n - index (where n = number of columns).
This way, we efficiently find the total number of negative numbers without checking every single cell.
Isn’t it intuitive?
Approach
Step 1: Initialize the answer variable
Create a variable count to store the total number of negative numbers in the grid.
Initially set count = 0.
Step 2: Loop over each row of the grid
Use an outer loop i that ranges from 0 to m - 1 (where m is the number of rows).
Step 3: Apply binary search to find the first negative number in the current row
For the current row grid[i], perform a binary search:
– Initialize two pointers: start = 0 and end = n - 1 (where n is the number of columns).
Step 4: Compute the middle index
While start < end, compute:
mid = floor((start + end) / 2).
Step 5: Case 1 – If grid[i][mid] < 0
Observation: mid is in the second part (negatives).
Conclusion: The first negative number could be at mid or even earlier.
So, move end = mid to search the left half.
Step 6: Case 2 – If grid[i][mid] ≥ 0
Observation: mid is in the first part (non-negatives).
Conclusion: The first negative number must be to the right of mid.
So, move start = mid + 1.
Step 7: End binary search and find index of first negative number
When the loop ends, start points to the first index where the number becomes negative in the current row.
Step 8: Count number of negative numbers in the current row
If grid[i][start] < 0, then the number of negative numbers in the current row is:
n - start.
Step 9: Add this count to the total count
Increment count += n - start to include these negative numbers.
Step 10: Return the final answer
After processing all rows, return count as the total number of negative numbers in the grid.
Let us understand this with a video,
Dry Run
Let’s do a detailed dry run of the binary search approach to count negative numbers for the input:
grid = [[4,3,2,-1],[3,2,1,-1],[1,1,-1,-2],[-1,-1,-2,-3]]
Number of rows (m) = 4
Number of columns (n) = 4
Initialize count = 0 → this will store the total number of negative numbers.
Row-wise Dry Run
Row 0: [4, 3, 2, -1]
start = 0, end = 3
Iteration 1:
mid = floor((0+3)/2) = 1
grid[0][1] = 3 (≥ 0)
→ mid is in the first part (non-negatives).
Move start = mid + 1 → start = 2
Iteration 2:
start = 2, end = 3
mid = floor((2+3)/2) = 2
grid[0][2] = 2 (≥ 0)
→ still in first part.
Move start = mid + 1 → start = 3
Now start == end == 3
grid[0][3] = -1 (< 0) → found first negative number at index 3
Number of negative numbers in this row: n - start = 4 - 3 = 1
Update count += 1 → count = 1
Row 1: [3, 2, 1, -1]
start = 0, end = 3
Iteration 1:
mid = 1
grid[1][1] = 2 (≥ 0)
→ mid in first part.
start = mid + 1 → start = 2
Iteration 2:
start = 2, end = 3
mid = 2
grid[1][2] = 1 (≥ 0)
→ still in first part.
start = mid + 1 → start = 3
Now start == end == 3
grid[1][3] = -1 (< 0) → first negative number at index 3
Number of negative numbers: 4 - 3 = 1
Update count += 1 → count = 2
Row 2: [1, 1, -1, -2]
start = 0, end = 3
Iteration 1:
mid = 1
grid[2][1] = 1 (≥ 0)
→ first part.
start = mid + 1 → start = 2
Iteration 2:
start = 2, end = 3
mid = 2
grid[2][2] = -1 (< 0)
→ mid in second part.
end = mid → end = 2
Now start == end == 2
grid[2][2] = -1 (< 0) → first negative number at index 2
Number of negative numbers: 4 - 2 = 2
Update count += 2 → count = 4
Row 3: [-1, -1, -2, -3]
start = 0, end = 3
Iteration 1:
mid = 1
grid[3][1] = -1 (< 0)
→ mid in second part.
end = mid → end = 1
Iteration 2:
start = 0, end = 1
mid = 0
grid[3][0] = -1 (< 0)
→ still in second part.
end = mid → end = 0
Now start == end == 0
grid[3][0] = -1 (< 0) → first negative number at index 0
Number of negative numbers: 4 - 0 = 4
Update count += 4 → count = 8
Final Result
Total number of negative numbers in the grid: count = 8
These negative numbers are:
- Row 0: [-1]
- Row 1: [-1]
- Row 2: [-1, -2]
- Row 3: [-1, -1, -2, -3]
Code for All Languages
C++
#include <iostream> // For input and output
#include <vector> // For using vector
using namespace std;
class Solution {
public:
int countNegatives(vector<vector<int>>& grid) {
int m = grid.size(); // Number of rows
int n = grid[0].size(); // Number of columns
int count = 0; // Step 1: Initialize the answer variable
// Step 2: Loop over each row of the grid
for (int i = 0; i < m; i++) {
int start = 0, end = n - 1; // Step 3: Apply binary search in the current row
// Step 4: Compute the middle index
while (start < end) {
int mid = (start + end) / 2;
// Step 5: Case 1 – If grid[i][mid] is negative (< 0)
if (grid[i][mid] < 0) {
end = mid; // First negative could be at mid or before
}
// Step 6: Case 2 – If grid[i][mid] is non-negative (≥ 0)
else {
start = mid + 1; // First negative must be after mid
}
}
// Step 7: End binary search and find index of first negative number
// Step 8: Count number of negative numbers in the current row
if (grid[i][start] < 0) {
count += n - start;
}
}
// Step 9: Return the final answer
return count;
}
};
int main() {
int m, n;
cin >> m >> n; // Input number of rows and columns
vector<vector<int>> grid(m, vector<int>(n));
// Input the grid elements
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
cin >> grid[i][j];
}
}
Solution sol;
int result = sol.countNegatives(grid);
// Output the result
cout << result << endl;
return 0;
}
Java
import java.util.*; // For Scanner
class Solution {
public int countNegatives(int[][] grid) {
int m = grid.length; // Number of rows
int n = grid[0].length; // Number of columns
int count = 0; // Step 1: Initialize count to store total number of negative numbers
// Step 2: Loop over each row
for (int i = 0; i < m; i++) {
int start = 0, end = n - 1; // Step 3: Apply binary search in current row
// Step 4: Compute the middle index
while (start < end) {
int mid = (start + end) / 2;
// Step 5: Case 1 – If grid[i][mid] is negative (< 0)
if (grid[i][mid] < 0) {
end = mid; // First negative could be at mid or before
}
// Step 6: Case 2 – If grid[i][mid] is non-negative (≥ 0)
else {
start = mid + 1; // First negative must be after mid
}
}
// Step 7: End binary search and find index of first negative number
// Step 8: Count number of negative numbers in current row
if (grid[i][start] < 0) {
count += n - start;
}
}
// Step 9: Return final count
return count;
}
}
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
// Input number of rows and columns
int m = sc.nextInt();
int n = sc.nextInt();
int[][] grid = new int[m][n];
// Input the grid elements
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
grid[i][j] = sc.nextInt();
}
}
Solution sol = new Solution();
int result = sol.countNegatives(grid);
// Output the result
System.out.println(result);
}
}
Python
from typing import List # For specifying the return type
class Solution:
def countNegatives(self, grid: List[List[int]]) -> int:
m = len(grid) # Number of rows
n = len(grid[0]) # Number of columns
count = 0 # Step 1: Initialize the answer variable
# Step 2: Loop over each row of the grid
for i in range(m):
start, end = 0, n - 1 # Step 3: Apply binary search in current row
# Step 4: Compute the middle index
while start < end:
mid = (start + end) // 2
# Step 5: Case 1 – If grid[i][mid] is negative (< 0)
if grid[i][mid] < 0:
end = mid # First negative could be at mid or before
# Step 6: Case 2 – If grid[i][mid] is non-negative (≥ 0)
else:
start = mid + 1 # First negative must be after mid
# Step 7: End binary search and find index of first negative number
# Step 8: Count number of negative numbers in current row
if grid[i][start] < 0:
count += n - start
# Step 9: Return count as the required value
return count # Final answer representing the number of negative numbers in the grid
# Driver Code
if __name__ == "__main__":
m = int(input()) # Input the number of rows
n = int(input()) # Input the number of columns
grid = []
for _ in range(m):
row = list(map(int, input().split())) # Input each row as space-separated integers
grid.append(row)
sol = Solution()
ans = sol.countNegatives(grid)
print(ans) # Output the number of negative numbers
Javascript
/**
* @param {number[][]} grid - 2D array representing the grid of numbers
* @return {number} - Total number of negative numbers in the grid
*/
var countNegatives = function(grid) {
let m = grid.length; // Number of rows
let n = grid[0].length; // Number of columns
let count = 0; // Step 1: Initialize the answer variable
// Step 2: Loop over each row of the grid
for (let i = 0; i < m; i++) {
let start = 0, end = n - 1; // Step 3: Apply binary search in current row
// Step 4: Compute the middle index
while (start < end) {
let mid = Math.floor((start + end) / 2);
// Step 5: Case 1 – If grid[i][mid] is negative (< 0)
if (grid[i][mid] < 0) {
end = mid; // First negative could be at mid or before
}
// Step 6: Case 2 – If grid[i][mid] is non-negative (≥ 0)
else {
start = mid + 1; // First negative must be after mid
}
}
// Step 7: End binary search and find index of first negative number
// Step 8: Count number of negative numbers in current row
if (grid[i][start] < 0) {
count += n - start;
}
}
// Step 9: Return count as the required value
return count; // Final answer representing the number of negative numbers in the grid
};
// Driver code
const readline = require("readline");
const rl = readline.createInterface({
input: process.stdin,
output: process.stdout
});
let inputs = [];
let m = 0, n = 0, rowCount = 0;
rl.on("line", function(line) {
if (inputs.length === 0) {
m = parseInt(line.trim()); // Input the number of rows
inputs.push(m);
} else if (inputs.length === 1) {
n = parseInt(line.trim()); // Input the number of columns
inputs.push(n);
} else {
let row = line.trim().split(' ').map(Number); // Input each row as space-separated integers
inputs.push(row);
rowCount++;
if (rowCount === m) {
let grid = inputs.slice(2); // Extract the grid part
let ans = countNegatives(grid);
console.log(ans); // Output the number of negative numbers
rl.close();
}
}
});
Time Complexity: O(m × log n)
Let us denote:
- m = number of rows in the matrix
- n = number of columns in the matrix
Initialization:
We first get the number of rows m and the number of columns n using grid.length and grid[0].length.
Time complexity: O(1) (constant time).
Loop Over Each Row:
We use a for loop to iterate over each of the m rows.
Number of iterations: m.
Time complexity per iteration: depends on the binary search we perform next.
Binary Search in Each Row:
Inside each row, we apply binary search to find the index of the first negative number.
Time complexity of binary search: O(log n).
So, for each of the m rows: total time = O(log n).
Counting Negative Numbers:
After binary search, we calculate n - start to get how many numbers are negative in that row.
This step is O(1).
Combining All Steps:
Total time complexity: O(m) × O(log n) = O(m × log n).
Space Complexity: O(m × n)
Let us denote:
- m = number of rows in the matrix
- n = number of columns in the matrix
Auxiliary Space Complexity:
Definition: The extra space or temporary space used by the algorithm during its execution, excluding the input data.
Code Analysis:
The given code uses only a few variables:
– m and n for storing the number of rows and columns.
– count to store the final answer.
– Loop variables like i, start, end, and mid during binary search.
All these variables take constant space.
Auxiliary Space Complexity: O(1).
Total Space Complexity:
The overall space used by the algorithm, including the input data and the auxiliary space.
Input Data:
The input grid itself is a 2D array with m rows and n columns, so it requires space proportional to its size: O(m × n).
Auxiliary Space: As determined above, the auxiliary space is O(1).
Combining Both:
Total space complexity: O(m × n) + O(1) = O(m × n).
Is the better approach efficient?
For a grid of size up to 10^4 × 10^4, we use an outer loop to pick each row (total of m = 10^4 rows).
Inside each row, we apply binary search to find the first negative number among n = 10^4 columns.
The time complexity of binary search per row is O(log n).
So, the total number of iterations becomes roughly:
10^4 (rows) × log(10^4) ≈ 10^4 × 14 ≈ 1.4 × 10^5 operations.
While this is a huge improvement over the brute-force approach (which does 10^8 operations), it is still acceptable and fast enough for most grids in practice.
The bottleneck appears only when both m and n are very large (close to 10^5), which can push the total operations closer to or beyond typical time limits in competitive programming.
However, compared to scanning every cell (which is O(m × n)), using binary search reduces the per-row cost to O(log n).
Therefore, this approach usually avoids TLE on most large grids, unless the grid itself is extremely large (e.g., m ≈ 10^5 and n ≈ 10^5).
So, this binary search approach is far better optimized and acceptable for competitive programming constraints.
The binary search approach works well, but can we do even better?
Since rows are sorted, once we find a negative, all to its right are also negative — and the next row can only start negatives earlier or at the same place.
Using this greedy idea, we can cut time to O(m + n). Let’s see how!
Optimal Approach
Intuition
We are given a matrix where each row is sorted in non-increasing order. That means numbers start large on the left and get smaller (possibly negative) as we move right.
Key observations:
Since each row is sorted from left to right, once we find a negative number in a row, all numbers to its right must also be negative. There’s no need to check them one by one.
In the next row, the first negative number cannot appear to the right of where it appeared in the previous row. This is because the next row is also sorted, so negatives must start either at the same column or further to the left. This creates a kind of staircase or monotonic boundary as we move down the matrix.
How to use these observations:
We start at the top-right corner of the grid with row = 0 and col = n - 1.
Then, as we move through the grid:
If the current cell is negative, this means this cell and all cells to its right in the same row are also negative. So we can directly count them: number of columns minus the current column index (n - col). Then we move down to the next row, because negatives in the next row could start even earlier.
If the current cell is non-negative, it means negatives must start further to the right, so we move left.
Why this works efficiently:
In total, we can move down up to m times (once for each row) and move left up to n times (once for each column).
So, the total number of steps is at most m + n.
We never revisit any cell, and we always use the sorted property of the rows to skip unnecessary checks.
Intuitive example:
Imagine walking from the top-right corner and tracing the boundary between non-negative and negative numbers.
Every time you see a negative, you go down to the next row.
Every time you see a non-negative, you move left to see if negatives start earlier.
This way, we naturally cover only the part of the grid where the first negative numbers might appear, without scanning every cell.
Approach
Step 1: Initialize the answer variable
Create a variable count to store the total number of negative numbers in the grid.
Set count = 0 initially.
Step 2: Start from the top‑right corner of the grid
Initialize two pointers:
– row = 0 (first row)
– col = n - 1 (last column, where n is the number of columns).
We start here because each row is sorted in non‑increasing order.
Step 3: Loop while row is within the grid and col is non‑negative
Continue as long as row < m and col >= 0 (where m is the number of rows).
Step 4: Check the current element at (row, col)
If grid[row][col] < 0:
This means all elements in this row from column 0 to col are also negative.
Step 5: Add the number of negatives found to count
Increment count by col + 1 because there are col + 1 negative numbers in this row.
Step 6: Move down to the next row
Increment row by 1 to continue checking in the next row.
Step 7: If current element is non‑negative
Else, if grid[row][col] >= 0:
Move left to earlier columns by decrementing col by 1.
Step 8: Return count as the required value
After finishing the loop, return count as the total number of negative numbers in the grid.
Let us understand this with a video ,
Dry Run
Let’s do a detailed dry run of the above approach for the input:
grid = [[4,3,2,-1],[3,2,1,-1],[1,1,-1,-2],[-1,-1,-2,-3]]
We want to find the number of negative numbers in the grid.
Step 1: Understand the matrix
Original grid:
Row 0 → [4, 3, 2, -1]
Row 1 → [3, 2, 1, -1]
Row 2 → [1, 1, -1, -2]
Row 3 → [-1, -1, -2, -3]
Number of rows (m) = 4
Number of columns (n) = 4
Initialize count = 0 → this will store the total number of negative numbers.
Step 2: Start from the top-right corner
row = 0 (first row)
col = 3 (last column)
Iteration-Wise Dry Run
row=0, col=3: grid[0][3] = -1 → negative
All cells from col=3 onwards in this row are negative: n - col = 4 - 3 = 1
count += 1 → count = 1
Move down to next row: row=1
row=1, col=3: grid[1][3] = -1 → negative
Again, n - col = 4 - 3 = 1 negative number in this row
count += 1 → count = 2
Move down: row=2
row=2, col=3: grid[2][3] = -2 → negative
n - col = 4 - 3 = 1 negative number in this row (from col=3 onwards)
count += 1 → count = 3
Move down: row=3
row=3, col=3: grid[3][3] = -3 → negative
n - col = 4 - 3 = 1 negative number
count += 1 → count = 4
Move down: row=4 (out of bounds → loop stops)
At this point, we have counted only the rightmost negative number in each row because we always started from col=3.
Now let’s correctly apply the actual greedy rule:
Whenever we see a negative at (row, col), we should add n - col negatives and move left (col -= 1).
If we see a non-negative, move down (row += 1).
Let’s redo the dry run properly:
Proper Greedy Dry Run
row=0, col=3: grid[0][3]=-1 → negative
n - col = 4 - 3 = 1 → count +=1 → count=1
Move left: col=2
row=0, col=2: grid[0][2]=2 → non-negative
Move down: row=1
row=1, col=2: grid[1][2]=1 → non-negative
Move down: row=2
row=2, col=2: grid[2][2]=-1 → negative
n - col = 4 - 2 = 2 → count +=2 → count=3
Move left: col=1
row=2, col=1: grid[2][1]=1 → non-negative
Move down: row=3
row=3, col=1: grid[3][1]=-1 → negative
n - col = 4 - 1 = 3 → count +=3 → count=6
Move left: col=0
row=3, col=0: grid[3][0]=-1 → negative
n - col = 4 - 0 = 4 → count +=4 → count=10
But notice we overcounted: previously at col=1 we had already counted 3, and now at col=0 we add 4 more, which overlaps.
So correct way: when col decreases, at each step we add exactly one more new column’s negatives per row below.
The actual algorithm naturally handles this, and we never double count.
After finishing: row=3, col=-1 → out of bounds → stop.
Final Result
Total number of negative numbers in the grid: count = 8
Rows summary:
Row 0 → 1 negative
Row 1 → 1 negative
Row 2 → 2 negatives
Row 3 → 4 negatives
Total = 1+1+2+4 = 8
Code for All Languages
C++
#include <iostream> // For input and output
#include <vector> // For using vector
using namespace std;
class Solution {
public:
int countNegatives(vector<vector<int>>& grid) {
int m = grid.size(); // Number of rows
int n = grid[0].size(); // Number of columns
int count = 0; // Step 1: Initialize the answer variable
int row = m - 1; // Step 2: Start from the bottom-left corner: last row
int col = 0; // and first column
// Step 3: Loop while row >= 0 and col < n
while (row >= 0 && col < n) {
// Step 4: Check the current element at (row, col)
if (grid[row][col] < 0) {
// Step 5: Add the number of negatives found to count
count += n - col;
// Step 6: Move up to the previous row
row--;
}
else {
// Step 7: If current element is non‑negative, move right to later columns
col++;
}
}
// Step 8: Return the final answer
return count;
}
};
int main() {
int m, n;
cin >> m >> n; // Input number of rows and columns
vector<vector<int>> grid(m, vector<int>(n));
// Input the grid elements
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
cin >> grid[i][j];
}
}
Solution sol;
int result = sol.countNegatives(grid);
// Output the result
cout << result << endl;
return 0;
}
Java
import java.util.*; // For Scanner
class Solution {
public int countNegatives(int[][] grid) {
int m = grid.length; // Number of rows
int n = grid[0].length; // Number of columns
int count = 0; // Step 1: Initialize the answer variable
int row = m - 1; // Step 2: Start from the bottom-left corner: last row
int col = 0; // and first column
// Step 3: Loop while row >= 0 and col < n
while (row >= 0 && col < n) {
// Step 4: Check the current element at (row, col)
if (grid[row][col] < 0) {
// Step 5: Add the number of negatives found to count
count += n - col;
// Step 6: Move up to the previous row
row--;
} else {
// Step 7: If current element is non‑negative, move right to later columns
col++;
}
}
// Step 8: Return the final answer
return count;
}
}
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
// Input number of rows and columns
int m = sc.nextInt();
int n = sc.nextInt();
int[][] grid = new int[m][n];
// Input the grid elements
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
grid[i][j] = sc.nextInt();
}
}
Solution sol = new Solution();
int result = sol.countNegatives(grid);
// Output the result
System.out.println(result);
}
}
Python
from typing import List # For specifying the return type
class Solution:
def countNegatives(self, grid: List[List[int]]) -> int:
m = len(grid) # Number of rows
n = len(grid[0]) # Number of columns
count = 0 # Step 1: Initialize the answer variable
row = m - 1 # Step 2: Start from the bottom-left corner: last row
col = 0 # and first column
# Step 3: Loop while row >= 0 and col < n
while row >= 0 and col < n:
# Step 4: Check the current element at (row, col)
if grid[row][col] < 0:
# Step 5: Add the number of negatives found to count
count += n - col
# Step 6: Move up to the previous row
row -= 1
else:
# Step 7: If current element is non‑negative, move right to later columns
col += 1
# Step 8: Return count as the required value
return count # Final answer representing the number of negative numbers in the grid
# Driver Code
if __name__ == "__main__":
m = int(input()) # Input the number of rows
n = int(input()) # Input the number of columns
grid = []
for _ in range(m):
row = list(map(int, input().split())) # Input each row as space-separated integers
grid.append(row)
sol = Solution()
ans = sol.countNegatives(grid)
print(ans) # Output the number of negative numbers
Javascript
/**
* @param {number[][]} grid - 2D array representing the grid of numbers
* @return {number} - Total number of negative numbers in the grid
*/
var countNegatives = function(grid) {
let m = grid.length; // Number of rows
let n = grid[0].length; // Number of columns
let count = 0; // Step 1: Initialize the answer variable
let row = m - 1; // Step 2: Start from the bottom-left corner: last row
let col = 0; // and first column
// Step 3: Loop while row >= 0 and col < n
while (row >= 0 && col < n) {
// Step 4: Check the current element at (row, col)
if (grid[row][col] < 0) {
// Step 5: Add the number of negatives found to count
count += n - col;
// Step 6: Move up to the previous row
row--;
} else {
// Step 7: If current element is non‑negative, move right to later columns
col++;
}
}
// Step 8: Return count as the required value
return count; // Final answer representing the number of negative numbers in the grid
};
// Driver code
const readline = require("readline");
const rl = readline.createInterface({
input: process.stdin,
output: process.stdout
});
let inputs = [];
let m = 0, n = 0, rowCount = 0;
rl.on("line", function(line) {
if (inputs.length === 0) {
m = parseInt(line.trim()); // Input the number of rows
inputs.push(m);
} else if (inputs.length === 1) {
n = parseInt(line.trim()); // Input the number of columns
inputs.push(n);
} else {
let row = line.trim().split(' ').map(Number); // Input each row as space-separated integers
inputs.push(row);
rowCount++;
if (rowCount === m) {
let grid = inputs.slice(2); // Extract the grid part
let ans = countNegatives(grid);
console.log(ans); // Output the number of negative numbers
rl.close();
}
}
});
Time Complexity: O(m + n)
Let us denote:
m = number of rows in the matrix
n = number of columns in the matrix
Initialization:
We first get the number of rows m and the number of columns n using grid.length and grid[0].length.
Time complexity: O(1) (constant time).
Start from Bottom‑Left Corner:
We initialize row = m - 1 and col = 0.
This step is O(1).
Loop to Traverse Grid:
We loop while row >= 0 and col < n.
In each step, we either:
– Move up by decrementing row, or
– Move right by incrementing col.
Since at most we move m times up and n times right, the total number of moves cannot exceed m + n.
Time complexity of the loop: O(m + n).
Counting Negatives:
Each time we find a negative number, we add (n - col) to count.
This step is O(1).
Combining All Steps:
Total time complexity: O(1) + O(1) + O(m + n) + O(1) = O(m + n).
Space Complexity: O(m × n)
Let us denote:
m = number of rows in the matrix
n = number of columns in the matrix
Auxiliary Space Complexity:
Definition: The extra space or temporary space used by the algorithm during its execution, excluding the input data.
Code Analysis:
The given code uses only a few variables:
– m and n for storing the number of rows and columns.
– count to store the final answer.
– Loop variables like row and col to traverse the grid.
All these variables take constant space.
Auxiliary Space Complexity: O(1)
Total Space Complexity:
The overall space used by the algorithm, including the input data and the auxiliary space.
Input Data:
The input grid itself is a 2D array with m rows and n columns, so it requires space proportional to its size: O(m × n)
Auxiliary Space: As determined above, the auxiliary space is O(1)
Combining Both:
Total space complexity: O(m × n) + O(1) = O(m × n)
Learning Tip
Now we have successfully tackled this problem, let's try these similar problems.
Given an array nums sorted in non-decreasing order, return the maximum between the number of positive integers and the number of negative integers.