Check Odd or Even Solution In C++/Java/Python/JS
Problem Description
Given a positive integer n, determine whether it is odd or even. Return true if the number is even and false if the number is odd.
Example
Input: n = 15
Output: false
Explanation: The number is not divisible by 2, Odd number.
Input: n = 44
Output: true
Explanation: The number is divisible by 2, Even number.
Constraints
- 1 <= n <= 10^4
Whenever we’re asked to check whether a number is even or odd, our first instinct might be to use the modulus operator — that’s a natural starting point. But let me give you a small hint before we dive in: what if I told you we could do this check without any division at all, by simply looking at the Binary Representation of the number? Let’s explore that idea together.
Optimal Approach
Intuition
When we want to check whether a number is even or odd, our first thought might be to use the modulus operator like n % 2 == 0. While this is correct, there's a faster and more efficient way using bitwise operators, specifically the bitwise AND operator (&).
What is Bitwise AND Operator?
The bitwise AND operator (symbol: &) works bit by bit on two numbers. Imagine you have two numbers, and you're comparing their binary forms — each bit of the first number is compared with the corresponding bit of the second number. The result is also a binary number. For each bit position:
- If both bits are 1, the result at that position is 1.
- If either or both bits are 0, the result at that position is 0.
In short:
1 & 1 = 1, but
1 & 0 = 0,
0 & 1 = 0,
0 & 0 = 0
Let’s understand with an example:
Take 5 & 3
- 5 in binary is 0101
- 3 in binary is 0011
Now we compare each bit from left to right:
0101 (which is 5)
& 0011 (which is 3)
= 0001 (which is 1)
So 5 & 3 = 1
To build the intuition, we must first understand how numbers are represented in binary. Every number is stored in memory as a sequence of bits (0s and 1s). Now here's the key observation: even numbers always end with a 0 in binary, and odd numbers always end with a 1. Why does this happen? Because the last bit in a binary number represents the 1’s place (2⁰). If that bit is 1, the number includes a 1 in its value — making it odd. If it’s 0, there’s no 1 added — making it even. For example:
- 4 → binary: 100, ends in 0 → even
- 5 → binary: 101, ends in 1 → odd
- 10 → binary: 1010, ends in 0 → even
- 15 → binary: 1111, ends in 1 → odd
So how do we check just that last bit? That’s where n & 1 comes in. The number 1 in binary is simply 000...0001, meaning only the last bit is set to 1. When we do n & 1, it checks whether the last bit in n is 1 or 0. If n & 1 == 0, the last bit is 0 → number is even → return true. If it gives 1, the last bit is 1 → number is odd → return false.
Detailed Explanation for (n & 1) Condition
Let’s recall the basic property of the AND operator:
- 1 & 1 = 1
- 1 & 0 = 0
- 0 & 1 = 0
- 0 & 0 = 0
This means AND only gives 1 if both bits are 1.
Now, if we write 1 in binary, it looks like this (assuming 4 bits for now):
0001
Notice how only the last bit is 1, and all other bits are 0.
So if we perform n & 1, what happens?
Let’s take n = 10 again, which is 1010 in binary.
Now do a bitwise AND:
1010 (binary of n)
& 0001 (binary of 1)
= 0000 (result)
Because all the other positions in 1 are 0, they will force all other bits of n to become 0. Only the last bit has a chance to survive — if and only if it is 1 in n. That’s why this operation isolates only the last bit of n.
If last bit of n is 0, then:
- n & 1 = 0 → number is even
If last bit of n is 1, then:
- n & 1 = 1 → number is odd
Approach
Step 1: Use Bitwise AND Operator to Check the Last Bit
We perform the expression (n & 1) inside the function.
The bitwise AND with 1 isolates the least significant bit of the number:
- If the last bit is 0, the number is even.
- If the last bit is 1, the number is odd.
Step 2: Return the Result Based on the Last Bit
We check if (n & 1) equals 0:
- If true, we return true indicating the number is even.
- Otherwise, we return false.
Dry Run
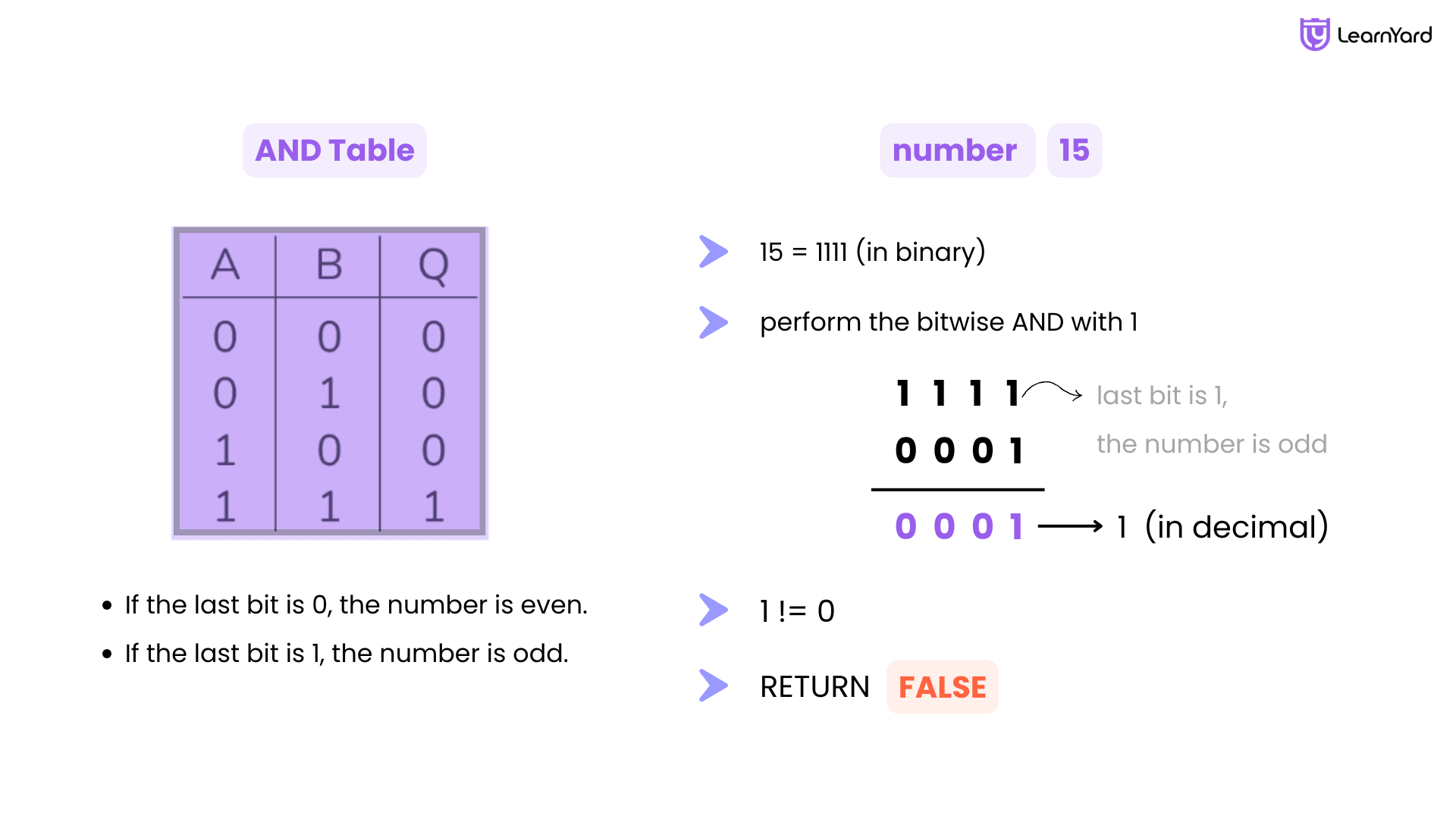
Let's do a detailed Dry Run to determine whether the number is even using the bitwise AND operator for the input:
n = 15
Step 1: Perform Bitwise AND Operation
We convert 15 to binary:
15 = 1111 (in binary)
Now we perform the bitwise AND with 1:
1111
0001
= 0001 → which is 1 in decimal
So, the result of (n & 1) is 1
Step 2: Compare with 0
Now we check:
1 == 0 → false
Hence, the function returns false
Final Result:
false
As 15 is an odd number.
Code for All Languages
C++
#include <iostream> // for cin and cout
using namespace std;
class Solution {
public:
// Function to check if a number is even using AND operator
bool isEven(int n) {
// Step 1: Use bitwise AND with 1 to check the last bit
// If the last bit is 0, the number is even
return (n & 1) == 0;
}
};
// Driver code
int main() {
int n;
// Input the number
cin >> n;
Solution sol;
bool result = sol.isEven(n);
// Output true if even, false if odd
cout << (result ? "true" : "false") << endl;
return 0;
}Java
import java.util.Scanner; // for taking input
class Solution {
// Function to check if a number is even using AND operator
static boolean isEven(int n) {
// Step 1: Use bitwise AND with 1 to check the last bit
// If the last bit is 0, the number is even
return (n & 1) == 0;
}
}
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n;
// Input the number
n = sc.nextInt();
boolean result = Solution.isEven(n);
// Output true if even, false if odd
System.out.println(result ? "true" : "false");
}
}
Python
class Solution:
# Function to check if a number is even using AND operator
def isEven(self, n):
# Step 1: Use bitwise AND with 1 to check the last bit
# If the last bit is 0, the number is even
return (n & 1) == 0
# Driver code
if __name__ == "__main__":
n = int(input())
sol = Solution()
result = sol.isEven(n)
# Output true if even, false if odd
print("true" if result else "false")
Javascript
class Solution {
// Function to check if a number is even using AND operator
isEven(n) {
// Step 1: Use bitwise AND with 1 to check the last bit
// If the last bit is 0, the number is even
return (n & 1) === 0;
}
}
// Driver code
const readline = require('readline');
const rl = readline.createInterface({
input: process.stdin,
output: process.stdout
});
rl.question('', function(n) {
n = parseInt(n);
const sol = new Solution();
const result = sol.isEven(n);
// Output true if even, false if odd
console.log(result ? "true" : "false");
rl.close();
});
Time Complexity: O(1)
Bitwise AND Operation: O(1)
The operation n & 1 is a bitwise operation.
It checks only the least significant bit of the binary representation of the number.
This operation does not depend on the size or value of n, and it executes in constant time.
Hence, the time complexity is O(1)
Comparison Operation: O(1)
After computing (n & 1), we compare the result with 0 using the equality operator ==.
This is a simple comparison and also takes constant time.
So, this step is also O(1)
Final Time Complexity: O(1)
- No loops, no recursion, no data structures dependent on input size
- All operations performed are constant time
Space Complexity: O(1)
Auxiliary Space Complexity: O(1)
This refers to the extra space used internally during the computation, excluding the input and output. In this program:
- The input value n is a single integer (already part of input, not counted as extra space)
- The function isEven uses only a single expression: (n & 1) == 0
- No variables, arrays, strings, or containers are created inside the function
- No additional memory is allocated during the execution
Hence, the auxiliary space required is constant, i.e., O(1)
Total Space Complexity: O(1)
This refers to the extra space used internally during the computation, including the input and output. In this program:
- There is no output array or string that grows with the size of the input
- The only output is a single boolean value: true or false
- The entire program uses only fixed-size variables (int and bool), and no dynamic storage
Therefore, the total space required also remains O(1).
Similar Problems
Given an integer n, return an array ans of length n + 1 such that for each i (0 <= i <= n), ans[i] is the number of 1's in the binary representation of i.
Given a positive integer n, write a function that returns the number of set bits in its binary representation.