Skip to main content

Array Basics

Check if an Array is Sorted

As we continue our progress in this article,  as arrays which is a fundamental data structure representing a collection of similar elements—it's essential to consider the array's organization, particularly whether it is sorted or unsorted. The state of sorting is a crucial property, as it directly influences the efficiency and feasibility of various algorithms and operations. For instance, determining whether an array is sorted is often a preliminary step before executing more complex tasks, such as binary search, where the correct functioning of the algorithm depends on the ordered arrangement of elements. Understanding whether an array is sorted allows us to make informed decisions about which algorithms to apply, thereby optimizing performance and ensuring accurate outcomes.

Write a program that takes an array as input and checks if it is sorted in forward order, backward order, or not sorted at all.

Example

Input: nums = [1, 2, 3, 4, 5]
Output: Sorted in Forward Order
Explanation: The array [1, 2, 3, 4, 5] is in ascending order, meaning it is sorted in forward order.

Input: nums = [5, 4, 3, 2, 1]
Output: Sorted in Backward Order
Explanation: The array [5, 4, 3, 2, 1] is in descending order, meaning it is sorted in backward order.

Input: nums = [3, 1, 4, 2, 5]
Output: Not Sorted
Explanation: The array [3, 1, 4, 2, 5] is neither in ascending nor descending order, so it is not sorted.

Approach

In this problem, we want to determine whether a given array is sorted in ascending order (forward order), descending order (backward order), or if it is not sorted at all. So there is an elementary logic to say whether an array is sorted in ascending or descending order or it is unsorted which is : 

  • Ascending Order (Forward Order): An array is in ascending order if each element is less than or equal to the next element. For example, [1, 2, 3, 4, 5] is in ascending order.
  • Descending Order (Backward Order): An array is in descending order if each element is greater than or equal to the next element. For example, [5, 4, 3, 2, 1] is in descending order.
  • Not Sorted: If an array does not follow either of the above rules, it is not sorted. For example, [3, 1, 4, 2, 5] is not sorted because it does not consistently increase or decrease.

From the above 3 points, we know the necessary conditions for an array to be sorted. An array will be sorted if and only if all its elements follow either the ascending order or the descending order condition. Therefore, if at any comparison either of the conditions is not met, the array will be considered unsorted.

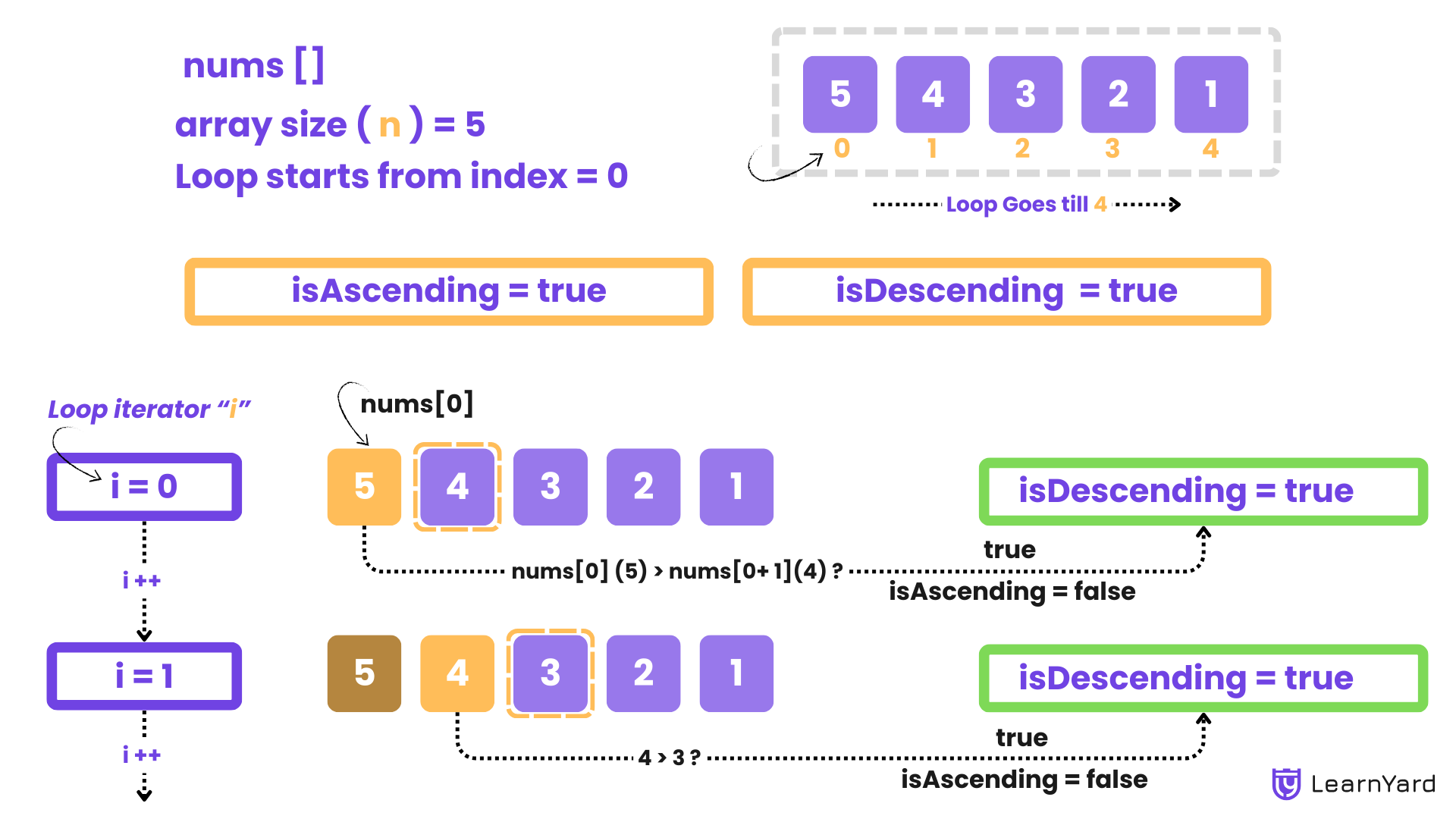
How do we know that a comparison failed in between?

For that we will declare 2 flags. These flags are booleans which help us track whether the array is in ascending or descending order as we go through it.

  • isAscending: We set this to true initially, assuming the array might be in ascending order. If for any comparison the condition is not satisfied we will change it to false.
  • isDescending: We set this to true initially, assuming the array might be in descending order. If for any comparison the condition is not satisfied we will change it to false.

Now we will start traversing the array

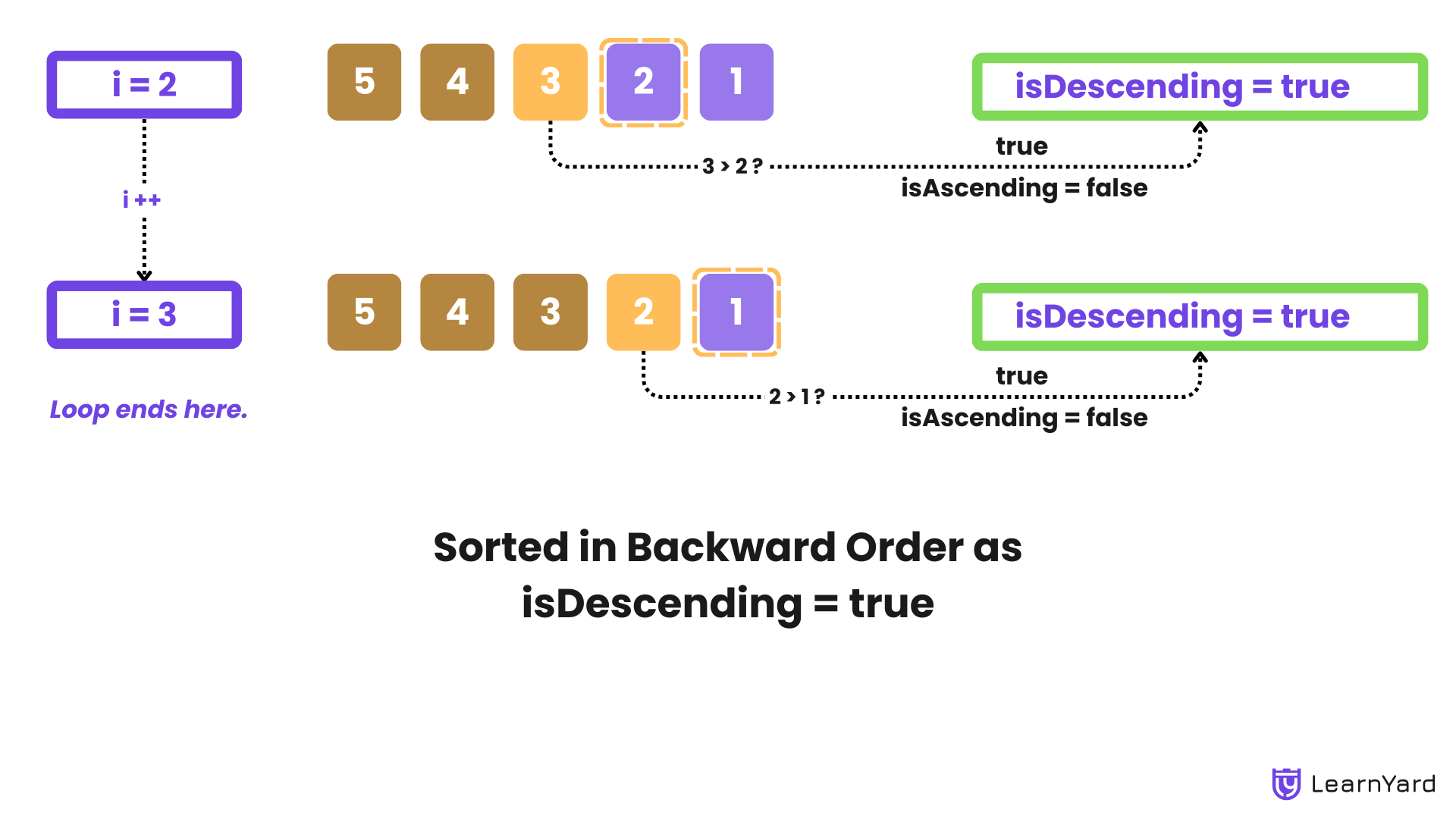
We use a loop to go through the array from the first element to the second-to-last element.

Why looping till second last index not the last index?

If the loop runs from 0 to n-1, the last iteration would attempt to compare the element at index n-1 with the element at index n, which does not exist. This would result in accessing memory out of bounds and potentially cause a runtime error.

For each element, we compare it with the next one:

  • Check for Ascending Order: If the current element is greater than the next one, it means the array is not in ascending order, so we set isAscending to false.
  • Check for Descending Order: If the current element is less than the next one, it means the array is not in descending order, so we set isDescending to false.
  • Why do we do this?: By checking both ascending and descending conditions as we move through the array, we can determine the array's order with a single pass.

After the loop finishes we will check the flags there are 3 possibilities for that

  • If isAscending is still true, the array is sorted in ascending (forward) order.
  • If isDescending is still true, the array is sorted in descending (backward) order.
  • If both flags are false, the array is not sorted.

Based on the flag’s values, we return or print whether the array is sorted in forward order, backward order, or not sorted at all.

Code for All Languages
C++ 
// Function to check if the array is sorted forward, backward, or not sorted
string checkSorted(int nums[], int size) {   
    // Initialize flags for ascending and descending order
    bool isAscending = true;
    bool isDescending = true;

    // Iterate through the array to check order
    for (int i = 0; i < size - 1; ++i) {
        // If current element is greater than the next, it's not ascending
        if (nums[i] > nums[i + 1]) {
            isAscending = false;
        }
        // If current element is smaller than the next, it's not descending
        if (nums[i] < nums[i + 1]) {
            isDescending = false;
        }
    }

    // Return results based on the flags
    if (isAscending) {
        return "Sorted in Forward Order";
    } else if (isDescending) {
        return "Sorted in Backward Order";
    } else {
        return "Not Sorted";
    }
}

Java 
public class CheckArraySorted {
    // Function to check if the array is sorted forward, backward, or not sorted
    static String checkSorted(int[] nums, int size) {
        // Initialize flags for ascending and descending order
        boolean isAscending = true;
        boolean isDescending = true;

        // Iterate through the array to check order
        for (int i = 0; i < size - 1; i++) {
            // If current element is greater than the next, it's not ascending
            if (nums[i] > nums[i + 1]) {
                isAscending = false;
            }
            // If current element is smaller than the next, it's not descending
            if (nums[i] < nums[i + 1]) {
                isDescending = false;
            }
        }

        // Return results based on the flags
        if (isAscending) {
            return "Sorted in Forward Order";
        } else if (isDescending) {
            return "Sorted in Backward Order";
        } else {
            return "Not Sorted";
        }
    }
}

Python 
# Function to check if the array is sorted forward, backward, or not sorted
def check_sorted(nums):
    # Initialize flags for ascending and descending order
    is_ascending = True
    is_descending = True

    # Iterate through the array to check order
    for i in range(len(nums) - 1):
        # If current element is greater than the next, it's not ascending
        if nums[i] > nums[i + 1]:
            is_ascending = False
        # If current element is smaller than the next, it's not descending
        if nums[i] < nums[i + 1]:
            is_descending = False

    # Return results based on the flags
    if is_ascending:
        return "Sorted in Forward Order"
    elif is_descending:
        return "Sorted in Backward Order"
    else:
        return "Not Sorted"

Javascript 
// Function to check if the array is sorted forward, backward, or not sorted
function checkSorted(nums) {
    // Initialize flags for ascending and descending order
    let isAscending = true;
    let isDescending = true;

    // Iterate through the array to check order
    for (let i = 0; i < nums.length - 1; i++) {
        // If current element is greater than the next, it's not ascending
        if (nums[i] > nums[i + 1]) {
            isAscending = false;
        }
        // If current element is smaller than the next, it's not descending
        if (nums[i] < nums[i + 1]) {
            isDescending = false;
        }
    }

    // Return results based on the flags
    if (isAscending) {
        return "Sorted in Forward Order";
    } else if (isDescending) {
        return "Sorted in Backward Order";
    } else {
        return "Not Sorted";
    }
}

// Read input size and elements
const size = parseInt(prompt());
const nums = Array.from({ length: size }, () => parseInt(prompt()));

// Call the function and log the result
console.log(checkSorted(nums));

Time Complexity: O(n)

The time complexity of this problem is O(n), where n is the number of elements in the array. 

This is because we traverse the array exactly once, comparing each element with the next one to check for ascending or descending order. Since the loop iterates from the first element to the second-to-last element, performing a constant-time comparison at each step, the total number of operations scales linearly with the size of the array.

Space Complexity : O(n)

  • Total Space Complexity: The total space complexity considers both the input space and any extra space used by the algorithm. For this problem, the total space complexity is O(n), where n is the number of elements in the input array. This is because the input array itself requires space proportional to its size.
  • Auxiliary Space Complexity: The auxiliary space complexity refers to the extra space required by the algorithm, excluding the input data. In this problem, the auxiliary space complexity is O(1) because we only use a fixed amount of extra space, regardless of the input array size.