Check If a String Contains All Binary Codes of Size K Solution In C++/Java/Python/JS
Problem Description
Given a binary string s and an integer k, return true if every binary code of length k is a substring of s. Otherwise, return false.
What is a Substring?
A substring is a continuous sequence of characters taken from a string, without changing their order.
For example, if the string is "abcde", then "abc", "bcd", and "de" are all valid substrings.
It must be contiguous, meaning we cannot skip characters (e.g., "ace" is not a substring).
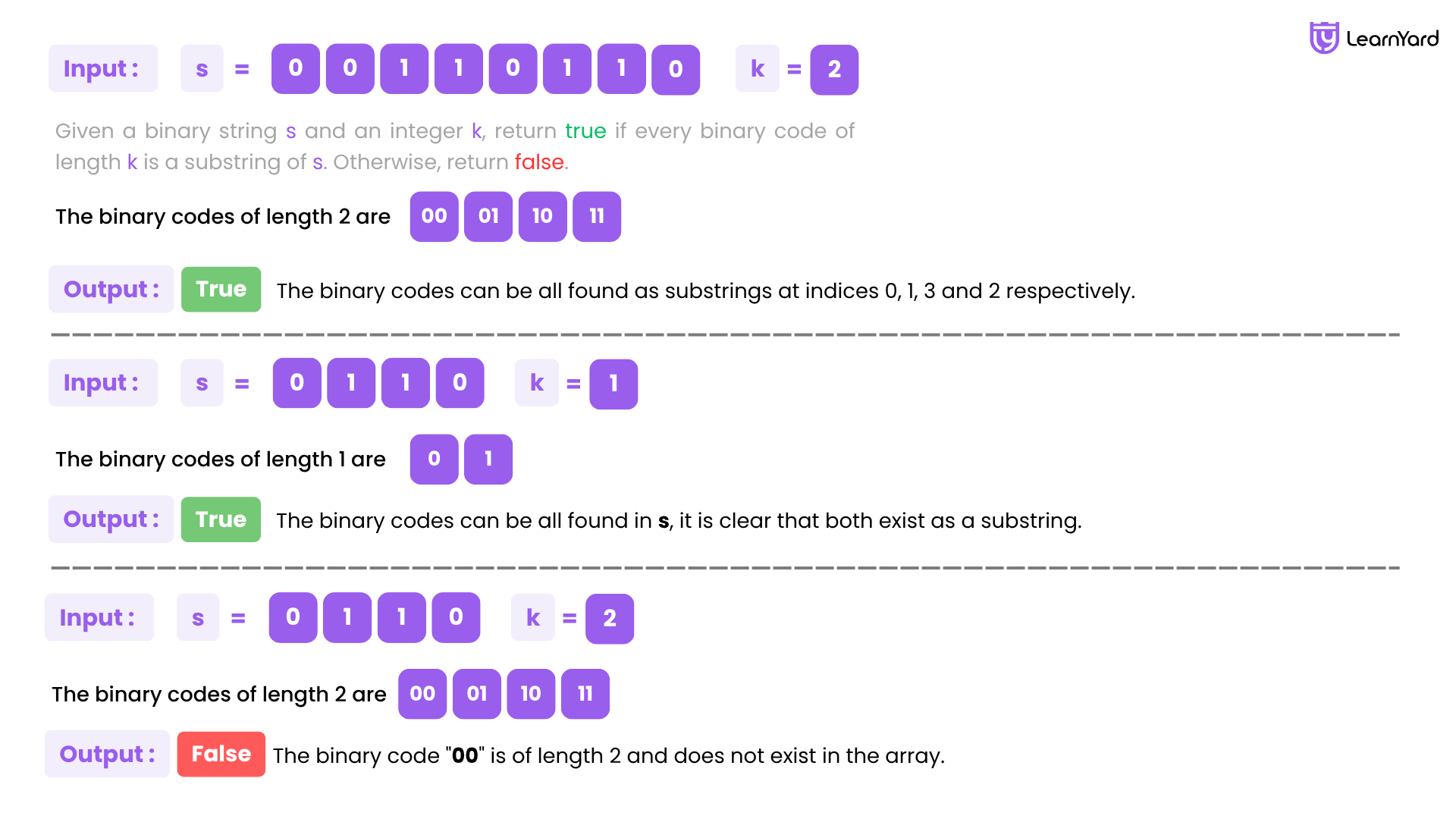
Example
Input: s = "00110110", k = 2
Output: true
Explanation: The binary codes of length 2 are "00", "01", "10" and "11". They can be all found as substrings at indices 0, 1, 3 and 2 respectively.
Input: s = "0110", k = 1
Output: true
Explanation: The binary codes of length 1 are "0" and "1", it is clear that both exist as a substring.
Input: s = "0110", k = 2
Output: false
Explanation: The binary code "00" is of length 2 and does not exist in the array.
Constraints
- 1 <= s.length <= 5 * 10^5
- s[i] is either '0' or '1'.
- 1 <= k <= 20
The very first question that comes to our mind after reading the problem is: How can we verify that every binary code of length k exists as a substring within the given string s?
A natural and straightforward approach is to consider every possible substring of length k and track which unique binary codes we have seen.
To build a strong foundation, let's first understand this brute-force solution step by step.
This will not only help us grasp the underlying logic clearly but also prepare us to appreciate more optimized approach later.
Brute-Force Approach
Intuition
We're given a binary string and an integer k, and we’re supposed to find out if all possible binary codes of length k appear as substrings inside that string. For example, if k = 2, then there are four possible combinations: "00", "01", "10", and "11". We need to see if each of these shows up somewhere in the string. A substring, remember, is a contiguous block of characters — so we cannot skip any characters in between.
Now, a natural idea that comes to mind is to look at every substring of length k and check what value it represents. For this, we can use a nested loop. The outer loop will fix the starting index of the substring, and the inner loop will help us build substrings of the same length as k from that starting point.
Generating Substrings of Length k Using Nested Loops
To solve problems involving fixed-length substrings, we start by identifying every substring of length k within the main string s. The most beginner-friendly way to do this is through nested loops.
We begin with an outer loop that fixes the starting index i of the substring. This loop runs from i = 0 to i = s.length() - k, ensuring we stay within bounds and form valid substrings.
For each fixed starting index i, we then use an inner loop to collect characters one by one and manually construct the substring. This inner loop runs from j = i to j < i + k. We initialize an empty string sub and append characters s[j] in sequence to build our desired substring of length k.
This approach not only helps us generate substrings without using any built-in functions but also strengthens our understanding of how index-based string manipulation works in a controlled manner.
Let’s go through an example.
Suppose s = "abcdefg" and k = 3. Then we generate:
- At i = 0, collect s[0], s[1], s[2] → "abc"
- At i = 1, collect s[1], s[2], s[3] → "bcd"
- At i = 2, collect s[2], s[3], s[4] → "cde"
- At i = 3, collect s[3], s[4], s[5] → "def"
- At i = 4, collect s[4], s[5], s[6] → "efg"
Each of these substrings is exactly of length 3. Once we have them, we can apply any logic we want — such as checking for patterns, calculating frequency, or comparing with another string.
But here's an observation: instead of storing the substrings themselves (which are strings and can take more space), we can convert each binary substring into its decimal equivalent (e.g., "11" becomes 3) and store it in a hash array.
What is a Hash Array?
A hash array (also called a hash table or boolean array in specific problems) is a simple and efficient way to track whether certain values have been seen or not. Think of it like a checklist. For each value we want to monitor, we create a box in our array. If we come across that value, we mark its box as true. If we never see it, the box stays false.
In the context of our problem (checking if all binary codes of length k exist in a string s), we use a boolean array of size 2^k, because there are exactly 2^k possible binary strings of length k. Each position in this array represents one possible binary code, converted into its decimal equivalent.n
Suppose k = 2, so the possible binary codes are:
- "00" → decimal 0
- "01" → decimal 1
- "10" → decimal 2
- "11" → decimal 3
So we create a hash array of size 4 (from 0 to 3):
hash = [false, false, false, false]
Now, as we extract each substring of length 2 from the given string s, we convert it into decimal and mark its position in the hash array as true:
- If we find "00" → mark hash[0] = true
- If we find "10" → mark hash[2] = true
- And so on...
At the end, if all entries in the hash array become true, it means we have found all binary codes of length k in the string. If even one is still false, it means that binary code was never found, and we return false.
This array tells us which codes we have already seen. Every time we find a new one, we mark it. The total number of such codes is 2^k, so if we find all of them, we return true. Otherwise, false.
Approach
Step 1: Calculate the Total Number of Possible Binary Codes of Length k
We calculate the total number of possible binary codes of length k as 2^k, which is implemented as 1 << k.
This gives us the number of unique binary codes we need to find as substrings in s.
Edge Case
Before we begin processing, we check if the length of the input string s is less than k.
If this is true, it means that we cannot form any binary code of length k from s because the string is too short.
In this case, we return false immediately to avoid unnecessary computations.
Note: Check for this edge case before Step 1
Step 2: Initialize a Hash Array to Track Found Codes
We create a boolean vector called hash of size 2^k initialized to false.
This array will be used to mark which binary codes (converted to decimal) have been found in the string.
We also initialize a variable count to zero to keep track of how many unique codes have been found so far.
Step 3: Iterate Over All Substrings of Length k in the String s
We use a loop to extract every substring of length k from the string s.
The loop runs from index 0 to len - k, ensuring that all valid substrings of length k are considered.
Step 4: Manually Construct Each Substring of Length k
For each starting index i, we create an empty string sub.
Then, using an inner loop from j = i to j < i + k, we append characters from s to sub to form the substring.
Step 5: Convert the Binary Substring to its Decimal Equivalent
We initialize an integer decimalValue to zero.
For each character in the substring sub, we shift decimalValue left by one bit and add the current binary digit (0 or 1).
This effectively converts the binary substring into its decimal representation.
Step 6: Mark the Decimal Value in the Hash Array if Not Already Marked
If hash[decimalValue] is false, it means this particular binary code hasn’t been found before.
We mark it as true and increment the count by one to record the newly found unique code.
Step 7: Return True Early if All Codes are Found
After marking a new code, we check if the count equals the total number of binary codes (2^k).
If yes, it means we have found all possible binary codes of length k as substrings in s.
In this case, we return true immediately without checking the remaining substrings.
Step 8: After Processing All Substrings, Return False if Not All Codes are Found
If after iterating through all substrings the count is still less than 2^k, it means some codes are missing.
Hence, we return false indicating that not all binary codes of length k exist as substrings in s.
Let us understand this with a video,
Dry Run
Let’s do a detailed dry run of the brute-force bitmasking approach for the input:
s = "00110110", k = 2
We want to check whether every binary code of length 2 exists as a substring in the string s.
Step 1: Initial Checks
- Length of string s = 8
- Value of k = 2
- Since 8 ≥ 2, we can proceed
- Total binary codes of length 2 = 2^2 = 4 → codes to find: "00", "01", "10", "11"
We initialize:
- A hash array of size 4 → hash = [false, false, false, false]
- A counter count = 0 to track how many unique codes we've seen
Step 2: Traverse All Substrings of Length k = 2
We'll loop from i = 0 to i = 6 (i.e., i ≤ s.length() - k)
Iteration-wise Dry Run
i = 0
- Build substring:
j = 0 → sub = "0"
j = 1 → sub = "00" - Convert to decimal:
"00" → 0 - hash[0] is false → mark it true and increment count
- hash = [true, false, false, false]
- count = 1
i = 1
- Build substring:
j = 1 → sub = "0"
j = 2 → sub = "01" - Convert to decimal:
"01" → 1 - hash[1] is false → mark it true and increment count
- hash = [true, true, false, false]
- count = 2
i = 2
- Build substring:
j = 2 → sub = "1"
j = 3 → sub = "11" - Convert to decimal:
"11" → 3 - hash[3] is false → mark it true and increment count
- hash = [true, true, false, true]
- count = 3
i = 3
- Build substring:
j = 3 → sub = "1"
j = 4 → sub = "10" - Convert to decimal:
"10" → 2 - hash[2] is false → mark it true and increment count
- hash = [true, true, true, true]
- count = 4
Now count equals totalCodes (4), so we return true immediately without checking remaining substrings.
Final Result
All 4 possible binary codes of length 2 were found as substrings at indices:
- "00" → index 0
- "01" → index 1
- "11" → index 2
- "10" → index 3
So the answer is: true
Explanation: The codes "00", "01", "10", and "11" were successfully detected inside the string. Since we found all required codes, the function returns true.
Code for All Languages
C++
#include <iostream> // for cin and cout
#include <string> // for using string
#include <vector> // for using vector<bool>
using namespace std;
class Solution {
public:
bool hasAllCodes(string s, int k) {
int len = s.length();
// Edge case: if the string is shorter than k, we can't form any k-length binary code
if (len < k) return false;
// Step 1: Total number of possible binary codes of length k = 2^k
int totalCodes = 1 << k;
// Step 2: Create a hash array of size 2^k to mark which codes are found
vector<bool> hash(totalCodes, false);
int count = 0; // To keep track of how many unique codes we've seen
// Step 3: Traverse all substrings of length k in the input string
for (int i = 0; i <= len - k; i++) {
string sub = "";
// Step 4: Manually construct a substring of length k starting at index i
for (int j = i; j < i + k; j++) {
sub.push_back(s[j]);
}
// Step 5: Convert the binary substring to its decimal value
int decimalValue = 0;
for (int idx = 0; idx < k; idx++) {
decimalValue = (decimalValue << 1) | (sub[idx] - '0');
}
// Step 6: If this code hasn't been marked before, mark it and increment count
if (!hash[decimalValue]) {
hash[decimalValue] = true;
count++;
}
// Step 7: If all possible codes are found early, return true immediately
if (count == totalCodes) {
return true;
}
}
// Step 8: After processing, if count is less than totalCodes, return false
return false;
}
};
// Driver code
int main() {
string s;
int k;
// Input binary string and integer k
cin >> s >> k;
Solution sol;
bool result = sol.hasAllCodes(s, k);
// Output result: true or false
cout << (result ? "true" : "false") << endl;
return 0;
}
Java
import java.util.Scanner; // for taking input
import java.util.Arrays; // for using arrays
class Solution {
public boolean hasAllCodes(String s, int k) {
int len = s.length();
// Edge case: if the string is shorter than k, we can't form any k-length binary code
if (len < k) return false;
// Step 1: Total number of possible binary codes of length k = 2^k
int totalCodes = 1 << k;
// Step 2: Create a hash array of size 2^k to mark which codes are found
boolean[] hash = new boolean[totalCodes];
int count = 0; // To keep track of how many unique codes we've seen
// Step 3: Traverse all substrings of length k in the input string
for (int i = 0; i <= len - k; i++) {
String sub = "";
// Step 4: Manually construct a substring of length k starting at index i
for (int j = i; j < i + k; j++) {
sub += s.charAt(j);
}
// Step 5: Convert the binary substring to its decimal value
int decimalValue = 0;
for (int idx = 0; idx < k; idx++) {
decimalValue = (decimalValue << 1) | (sub.charAt(idx) - '0');
}
// Step 6: If this code hasn't been marked before, mark it and increment count
if (!hash[decimalValue]) {
hash[decimalValue] = true;
count++;
}
// Step 7: If all possible codes are found early, return true immediately
if (count == totalCodes) {
return true;
}
}
// Step 8: After processing, if count is less than totalCodes, return false
return false;
}
}
// Driver code
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
String s = sc.next();
int k = sc.nextInt();
Solution sol = new Solution();
boolean result = sol.hasAllCodes(s, k);
// Output result: true or false
System.out.println(result ? "true" : "false");
}
}Python
class Solution:
def hasAllCodes(self, s: str, k: int) -> bool:
length = len(s)
# Edge case: if the string is shorter than k, we can't form any k-length binary code
if length < k:
return False
# Step 1: Total number of possible binary codes of length k = 2^k
total_codes = 1 << k
# Step 2: Create a hash array of size 2^k to mark which codes are found
hash_array = [False] * total_codes
count = 0 # To keep track of how many unique codes we've seen
# Step 3: Traverse all substrings of length k in the input string
for i in range(length - k + 1):
sub = ""
# Step 4: Manually construct a substring of length k starting at index i
for j in range(i, i + k):
sub += s[j]
# Step 5: Convert the binary substring to its decimal value
decimal_value = 0
for idx in range(k):
decimal_value = (decimal_value << 1) | (int(sub[idx]))
# Step 6: If this code hasn't been marked before, mark it and increment count
if not hash_array[decimal_value]:
hash_array[decimal_value] = True
count += 1
# Step 7: If all possible codes are found early, return true immediately
if count == total_codes:
return True
# Step 8: After processing, if count is less than total_codes, return false
return False
# Driver code
if __name__ == "__main__":
# Input binary string and integer k
s = input()
k = int(input())
sol = Solution()
result = sol.hasAllCodes(s, k)
# Output result: true or false
print("true" if result else "false")Javascript
/**
* @param {string} s - The input binary string
* @param {number} k - Length of binary codes to check
* @return {boolean} - True if all binary codes of length k exist as substrings, else false
*/
var hasAllCodes = function(s, k) {
const len = s.length;
// Edge case: if the string is shorter than k, we can't form any k-length binary code
if (len < k) return false;
// Step 1: Total number of possible binary codes of length k = 2^k
const totalCodes = 1 << k;
// Step 2: Create a hash array of size 2^k to mark which codes are found
const hash = new Array(totalCodes).fill(false);
let count = 0; // To keep track of how many unique codes we've seen
// Step 3: Traverse all substrings of length k in the input string
for (let i = 0; i <= len - k; i++) {
let sub = "";
// Step 4: Manually construct a substring of length k starting at index i
for (let j = i; j < i + k; j++) {
sub += s[j];
}
// Step 5: Convert the binary substring to its decimal value
let decimalValue = 0;
for (let idx = 0; idx < k; idx++) {
decimalValue = (decimalValue << 1) | (sub[idx] - '0');
}
// Step 6: If this code hasn't been marked before, mark it and increment count
if (!hash[decimalValue]) {
hash[decimalValue] = true;
count++;
}
// Step 7: If all possible codes are found early, return true immediately
if (count === totalCodes) {
return true;
}
}
// Step 8: After processing, if count is less than totalCodes, return false
return false;
};
// Driver code
const readline = require("readline");
const rl = readline.createInterface({
input: process.stdin,
output: process.stdout
});
let inputs = [];
rl.on("line", function (line) {
inputs.push(line.trim());
if (inputs.length === 2) {
const s = inputs[0];
const k = parseInt(inputs[1]);
const result = hasAllCodes(s, k);
console.log(result ? "true" : "false");
rl.close();
}
});Time Complexity: O(n * k)
Outer Loop: O(n - k + 1)
The outer loop runs from i = 0 to i = s.length() - k.
Let’s denote:
- n = length of the string s
- k = length of the binary codes we're checking
So, the loop runs approximately (n - k + 1) times, which is O(n) in the worst case.
Inner Loop to Build Substring: O(k)
For each iteration of the outer loop, we manually build a substring of length k using an inner loop.
This inner loop runs from j = i to j < i + k, and appends characters to the substring sub.
So, this step takes O(k) time.
Converting Binary to Decimal: O(k)
Once the substring is built, we convert it from binary to decimal using a loop that shifts and adds each bit.
This again takes O(k) time per substring.
Hash Table Access and Marking: O(1)
Accessing or updating the hash table using the decimal value is a constant time operation.
This step takes O(1) time.
Total Time per Outer Loop Iteration: O(k)
Each outer loop iteration involves:
- Building the substring → O(k)
- Converting to decimal → O(k)
- Hash check and update → O(1)
Total = O(k + k + 1) = O(k)
Final Time Complexity: O(n * k)
Since we do O(k) work for each of the O(n) valid starting positions in s,
the total time complexity becomes: O(n * k)
Where:
- n = length of the string s
- k = length of the binary codes
Space Complexity: O(2^k)
Auxiliary Space Complexity: O(2^k)
This refers to the extra space used by the algorithm that is independent of the input and output storage.
In our brute-force approach, we allocate:
- A hash array of size 2^k, where each index represents whether a particular binary code of length k has been seen
- A temporary string sub of size k, created in each iteration
- An integer decimalValue used for converting the substring to a numeric form
The most significant extra space is the hash table, which persists throughout the entire algorithm and is of size 2^k.
The temporary string and integer exist only during a single iteration and do not accumulate across iterations.
Therefore, the auxiliary space complexity is O(2^k).
Total Space Complexity: O(n + 2^k)
This includes the space required for:
- Input space: The input string s of length n occupies O(n) space
- Output space: The function returns a boolean value (true or false), which takes O(1) space
- Extra space used by the algorithm: As analyzed above, this is O(2^k) due to the hash table
Combining all space requirements:
Total Space Complexity = O(n) + O(2^k) + O(1) = O(n + 2^k)
We have seen the brute-force solution, which taught us how to check for every binary code of length k by exploring all substrings. However, checking each substring costs us extra O(k), which can be quite expensive. Is it possible to eliminate the nested loops and improve the time complexity? Let’s find out as we move on to the optimal approach.
Optimal Approach
Intuition
Previously, we solved this problem using a brute-force method where we manually built every substring of length k, converted it to decimal, and tracked which binary codes we had seen. While this works, it's inefficient — especially when the string s is large — because we’re repeatedly creating substrings and recalculating their values from scratch. Now let’s ask ourselves: Can we avoid recreating the same work over and over again?
Yes — by using a powerful idea known as the sliding window technique.
What is Sliding Window Technique?
Imagine you’re looking at a long line of items — like numbers in an array or letters in a string — and you want to examine small parts (subarrays or substrings) of it one at a time.
The Sliding Window Technique helps us do this efficiently, without starting over every time.
Instead of recalculating everything from scratch for each part, we slide a “window” over the data, reusing most of the previous work.
What is a “Window”?
A window is just a small segment or a range within the array or string.
For example:
Let’s say we have this array: arr = [1, 2, 3, 4, 5, 6]
If we want to look at subarrays of size 3:
- First window: [1, 2, 3]
- Next window: [2, 3, 4]
- Then: [3, 4, 5], and so on...
Each time, we just move the window one step forward, dropping the first element and including the next.
Why Do We Use It?
Because it's efficient!
Let’s say we wanted the sum of each window of size 3:
Naive Way (Brute Force):
- For every window, loop through the 3 elements and sum them → O(n * k), where n = length of array, k = window size.
Sliding Window Way:
Sum the first window once. For the next window:
- Subtract the element going out of the window.
- Add the element coming in.
This makes each new window sum in O(1) time → total O(n).
Types of Sliding Windows
There are mainly two types:
1. Fixed-size Sliding Window - Window size stays the same.
2. Variable-size Sliding Window - The window grows or shrinks based on conditions.
In this problem, we are using fixed size Sliding Window as the window size if fixed, i.e. length of p.
Instead of extracting and converting each new substring from scratch, we treat the binary string like a moving window. For example, suppose you have the substring "011", which has a decimal value of 3. When the window slides one character to the right, you now have "111", which you can compute by shifting the previous value and adding the new bit. You don’t need to build the whole substring again — just update it! That’s the power of using bit manipulation with a sliding window.
To make this work efficiently, we use a hash array (a boolean array of size 2^k) where each index represents a unique binary number of length k. We mark an index as true when we see that code in the string. If at any point the number of marked codes equals 2^k, we’ve found all possible binary codes — and we can return true right away.
So in essence, we:
- Use bit manipulation to slide the window forward and convert substrings to numbers in constant time.
- Use a hash array to track which codes have been seen.
- Use a counter to track how many unique codes we've found so far.
- Return early if we find all 2^k codes.
Approach
Step 1: Calculate the Total Number of Possible Binary Codes of Length k
We calculate the total number of possible binary codes of length k as 2^k, which is implemented as 1 << k.
This gives us the number of unique binary codes we need to find as substrings in s.
Edge Case
Before we begin processing, we check if the length of the input string s is less than k.
If this is true, it means we cannot form any binary code of length k from s because the string is too short.
In this case, we return false immediately to avoid unnecessary computations.
Note: Always perform this check before proceeding to Step 1.
Step 2: Initialize a Hash Array to Track Found Codes
We create a boolean vector called hash of size 2^k initialized to false.
This array helps us mark which binary codes (in decimal form) have been found in the string.
We also declare a variable count initialized to 0, which keeps track of how many unique binary codes we have found so far.
Step 3: Build the First Binary Window of Length k
Before starting the sliding window, we process the first k characters of the string to build the first window.
We initialize windowValue to 0 and, for each character from index 0 to k - 1, we left-shift windowValue and add the binary digit (s[i] - '0').
This constructs the decimal equivalent of the first k-length binary substring.
Step 4: Mark the First Window in the Hash Array
Once we get the decimal value of the first binary window, we mark its corresponding index in the hash array as true.
We also increment count to indicate that we have found our first unique binary code.
Step 5: Start Sliding the Window from Index k to End
Now we slide the window one character at a time starting from index k to the end of the string.
In each step, we remove the leftmost bit and add the new bit at the end to maintain the window size as k.
This is done using bitwise operations:
windowValue = ((windowValue << 1) & ((1 << k) - 1)) | (s[i] - '0')
Step 6: Mark the New Binary Code if Not Already Found
After updating the window, we check if hash[windowValue] is false.
If yes, it means this binary code hasn't been seen before, so we mark it as true and increment count.
Step 7: Return True Early if All Codes Are Found
After marking each new code, we check if count == totalCodes.
If this condition is met, it means we’ve successfully found all 2^k binary codes of length k.
We return true immediately without processing further.
Step 8: Return False if Not All Codes Were Found
If we finish sliding through the string and count < totalCodes, then not all binary codes were found.
In this case, we return false at the end of the function.
Let us understand this with a video,
Dry Run
Let’s do a detailed dry run of the sliding window bitmasking approach for the input:
s = "00110110", k = 2
We want to check whether every binary code of length 2 exists as a substring in the string s.
Step 1: Initial Checks
Length of string s = 8
Value of k = 2
Since 8 ≥ 2, we can proceed.
Total binary codes of length 2 = 2^2 = 4 → codes to find: "00", "01", "10", "11"
We initialize:
- A hash array of size 4 → hash = [false, false, false, false]
- A counter count = 0 to track how many unique codes we've seen
- A variable windowValue = 0
Step 2: Build the First Window of Length k
i = 0
s[0] = '0' → windowValue = (0 << 1) | 0 = 0
i = 1
s[1] = '0' → windowValue = (0 << 1) | 0 = 0
→ First k-length window = "00" → decimal = 0
Mark hash[0] = true, increment count = 1
hash = [true, false, false, false]
Step 3: Slide the Window from Index k to End
i = 2
s[2] = '1'
windowValue = ((0 << 1) & 3) | 1 = (0 & 3) | 1 = 1
→ New window = "01" → decimal = 1
hash[1] is false → mark it true, count = 2
hash = [true, true, false, false]
i = 3
s[3] = '1'
windowValue = ((1 << 1) & 3) | 1 = (2 & 3) | 1 = 2 | 1 = 3
→ New window = "11" → decimal = 3
hash[3] is false → mark it true, count = 3
hash = [true, true, false, true]
i = 4
s[4] = '0'
windowValue = ((3 << 1) & 3) | 0 = (6 & 3) | 0 = 2
→ New window = "10" → decimal = 2
hash[2] is false → mark it true, count = 4
hash = [true, true, true, true]
Now count = totalCodes = 4, so we return true immediately without checking remaining characters.
Final Result
All 4 possible binary codes of length 2 were found as substrings at indices:
- "00" → index 0
- "01" → index 1
- "11" → index 2
- "10" → index 3
So the answer is: true
Explanation: The codes "00", "01", "10", and "11" were successfully detected inside the string. Since we found all required codes, the function returns true.
Code for All Languages
C++
#include <iostream> // for cin and cout
#include <string> // for using string
#include <vector> // for using vector<bool>
using namespace std;
class Solution {
public:
bool hasAllCodes(string s, int k) {
int len = s.length();
// Edge case: if the string is shorter than k, we can't form any k-length binary code
if (len < k) return false;
// Step 1: Total number of possible binary codes of length k = 2^k
int totalCodes = 1 << k;
// Step 2: Create a hash array of size 2^k to mark which codes are found
vector<bool> hash(totalCodes, false);
int count = 0; // To keep track of how many unique codes we've seen
// Step 3: Use sliding window technique to extract binary codes of length k
int windowValue = 0;
// Step 4: Build the first window of size k
for (int i = 0; i < k; i++) {
windowValue = (windowValue << 1) | (s[i] - '0');
}
// Step 5: Mark the first window
hash[windowValue] = true;
count++;
// Step 6: Slide the window from index k to end
for (int i = k; i < len; i++) {
// Slide the window by removing the leftmost bit and adding the new rightmost bit
windowValue = ((windowValue << 1) & ((1 << k) - 1)) | (s[i] - '0');
// Step 7: If the new binary code hasn't been seen before, mark it
if (!hash[windowValue]) {
hash[windowValue] = true;
count++;
}
// Step 8: If all possible codes are found, return true early
if (count == totalCodes) {
return true;
}
}
// Step 9: After sliding, if not all codes were found, return false
return false;
}
};
// Driver code
int main() {
string s;
int k;
// Input binary string and integer k
cin >> s >> k;
Solution sol;
bool result = sol.hasAllCodes(s, k);
// Output result: true or false
cout << (result ? "true" : "false") << endl;
return 0;
}Java
import java.util.Scanner; // for taking input
class Solution {
public boolean hasAllCodes(String s, int k) {
int len = s.length();
// Edge case: if the string is shorter than k, we can't form any k-length binary code
if (len < k) return false;
// Step 1: Total number of possible binary codes of length k = 2^k
int totalCodes = 1 << k;
// Step 2: Create a hash array of size 2^k to mark which codes are found
boolean[] hash = new boolean[totalCodes];
int count = 0; // To keep track of how many unique codes we've seen
// Step 3: Use sliding window technique to extract binary codes of length k
int windowValue = 0;
// Step 4: Build the first window of size k
for (int i = 0; i < k; i++) {
windowValue = (windowValue << 1) | (s.charAt(i) - '0');
}
// Step 5: Mark the first window
hash[windowValue] = true;
count++;
// Step 6: Slide the window from index k to end
for (int i = k; i < len; i++) {
// Slide the window by removing the leftmost bit and adding the new rightmost bit
windowValue = ((windowValue << 1) & ((1 << k) - 1)) | (s.charAt(i) - '0');
// Step 7: If the new binary code hasn't been seen before, mark it
if (!hash[windowValue]) {
hash[windowValue] = true;
count++;
}
// Step 8: If all possible codes are found, return true early
if (count == totalCodes) {
return true;
}
}
// Step 9: After sliding, if not all codes were found, return false
return false;
}
}
// Driver class
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
// Input binary string and integer k
String s = sc.next();
int k = sc.nextInt();
Solution sol = new Solution();
boolean result = sol.hasAllCodes(s, k);
// Output result: true or false
System.out.println(result ? "true" : "false");
}
}
Python
class Solution:
def hasAllCodes(self, s: str, k: int) -> bool:
len_s = len(s)
# Edge case: if the string is shorter than k, we can't form any k-length binary code
if len_s < k:
return False
# Step 1: Total number of possible binary codes of length k = 2^k
totalCodes = 1 << k
# Step 2: Create a hash array of size 2^k to mark which codes are found
hash = [False] * totalCodes
count = 0 # To keep track of how many unique codes we've seen
# Step 3: Use sliding window technique to extract binary codes of length k
windowValue = 0
# Step 4: Build the first window of size k
for i in range(k):
windowValue = (windowValue << 1) | (int(s[i]))
# Step 5: Mark the first window
hash[windowValue] = True
count += 1
# Step 6: Slide the window from index k to end
for i in range(k, len_s):
# Slide the window by removing the leftmost bit and adding the new rightmost bit
windowValue = ((windowValue << 1) & ((1 << k) - 1)) | int(s[i])
# Step 7: If the new binary code hasn't been seen before, mark it
if not hash[windowValue]:
hash[windowValue] = True
count += 1
# Step 8: If all possible codes are found, return true early
if count == totalCodes:
return True
# Step 9: After sliding, if not all codes were found, return false
return False
# Driver code
if __name__ == "__main__":
s = input()
k = int(input())
sol = Solution()
result = sol.hasAllCodes(s, k)
# Output result: true or false
print("true" if result else "false")Javascript
/**
* @param {string} s
* @param {number} k
* @return {boolean}
*/
var hasAllCodes = function(s, k) {
let len = s.length;
// Edge case: if the string is shorter than k, we can't form any k-length binary code
if (len < k) return false;
// Step 1: Total number of possible binary codes of length k = 2^k
let totalCodes = 1 << k;
// Step 2: Create a hash array of size 2^k to mark which codes are found
let hash = new Array(totalCodes).fill(false);
let count = 0; // To keep track of how many unique codes we've seen
// Step 3: Use sliding window technique to extract binary codes of length k
let windowValue = 0;
// Step 4: Build the first window of size k
for (let i = 0; i < k; i++) {
windowValue = (windowValue << 1) | (s[i] - '0');
}
// Step 5: Mark the first window
hash[windowValue] = true;
count++;
// Step 6: Slide the window from index k to end
for (let i = k; i < len; i++) {
// Slide the window by removing the leftmost bit and adding the new rightmost bit
windowValue = ((windowValue << 1) & ((1 << k) - 1)) | (s[i] - '0');
// Step 7: If the new binary code hasn't been seen before, mark it
if (!hash[windowValue]) {
hash[windowValue] = true;
count++;
}
// Step 8: If all possible codes are found, return true early
if (count === totalCodes) {
return true;
}
}
// Step 9: After sliding, if not all codes were found, return false
return false;
};
// Driver code
const readline = require('readline');
const rl = readline.createInterface({
input: process.stdin,
output: process.stdout
});
let inputLines = [];
rl.on('line', function (line) {
inputLines.push(line.trim());
if (inputLines.length === 2) {
const s = inputLines[0];
const k = parseInt(inputLines[1]);
const result = hasAllCodes(s, k);
// Output result: true or false
console.log(result ? "true" : "false");
rl.close();
}
});Time Complexity: O(n)
Initial Window Construction: O(k)
Before starting the sliding process, we build the first window of size k by processing the first k characters of the string.
Each character is used once in a bitwise operation to update the current window value.
So, the time taken for this initial step is O(k).
Sliding Window Loop: O(n - k)
The main loop runs from i = k to i < n, where n is the length of the string.
So, the total number of iterations is approximately (n - k).
Let’s denote:
n = length of the input string s
k = length of the binary codes we’re checking
Operations Inside Each Iteration:
- Bit Manipulation to Update Window:
Each time, we perform bitwise shift and masking to maintain the k-length binary window.
These operations are constant-time and do not depend on k.
Time = O(1) - Hash Array Access and Update:
We check and update the boolean hash array at the computed decimal index.
Time = O(1)
So, total time per iteration = O(1)
Total Time for Sliding Phase: O(n - k)
Since we do O(1) work for each of the (n - k) iterations,
the total time taken by the sliding process is O(n - k)
Final Time Complexity: O(n)
- Initial Window Construction: O(k)
- Sliding Window Loop: O(n - k)
- Overall: O(k + (n - k)) = O(n)
Where:
n = length of the string s
k = length of the binary codes
Space Complexity: O(2^k)
Auxiliary Space Complexity: O(2^k)
This refers to the extra space used by the algorithm that is independent of the input and output storage.
In our sliding window approach, we create:
- A hash array of size 2^k to track which binary codes of length k have been seen.
- A few constant-sized variables such as windowValue, totalCodes, count, etc.
No additional dynamic data structures (like sets or substrings) are created during iteration.
All operations are done using bit manipulation, and the memory used is fixed based on k.
Therefore, the auxiliary space complexity is O(2^k).
Total Space Complexity: O(n + 2^k)
This includes the space required for:
- Input space: The input string s of length n takes O(n) space.
- Output space: Since we return only a boolean value (true or false), this takes O(1) space.
- Extra space: As analyzed above, the hash array takes O(2^k) auxiliary space.
Combining all space requirements:
Total Space Complexity = O(n) + O(1) + O(2^k) = O(n + 2^k)
Learning Tip
Now we have successfully tackled this problem, let's try these similar problems.
Given two strings s and p, return an array of all the start indices of p's anagrams in s. You may return the answer in any order.
Given a string s and an integer k, return the maximum number of vowel letters in any substring of s with length k. Vowel letters in English are 'a', 'e', 'i', 'o', and 'u'.