Capacity To Ship Packages Within D Days Solution In C++/Java/Python/JS
Problem Description:
A conveyor belt has packages that must be shipped from one port to another within D days.
The ith package on the conveyor belt has a weight of weights[i]. Each day, we load the ship with packages on the conveyor belt (in the order given by weights). We may not load more weight than the maximum weight capacity of the ship.
Return the least weight capacity of the ship that will result in all the packages on the conveyor belt being shipped within D days.
Examples:
Input: weights = [1,2,3,4,5,6,7,8,9,10], D = 5
Output: 15
Explanation: A ship capacity of 15 is the minimum to ship all the packages in 5 days like this:
1st day: 1, 2, 3, 4, 5
2nd day: 6, 7
3rd day: 8
4th day: 9
5th day: 10
Note that the cargo must be shipped in the order given, so using a ship of capacity 14 and splitting the packages into parts like (2, 3, 4, 5), (1, 6, 7), (8), (9), (10) is not allowed.
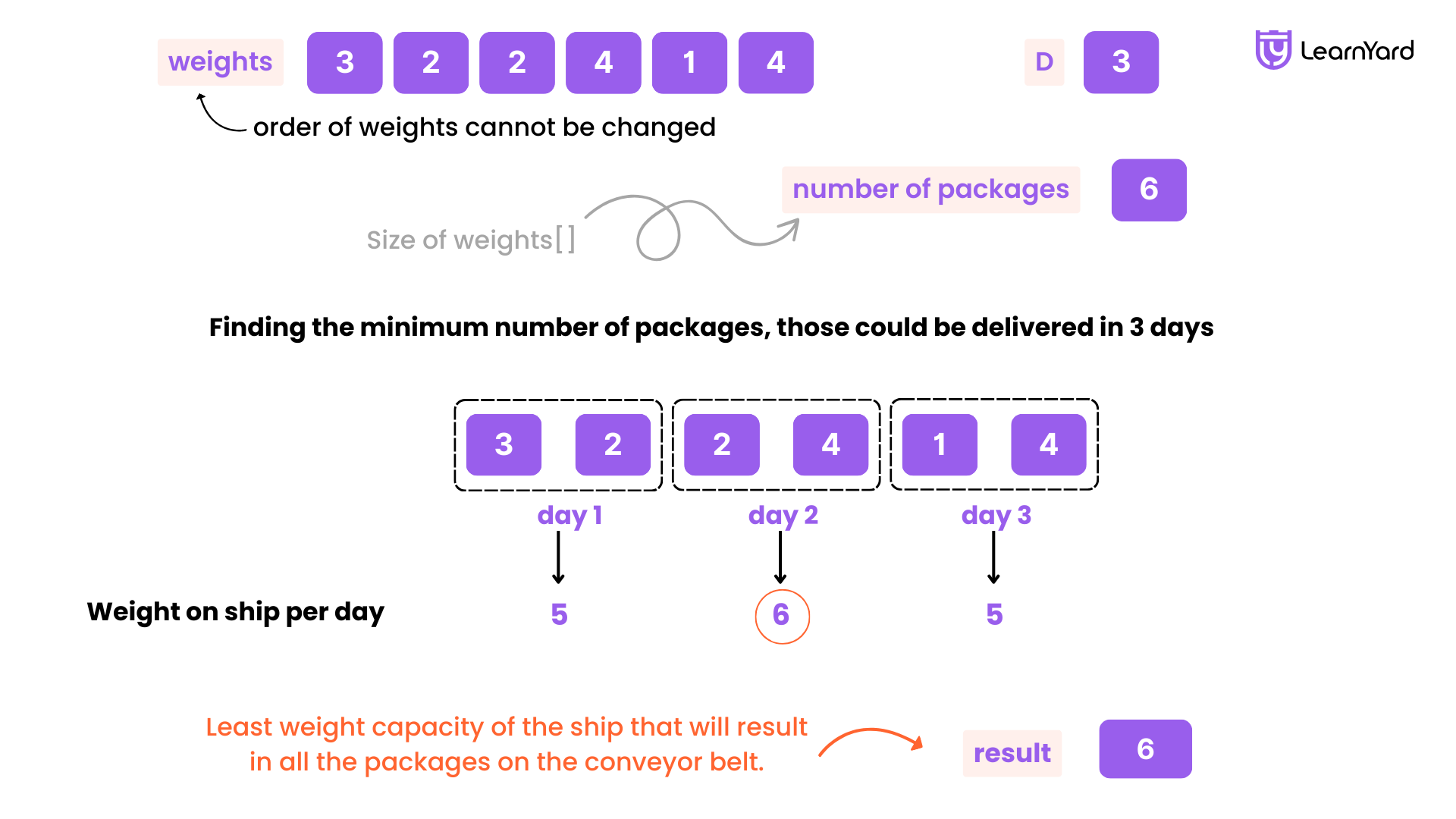
Input: weights = [3,2,2,4,1,4], D = 3
Output: 6
Explanation: A ship capacity of 6 is the minimum to ship all the packages in 3 days like this:
1st day: 3, 2
2nd day: 2, 4
3rd day: 1, 4
Input: weights = [1,2,3,1,1], D = 4
Output: 3
Explanation:
1st day: 1
2nd day: 2
3rd day: 3
4th day: 1, 1
Constraints:
1 <= D <= weights.length <= 5 * 10⁴
1 <= weights[i] <= 500
Brute Force Approach
To approach the problem, we are given some packages with their weights and an integer D, and we need to ship these packages from one port to another within D days.
Our goal is to find the minimum weight capacity of the ship such that it can carry packages daily and complete the task within the given days. Let’s think through this step by step.
First, what can be the minimum weight capacity of the ship?
The minimum weight capacity of the ship should be equal to the weight of the heaviest package. This is because if the minimum capacity of the ship is less than the weight of the heaviest package, we would never be able to transport that package. For example, if the heaviest package weighs 10, the minimum weight capacity of the ship should be at least 10 to carry this package.
Now that we know the minimum weight capacity, what would be the maximum weight capacity the ship can have?
While the maximum capacity can theoretically be very large, a practical and relevant maximum capacity is the total sum of the weights of all packages. This would allow the ship to transport all the packages in one day.
Now we have both the minimum and maximum weight capacities the ship can have. The problem boils down to finding the minimum capacity that allows the ship to transport all packages within D days.
One basic approach is to start checking from the minimum capacity and calculate how many days it would take to ship all the packages with that capacity. If it takes less than or equal to D days, then it’s a valid solution; otherwise, we increase the capacity and check again. We continue this process until we reach the maximum weight capacity.
Since the range from minimum to maximum covers all possible weight capacities a ship can have, starting from the minimum and stopping at the capacity where it takes less than or equal to D days will give us the desired result.
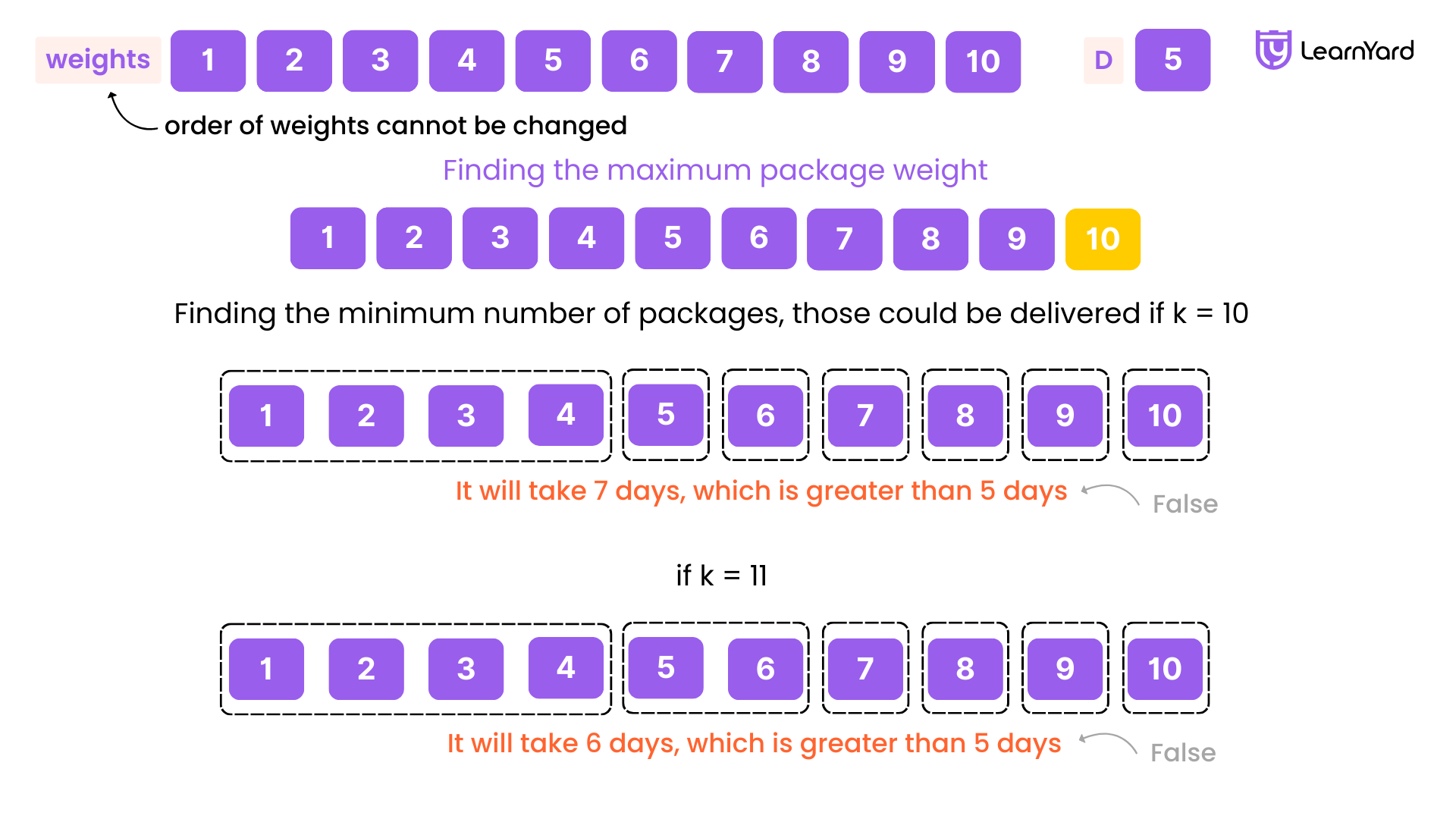
Consider the example with weights [1, 2, 3, 4, 5, 6, 7, 8, 9, 10] and D = 5.
We start by taking the maximum package weight, which is 10, as the minimum possible weight capacity for the ship. We then check how many days it will take to ship all the packages with this capacity:
- For a capacity of 10, it will take 7 days, which is more than 5 days, so it doesn't work.
- For 11, it will take 6 days, still more than 5 days, so it doesn't work.
- For 12, 13, and 14, it will still take 6 days, which is more than 5 days, so they don't work either.
- But for 15, it takes exactly 5 days, which is the allowed number of days, so it works.
- For 16 or any capacity greater than 15, it will take 5 days or fewer, so they all work.
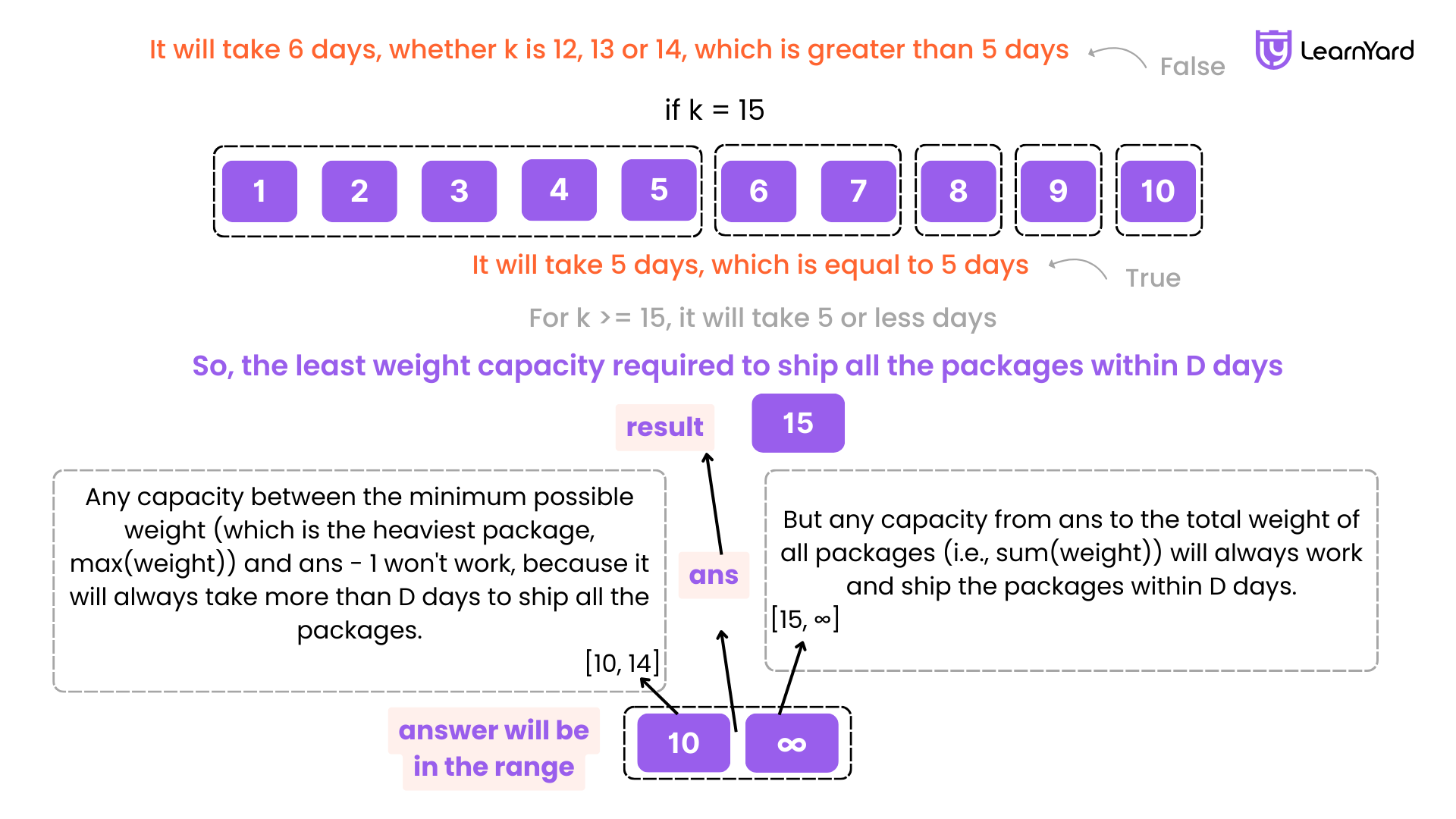
This shows that 15 is the smallest capacity that satisfies the condition (i.e., all packages can be shipped within 5 days). Any capacity greater than 15 will also work, but any capacity smaller than 15 will not meet the condition. Therefore, 15 is the least weight capacity required to ship all the packages within D days.
So, the answer is 15.
Let's call the smallest weight capacity needed to ship all the packages within D days as ans.
- Any capacity between the minimum possible weight (which is the heaviest package, max(weight)) and ans - 1 won't work, because it will always take more than D days to ship all the packages.
- But any capacity from ans to the total weight of all packages (i.e., sum(weight)) will always work and ship the packages within D days.
Therefore, ans is the smallest weight capacity that allows the ship to deliver all packages in D days. We will return ans as the least weight capacity needed to ship all the packages on time.
How can we determine the number of days required for a ship to transport all packages given its weight capacity?
Imagine you have a ship that can carry a certain amount of weight each day, and you need to ship a series of packages. The ship can only carry the packages in the order they're given.
To figure out how many days it will take, we start by counting the days. Initially, we assume it will take at least 1 day, so we set dayCount to 1. We also keep track of how much weight is currently on the ship with a variable called currentLoad.
Now, we go through each package one by one. If adding a package to the ship’s current load doesn’t exceed the ship’s weight capacity, we just add it to currentLoad and keep moving forward.
But, if adding a package makes the ship’s load exceed its capacity, we know the ship can't carry it today. So, we count that as a new day (dayCount++), and we reset currentLoad to 0, because the ship starts fresh the next day. Then, we add that package to the load, and the process continues until all packages are delivered.
In the end, the dayCount will tell us how many days it will take to ship all the packages with the given weight capacity of the ship.
How to do it?
- First, we calculate the minimum possible capacity as the weight of the heaviest package, since the ship must at least be able to carry the heaviest package.
- Next, we calculate the maximum possible capacity as the sum of the weights of all packages, as this would allow all packages to be transported in a single day.
- Then, we start iterating from the minimum possible capacity and check how many days it would take to transport all the packages with this capacity.
- If the number of days required is less than or equal to the given D, we return this capacity as it satisfies the condition.
- Otherwise, we increase the capacity and repeat the process until we find the minimum capacity that works.
Let's understand with an example:
Input: weights = [1,2,3,4,5,6,7,8,9,10], D = 5
- Calculate minimum and maximum capacity:
Minimum capacity = max(weights) = 10 (heaviest package).
Maximum capacity = sum(weights) = 55 (sum of all packages). - Iterate from minimum to maximum capacity:
Start with capacity = 10 and check how many days it takes:
Day 1: [1, 2, 3, 4] (total 10),
Day 2: [5] (total 5),
Day 3: [6] (total 6),
Day 4: [7] (total 7),
Day 5: [8] (total 8),
Day 6: [9] (total 9),
Day 7: [10] (total 10).
Total days = 7 → Not valid.
Increase capacity and repeat the process until it satisfies the condition. - Similarly, for capacities 11, 12, 13, and 14, the total days required to ship all the packages will still be greater than 5, as the ship cannot carry enough packages per day to meet the given time constraint.
- Continue until capacity = 15:
Capacity = 15, check days:
Day 1: [1, 2, 3, 4, 5] (total 15),
Day 2: [6, 7] (total 13),
Day 3: [8] (total 8),
Day 4: [9] (total 9),
Day 5: [10] (total 10).
Total days = 5 → Valid. - Return capacity = 15.
This is the minimum capacity that works, so the result is 15.
Steps to Implement the Solution:
- Initialize Variables:
Find the maximum weight (heaviest package) as the minimum possible capacity.
Calculate the total weight (sum of all package weights) as the maximum possible capacity. - Iterate Over Capacities:
Start iterating from the minimum capacity (maximum weight) to the maximum capacity (total weight). - Simulate Shipping Days for Each Capacity:
Initialize day count to 1 and current load to 0.
For each package weight:
If adding the current package exceeds the current capacity, increment the day count and reset the current load.
Add the current package weight to the current load. - Check Validity of Capacity:
If the total day count is less than or equal to the given number of days, return the current capacity. - Fallback Return:
Return the maximum capacity as the default, though this case shouldn't occur if the input is valid.
Code Implementation / LeetCode Solutions for "Capacity To Ship Packages Within D Days"
1. C++ Try on Compiler
class Solution {
public:
int shipWithinDays(vector<int>& weights, int days) {
// Find the heaviest package as the minimum possible capacity
int maxWeight = *max_element(weights.begin(), weights.end());
// Find the sum of all package weights as the maximum possible capacity
int totalWeight = accumulate(weights.begin(), weights.end(), 0);
// Iterate from minimum capacity to maximum capacity
for (int capacity = maxWeight; capacity <= totalWeight; capacity++) {
// Start with 1 day
int dayCount = 1;
// Track the current load on the ship
int currentLoad = 0;
// Loop through each package weight
for (int weight : weights) {
// If the current load exceeds capacity, start a new day
if (currentLoad + weight > capacity) {
dayCount++;
currentLoad = 0;
}
// Add the current package weight to the load
currentLoad += weight;
}
// If the number of days is within the allowed limit, return capacity
if (dayCount <= days) {
return capacity;
}
}
// Fallback return, though it won't be reached in valid cases
return totalWeight;
}
};2. Java Try on Compiler
class Solution {
public int shipWithinDays(int[] weights, int days) {
// Find the heaviest package as the minimum possible capacity
int maxWeight = Arrays.stream(weights).max().getAsInt();
// Find the sum of all package weights as the maximum possible capacity
int totalWeight = Arrays.stream(weights).sum();
// Iterate from minimum capacity to maximum capacity
for (int capacity = maxWeight; capacity <= totalWeight; capacity++) {
// Start with 1 day
int dayCount = 1;
// Track the current load on the ship
int currentLoad = 0;
// Loop through each package weight
for (int weight : weights) {
// If the current load exceeds capacity, start a new day
if (currentLoad + weight > capacity) {
dayCount++;
currentLoad = 0;
}
// Add the current package weight to the load
currentLoad += weight;
}
// If the number of days is within the allowed limit, return capacity
if (dayCount <= days) {
return capacity;
}
}
// Fallback return, though it won't be reached in valid cases
return totalWeight;
}
}
3. Python Try on Compiler
class Solution:
def shipWithinDays(self, weights, days):
# Find the heaviest package as the minimum possible capacity
max_weight = max(weights)
# Find the sum of all package weights as the maximum possible capacity
total_weight = sum(weights)
# Iterate from minimum capacity to maximum capacity
for capacity in range(max_weight, total_weight + 1):
# Start with 1 day
day_count = 1
# Track the current load on the ship
current_load = 0
# Loop through each package weight
for weight in weights:
# If the current load exceeds capacity, start a new day
if current_load + weight > capacity:
day_count += 1
current_load = 0
# Add the current package weight to the load
current_load += weight
# If the number of days is within the allowed limit, return capacity
if day_count <= days:
return capacity
# Fallback return, though it won't be reached in valid cases
return total_weight
4. Javascript Try on Compiler
/**
* @param {number[]} weights
* @param {number} days
* @return {number}
*/
var shipWithinDays = function (weights, days) {
// Find the heaviest package as the minimum possible capacity
const maxWeight = Math.max(...weights);
// Find the sum of all package weights as the maximum possible capacity
const totalWeight = weights.reduce((sum, weight) => sum + weight, 0);
// Iterate from minimum capacity to maximum capacity
for (let capacity = maxWeight; capacity <= totalWeight; capacity++) {
// Start with 1 day
let dayCount = 1;
// Track the current load on the ship
let currentLoad = 0;
// Loop through each package weight
for (let weight of weights) {
// If the current load exceeds capacity, start a new day
if (currentLoad + weight > capacity) {
dayCount++;
currentLoad = 0;
}
// Add the current package weight to the load
currentLoad += weight;
}
// If the number of days is within the allowed limit, return capacity
if (dayCount <= days) {
return capacity;
}
}
// Fallback return, though it won't be reached in valid cases
return totalWeight;
};Time Complexity: O(n * (totalWeight - maxWeight))
- Finding the Maximum Weight (maxWeight)
This is done using max_element in C++ (or equivalent in other languages), which takes O(n) time, where n is the number of packages (i.e., the length of the weights array). - Finding the Total Weight (totalWeight)
This is done using accumulate in C++ (or equivalent in other languages), which also takes O(n) time, as it sums up all the weights in the array. - Iterating Over Possible Capacities
The outer loop iterates from maxWeight to totalWeight, i.e., it runs for (totalWeight - maxWeight + 1) iterations.
In the worst case, this will be O(totalWeight) iterations, which is roughly O(totalWeight) since the maxWeight is generally much smaller than totalWeight. - Iterating Over the Weights for Each Capacity
For each capacity, we check how many days are needed to ship all the packages. This involves iterating over all the package weights, which takes O(n) time for each capacity. - Combining All the Steps
We have an outer loop iterating up to O(totalWeight) times and an inner loop iterating O(n) times for each capacity. Thus, the overall time complexity of the solution is O(n * (totalWeight - maxWeight)).
Where:
n is the number of packages.
totalWeight is the sum of all package weights (which could be as large as the sum of all weights in the worst case).
maxWeight is the maximum package weight.
Space Complexity: O(n)
- Auxiliary Space Complexity: O(1)
The extra space used for variables like maxWeight, totalWeight, currentLoad, and dayCount is constant. These are just primitive variables that occupy O(1) space.
Therefore, the auxiliary space complexity is O(1). - Total Space Complexity: O(n)
The weights array, which holds the input values, occupies O(n) space, where n is the number of packages (elements in the array).
There is no additional space for data structures like lists, arrays, or hash maps apart from the input array itself.
Therefore, the total space complexity is O(n).
Will Brute Force Work Against the Given Constraints?
For the current solution, the time complexity is O(n * (totalWeight - maxWeight)), which is not reasonable given the problem constraints. Here, n is the number of packages (with an upper limit of 5 * 10⁴), and totalWeight is the sum of all package weights, which can be as large as 500 * 5 * 10⁴ = 2.5 * 10⁷ in the worst-case scenario. This means the solution can handle up to approximately O(2.5 * 10⁷) operations in the worst case.
However, since the constraints allow up to 5 * 10⁴ packages, the solution is not efficient enough for many typical inputs. In competitive programming environments, problems generally allow up to 10⁶ operations per test case. While the time complexity may exceed this for the worst-case scenario, most inputs will likely stay within a manageable range and execute efficiently within the given time limits.
Therefore, the O(n * totalWeight) time complexity does not ensure that the solution works efficiently for a wide range of inputs within the problem's constraints. While it may perform well for typical inputs, it is important to consider the worst-case inputs that could push the solution beyond the upper limit. With careful optimization, it could perform well in most practical cases.
How to optimize it?
In the previous approach, we looked at the minimum and maximum weight capacities of the ship and checked every capacity in that range to find the smallest one that could transport all packages in the given number of days. This gave us O(n * (totalWeight - maxWeight)) time complexity, which was too slow and caused TLE (Time Limit Exceeded).
Now, let’s think about improving this.
The main issue was that we checked every capacity from minimum to maximum, which took a lot of time.
Can we make this part faster?
Yes! Here’s the hint:
We are searching for the minimum capacity that works, and we know it lies between the minimum weight capacity (the heaviest package) and the maximum weight capacity (sum of all package weights).
Now that we know the two endpoints, the minimum weight capacity and the maximum weight capacity, let's make a few observations:
- The data structure is sorted:
The range of capacities, from the minimum to the maximum, is naturally sorted. - The search space is monotonic:
- If a certain capacity can ship all packages within the required days, then any larger capacity will also work.
- If a certain capacity cannot ship all packages, then any smaller capacity will also fail.
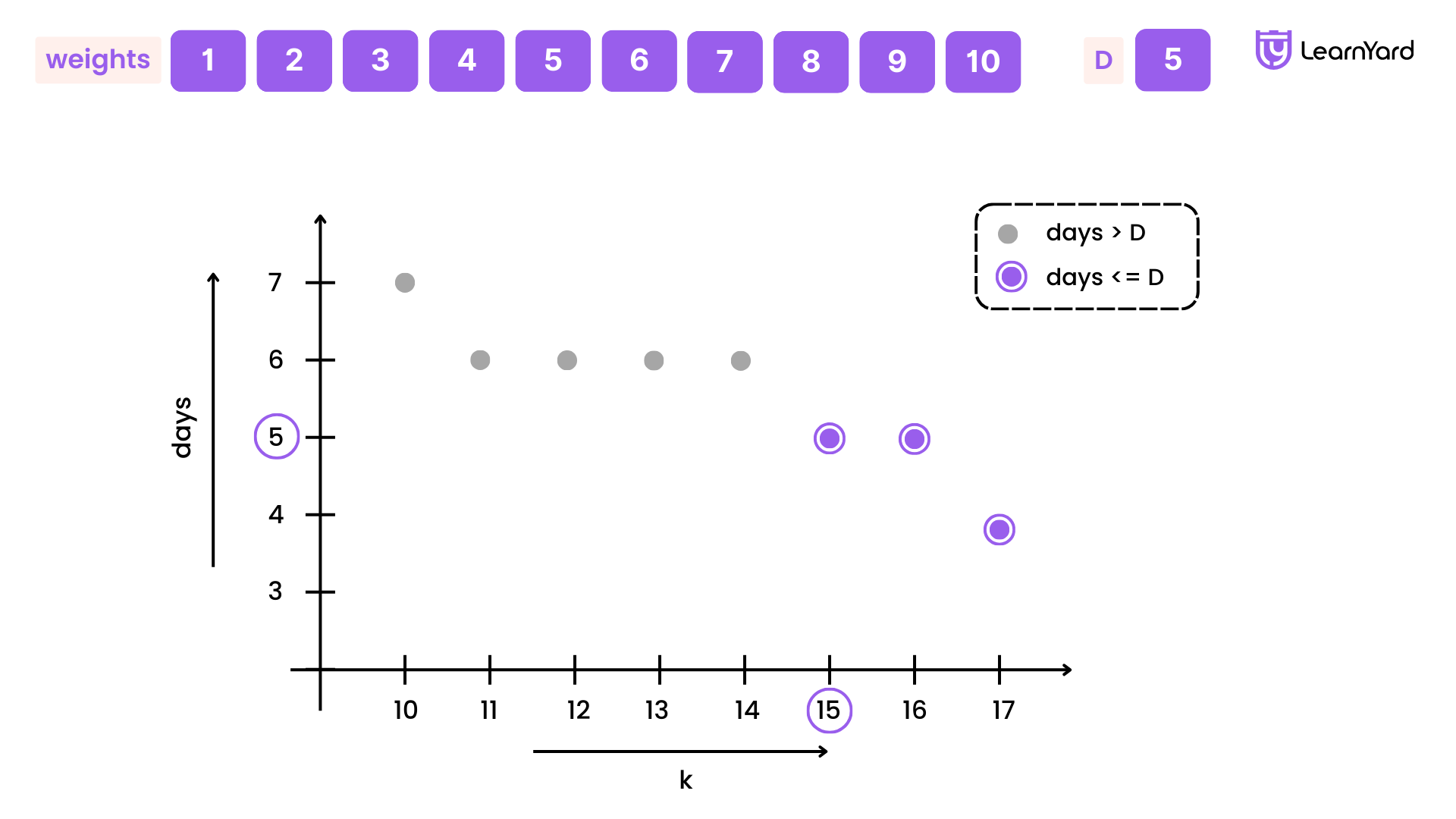
- For the example with the package weights [1, 2, 3, 4, 5, 6, 7, 8, 9, 10] and days = 5, the ship will fail to deliver within 5 days for all capacities from 1 to 14 (F, F, F, F... up to 14). Starting from capacity 15 onwards, the ship will succeed in delivering the packages within the required 5 days (T, T, T, T...). This illustrates the monotonic property: once the capacity works (from 15), it will continue to work for all larger capacities.
- The middle element helps minimize or maximize the search space:
If we take the middle value of the current range and check if it works (i.e., can ship all packages within the given number of days), we can narrow the search space:- If it works, we move to the left half to find a smaller valid capacity.
- If it doesn’t work, we move to the right half to find a larger capacity that works.
If we plot a graph with the weight capacity of the ship on the x-axis and the number of days required to ship all the packages on the y-axis, we can observe the following:
For a given weight capacity, we can either ship the packages within the allowed days or not. Before reaching the minimum capacity (denoted as minCapacity), it is impossible to ship all the packages within the given days. This is because, for any capacity lower than minCapacity, the ship would require more days than allowed to transport the packages. Once we reach minCapacity, it becomes possible to ship all the packages within the required number of days. This condition remains valid for all capacities greater than or equal to minCapacity. The ship can now carry the packages within the required days, and this will continue to be true as we increase the capacity further.
Thus, minCapacity represents the minimum weight capacity at which the ship can start shipping all the packages within the given days, and from that point forward, increasing the capacity will always allow the ship to ship the packages within the allowed days.
With these points in mind, it's clear that instead of linearly checking all values from the minimum to the maximum capacity, we can take the middle value and continually reduce the search space.
Does this approach remind you of something you've seen before?
Yes, we are applying binary search here. By leveraging the sorted and monotonic properties of the capacity range, we efficiently narrow down the search space to find the minimum capacity that meets the condition, instead of checking each value linearly.
Binary search can help us quickly find this capacity by narrowing down the range in each step.
We can simply use binary search to determine the minimum weight capacity of the ship needed to transport all packages in D days.
Start by taking the middle value between low (minimum weight capacity) and high (maximum weight capacity). If this mid-value satisfies the condition that the number of days required is less than or equal to D, we store it as a potential answer and narrow the search space to the left half, looking for a smaller capacity. Otherwise, we move the search to the right half to find a larger valid capacity. We continue this process as long as low <= high.
Once the condition breaks, the stored answer is returned as the minimum capacity.
By using binary search, we can cut the search space in half at each step, which makes the solution much faster and avoids the TLE issue.
How to do it?
- First, we calculate the minimum possible capacity as the weight of the heaviest package since the ship must at least be able to carry the heaviest package.
- Next, we calculate the maximum possible capacity as the sum of the weights of all packages, as this would allow all packages to be transported in a single day.
- Then, we use binary search between the minimum and maximum capacity to find the smallest capacity that works.
- In each step, we calculate the mid-point of the current range and check how many days it would take to transport all packages with this capacity.
- If the number of days required is less than or equal to the given days, we move to the left half to find a smaller valid capacity.
- Otherwise, we move to the right half to try larger capacities.
We repeat this process until we find the minimum capacity that satisfies the condition.
Let's understand with an example:
Input: weights = [1,2,3,4,5,6,7,8,9,10], D = 5
Binary Search Dry Run:
- Initial Range:
Minimum Capacity = max(weights) = 10 (heaviest package).
Maximum Capacity = sum(weights) = 55 (all packages in one day). - Step 1:
- Mid = (10 + 55) // 2 = 32.
- Check with capacity = 32:
- Day 1: [1,2,3,4,5,6,7] (28).
- Day 2: [8,9,10] (27).
- Total Days = 2 ≤ 5 → Valid.
- Update range: [10, 31].
- Step 2:
- Mid = (10 + 31) // 2 = 20.
- Check with capacity = 20:
- Day 1: [1,2,3,4,5] (15).
- Day 2: [6,7] (13).
- Day 3: [8,9] (17).
- Day 4: [10] (10).
- Total Days = 4 ≤ 5 → Valid.
- Update range: [10, 19].
- Step 3:
- Mid = (10 + 19) // 2 = 14.
- Check with capacity = 14:
- Day 1: [1,2,3,4] (10).
- Day 2: [5,6] (11).
- Day 3: [7] (7).
- Day 4: [8] (8).
- Day 5: [9] (9).
- Day 6: [10] (10).
- Total Days = 6 > 5 → Invalid.
- Update range: [15, 19].
- Step 4:
- Mid = (15 + 19) // 2 = 17.
- Check with capacity = 17:
- Day 1: [1,2,3,4,5] (15).
- Day 2: [6,7] (13).
- Day 3: [8,9] (17).
- Day 4: [10] (10).
- Total Days = 4 ≤ 5 → Valid.
- Update range: [15, 16].
- Step 5:
- Mid = (15 + 16) // 2 = 15.
- Check with capacity = 15:
- Day 1: [1,2,3,4,5] (15).
- Day 2: [6,7] (13).
- Day 3: [8] (8).
- Day 4: [9] (9).
- Day 5: [10] (10).
- Total Days = 5 → Valid.
- Update range: [15, 14].
Result: Minimum capacity = 15.
Optimal Animation Explaination
How to code it up:
Here are concise steps to code up the solution generically:
- Define the Binary Search Range:
Initialize low as the weight of the heaviest package (minimum capacity).
Initialize high as the total weight of all packages (maximum capacity). - Helper Function for Validation:
Write a function to check if a given capacity can transport all packages within the given days.
Simulate the process: iterate through the packages, keeping track of the current load and counting the days.
If the load exceeds the capacity, start a new day. - Binary Search Logic:
Perform binary search within the range of capacities (low to high).
Calculate the mid-point capacity.
Use the helper function to check if the mid-point capacity is valid:
If valid, update the answer to mid and narrow the search to the lower half (high = mid - 1).
Otherwise, search the upper half (low = mid + 1). - Return the Result:
Once the binary search ends, return the last valid capacity as the minimum required capacity.
Code Implementation / LeetCode Solutions for "Capacity To Ship Packages Within D Days"
1. C++ Try on Compiler
class Solution {
// Helper function to check if the given capacity can ship all packages in the given days
bool check(int mid, vector<int>& weights, int days)
{
// Start with 1 day
int count = 1;
// Current load of the ship
int limit = 0;
// Iterate through the weights
for(auto &weight: weights)
{
// If adding the current weight doesn't exceed the capacity, add it to the current load
if(limit + weight <= mid)
{
limit += weight;
}
else
{
// If it exceeds, start a new day and reset the current load
limit = 0;
limit += weight;
count++;
}
}
// Return true if the number of days required is within the given days
return count <= days;
}
public:
int shipWithinDays(vector<int>& weights, int days) {
// Find the minimum possible capacity (heaviest package)
int low = *max_element(weights.begin(), weights.end());
// Find the maximum possible capacity (sum of all weights)
int high = accumulate(weights.begin(), weights.end(), 0);
int ans = 0; // Variable to store the result
// Perform binary search to find the minimum capacity
while(low <= high)
{
int mid = (low + high)/2; // Calculate the middle capacity
// Check if the mid capacity is valid
if(check(mid, weights, days))
{
ans = mid; // Update the result
high = mid-1; // Search in the lower half
}
else
low = mid+1; // Search in the upper half
}
// Return the minimum capacity required
return ans;
}
};
2. Java Try on Compiler
class Solution {
// Helper function to check if the given capacity can ship all packages in the given days
private boolean check(int mid, int[] weights, int days) {
int count = 1; // Start with 1 day
int limit = 0;
// Current load of the ship
for (int weight : weights) {
// If adding the current weight doesn't exceed the capacity, add it to the current load
if (limit + weight <= mid) {
limit += weight;
} else {
// If it exceeds, start a new day and reset the current load
limit = weight;
count++;
}
}
// Return true if the number of days required is within the given days
return count <= days;
}
public int shipWithinDays(int[] weights, int days) {
// Find the minimum possible capacity (heaviest package)
int low = Integer.MIN_VALUE;
for (int weight : weights) {
low = Math.max(low, weight);
}
// Find the maximum possible capacity (sum of all weights)
int high = 0;
for (int weight : weights) {
high += weight;
}
int ans = 0; // Variable to store the result
// Perform binary search to find the minimum capacity
while (low <= high) {
int mid = low + (high - low) / 2; // Calculate the middle capacity
// Check if the mid capacity is valid
if (check(mid, weights, days)) {
ans = mid; // Update the result
high = mid - 1; // Search in the lower half
} else {
low = mid + 1; // Search in the upper half
}
}
// Return the minimum capacity required
return ans;
}
}
3. Python Try on Compiler
class Solution:
# Helper function to check if the given capacity can ship all packages in the given days
def check(self, mid, weights, days):
count = 1 # Start with 1 day
limit = 0 # Current load of the ship
# Iterate through the weights
for weight in weights:
# If adding the current weight doesn't exceed the capacity, add it to the current load
if limit + weight <= mid:
limit += weight
else:
# If it exceeds, start a new day and reset the current load
limit = weight
count += 1
# Return true if the number of days required is within the given days
return count <= days
def shipWithinDays(self, weights, days):
# Find the minimum possible capacity (heaviest package)
low = max(weights)
# Find the maximum possible capacity (sum of all weights)
high = sum(weights)
ans = 0 # Variable to store the result
# Perform binary search to find the minimum capacity
while low <= high:
mid = (low + high) // 2 # Calculate the middle capacity
# Check if the mid capacity is valid
if self.check(mid, weights, days):
ans = mid # Update the result
high = mid - 1 # Search in the lower half
else:
low = mid + 1 # Search in the upper half
# Return the minimum capacity required
return ans
4. Javascript Try on Compiler
/**
* @param {number[]} weights
* @param {number} days
* @return {number}
*/
// Helper function to check if the given capacity can ship all packages in the given days
var check = function(mid, weights, days) {
let count = 1; // Start with 1 day
let limit = 0; // Current load of the ship
// Iterate through the weights
for (let weight of weights) {
// If adding the current weight doesn't exceed the capacity, add it to the current load
if (limit + weight <= mid) {
limit += weight;
} else {
// If it exceeds, start a new day and reset the current load
limit = weight;
count++;
}
}
// Return true if the number of days required is within the given days
return count <= days;
};
var shipWithinDays = function (weights, days) {
// Find the minimum possible capacity (heaviest package)
let low = Math.max(...weights);
// Find the maximum possible capacity (sum of all weights)
let high = weights.reduce((sum, weight) => sum + weight, 0);
let ans = 0; // Variable to store the result
// Perform binary search to find the minimum capacity
while (low <= high) {
let mid = Math.floor((low + high) / 2); // Calculate the middle capacity
// Check if the mid capacity is valid
if (check(mid, weights, days)) {
ans = mid; // Update the result
high = mid - 1; // Search in the lower half
} else {
low = mid + 1; // Search in the upper half
}
}
// Return the minimum capacity required
return ans;
};Time Complexity: O(n * log(sum(weights) - max(weights)))
Binary Search Loop:
The binary search operates between low and high.
The initial range is between:
low = max(weights) (the heaviest package).
high = sum(weights) (the sum of all weights).
The binary search loop runs for log(range) iterations, where range = sum(weights) - max(weights). This means that the binary search loop will run O(log(sum(weights) - max(weights))) times.
Check Function:
The check function is called during each binary search iteration.
Inside the check function, we iterate over all the weights, which takes O(n) time, where n is the number of packages.
Total Time Complexity:
The overall time complexity is the product of the number of binary search iterations and the complexity of the check function:
Binary search iterations: O(log(sum(weights) - max(weights)))
Check function: O(n)
Therefore, the total time complexity is: O(n * log(sum(weights) - max(weights)))
Where:
n is the number of packages.
sum(weights) is the sum of all package weights.
max(weights) is the maximum package weight.
Space Complexity: O(n)
- Auxiliary Space Complexity: O(1)
The space complexity is O(1) because we only use a constant amount of extra space (apart from the input data). - Total Space Complexity: O(n)
The total space complexity is O(n) because we store the input weights array.
Therefore, the total space complexity is O(n).
Learning Tip
Now we have successfully tackled this problem, let's try these similar problems.
A conveyor belt has packages that must be shipped from one port to another within D days.The ith package on the conveyor belt has a weight of weights[i]. Each day, we load the ship with packages on the conveyor belt (in the order given by weights). We may not load more weight than the maximum weight capacity of the ship.Return the least weight capacity of the ship that will result in all the packages on the conveyor belt being shipped within D days.
2. Sqrt(x)
Given a non-negative integer x, return the square root of x rounded down to the nearest integer. The returned integer should be non-negative as well.You must not use any built-in exponent function or operator.For example, do not use pow(x, 0.5) in C++ or x ** 0.5 in Python.