Boats to Save People Solution In C++/Java/Python/JS
Problem Description
You are given an array people where people[i] is the weight of the ith person, and an infinite number of boats where each boat can carry a maximum weight of limit. Each boat carries at most two people at the same time, provided the sum of the weight of those people is at most limit.
Return the minimum number of boats to carry every given person.
Examples
Input: people = [1,2], limit = 3
Output: 1
Explanation: 1 boat (1, 2)
Input: people = [3,2,2,1], limit = 3
Output: 3
Explanation: 3 boats (1, 2), (2) and (3)
Constraints
- 1 <= people.length <= 5 * 104
- 1 <= people[i] <= limit <= 3 * 104
The first thing we need to figure out is how to use the least number of boats without going over the weight limit. One smart way is to sort everyone by weight and always try to pair the lightest person with the heaviest one. If they fit together, great — we send them in one boat. If not, the heavier one goes alone. We keep repeating this process until everyone is placed. This simple greedy idea helps us make the most out of each boat and works well even when the input size is large.
Greedy Approach
Intuition
We’re given people with different weights and a limit on how much a boat can carry. Each boat can carry at most two people, but only if their total weight stays within the limit. The goal is to use the least number of boats to carry everyone.
Now before jumping into writing code, think of this like managing space wisely. If two people can share a boat, why send them separately? But obviously, we can’t just pair anyone randomly — we have to be smart about it. So we sort the people by their weights. This helps because we always know who’s the lightest and who’s the heaviest left.
Now the smart move: try to pair the lightest person with the heaviest one. If they fit within the weight limit, send them together. If they don’t, send the heavier person alone — because no one else can go with them anyway. We repeat this process, moving inward from both ends of the sorted list. Every time we do this, we’re making a greedy choice — the best move at that moment without looking too far ahead.
This simple strategy works well because it always tries to make full use of each boat. No extra checks, no wasting time on complex combinations. Just keep making the best move until all the people are on boats.
What is a Greedy Approach and Why It Works Here?
Greedy means we pick the best option available at each step, without thinking too far ahead. In this case, that means always trying to pair the lightest and heaviest person — it’s the most space-efficient move.
Why not try all combinations? Because we don’t need to. If the lightest and heaviest person can’t fit, then no one else can pair with the heaviest, so sending them alone is optimal.
By using two pointers — one from the start and one from the end — we process the list from both sides, pairing whenever possible. This helps us avoid wasting boats and gives us the minimum count in a clean and efficient way.
Example:
people = [1, 2, 2, 3], limit = 3
→ Sort: [1, 2, 2, 3]
→ 1 + 3 = 4 (too much) → send 3 alone
→ 1 + 2 = 3 (fits) → send together
→ send last 2 alone
Total boats = 3
To actually implement this idea, we start by sorting the array of weights. Then we use two pointers — one starting from the beginning (i, pointing to the lightest person) and one from the end (j, pointing to the heaviest). The idea is simple: check if people[i] + people[j] is within the limit. If it is, we move both pointers inward — they share a boat, so we do i++ and j--. But if they can’t fit together, the heavier person at j must go alone, so we just do j--. In both cases, we increase the boats count by 1. This loop continues until all people are placed and i crosses j.
The reason this greedy method works so well is because it always tries to make the most efficient use of the current boat. We never hold back or overthink — we just pick the best move available at that moment.By the end of this process, every person has either shared a boat with someone or gone alone — but always in the best way possible. That’s why this approach gives us the minimum number of boats needed.
Approach
Step 1: Sort the Array
We start by sorting the array of people by their weight.
This helps us efficiently match the lightest and heaviest unassigned individuals to try to fit them on the same boat.
Sorting ensures that we can make optimal pairing decisions as we scan from both ends.
Step 2: Use Two Pointers to Match People
We place two pointers:
- i: pointing to the lightest person (start of the array)
- j: pointing to the heaviest person (end of the array)
At each step: - If people[i] + people[j] ≤ limit, they can share a boat → move both pointers (i++, j--)
- If not, the heavier person must go alone → move only j--
Each iteration represents one boat being used.
Step 3: Continue Until All People Are Assigned
We repeat the process until i > j, meaning all people are placed into boats.
- This ensures everyone is accounted for with the minimum number of boats.
- People are processed exactly once, either paired or solo.
Step 4: Return the Total Boat Count
We maintain a counter to track the number of boats used throughout the process.
After all valid pairings are done, we return this counter as the final answer.
This method guarantees greedy pairing + minimal boat usage in a highly efficient way.
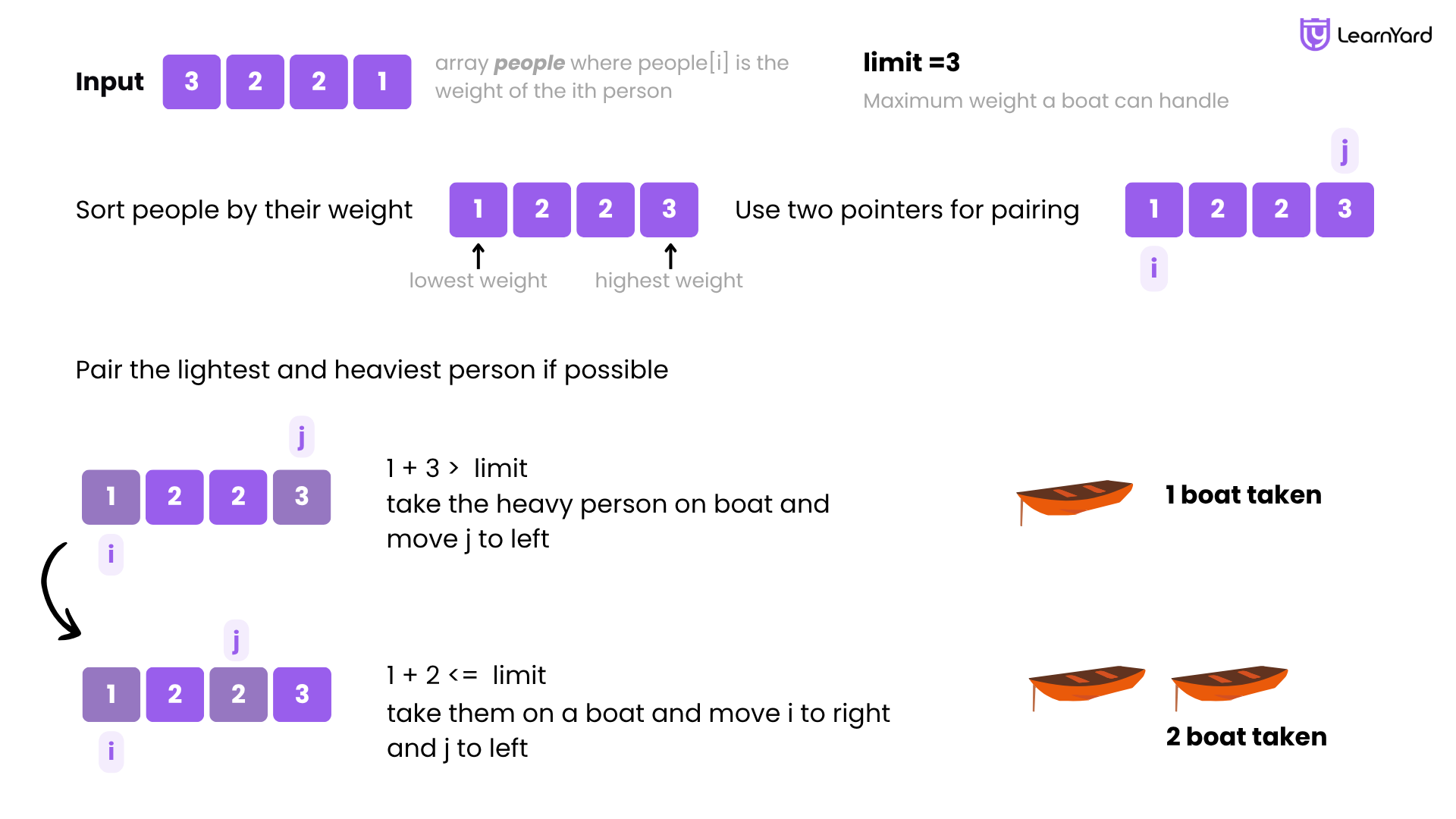
Dry Run
input : Input: people = [3, 2, 2, 1], limit = 3
Step 1: Sort the People Array
Sorted weights → people = [1, 2, 2, 3]
Initialize two pointers:
- i = 0 (lightest)
- j = 3 (heaviest)
- boats = 0
Iteration 1: i = 0, j = 3
- Try pairing: people[i] + people[j] = 1 + 3 = 4 → exceeds limit
- So, person j = 3 (weight 3) goes alone
- j-- → 2, boats = 1
Iteration 2: i = 0, j = 2
- Try pairing: 1 + 2 = 3 → within limit
- Pair them together
- i++ → 1, j-- → 1, boats = 2
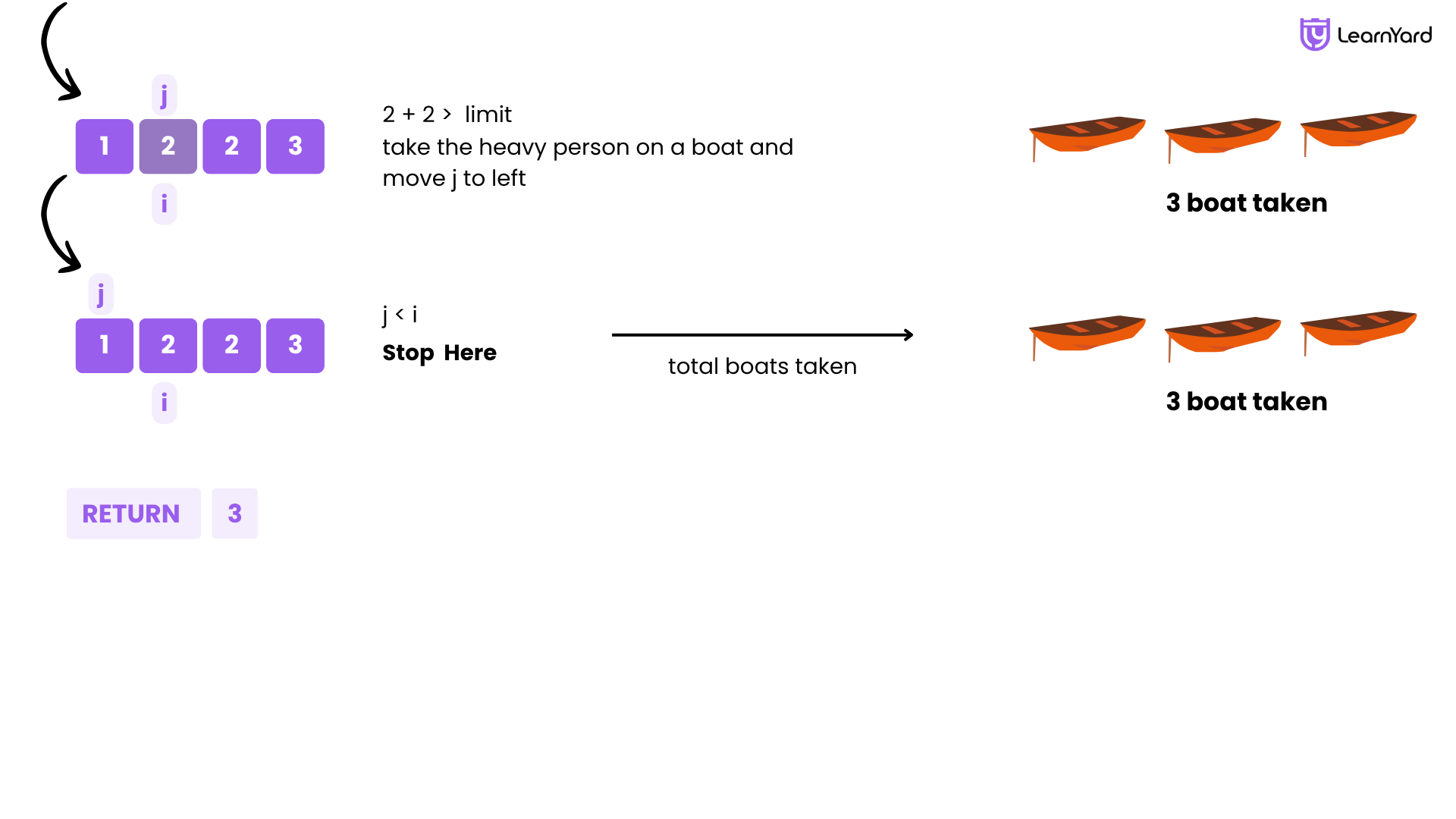
Iteration 3: i = 1, j = 1
- Only one person left: people[1] = 2
- Goes alone
- j-- → 0, boats = 3
Final Output:
- boats = 3
Code for All Languages
C++
#include <iostream> // For input and output
#include <vector> // For using vector
#include <algorithm> // For sort
using namespace std;
class Solution {
public:
int numRescueBoats(vector<int>& people, int limit) {
// Step 1: Sort people by their weight
sort(people.begin(), people.end());
// Step 2: Use two pointers for pairing
int i = 0; // Pointer to the lightest person
int j = people.size() - 1; // Pointer to the heaviest person
int boats = 0; // To count how many boats are used
// Step 3: Pair the lightest and heaviest person if possible
while (i <= j) {
// If their combined weight fits in one boat
if (people[i] + people[j] <= limit) {
i++; // Move to the next lightest person
}
// Always move the heaviest person (they take the boat)
j--;
// Use one boat in this step
boats++;
}
// Step 4: Return total boats used
return boats;
}
};
int main() {
int n, limit;
// Input number of people
cin >> n;
vector<int> people(n);
// Input weights of people
for (int i = 0; i < n; i++) {
cin >> people[i];
}
// Input weight limit of each boat
cin >> limit;
Solution sol;
int result = sol.numRescueBoats(people, limit);
// Output the minimum number of boats needed
cout << result << endl;
return 0;
}
Java
import java.util.*; // For Scanner and Arrays
class Solution {
public int numRescueBoats(int[] people, int limit) {
// Step 1: Sort the array to allow pairing from both ends
Arrays.sort(people);
// Step 2: Use two pointers
int i = 0; // Pointer to the lightest person
int j = people.length - 1; // Pointer to the heaviest person
int boats = 0; // To count number of boats used
// Step 3: Try pairing the heaviest with the lightest
while (i <= j) {
// If both can go together without exceeding the limit
if (people[i] + people[j] <= limit) {
i++; // Move to the next lightest person
}
// In any case, move the heaviest person (they take the boat)
j--;
// One boat is used in this step
boats++;
}
// Step 4: Return the total number of boats used
return boats;
}
}
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
// Input the number of people
int n = sc.nextInt();
int[] people = new int[n];
// Input the weights of people
for (int i = 0; i < n; i++) {
people[i] = sc.nextInt();
}
// Input the boat's weight limit
int limit = sc.nextInt();
Solution sol = new Solution();
int result = sol.numRescueBoats(people, limit);
// Output the result: minimum boats needed
System.out.println(result);
}
}
Python
# Approach: Optimal Greedy Two-Pointer Technique
# Language: Python
class Solution(object):
def numRescueBoats(self, people, limit):
"""
:type people: List[int]
:type limit: int
:rtype: int
"""
# Step 1: Sort the array to allow pairing from both ends
people.sort()
# Step 2: Use two pointers
i = 0 # Pointer to the lightest person
j = len(people) - 1 # Pointer to the heaviest person
boats = 0 # To count number of boats used
# Step 3: Pair the heaviest and lightest if possible
while i <= j:
# If both can go together without exceeding the limit
if people[i] + people[j] <= limit:
i += 1 # Move to the next lightest person
# Always move the heaviest person (they use the boat)
j -= 1
# One boat is used in this step
boats += 1
# Step 4: Return the total number of boats used
return boats
if __name__ == "__main__":
# Input the number of people
n = int(input())
# Input the weights of people
people = list(map(int, input().split()))
# Input the boat's weight limit
limit = int(input())
sol = Solution()
result = sol.numRescueBoats(people, limit)
# Output the result: minimum number of boats needed
print(result)
Javascript
// Approach: Optimal Greedy Two-Pointer Technique
// Language: JavaScript
/**
* @param {number[]} people - Array of people's weights
* @param {number} limit - Maximum weight limit per boat
* @return {number} - Minimum number of boats required
*/
var numRescueBoats = function(people, limit) {
// Step 1: Sort the array to allow pairing from both ends
people.sort((a, b) => a - b);
// Step 2: Initialize two pointers
let i = 0; // Pointer to the lightest person
let j = people.length - 1; // Pointer to the heaviest person
let boats = 0; // To count how many boats are used
// Step 3: Try to pair heaviest and lightest
while (i <= j) {
// If their combined weight fits the boat
if (people[i] + people[j] <= limit) {
i++; // Move to the next lightest person
}
// Always move the heaviest person (they take the boat)
j--;
// One boat is used in this step
boats++;
}
// Step 4: Return total number of boats used
return boats;
};
// Driver code to test in Node.js or browser console
(function () {
const readline = require("readline");
const rl = readline.createInterface({
input: process.stdin,
output: process.stdout
});
const inputLines = [];
rl.on("line", (line) => {
inputLines.push(line.trim());
if (inputLines.length === 3) {
rl.close();
}
});
rl.on("close", () => {
const n = parseInt(inputLines[0]); // Number of people
const people = inputLines[1].split(" ").map(Number); // People's weights
const limit = parseInt(inputLines[2]); // Boat limit
const result = numRescueBoats(people, limit);
console.log(result); // Output the result
});
})();
Time Complexity : O(n log n)
Sorting the Array — O(n log n)
We begin by sorting the people array to allow optimal pairing.
Let’s denote:
- n = number of elements in people
The sorting step takes O(n log n) time using any efficient built-in sort function.
Two-Pointer Traversal — O(n)
After sorting, we use two pointers:
- One from the start (lightest person)
- One from the end (heaviest person)
Each iteration of the loop processes one or two people.
Since each person is placed in a boat exactly once, the loop runs at most n times, contributing O(n) time overall.
Final Time Complexity: O(n log n)
- Sorting step → O(n log n)
- Pairing loop → O(n)
- Per-iteration work → O(1)
Since sorting dominates, the overall time complexity is: O(nlogn)
Space Complexity: O(1)
Auxiliary Space Complexity: O(1)
This refers to the extra memory used by the algorithm that is not part of the input or output.
In this greedy two-pointer approach, we use only a few integer variables:
- Two pointers (i and j)
- One boat counter (boats)
All of these occupy constant space, regardless of the input size.
We do not use any additional data structures like arrays, maps, or lists for computation.
Thus, the auxiliary space complexity is: O(n)
Total Space Complexity: O(n)
This includes:
Input Space:
- The input array people of length n → contributes O(n)
- Sorting is performed in place in most languages (like C++, Java, Python), so it doesn’t require extra array storage
Output Space:
- We return a single integer (number of boats), which is O(1)
- No result list or complex structure is constructed
Auxiliary Space:
- As discussed above, this is O(1)
So, the total space used by the algorithm is dominated by the input array: O(n)
Learning Tip
Now we have successfully tackled this problem, let’s try these similar problems.
There are n children standing in a line. Each child is assigned a rating value given in the integer array ratings.You are giving candies to these children subjected to the following requirements:Each child must have at least one candy.Children with a higher rating get more candies than their neighbors.Return the minimum number of candies you need to have to distribute the candies to the children.