Binary Subarrays With Sum Solutions in C++/Java/Python/JS
Problem Description
We are given a binary array nums containing only 0s and 1s) and an integer goal.
The task is to return the number of non-empty contiguous subarrays whose elements sum up exactly to goal.
What is a Subarray?
A subarray is a contiguous part of the array, meaning the elements are next to each other in the original array
Examples
- Original array: [1, 2, 3, 4]
Subarray: [2, 3]
Explanation: The numbers 2 and 3 appear side by side in the original array. - Original array: [9, 10, 11]
Subarray: [9, 10, 11]
Explanation: A subarray can be the entire array itself.
Examples
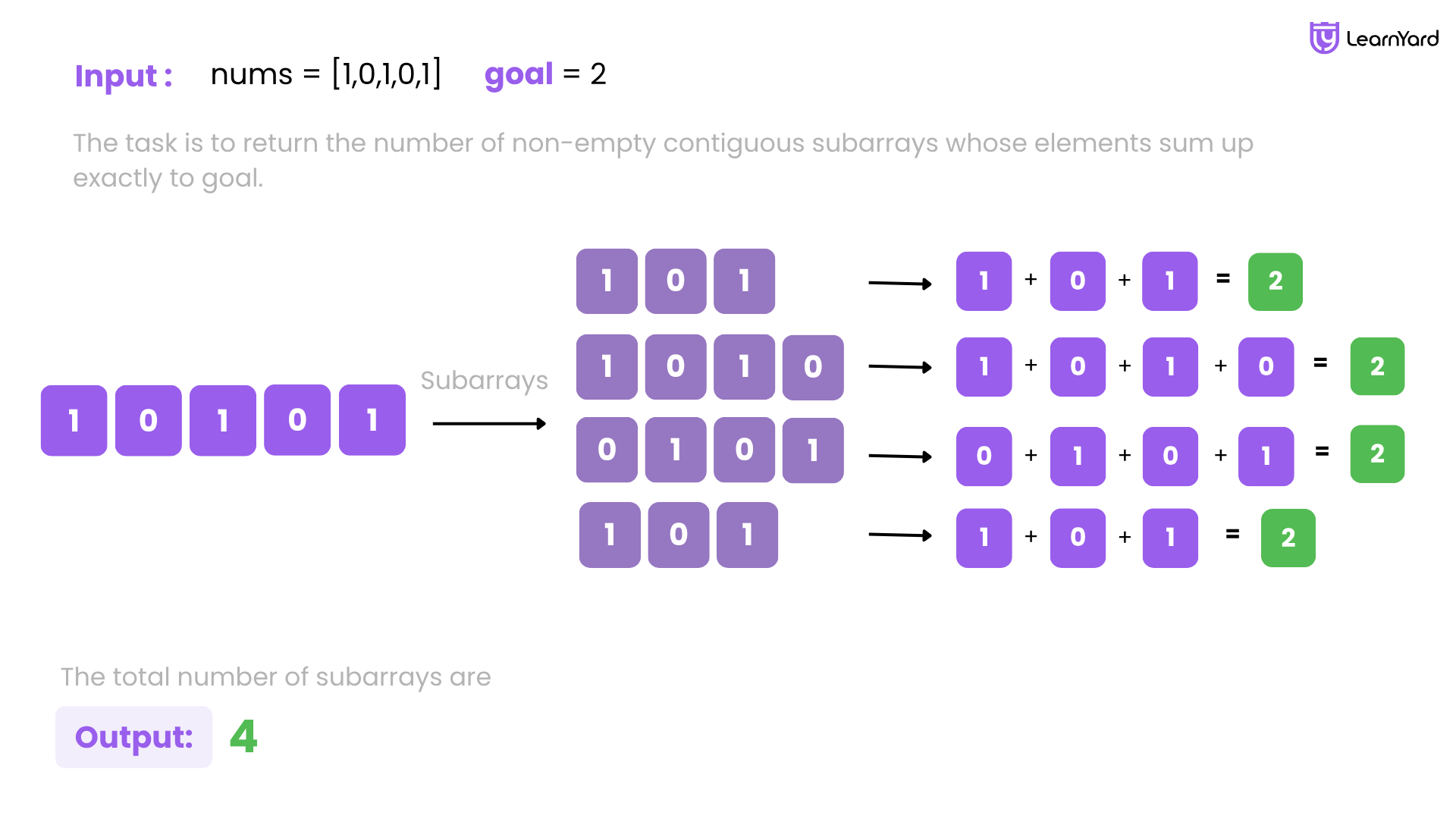
Input: nums = [1,0,1,0,1], goal = 2
Output: 4
Explanation: The 4 subarrays are bolded and underlined below:
[1,0,1,0,1]
[1,0,1,0,1]
[1,0,1,0,1]
[1,0,1,0,1]
Input: nums = [0,0,0,0,0], goal = 0
Output: 15
Constraints
- 1 <= nums.length <= 3 *10^4
- nums[i] is either 0 or 1
- 0 <= goal <= nums.length
When you first see this problem, the natural thought is: How do I count subarrays that add up to the goal? The most straightforward way? Just check every possible subarray, calculate its sum, and count the ones that match. This brute-force method is slow but easy to understand — and it helps build a strong foundation. Once we get that, we’ll move on to faster techniques like the sliding window and prefix sum with hashmap. Let’s start simple.
Brute Force Approach
Intuition
The first idea that comes to mind when solving this problem is pretty straightforward:
Check all possible subarrays of the array and count the ones that sum up to the target goal.
Since a subarray is just a contiguous segment of the array, we can use two nested loops — one to fix the starting index and one to expand to all valid endings.
Why Try All Subarrays?
There’s no shortcut in brute-force — we go one by one. We check every possible starting point and then explore every possible ending point from there. This way, we cover all non-empty subarrays, and for each, we calculate the sum. If it equals the goal, we count it. Yes, this takes time — but it’s clear, and it helps us understand the problem thoroughly before jumping into optimizations.
To make this happen, we’ll use nested loops — one to pick the starting point, and one to expand from that point and calculate the running sum.
Generating All Subarrays Using Nested Loops
To implement this, we first fix the starting index i of the subarray in nums using an outer loop. This loop runs from i = 0 up to i = nums.size(), ensuring that all possible subarrays are considered.
For each fixed starting index i, we use an inner loop with index j to build the subarray step by step. This inner loop runs from j = i to j < nums.size(). We maintain a variable current_sum and keep adding elements from nums[j] one by one. This helps us compute the sum of every possible subarray starting at index i without using extra space.
Each time the running sum becomes equal to the given goal, we increment a counter. This way, we track how many subarrays from index i lead to a valid sum.
Let’s walk through an example to clarify this process. Suppose nums = [1, 0, 1, 0, 1] and goal = 2. Using the loops:
- At i = 0, inner loop adds:
- nums[0] → sum = 1
- nums[1] → sum = 1
- nums[2] → sum = 2
- nums[3] → sum = 2
- nums[4] → sum = 3
- At i = 1, inner loop adds:
- nums[1] → sum = 0
- nums[2] → sum = 1
- nums[3] → sum = 1
- nums[4] → sum = 2
- At i = 2, inner loop adds:
- nums[2] → sum = 1
- nums[3] → sum = 1
- nums[4] → sum = 2
- At i = 3, inner loop adds:
- nums[3] → sum = 0
- nums[4] → sum = 1
- At i = 4, inner loop adds:
- nums[4] → sum = 1
This way, we identify 4 valid subarrays with sum exactly equal to goal.
This nested loop approach checks every possible subarray, and gives us a solid understanding of how subarray sums work in problems like this. Though not optimal in terms of time, it builds strong fundamentals and helps us move confidently toward optimized solutions later.
After forming subarrays using the nested loops, the next step is to check whether the running sum is equal to the given goal. Since the array only contains 0s and 1s, calculating the sum is straightforward — we simply add each element while expanding the subarray from a fixed starting point. Whenever the running sum becomes equal to the goal, we’ve identified a valid subarray and increment our count.
For example, take nums = [1, 0, 1, 0, 1] and goal = 2. Some valid subarrays whose sums equal the goal are:
- [1, 0, 1] → sum = 2
- [0, 1, 0, 1] → sum = 2
- [1, 0, 1, 0] → sum = 2
- [1, 0, 1] (again, starting at index 2) → sum = 2
Each time we find a subarray where the sum matches the goal, we increase the count. This exhaustive approach ensures that all valid subarrays are captured.
Approach
Step 1: Fix the Starting Index of the Subarray
We start with an outer loop that picks the starting index start of the subarray.
This loop goes from start = 0 to start < nums.size(), so we can consider every possible subarray in the array.
Step 2: Use an Inner Loop to Expand the Subarray and Calculate the Sum
For every fixed starting index, we use an inner loop to expand the subarray to the right.
We keep adding nums[end] to a variable current_sum.
This loop runs from end = start to end < nums.size().
At every step, we check if current_sum == goal. If yes, we increase our count by 1.
Step 3: Continue Until the End of Array
Even if we find a valid subarray, we don’t stop. We continue the inner loop to check for other subarrays starting from the same start.
This way, we make sure we count all valid subarrays that sum up to the given goal.
Step 4: After All Loops, Return the Final Count
Once both loops are done, we return the final count of subarrays that had a sum equal to goal.
This count is our answer.

Dry Run
Let’s do a detailed dry run of the brute-force approach using two nested loops for the input:
nums = [1, 0, 1, 0, 1], goal = 2
We want to find all subarrays whose sum equals 2.
Step 1: Loop Over All Possible Subarrays
We use two nested loops:
- Outer loop: fix the starting index
- Inner loop: expand the ending index, summing elements along the way
If the sum equals the goal, we increment the count.
Iteration-Wise Dry Run
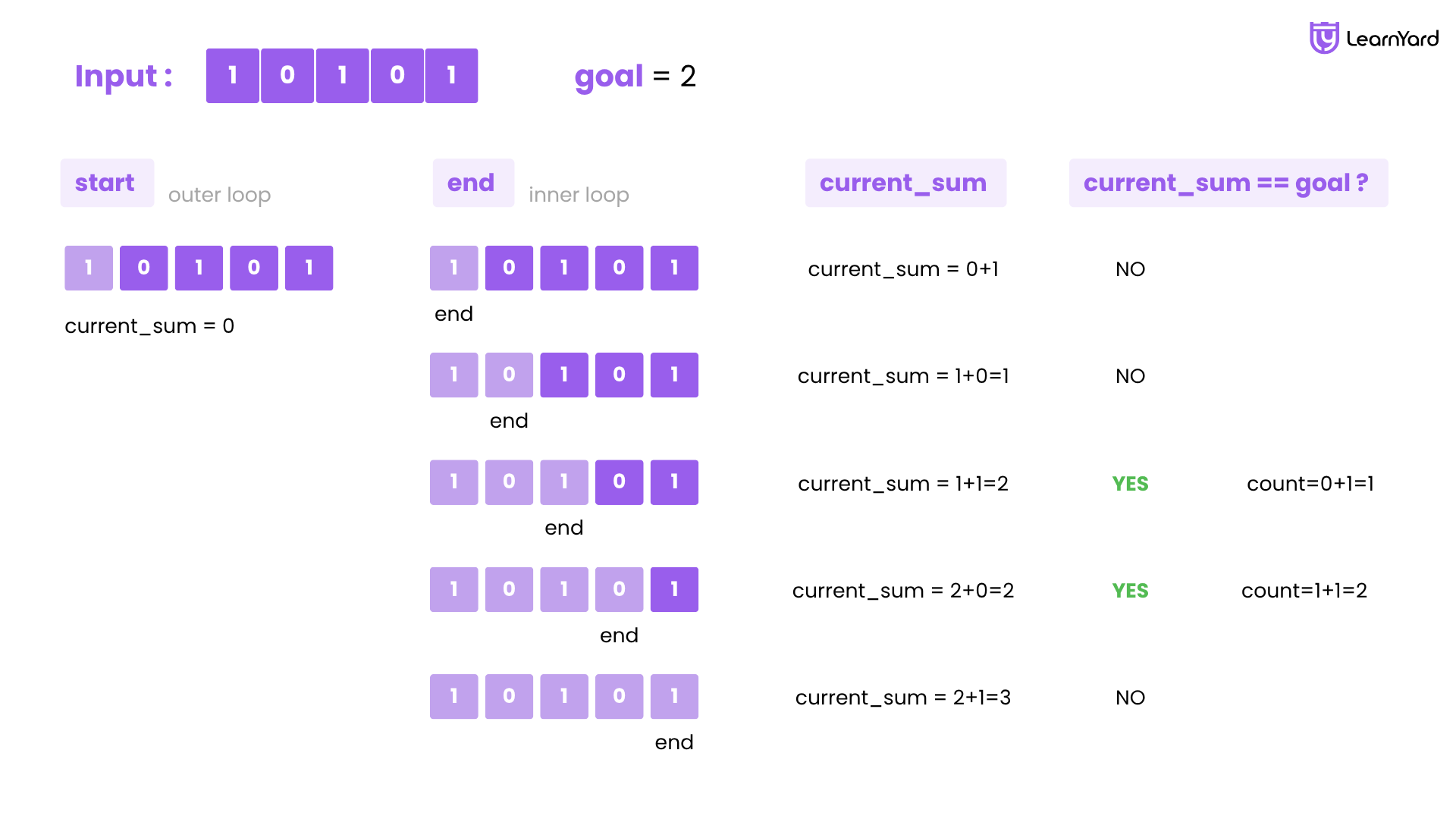
start = 0
- end = 0 → sum = 1 → Not equal
- end = 1 → sum = 1 + 0 = 1 → Not equal
- end = 2 → sum = 1 + 0 + 1 = 2 → Match → count = 1
- end = 3 → sum = 3 → Exceeds → skip
- end = 4 → sum = 4 → skip
start = 1
- end = 1 → sum = 0 → Not equal
- end = 2 → sum = 0 + 1 = 1 → Not equal
- end = 3 → sum = 0 + 1 + 0 = 1 → Not equal
- end = 4 → sum = 0 + 1 + 0 + 1 = 2 → Match → count = 2
start = 2
- end = 2 → sum = 1 → Not equal
- end = 3 → sum = 1 + 0 = 1 → Not equal
- end = 4 → sum = 1 + 0 + 1 = 2 → Match → count = 3
start = 3
- end = 3 → sum = 0 → Not equal
- end = 4 → sum = 0 + 1 = 1 → Not equal
start = 4
- end = 4 → sum = 1 → Not equal
Final Result
The total number of subarrays whose sum is equal to 2 is:
count = 3
Valid subarrays:
- nums[0..2] = [1, 0, 1]
- nums[1..4] = [0, 1, 0, 1]
- nums[2..4] = [1, 0, 1]
Code for All Languages
C++
#include <iostream> // For cin and cout
#include <vector> // For using the vector data structure
using namespace std;
class Solution {
public:
int numSubarraysWithSum(vector<int>& nums, int goal) {
int count = 0;
int n = nums.size();
// Step 1: Outer loop to fix the starting index
for (int start = 0; start < n; ++start) {
int current_sum = 0;
// Step 2: Inner loop to compute sum of subarray from start to end
for (int end = start; end < n; ++end) {
current_sum += nums[end];
// Step 3: Check if current subarray sum equals the goal
if (current_sum == goal) {
++count;
}
}
}
// Step 4: Return total count of subarrays with sum equal to goal
return count;
}
};
int main() {
int n, goal;
// Step 1: Read array size and goal value
cin >> n >> goal;
vector<int> nums(n);
// Step 2: Read binary array values
for (int i = 0; i < n; ++i) {
cin >> nums[i];
}
// Step 3: Create instance of Solution class and call the function
Solution sol;
int result = sol.numSubarraysWithSum(nums, goal);
// Step 4: Print the result (number of valid subarrays)
cout << result << endl;
return 0;
}
Java
import java.util.Scanner; // For reading input
public class Main {
public int numSubarraysWithSum(int[] nums, int goal) {
int count = 0;
int n = nums.length;
// Step 1: Outer loop to fix the starting index
for (int start = 0; start < n; ++start) {
int current_sum = 0;
// Step 2: Inner loop to compute sum of subarray from start to end
for (int end = start; end < n; ++end) {
current_sum += nums[end];
// Step 3: Check if current subarray sum equals the goal
if (current_sum == goal) {
count++;
}
}
}
// Step 4: Return total count of subarrays with sum equal to goal
return count;
}
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
// Step 1: Read array size and goal value
int n = sc.nextInt();
int goal = sc.nextInt();
// Step 2: Read binary array elements
int[] nums = new int[n];
for (int i = 0; i < n; i++) {
nums[i] = sc.nextInt();
}
// Step 3: Create instance of Main class and call the function
Main sol = new Main();
int result = sol.numSubarraysWithSum(nums, goal);
// Step 4: Print the result
System.out.println(result);
}
}
Python
class Solution:
def numSubarraysWithSum(self, nums, goal):
count = 0
n = len(nums)
# Step 1: Outer loop to fix the starting index
for start in range(n):
current_sum = 0
# Step 2: Inner loop to compute sum of subarray from start to end
for end in range(start, n):
current_sum += nums[end]
# Step 3: Check if current subarray sum equals the goal
if current_sum == goal:
count += 1
# Step 4: Return total count of subarrays with sum equal to goal
return count
if __name__ == "__main__":
# Step 1: Read array size and goal value
n, goal = map(int, input().split())
# Step 2: Read the binary array
nums = list(map(int, input().split()))
# Step 3: Create Solution object and compute the result
sol = Solution()
result = sol.numSubarraysWithSum(nums, goal)
# Step 4: Print the result
print(result)
Javascript
/**
* @param {number[]} nums - Binary array
* @param {number} goal - Target sum
* @return {number} - Number of subarrays with sum equal to goal
*/
var numSubarraysWithSum = function(nums, goal) {
let count = 0;
let n = nums.length;
// Step 1: Outer loop to fix the starting index
for (let start = 0; start < n; ++start) {
let current_sum = 0;
// Step 2: Inner loop to compute sum of subarray from start to end
for (let end = start; end < n; ++end) {
current_sum += nums[end];
// Step 3: Check if current subarray sum equals the goal
if (current_sum === goal) {
count++;
}
}
}
// Step 4: Return total count of subarrays with sum equal to goal
return count;
};
// Driver code using readline for Node.js
const readline = require("readline");
const rl = readline.createInterface({
input: process.stdin,
output: process.stdout
});
let input = [];
rl.on("line", function(line) {
input.push(line.trim());
// Step 1: Expecting 2 lines: First for n & goal, second for array
if (input.length === 2) {
const [n, goal] = input[0].split(" ").map(Number); // Parse n and goal
const nums = input[1].split(" ").map(Number); // Parse array
// Step 2: Call function
const result = numSubarraysWithSum(nums, goal);
// Step 3: Print result
console.log(result);
rl.close();
}
});
Time Complexity: O(n²)
Outer Loop: O(n)
The outer loop runs from index start = 0 to start < nums.length.
Let’s denote:
- n = length of the array nums
So, the loop executes n times in the worst case.
Inner Loop: O(n - start)
For each iteration of the outer loop, the inner loop runs from end = start to end < n.
This takes O(n - start) time per outer iteration.
Total Iterations of Inner Loop: O(n²)
The inner loop runs a total of n + (n-1) + (n-2) + ... + 1 = n(n + 1)/2 times, which is O(n²) overall.
Subarray Sum and Comparison: O(1)
In each inner iteration, we add one element and compare the sum with the goal.
Both operations are constant time: O(1).
Total Time per Outer Loop Iteration: O(n)
Each outer loop iteration performs up to O(n) inner steps.
Final Time Complexity: O(n²)
We perform O(n) work for each of the O(n) starting positions in the array.
So, the total time complexity is: O(n²)
Where:
- n is the length of the array nums
Space Complexity: O(1)
Auxiliary Space Complexity: O(1)
This refers to any extra space used by the algorithm that is independent of the input and output space.
In our brute-force approach, we use:
- A few integer variables like count, current_sum, start, and end.
- No dynamic data structures or additional arrays are used within the loops.
All variables occupy constant space, and no additional memory grows with the size of the input.
Hence, the auxiliary space complexity is O(1).
Total Space Complexity: O(n)
This includes the space required for:
- Input space: We store the input binary array nums of size n. So, input space is O(n).
- Output space: We only return a single integer (the count), so this is O(1).
- Extra space used by the algorithm: As analyzed above, O(1).
Combining all the space requirements:
Total Space Complexity = O(n) + O(1) + O(1) = O(n)
Why this Approach will give TLE?
The main reason this approach is slow and can time out is because of its high time complexity combined with the input size constraints.
The length of the array nums can be as large as 30,000 (3 * 10^4), then:
The brute-force method uses two nested loops, making it O(n²) time complexity.
This means for each starting index, we check all possible subarrays ending at or after that index.
So, the total number of operations in the worst case becomes:
n ≈ 30,000 → Total subarrays ≈ (n * (n + 1)) / 2 = (30,000 * 30,001) / 2 ≈ 450,015,000 operations
This is over 450 million subarrays being evaluated.
Each subarray sum operation requires addition, and the check for goal equality.
So we are performing over 450 million operations, even without any sorting involved.
Most competitive programming platforms like LeetCode or Codeforces set a time limit of 1–2 seconds or allow roughly 10^7 operations per second.
For large inputs, this brute-force solution will easily exceed the time limit, causing Time Limit Exceeded (TLE).
We’ve seen the brute-force approach, which checks all possible subarrays. It works, but it’s slow because of the nested loops. For large inputs, this can easily give TLE. Can we avoid checking every subarray? Can we use a smarter way to count subarrays with a given sum? Let’s look at a better approach using prefix sums and a hashmap.
Better Approach (Prefix Sum + HashMap)
Intuition
Once we’ve explored all subarrays using brute force, we start wondering — is there a way to avoid checking every single subarray? Can we somehow remember what we’ve seen so far and use it to make future calculations faster?
The answer lies in a powerful duo: Prefix Sums and HashMaps. Together, they help us avoid repeated work and count valid subarrays in linear time.
Why Prefix Sums?
A prefix sum is just the running total of the array elements as we go from left to right.
At every index i, it tells us the sum of elements from the start of the array up to i.
This is powerful because:
- If we know the sum from 0 to j, and we also know the sum from 0 to i-1, then the sum of the subarray nums[i..j] is just:cssCopyEditprefixSum[j] - prefixSum[i - 1]
Why Use a HashMap?
A HashMap helps us remember how many times each prefix sum has occurred as we move through the array.
Instead of checking all previous subarrays manually, we just ask:
“How many times have I seen a prefix sum that would make the current subarray sum equal to the goal?”
If we find such a sum in the map, we instantly know how many valid subarrays end at the current position.
Generating Valid Subarrays Using Prefix Sum and HashMap
To implement this, we initialize:
- A counter count to keep track of the number of valid subarrays.
- A running sum currSum initialized to 0.
- A HashMap mp to store frequencies of prefix sums we’ve seen so far.
We start by inserting {0 → 1} to handle the case when a prefix itself directly matches the goal.
Now, we walk through each element in nums:
- Add the current number to currSum.
- Compute currSum - goal. This represents the prefix sum we want to find — if such a prefix existed earlier, then the subarray between that earlier index and the current index sums up to the goal.
- Look up how many times (currSum - goal) has occurred in the map — this is exactly how many valid subarrays end here.
- Add this number to count.
- Finally, update the map with the new currSum.
This way, we don’t need to recompute sums from scratch — we just use what we already know.
Let’s walk through an example to clarify this process. Suppose nums = [1, 0, 1, 0, 1] and goal = 2.
We maintain a prefix sum and update it while traversing:
- After reading 1: currSum = 1, currSum - goal = -1, not found in map
→ count = 0, map = {0:1, 1:1} - After reading 0: currSum = 1, currSum - goal = -1, still not found
→ count = 0, map = {0:1, 1:2} - After reading 1: currSum = 2, currSum - goal = 0, found once
→ count = 1, map = {0:1, 1:2, 2:1} - After reading 0: currSum = 2, currSum - goal = 0, found again
→ count = 2, map = {0:1, 1:2, 2:2} - After reading 1: currSum = 3, currSum - goal = 1, found twice
→ count = 4, map = {0:1, 1:2, 2:2, 3:1}
We identify 4 valid subarrays — same as brute force, but much faster
Why Is This So Efficient?
Instead of exploring all subarrays explicitly, we “reuse” earlier knowledge.
Every time we reach a new index, we ask: How many valid starting points exist for a subarray ending here with sum = goal?
The map gives us an instant answer.
And since each element is processed only once, our total time complexity is O(n).
This approach is optimal for problems like these — where we’re counting subarrays with a fixed sum — and it combines mathematical insight (prefix sums) with smart storage (hashmap) to deliver powerful results efficiently.
Approach
Step 1: Initialize Variables to Track Prefix Sum and Frequency
We start by initializing a few key variables:
- currSum = 0: This keeps track of the running prefix sum as we iterate through the array.
- count = 0: This will store our final answer — the total number of valid subarrays.
- mp = {0: 1}: A hashmap (or dictionary) to store the frequency of prefix sums we’ve seen so far.
We initialize it with {0: 1} to account for subarrays that themselves sum exactly to the goal from the start.
Step 2: Traverse the Array and Update the Prefix Sum
We loop through each element in nums. For each element:
- Add the element to currSum to update the running prefix sum.
- This indicates a subarray ending at the current index sums to goal.
- If currSum - goal exists in the hashmap mp: Add the frequency of that value to count.
Step 3: Update the HashMap with the Current Prefix Sum
After checking for valid subarrays, we update the hashmap:
- Increment the frequency of the current prefix sum currSum in mp.
- This ensures future elements can refer back to it when needed.
Step 4: Continue the Process Until the End of the Array
We repeat the same steps for every element in the array.
This way, we keep expanding the ending index of subarrays while using the hashmap to efficiently check for all valid starting points.
Step 5: Return the Final Count
Once we finish iterating through the array, the variable count contains the total number of subarrays whose sum equals the target goal.
We return this value as our answer.
Dry Run
Let’s do a detailed dry run of the Prefix Sum + HashMap approach
Input:
nums = [1, 0, 1, 0, 1], goal = 2
We want to find all subarrays whose sum equals 2.
Step 1: Initialize Required Variables
We set up:
- currSum = 0 → running prefix sum
- count = 0 → to store total number of valid subarrays
- mp = {0: 1} → hashmap to store frequencies of prefix sums seen so far
Why {0:1}?
Because if at any point currSum == goal, that entire subarray from the beginning is valid, and we should count it.
Step 2: Traverse the Array
Let’s iterate through the array one element at a time and apply the logic.
Iteration-Wise Dry Run
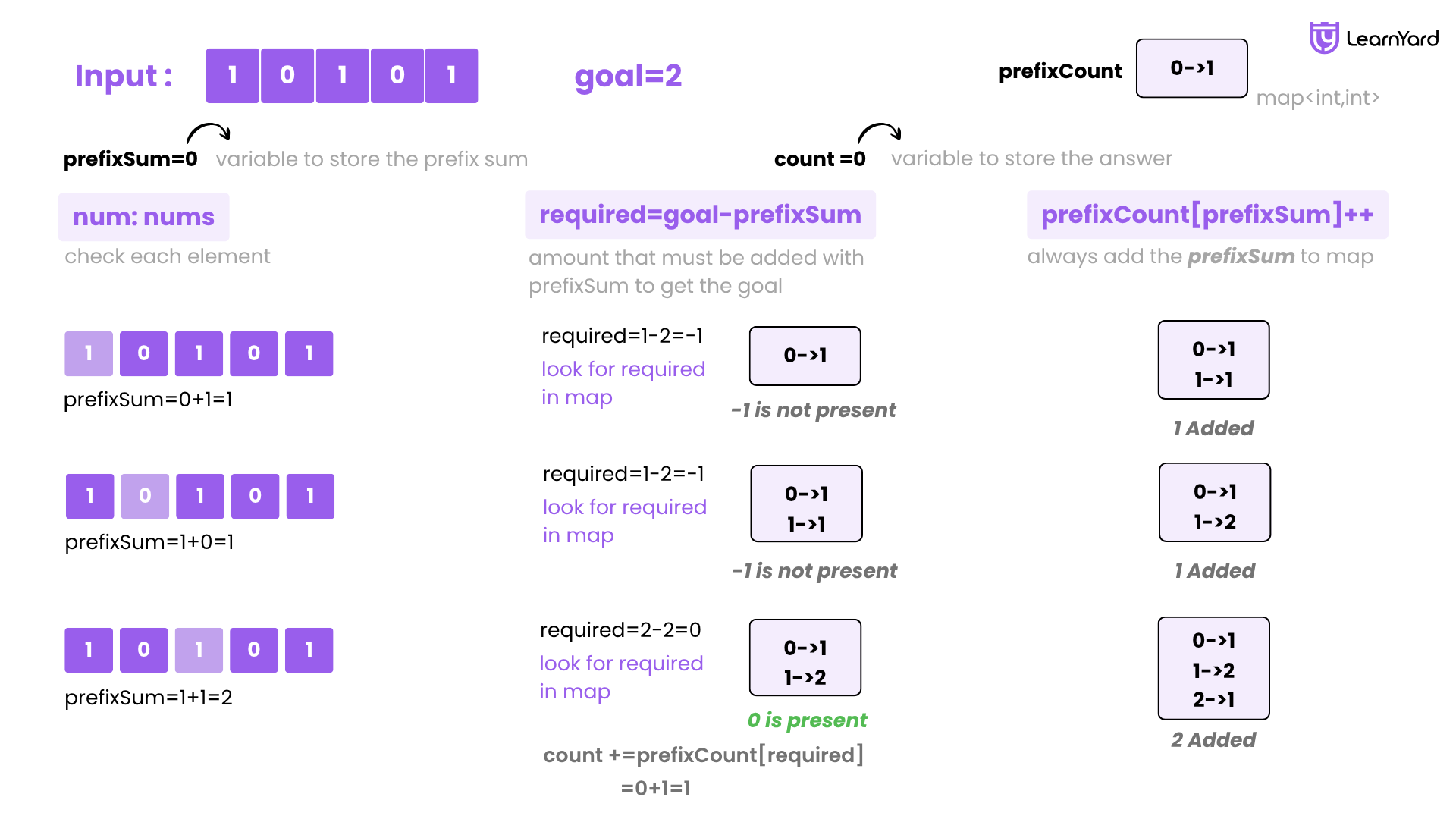
i = 0, nums[0] = 1
- currSum = 0 + 1 = 1
- Check if currSum - goal = 1 - 2 = -1 exists in mp → No
- So, count stays 0
- Update mp[1] = 1 → mp = {0: 1, 1: 1
}
i = 1, nums[1] = 0
- currSum = 1 + 0 = 1
- Check if 1 - 2 = -1 exists in mp → No
- count = 0
- Update mp[1] = 2 → mp = {0: 1, 1: 2
i = 2, nums[2] = 1
- currSum = 1 + 1 = 2
- Check if 2 - 2 = 0 exists in mp → Yes, mp[0] = 1
- So, count += 1 → count = 1
- Update mp[2] = 1 → mp = {0: 1, 1: 2, 2: 1}
Found subarray ending at index 2 with sum 2
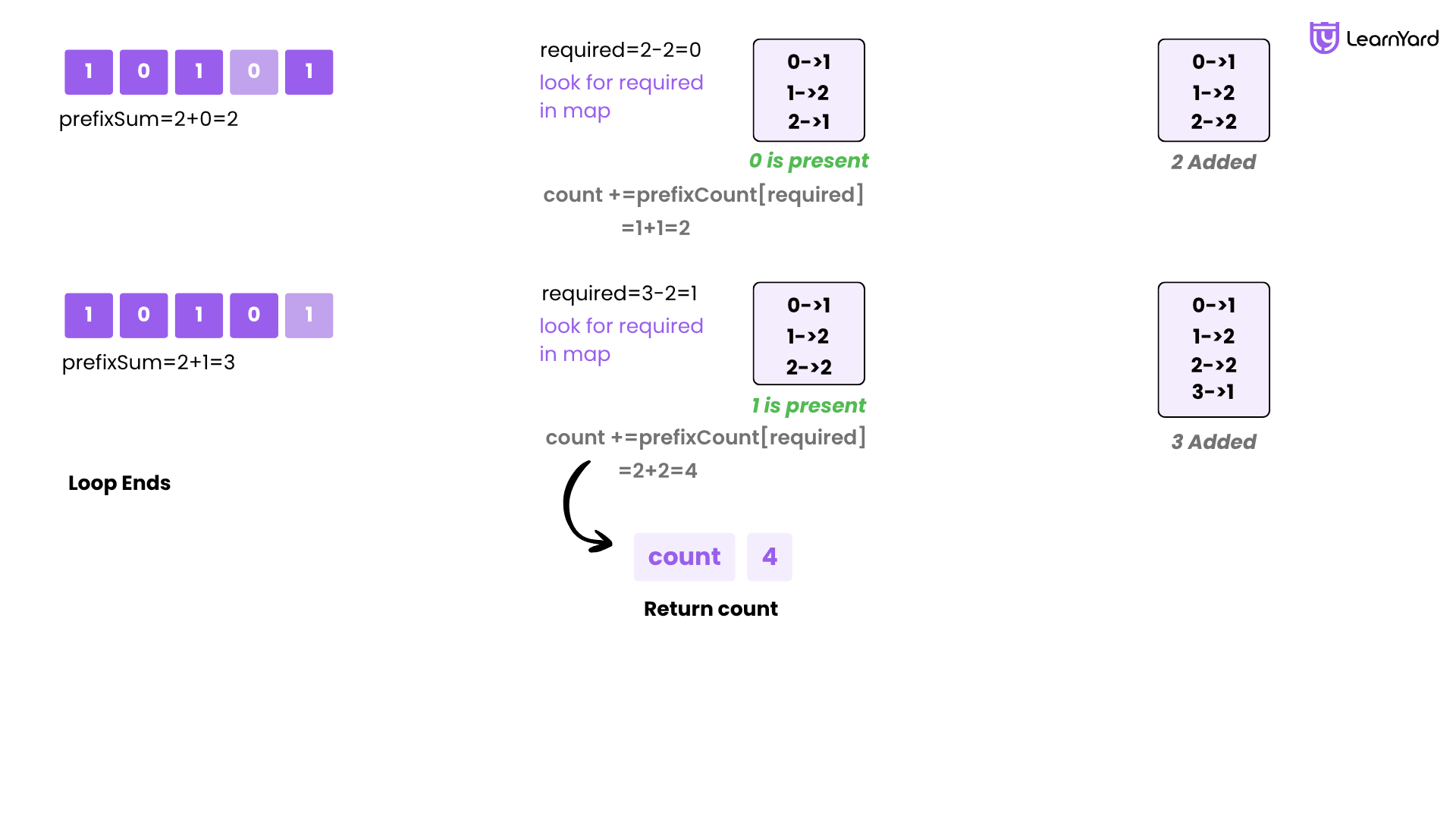
i = 3, nums[3] = 0
- currSum = 2 + 0 = 2
- Check if 2 - 2 = 0 exists in mp → Yes, mp[0] = 1
- count += 1 → count = 2
- Update mp[2] = 2 → mp = {0: 1, 1: 2, 2: 2}
Found another subarray ending at index 3 with sum 2
i = 4, nums[4] = 1
- currSum = 2 + 1 = 3
- Check if 3 - 2 = 1 exists in mp → Yes, mp[1] = 2
- count += 2 → count = 4
- Update mp[3] = 1 → mp = {0: 1, 1: 2, 2: 2, 3: 1}
Found two subarrays ending at index 4 with sum 2
Final Result
The total number of subarrays whose sum is equal to 2 is:
count = 4
Valid Subarrays Identified:
(Found using prefix sums, but can be listed as:)
- nums[0..2] = [1, 0, 1]
- nums[1..4] = [0, 1, 0, 1]
- nums[2..4] = [1, 0, 1]
- nums[3..4] = [0, 1]
Note: The power of prefix sum + hashmap lies in not needing to manually walk through each subarray. It just smartly uses what’s been seen before to instantly recognize valid ones!
Code for All Languages
C++
#include <iostream> // For standard I/O
#include <vector> // For using the vector container
#include <unordered_map> // For using the hashmap (unordered_map)
using namespace std;
class Solution {
public:
int numSubarraysWithSum(vector<int>& nums, int goal) {
unordered_map<int, int> prefixCount; // Stores frequency of each prefix sum
prefixCount[0] = 1; // Base case: prefix sum 0 seen once
int prefixSum = 0; // Running prefix sum
int count = 0; // Total number of valid subarrays
// Iterate over the array
for (int num : nums) {
prefixSum += num; // Update running sum
// Check if (prefixSum - goal) exists in the map
if (prefixCount.find(prefixSum - goal) != prefixCount.end()) {
count += prefixCount[prefixSum - goal]; // Add all subarrays ending here with sum == goal
}
// Update the prefix sum frequency
prefixCount[prefixSum]++;
}
return count;
}
};
int main() {
int n, goal;
cin >> n >> goal; // Input size and goal
vector<int> nums(n);
// Input the binary array
for (int i = 0; i < n; ++i) {
cin >> nums[i];
}
Solution sol;
cout << sol.numSubarraysWithSum(nums, goal) << endl;
return 0;
}
Java
import java.util.*; // For Map, HashMap, Scanner
class Solution {
public int numSubarraysWithSum(int[] nums, int goal) {
Map<Integer, Integer> prefixCount = new HashMap<>(); // Prefix sum frequency map
prefixCount.put(0, 1); // Base case
int prefixSum = 0;
int count = 0;
// Traverse through the array
for (int num : nums) {
prefixSum += num; // Update running sum
// Check if (prefixSum - goal) was seen before
if (prefixCount.containsKey(prefixSum - goal)) {
count += prefixCount.get(prefixSum - goal);
}
// Record the prefixSum
prefixCount.put(prefixSum, prefixCount.getOrDefault(prefixSum, 0) + 1);
}
return count;
}
}
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt(); // Size of the array
int goal = sc.nextInt(); // Target sum
int[] nums = new int[n];
// Read the binary array
for (int i = 0; i < n; ++i) {
nums[i] = sc.nextInt();
}
Solution sol = new Solution();
System.out.println(sol.numSubarraysWithSum(nums, goal));
}
}
Python
from typing import List # For List type hinting
from collections import defaultdict # For default dictionary to track prefix sums
class Solution:
def numSubarraysWithSum(self, nums: List[int], goal: int) -> int:
prefix_count = defaultdict(int) # Map to store frequency of prefix sums
prefix_count[0] = 1 # Base case
prefix_sum = 0
count = 0
# Iterate over the array
for num in nums:
prefix_sum += num # Update the running sum
# Check if (prefix_sum - goal) is in the map
count += prefix_count[prefix_sum - goal]
# Update prefix count
prefix_count[prefix_sum] += 1
return count
# Driver Code
if __name__ == "__main__":
n, goal = map(int, input().split()) # Read array size and goal
nums = list(map(int, input().split())) # Read the binary array
sol = Solution()
print(sol.numSubarraysWithSum(nums, goal)) # Output the result
Javascript
/**
* @param {number[]} nums - Input binary array
* @param {number} goal - Target sum
* @return {number} - Number of subarrays whose sum equals goal
*/
var numSubarraysWithSum = function(nums, goal) {
let prefixCount = new Map(); // Map to store frequency of prefix sums
prefixCount.set(0, 1); // Base case
let prefixSum = 0;
let count = 0;
// Iterate through the array
for (let num of nums) {
prefixSum += num; // Update the running sum
// Check if (prefixSum - goal) was seen before
if (prefixCount.has(prefixSum - goal)) {
count += prefixCount.get(prefixSum - goal);
}
// Update prefixCount map
prefixCount.set(prefixSum, (prefixCount.get(prefixSum) || 0) + 1);
}
return count;
};
// Driver Code
const readline = require("readline");
const rl = readline.createInterface({
input: process.stdin,
output: process.stdout
});
let inputs = [];
rl.on("line", function(line) {
inputs.push(line.trim());
if (inputs.length === 2) {
const [n, goal] = inputs[0].split(' ').map(Number); // First line: size and goal
const nums = inputs[1].split(' ').map(Number); // Second line: binary array
const result = numSubarraysWithSum(nums, goal); // Compute result
console.log(result); // Print result
rl.close();
}
});
Time Complexity: O(n)
- Outer Loop: O(n)
- Traverse the array once from left to right.
- Let n be the length of the array nums.
- Loop runs n times in the worst case.
- Prefix Sum Computation: O(1)
- For each element, add it to a running total (currSum += nums[i]).
- This is a constant-time operation.
- HashMap Lookup and Update: O(1) (Amortized)
- At each step:
- Lookup: Check if currSum - goal exists in the hashmap.
- Update: Increment the frequency of currSum in the hashmap.
- Both operations take O(1) time on average due to Python’s dictionary performance.
- Total Work Done Per Iteration: O(1)
- Add to currSum → O(1)
- Lookup in mp → O(1)
- Update mp → O(1)
- Increment count if a valid subarray is found → O(1)
- Total per element = O(1)
- Final Time Complexity: O(n)
- Do constant work for each of the
nelements. - Total time = O(n)
- Do constant work for each of the
- Where:
- n = length of the input array nums
- HashMap enables constant-time average lookup and update
- Efficient for large input sizes
Space Complexity: O(n)
- Auxiliary Space Complexity: O(n)
- Refers to extra space used by the algorithm, excluding input/output.
- Uses a few integer variables: currSum, count, and loop index → O(1)
- Uses a hashmap mp to store frequency of prefix sums.
- In the worst case, prefix sums can be unique at each index → up to n entries.
- Hashmap space = O(n)
- Total Space Complexity: O(n)
- Input space: array nums of size n → O(n)
- Output space: return value (count) → O(1)
- Extra algorithm space:
- Hashmap for prefix sums → O(n)
- A few integer variables → O(1)
- Combined:
- Total space = O(n) + O(1) + O(n) = O(n)
- Where:
- n = number of elements in the input array nums
- Hashmap may hold up to
nunique prefix sums in worst case
We’ve seen how prefix sums with a hashmap give us a big boost over the brute-force method — no more nested loops! But there’s still room to optimize further.
Since the array only contains 0s and 1s, we can use this special property to our advantage. Instead of using a hashmap, can we slide a window and keep track of sums more directly? Let’s explore an even more optimized approach using the Sliding Window technique to count subarrays in linear time with minimal extra space.
Optimal Approach
Intuition
After optimizing with prefix sums and hashmaps, we might still ask — is there a way to avoid using extra space like hashmaps? Can we simplify the logic even more?
For binary arrays (arrays with only 0s and 1s), the answer is yes — using a sliding window. This technique lets us count subarrays without generating them, and without storing prefix sums or hashmaps.
But there’s a small trick here: instead of directly counting subarrays with exactly goal 1s, we count subarrays with at most k 1s.
Why Use AtMost Logic?
The idea is simple:
Number of subarrays with exactly k 1s = Number of subarrays with at most k 1s − Number of subarrays with at most k - 1 1s
This transformation works perfectly in binary arrays, because counting “at most k 1s” can be done easily using the sliding window technique.
How Sliding Window Helps?
- Maintain a sliding window [left, right] where the number of 1s in the window is at most k.
- Move right forward one step at a time:
- Add the current number to the running count of 1s.
- If the count of 1s exceeds k:
- Move
leftforward until the window becomes valid again (i.e., number of 1s ≤ k).
- Move
- At each step:
- The number of valid subarrays ending at index right is right - left + 1.
- This counts all subarrays that start from indices left, left + 1, ..., up to right and end at right.
- Add this count to the total.
- Example:
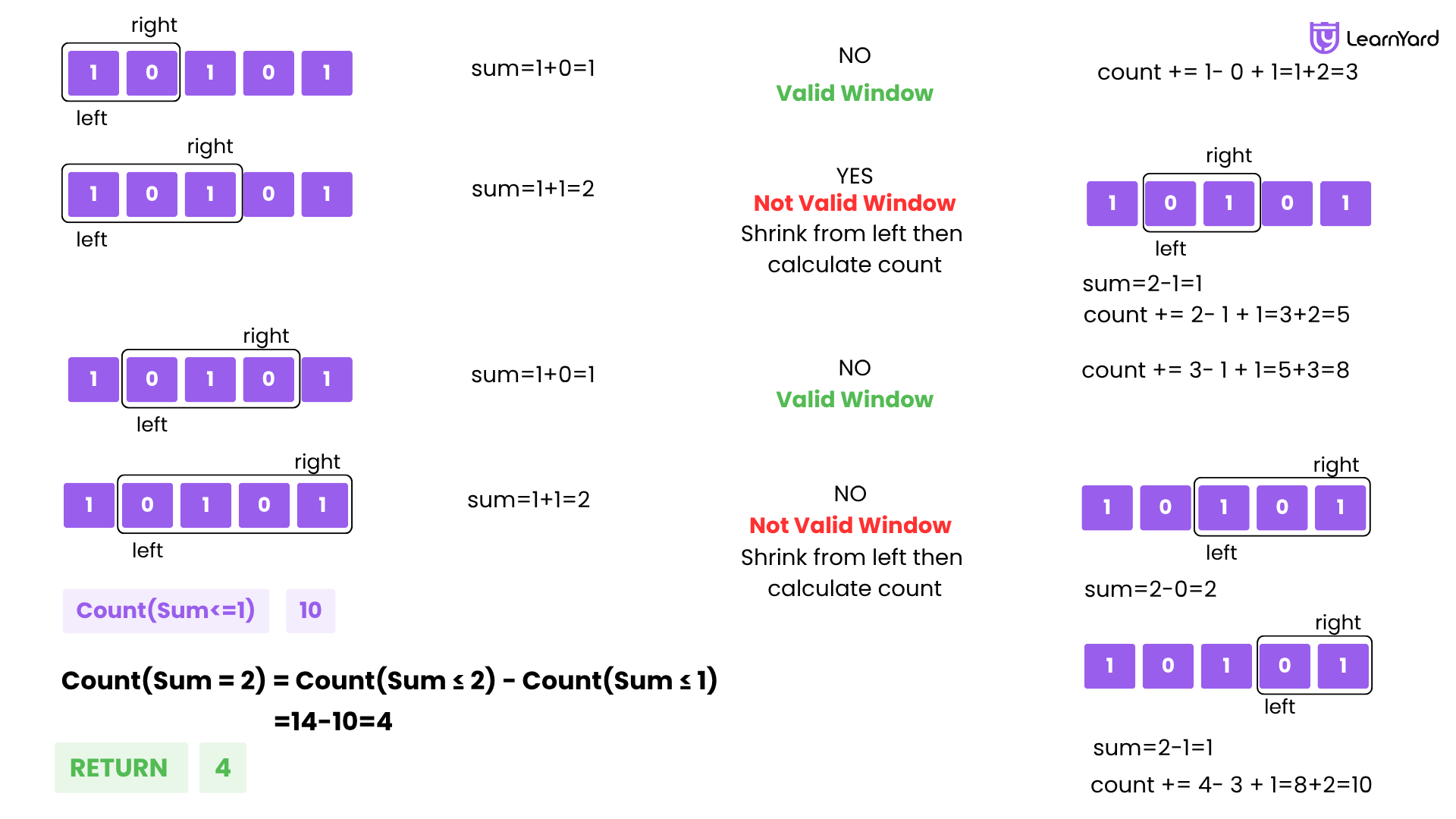
- Given: nums = [1, 0, 1, 0, 1], goal = 2
- Compute atMost(2):
- right = 0: window = [1], sum = 1 → valid → count += 1
- right = 1: window = [1, 0], sum = 1 → valid → count += 2
- right = 2: window = [1, 0, 1], sum = 2 → valid → count += 3
- right = 3: window = [1, 0, 1, 0], sum = 2 → valid → count += 4
- right = 4: window = [1, 0, 1, 0, 1], sum = 3 → too many 1s → move left → sum = 2 → count += 4
- Final atMost(2) = 14
- Compute atMost(1):
- Final result = 10
- Final Answer:
- exactly(goal) = atMost(2) - atMost(1) = 14 - 10 = 4
- Key Benefit:
- Logic is simpler and space usage is constant (no extra data structures used)
Why Is This So Efficient?
Every element is added to the window once and removed at most once.
So the total time complexity is O(n), and space complexity is O(1).
There are no hashmaps, no prefix arrays — just two pointers and simple math.
This makes it one of the fastest and cleanest solutions for counting subarrays with a fixed number of 1s in a binary array.
Approach
Step 1: Define a Helper Function to Count Subarrays With At Most K 1s
We start by defining a helper function called atMost(k) that returns the number of subarrays with at most k ones.
This function uses a sliding window technique:
- A left pointer that marks the start of the window
- A right pointer that moves forward as we traverse the array
- A counter count to keep track of valid subarrays
- A variable ones to count how many 1s are currently inside the window
Step 2: Traverse the Array Using the Sliding Window
We loop through each element in the array using the right pointer.
For each element:
- If the current number is 1, increment the ones count
- While the number of 1s in the window is greater than k, move the left pointer forward and subtract the value at nums[left] from the ones count
- At each step, all subarrays from left to right are valid, so we add (right - left + 1) to the result
This gives us the total number of subarrays with at most k 1s.
Step 3: Use Inclusion-Exclusion to Get Exactly K 1s
We now apply a simple trick to get the number of subarrays with exactly k 1s:
exactly(k) = atMost(k) - atMost(k - 1)
This works because:
- atMost(k) counts all subarrays with 0, 1, ..., k 1s
- atMost(k - 1) counts all subarrays with 0, 1, ..., (k - 1) 1s
- Subtracting the two gives only the subarrays with exactly k 1s
Step 4: Return the Final Answer
After computing exactly(k) using the difference of two sliding window results, we return that as the final answer.
This represents the number of subarrays in nums whose sum is exactly equal to goal.


Dry Run
Input:
nums = [1, 0, 1, 0, 1]
goal = 2
We are to count the number of subarrays whose sum is exactly 2.
Step-by-step Setup:
We will maintain:
- prefix_sum: Running sum of elements seen so far
- count: Total number of valid subarrays found
- freq: A hashmap (or dictionary) to keep track of how many times a given prefix_sum has occurred
We initialize:
- prefix_sum = 0
- count = 0
- freq = { 0: 1 } → This means there's one way to get sum 0 (an empty prefix)
Now we iterate over the array step by step.
Iteration 1:
Index = 0
Element = 1
prefix_sum = 0 + 1 = 1
Now check: prefix_sum - goal = 1 - 2 = -1
Is -1 in freq? → No
So count remains 0
Update freq: Add 1 to freq[1] → freq becomes {0:1, 1:1}
Iteration 2:
Index = 1
Element = 0
prefix_sum = 1 + 0 = 1
prefix_sum - goal = 1 - 2 = -1
Is -1 in freq? → No
count remains 0
Update freq: freq[1] += 1 → freq becomes {0:1, 1:2}
Iteration 3:
Index = 2
Element = 1
prefix_sum = 1 + 1 = 2
prefix_sum - goal = 2 - 2 = 0
Is 0 in freq? → Yes, freq[0] = 1
That means there is 1 subarray ending here with sum = goal
So count = count + 1 = 1
Update freq: freq[2] = 1 → freq becomes {0:1, 1:2, 2:1}
Iteration 4:
Index = 3
Element = 0
prefix_sum = 2 + 0 = 2
prefix_sum - goal = 2 - 2 = 0
freq[0] = 1
So again, one more valid subarray found
count = 1 + 1 = 2
Update freq: freq[2] += 1 → freq becomes {0:1, 1:2, 2:2}
Iteration 5:
Index = 4
Element = 1
prefix_sum = 2 + 1 = 3
prefix_sum - goal = 3 - 2 = 1
freq[1] = 2
So two valid subarrays end here with sum = goal
count = 2 + 2 = 4
Update freq: freq[3] = 1 → freq becomes {0:1, 1:2, 2:2, 3:1}
Final values:
prefix_sum = 3
count = 4
freq = {0:1, 1:2, 2:2, 3:1}
Final Result:
The total number of subarrays with sum exactly equal to 2 is 4
Let's list them explicitly:
- [1, 0, 1] → indices 0–2
- [1, 0, 1, 0] → indices 0–3
- [0, 1, 0, 1] → indices 1–4
- [1, 0, 1] → indices 2–4
Each of these has sum = 2.
Code for All Languages
C++
#include <iostream>
#include <vector>
using namespace std;
class Solution {
public:
// Helper function: Counts number of subarrays with sum at most 'S'
int atMost(vector<int>& nums, int S) {
if (S < 0) return 0; // No valid subarrays if S < 0
int left = 0, sum = 0, count = 0;
int n = nums.size();
// Sliding window from left to right
for (int right = 0; right < n; ++right) {
sum += nums[right]; // Expand window by adding nums[right]
// Shrink window from left if the sum exceeds S
while (sum > S) {
sum -= nums[left]; // Remove nums[left] from sum
left++; // Move left pointer right
}
// All subarrays between left and right are valid
count += right - left + 1;
}
return count;
}
// Main function to calculate subarrays with sum exactly equal to 'goal'
int numSubarraysWithSum(vector<int>& nums, int goal) {
// Use inclusion-exclusion: atMost(goal) - atMost(goal - 1)
return atMost(nums, goal) - atMost(nums, goal - 1);
}
};
int main() {
int n, goal;
// Input number of elements and target sum
cin >> n >> goal;
vector<int> nums(n);
// Input the binary array
for (int i = 0; i < n; ++i) cin >> nums[i];
// Create solution object and compute result
Solution sol;
int result = sol.numSubarraysWithSum(nums, goal);
// Output the total number of valid subarrays
cout << result << endl;
return 0;
}
Java
import java.util.*;
class Solution {
// Helper method: Counts subarrays with sum at most S
public int atMost(int[] nums, int S) {
if (S < 0) return 0; // No subarrays if goal is negative
int left = 0, sum = 0, count = 0;
// Sliding window approach
for (int right = 0; right < nums.length; right++) {
sum += nums[right]; // Expand window by adding rightmost element
// Shrink window if sum exceeds S
while (sum > S) {
sum -= nums[left]; // Remove leftmost element from sum
left++; // Slide window forward
}
// Count all subarrays from left to right
count += right - left + 1;
}
return count;
}
// Main function to return subarrays with sum exactly equal to goal
public int numSubarraysWithSum(int[] nums, int goal) {
return atMost(nums, goal) - atMost(nums, goal - 1);
}
}
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
// Input number of elements and the goal
int n = sc.nextInt();
int goal = sc.nextInt();
int[] nums = new int[n];
// Read the binary array
for (int i = 0; i < n; i++) nums[i] = sc.nextInt();
// Compute result using solution class
Solution sol = new Solution();
int result = sol.numSubarraysWithSum(nums, goal);
// Output the number of valid subarrays
System.out.println(result);
}
}
Python
from typing import List
class Solution:
def atMost(self, nums: List[int], S: int) -> int:
# Helper function: Count subarrays with sum at most S
if S < 0:
return 0 # No valid subarrays if target is negative
left = 0
total = 0
count = 0
# Sliding window to maintain the window with sum <= S
for right in range(len(nums)):
total += nums[right] # Expand window by adding rightmost element
# Shrink window from the left if total exceeds S
while total > S:
total -= nums[left]
left += 1
# All subarrays between left and right are valid
count += right - left + 1
return count
def numSubarraysWithSum(self, nums: List[int], goal: int) -> int:
# Use sliding window to get exactly goal by: atMost(goal) - atMost(goal - 1)
return self.atMost(nums, goal) - self.atMost(nums, goal - 1)
# Driver code
if __name__ == "__main__":
# Input the number of elements and target sum
n, goal = map(int, input().split())
# Read binary array
nums = list(map(int, input().split()))
# Instantiate solution and compute result
sol = Solution()
result = sol.numSubarraysWithSum(nums, goal)
# Output the result
print(result)
Javascript
/**
* Function to calculate number of subarrays with exact sum equal to goal
* @param {number[]} nums - The binary array (contains only 0 and 1)
* @param {number} goal - Target sum
* @return {number} - Number of valid subarrays
*/
var numSubarraysWithSum = function(nums, goal) {
// Helper function to count subarrays with sum at most S
function atMost(S) {
if (S < 0) return 0;
let left = 0, sum = 0, count = 0;
// Sliding window from left to right
for (let right = 0; right < nums.length; right++) {
sum += nums[right]; // Expand window
// Shrink window while sum exceeds S
while (sum > S) {
sum -= nums[left];
left++;
}
// Count all subarrays from left to right
count += right - left + 1;
}
return count;
}
return atMost(goal) - atMost(goal - 1);
};
// Driver Code (Node.js style input/output)
const readline = require("readline");
const rl = readline.createInterface({
input: process.stdin,
output: process.stdout
});
let inputLines = [];
rl.on("line", function(line) {
inputLines.push(line.trim());
if (inputLines.length === 2) {
// Read number of elements and goal
const [n, goal] = inputLines[0].split(' ').map(Number);
// Read binary array
const nums = inputLines[1].split(' ').map(Number);
// Compute and print result
const result = numSubarraysWithSum(nums, goal);
console.log(result);
rl.close();
}
});
Time Complexity: O(n)
Outer Loop (Right Pointer Traversal): O(n)
- Traverse the array once from left to right using a right pointer.
- Let n be the length of the array nums.
- The loop runs n times in the worst case.
Inner Loop (Left Pointer Adjustment): O(n) (Worst Case)
- The left pointer only moves forward and each element is visited at most once by it.
- In the worst case, for each right, the left pointer may advance if sum > goal.
- So while nested, total work done by left pointer over the entire algorithm is at most
nsteps.
Prefix Sum Update: O(1)
- Add nums[right] to the current window sum (sum += nums[right]).
- This is a simple addition → constant-time operation.
Window Shrinking (While Loop): O(1) amortized per iteration
- The window shrinks by removing nums[left] from the sum and incrementing left.
- Since left only moves forward and each element is removed at most once, the amortized cost is O(1) per iteration.
Counting Subarrays: O(1)
- For each valid window, compute count += right - left + 1.
- This is a constant-time arithmetic operation.
Total Work Done Per Iteration: O(1)
- Add to sum → O(1)
- Shrink window if needed → O(1) amortized
- Count valid subarrays in window → O(1)
- Total per element = O(1)
Final Time Complexity: O(n)
- Each element is visited at most twice (once by right, once by left).
- All other operations inside the loop are constant time.
- So the total time complexity is O(n).
Where:
- n = length of the input array nums
- No extra data structures like hash maps are needed
- Efficient for large inputs due to linear time and constant space
Space Complexity: O(1)
Auxiliary Space Complexity: O(1)
This refers to the extra space used by the algorithm, not counting the input or output.
Variables Used:
We use only a small number of simple variables throughout the algorithm:
- sum – to keep track of the number of 1s in the current window → O(1)
- count – accumulates the number of valid subarrays → O(1)
- left, right – pointers used for window boundaries → O(1)
No Additional Data Structures:
Unlike approaches that use a hashmap or prefix sums, this method uses no dynamic or auxiliary data structures.
- No arrays, no maps, no sets.
- Everything is handled with basic integer variables and simple arithmetic.
Total Space Complexity: O(1)
Input Space:
- Input array nums of size n → O(n)
(This is not included in auxiliary space; it’s considered part of the input.)
Output Space:
- The function returns a single integer (count) → O(1)
Extra Space Used by Algorithm:
- Only a constant number of integer variables → O(1)
Putting It All Together:
Total space = O(1) auxiliary + O(n) input + O(1) output
But since input and output space are not part of auxiliary analysis:
Final space complexity = O(1)
Where:
- n is the length of the input array nums
- No memory usage scales with input size
- This makes the sliding window method highly space-efficient, especially for large input arrays
Learning Tip
Now we have successfully tackled this problem, let's try these similar problems.
You are given a binary array nums.
A subarray of an array is good if it contains exactly one element with the value 1.
Return an integer denoting the number of ways to split the array nums into good subarrays. As the number may be too large, return it modulo 10^9 + 7.
A subarray is a contiguous non-empty sequence of elements within an array.
The score of an array is defined as the product of its sum and its length.
- For example, the score of [1, 2, 3, 4, 5] is (1 + 2 + 3 + 4 + 5) * 5 = 75.
Given a positive integer array nums and an integer k, return the number of non-empty subarrays of nums whose score is strictly less than k.
A subarray is a contiguous sequence of elements within an array.